检验在有理数中的应用

□赵国瑞

检验在有理数中的应用

□赵国瑞

数学中的检验并不仅限于解方程，很多问题都要用到检验.通过检验，不仅可以帮助我们判断原解答正确与否，还可以找出原题的正确答案.下面举例说明检验在有理数中的应用.

一、利用绝对值的非负性检验

例1若a＜0，则|2a|=_____.

错解：一些同学看到绝对值符号内的2a前面的正号省略，就误认为2a是正数，填“2a”.

检验：由于a＜0，即a是负数.根据有理数乘法法则知2a是负数.由于任意有理数的绝对值都是非负数，显然|2a|=2a错误.根据一个负数的绝对值是它的相反数，于是|2a|=-2a，故填“-2a”.

二、利用“互为相反数的两个数相加得0”检验

例2 a+b的相反数是_____.

错解：填“a-b”.

检验：根据有理数加法法则知，互为相反数的两个数相加得0，而（a+b）+（a-b）=2a，由于a为任意有理数，所以2a也为任意有理数，不一定等于0.因此a+b的相反数是a-b错误.所以a+b的相反数是-（a+b）.

三、利用近似数的概念进行检验

例3 8607000保留三个有效数字的近似数是______.

错解：8607000的第三个有效数字是从左边数起的第一个0，0后面是7，四舍五入应该向前进一位，0变成1，因此8607000保留三个有效数字的近似数是861.

检验：由“近似数”这个信息可知，8607000保留三个有效数字的值应与8607000近似相等，而8607000几乎是861的10000倍，显然结果错误.所以应该将861乘以10000，这样才与原数近似相等，然后再用科学记数法表示即为8.61×106.

四、利用“负数的奇次幂是负数，负数的偶次幂是正数”检验

例4计算：（-2）4.

错解：（-2）4=（-2）×4=-8.

检验：根据“负数的偶次幂是正数”可知（-2）4的结果一定是正数，因此（-2）4=-8错误.根据乘方的意义，得（-2）4=（-2）×（-2）×（-2）×（-2）=16.

五、利用特殊值进行检验

例5如图，用围棋子按下面的规律摆图形，则摆第n个图形需要围棋子的枚数是（）.

A.5n B.5n-1

C.6n-1 D.2n2+1

错解：选A.

检验：通过观察图形发现，摆第2个图形需要围棋子11枚.4个选项中，只有C选项符合“摆第2个图形需要围棋子11枚”，故应选C.

六、利用不同的计算方式检验

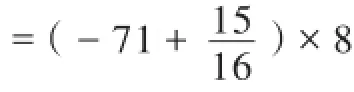
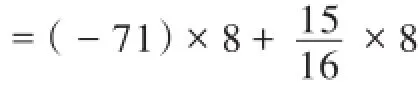
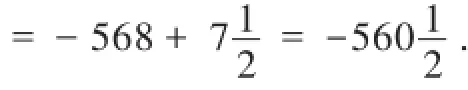
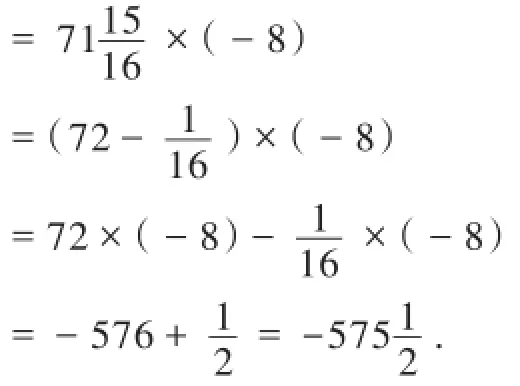
七、利用问题的实际意义检验

例7出租车司机小李某天下午在东西走向的一条街道上营运.如果规定向东为正，向西为负，他这天下午行车里程如下（单位：千米）：

+16，-18，-3，+15，-11，+14，+10，+4，-12，-15.

若汽车耗油为a升/千米，则这天下午汽车共耗油______升.

错解：汽车共耗油

［（+16）+（-18）+（-3）+（+15）+（-11）+（+14）+（+10）+（+4）+（-12）+（-15）］×a=0（升）.

检验：汽车行驶一个下午，不可能没有耗油，也就是说汽车耗油不可能等于0升.实际上在计算汽车耗油时，应该用汽车行驶的总路程乘以a，而上面在求汽车行驶的总路程时，将汽车行车里程中的数的符号也带上了，而符号只表示汽车行驶的方向，无论是向东还是向西每行驶1千米都要耗油a升，因此正确的计算过程如下：（16+18+3+ 15+11+14+10+4+12+15）× a=118a（升）.

当然，有理数中的检验还不止这些，希望同学们在平时的学习中注意归纳总结，做一个有心人.