小数轴大作用

□李庆社

小数轴大作用

□李庆社

数轴是数学中建立数与形密切联系的一座“桥梁”.数轴的应用比较广泛，借助数轴，可以解决有理数中的一些问题.

一、求有理数的值

例1已知数轴上有两点A，B，它们分别表示互为相反数的两个数a，b（其中a＞b），并且A，B两点间的距离是8，求a，b两数.

分析：根据互为相反数的几何意义，得出A，B两点在数轴上的位置.再根据“数轴上的点所表示的数，右边的总比左边的大”，正确解决问题.

解：根据相反数的定义可知，因为A，B互为相反数，所以A，B到原点的距离相等，又因为它们之间的距离是8，所以A，B距原点的距离都是4.因为a＞b，所以A点在原点右侧距原点4个单位处，B点在原点左侧距原点4个单位处，所以a=4，b=-4.

点评：若此题没有指明条件是a＞b，则要分两种情况进行讨论，即a＞b或a＜b时，分别求出a，b的值.

二、比较大小

例2有理数a，b，c的位置如图1所示，试确定下列各组数之间的大小关系.

图1

（1）a与b；（2）-a与-b；

（3）-b与c；（4）-a与c；

（5）a与-c；（6）b与-c.

分析：把a，b，c的相反数在数轴上表示出来，根据“在数轴上表示的两个数，右边的数总是比左边的大”，我们就可以比较出以上各组数的大小.

解：把-a，-b，-c在数轴上表示出来，如图2所示，

图2

由图可知：

（1）a＜b；（2）-a＞-b；

（3）-b＜c；（4）-a＞c；

（5）a＜-c；（6）b＞-c.

例3有理数a，b满足a＞0，b＜0且|a|＜|b|，用“＞”将a，b，-a，-b排列起来.

分析：要比较a，b，-a，-b的大小，可以在数轴上找到表示这4个数的点的位置.因为|a|＜|b|，故表示数a的点到原点的距离比表示数b的点到原点的距离要近，再根据“互为相反数的两个数在原点两侧，并且到原点的距离相等”这一性质，在数轴上找出表示a，b，-a，-b的位置，即可知它们的大小.

解：将a，b，-a，-b在数轴上的位置表示出来，如图3所示，由图可知-b＞a＞-a＞b.

图3

点评：借助数轴，运用数形结合思想，可使问题化难为易.

三、判断符号

例4有理数a，b在数轴上的位置如图4所示，则在a+b，b-2a，|b|-|a|，|a-b|，-|a+2|，b-2中负数共有______个.

图4

分析：本题为填空题，但直接推理较复杂，可以结合数轴信息，采用特殊值法来解决.

解：由于a在-2和-1之间，b在0和1之间，而a，b分别取各自区间的任何数都不会改变上述各式的符号.不妨设，分别代入上面各式，即得a+b=-1＜0，，故上面各式中负数共有4个.

四、化简求值

例5 a，b在数轴上对应的数如图5所示，化简|a-b|-|a|+|b|+|a+b|.

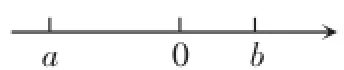
图5

分析：本题可以直接观察数轴来得到所需要的信息.

解：观察数轴可知：a＜0，b＞0，|a|＞|b|.

∴a-b＜0，a+b＜0.

∴|a-b|=b-a，

|a+b|=-（a+b）.

∴原式=b-a+a+b-ab=b-a.

例6有理数a，b，c在数轴上的位置如图6所示，试化简|a+c|-|a+b+c|-|b-a|+|b+c|.

图6

分析：结合数轴先判定a+c，a+b+c，b-a，b+c的正负，然后去绝对值符号、合并.

解：观察数轴知a+c＜0，a+ b+c＜0，b-a＜0，b+c＜0.

则原式=-（a+c）+（a+b+ c）+（b-a）-（b+c）

=-a-c+a+b+c+b-a-b-c

=-a+b-c.

点评：化简含绝对值的代数式，首先应结合数轴，判断出绝对值内代数式的正负，再去掉绝对值符号，最后合并同类项.

五、求距离

例7一跳蚤在一直线上从O点开始，第1次向右跳1个单位，紧接着第2次向左跳2个单位，第3次向右跳3个单位，第4次向左跳4个单位，依此规律跳下去，当它跳第100次落下时，落点处离O点的距离是_______个单位.

分析：将跳蚤跳动的次数与位置借助数轴来表示即可解决问题.

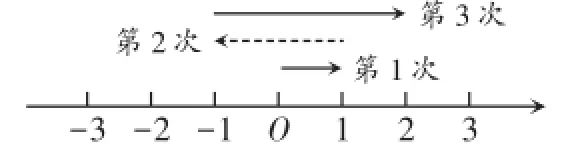
图7

解：将跳蚤跳动的次数与位置借助数轴来表示，原点向右为正方向，第1次向右跳1个单位，其位置表示的点为1；紧接着第2次向左跳2个单位，其位置表示的点为-1；第3次向右跳3个单位，其位置表示的点为2；第4次向左跳4个单位，其位置表示的点为-2，依此规律跳下去，第n（n≥1）次落地时，其位置表示的点为，故第100次跳后落下，其位置表示的点为-50，故此时落点处离O点的距离是50个单位.

点评：借助数轴，能发现跳蚤落点的规律，可巧妙地求出跳蚤跳第n次落地时，落点处离O点的距离.