折射和半波损失情况下布拉格方程的推导
张 超,胡建民, 黄晓利,王月媛,王选章
(哈尔滨师范大学 光电带隙材料省部共建教育部重点实验室 物理与电子工程学院,哈尔滨 150025)
折射和半波损失情况下布拉格方程的推导
张超,胡建民, 黄晓利,王月媛,王选章
(哈尔滨师范大学 光电带隙材料省部共建教育部重点实验室 物理与电子工程学院,哈尔滨150025)
为简化布拉格方程的推导过程同时又能深刻反映晶体X射线衍射的物理本质,本文在考虑折射和半波损失的情况下,在单光束反射模型的基础上根据折射定律和相干条件给出布拉格方程的推导过程,得到更具有普遍意义的布拉格方程.
晶体折射;半波损失;布拉格方程
X射线被发现以后,德国物理学家劳厄将晶体看作三维衍射光栅,既证明了X射线的电磁波本质,又证实了晶体结构的周期性,由此建立晶体X射线衍射方程[1].1913年,布拉格父子提出晶面反射模型,推导出布拉格方程.林一山根据光的衍射理论对布拉格条件做了定量推导[2].现有教材和文献大多采用的晶面反射模型如图1所示,晶面间距为d,反射X光的光程差为波长λ的整数倍时发生衍射加强,于是得出2dsinθ=mλ,其中θ为衍射角,m为衍射级数.图1所示的晶面反射模型是两条或两条以上的入射光束经过不同晶面反射后发生的相干叠加,在此称为多光束反射模型.姚忠祥在考虑晶体折射率n的情况下对布拉格方程进行修正,由此得到的布拉格方程为[3]
(1)
显然,方程(1)没有考虑X射线在晶体界面上的相位问题,即半波损失.半波损失是指当光束由折射率较小的介质经过界面进入折射率较大的介质时,其电矢量方向发生改变,即振动相位发生突变[4].为使几何光程和相位一致,需要在几何光程的基础上考虑半波损失.
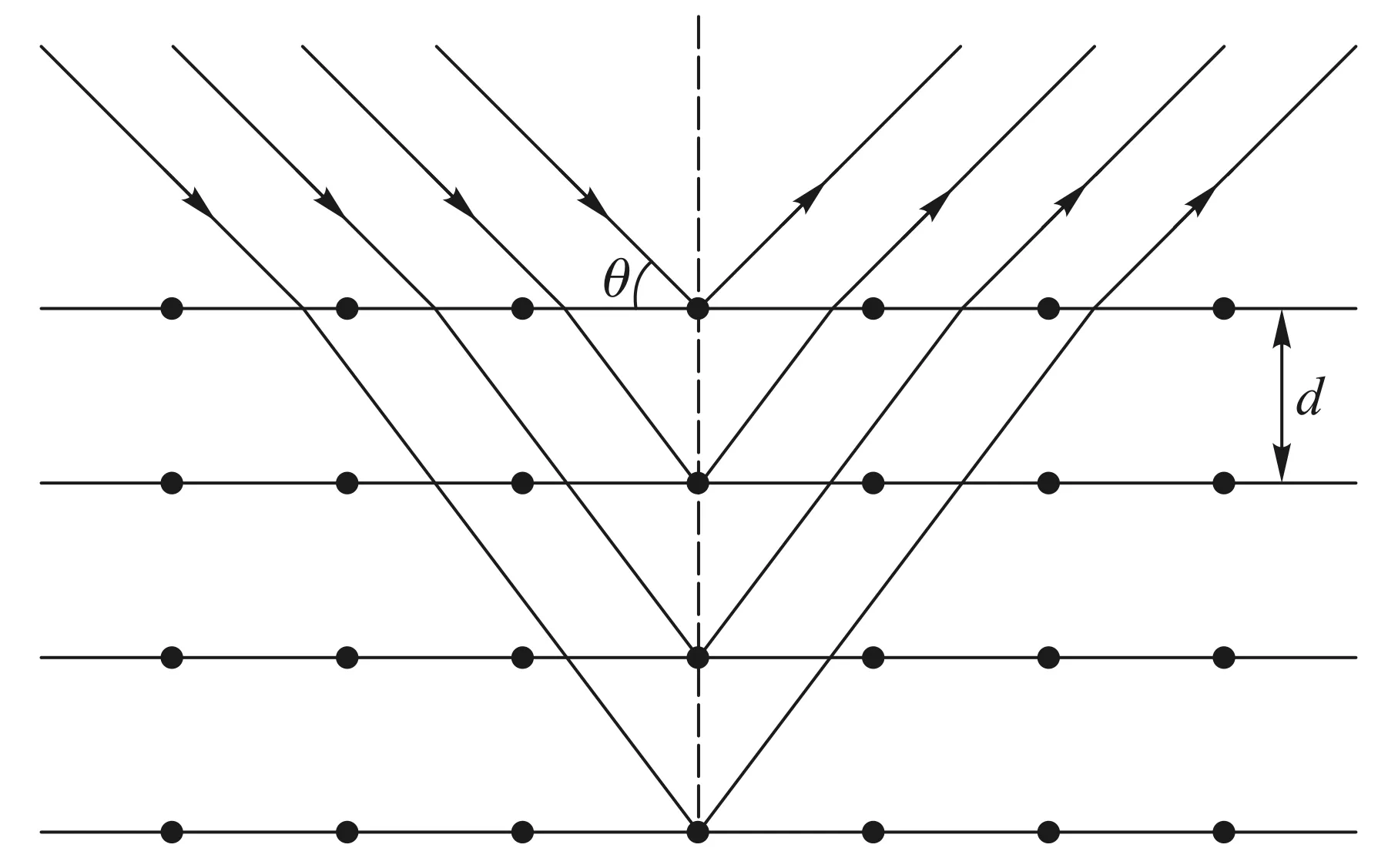
图1 特定情况下的多光束反射模型[3]
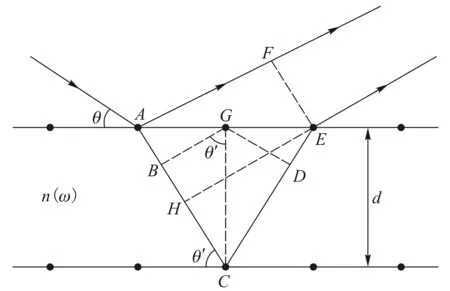
图2 单光束反射模型
如果只取一束X射线被不同的晶面反射,在反射光的光程差满足波长整数倍条件时也可以发生相干叠加,在此称之为单光束反射模型,如图2所示.由于X射线衍射的物理本质是晶体中所有原子经典散射波相干叠加的结果.所以,采用单光束反射模型推导布拉格方程即可以简化推导过程又能够深刻反映晶体X射线的物理本质.本文在考虑折射和半波损失的情况采用单光束反射模型给出布拉格方程的推导过程.

(2)
根据折射率的定义
cosθ=n(ω)cosθ′
(3)

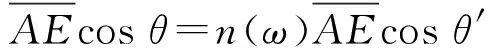

(4)
又

(5)
由式(2)﹑式(4)和式(5)可得
(6)
当光程差等于入射光波长的整数倍时发生相干叠加
(7)
这就是考虑折射和半波损失情况下采用单光束反射模型推导的布拉格方程.在不考虑半波损失的情况下式(7)与式(1)一致.由式(7)可见,当衍射角发生变化时,对于面间距不同的晶面将对应不同的衍射峰,而半波损失并不影响衍射谱的基本特征(衍射峰的形状和相对位置),所以X射线衍射在实际应用中并不考虑半波损失.此外,X射线衍射在本质上是晶体中所有原子经典散射波相干叠加的结果,而折射和半波损失只发生在晶体表面,对于晶体内部的晶面不会发生折射和半波损失.理想情况下,晶体表面原子数远远小于晶体内部原子数,这也是晶体结构的X射线衍射分析中不考虑折射和半波损失的一个重要原因.
[1]胡建民,周胜,信江波,等. 固体物理学教程[M]. 哈尔滨:东北林业大学出版社,2010:46-51.
[2]林一山. 对布拉格条件的严格推导[J]. 大学物理,2009,28(8):56-58.
[3]姚仲祥. 折射和色散对布喇格方程的影响[J]. 长春光学精密机械学院学报. 1989,12(3):83-86.
[4]Born M,Wolf E.光学原理[M]. 北京:电子工业出版社,2005:35-36.
Derivation of the Bragg equation in the case of refraction and the half-wave loss
ZHANG Chao, HU Jian-min, HUANG Xiao-li, WANG Yue-yuan,WANG Xuan-zhang
(Key Laboratory for Photonic and Electronic Bandgap Materials, Ministry of Education, School of Physics and Electronic Engineering, Harbin Normal University, Harbin, Heilongjiang 150025, China)
To simplify the derivation of the Bragg equation and at the same time to reflect profoundly the physical nature of the crystal X-ray diffraction, a more universal Bragg equation is given using the single-beam reflectance model on the basis of law of refraction and coherent conditions in the case of considering refraction and the half-wave loss.
crystal refraction; half-wave loss; Bragg equation
2015-02-11;
2015-06-02
黑龙江省高等学校教改工程项目(JG2013010361)和国家自然科学基金项目(11075043)资助
张超,(1989—),男,甘肃武威市人,哈尔滨师范大学物理与电子工程学院2010级本科生.
胡建民,Email:hujianmin@foxmail.com
O 436.1;
A
1000- 0712(2016)01- 0057- 02

