带状线内TEM波的场分布及其结构仿真
王福谦
(长治学院 电子信息与物理系,山西 长治 046011)
带状线内TEM波的场分布及其结构仿真
王福谦
(长治学院 电子信息与物理系,山西 长治046011)
通过求解拉普拉斯方程,给出带状线内TEM波场分布的级数解,并利用软件MATLAB和HFSS对其进行数值模拟和结构仿真.研究结论对于计算该传输线的衰减常数、了解其功率容量、考虑功率耦合及设计有关的有源器件具有一定的参考价值.
带状线;拉普拉斯方程;TEM波;MATLAB;HFSS;结构仿真
为了传输微波功率,人们提出并实现了各种结构形式的传输线,例如,带状传输线(一种平面传输线),它非常适合于微波集成电路和光刻加工制造.目前文献[1-3]中多报道有关带状线特性阻抗的计算,而对其内部TEM波的场结构的研究还未见涉及.然而,场结构在工程上具有重要性,为了了解传输线的功率容量、计算其衰减常数、考虑功率耦合及设计有关的有源器件等,需要讨论各种传输线的电磁场结构.为此,本文在引用文献[4]相关结论的基础上,拟利用其拉普拉斯方程的级数解来研究带状线内TEM波的场分布,并利用软件MATLAB和HFSS对其进行数值模拟和结构仿真.
1 带状线内静电场的近似解

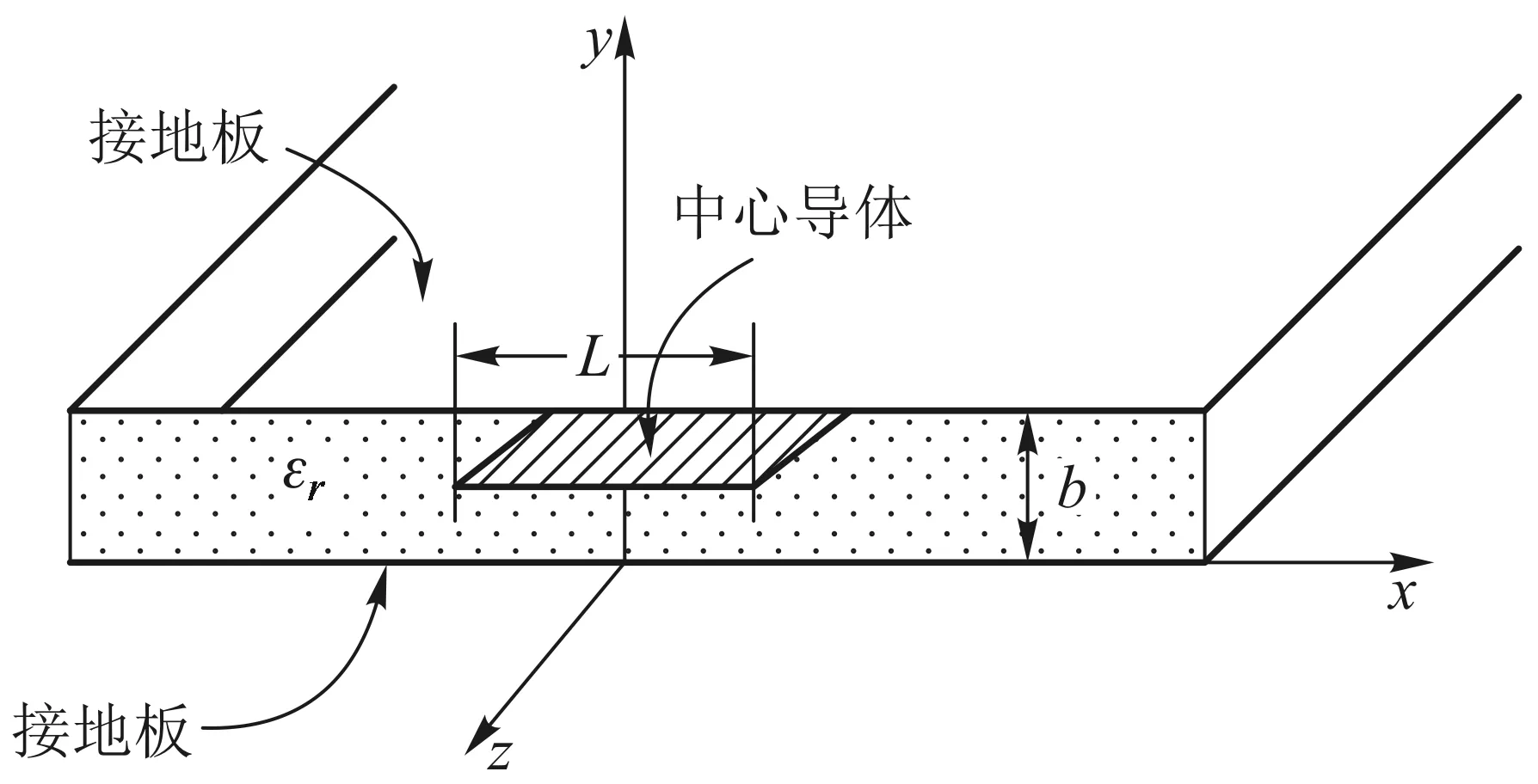
图1 带状线的几何结构图

图2 封闭带状线的横截面
(1)
边界条件为
φ(x,y)=0,在x=±a/2处
(2)
φ(x,y)=0,在y=0,b处
(3)
考虑到位于y=b/2处的中心导体上存在电荷密度,φ在y=b/2处不连续,故对两个区域的电势φ(x,y)分别求解,其通解为[4]
(4)

An=Bn
而An可通过求解中心导体带上的电荷密度得到.因为Ey=-∂φ/∂y,故
(5)
在y=b/2处的带上的电荷面密度为
ρs=Dy(x,y=b/2+)-Dy(x,y=b/2-)=
(6)
由式(6)可知,中心导体表面电荷密度ρs是x的傅里叶级数,若得知ρs,则可得到系数An的表达式.假定电荷是近似均匀地分布在导体带上的一常数ρ0,则有
(7)
令式(7)与式(6)相等,并利用cos(nπx/a)函数的正交性,得
(8)
由式(4)可得带状线内静态场电场的x分量为
(9)
综合式(5)和式(9),可得带状线内静电场分布为:

(0≤y≤b/2)
(10)
(11)
式 (10)、式(11)为在静态场情形下的带状线内部的场强分布表达式.式中ex、ey为该传输线横截面上沿x、y方向的单位矢.
2 带状线内TEM波的解析解
带状线内TEM波的求解,可由静态场在相同边界条件下的解,得到其电场在此传输线横截面上的分布,乘以波动因子e-jβz得到电场的解,再由麦克斯韦方程组所给出的电、磁场关系得到其磁场的解[5].则带状线中的TEM波的场强分布为:
(0≤y≤b/2)
(12)
(13)

TEM波的电场与磁场是由麦克斯韦方程组相互联系的,它们相互激发,不可分割,满足如下规律[5]:
ET=ηHT×ez
(14)
(15)

又由式(15)及式(12)、式(13),得:
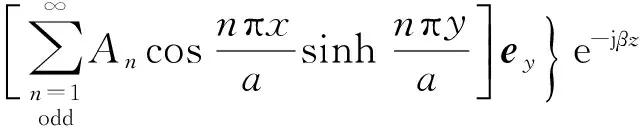
(0≤y≤b/2)
(16)
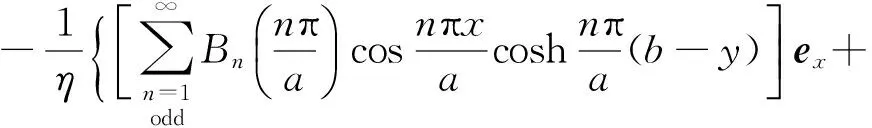
(b/2≤y≤b)
(17)
式(12)、式(13)及式(16)、式(17)即为带状线中的TEM波的解析解.此4个式子给出了带状线中TEM波的场结构.
3 场结构的数值模拟与结构仿真
为了给出带状线中TEM波的场结构的直观图像,并进一步验证本文所得结论的正确性,下面利用软件MATLAB和HFSS对其进行数值模拟和结构仿真.
图3为利用数学软件MATLAB所绘制出的带状线横截面上TEM波场结构图.从该图可以看出,带状线内的TEM波在此传输线横截面上呈对称分布,作出的图与预期结果(电场线与磁感线及导体表面均垂直)相符.图4为由HFSS软件仿真的带状线横截面上某一时刻TEM波的场结构图,将其场线分布与图3比较可以看出,MATLAB软件的数值模拟结果,与HFSS软件的结构仿真结果一致,这说明本文中研究带状线内TEM波场结构的方法正确,结论可靠.
图5和图6为通过HFSS软件仿真出的带状线内TEM波的三维电磁场结构图,场分布形象直观,便于对场结构的整体把握,供考虑功率耦合及设计有源器件时,在传输线上选取恰当位置,以实现该传输线与其他电磁结构之间的能量耦合及接入有源器件时使用和参考.
由图3至图6可见,在带状线内部,愈靠近内导体表面,电磁场愈强.因此,内导体的表面电流密度较外导体内表面的表面电流密度大.所以带状线的热损耗主要发生在截面尺寸较小的内导体上.

图3 带状线横截面上TEM波的场结构图(由MATLAB软件模拟)

图4 带状线横截面上TEM波的场结构图(由HFSS软件仿真)
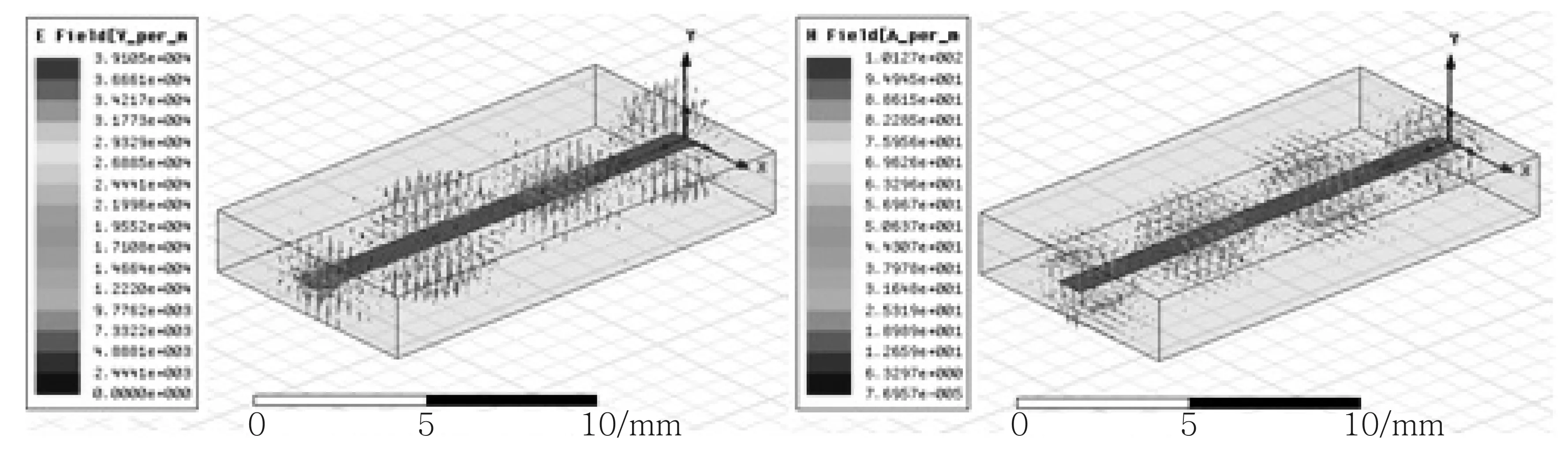
图5 带状线内TEM波的场结构图(由软件HFSS仿真,Field Overlays;Vector-E、Vector-H)
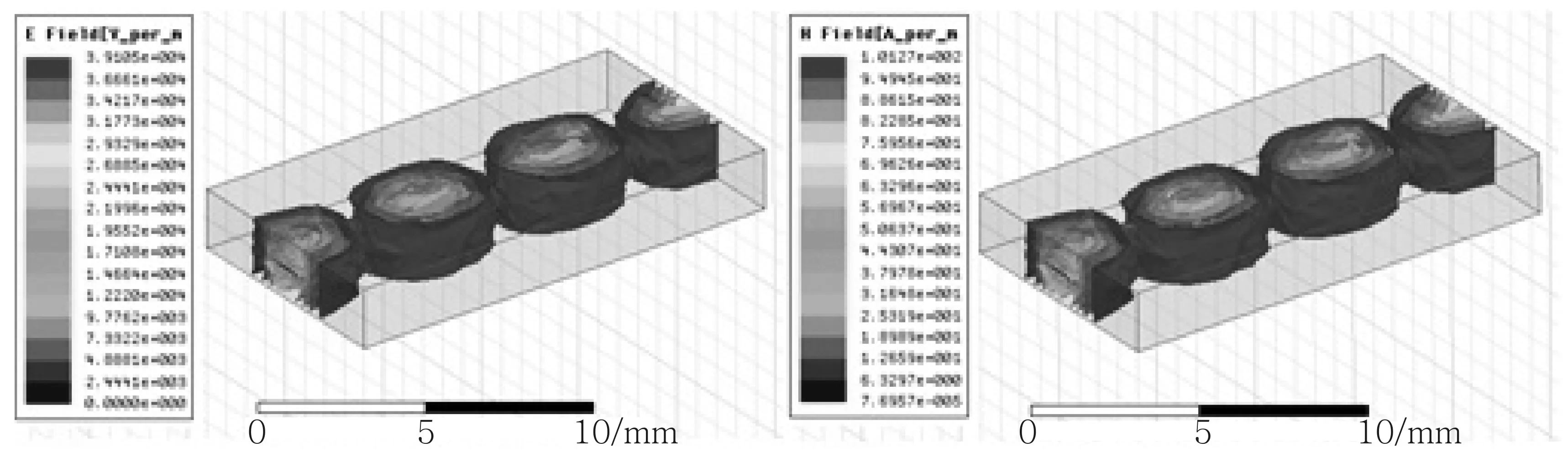
图6 带状线内TEM波的场结构图(由软件HFSS仿真,Field Overlays:Mag-E、Mag-H)
4 结束语
本文对带状线内TEM波场结构的研究,解决了该传输线的计算问题,给出了该传输线内电磁场的分布规律.由于传输线内TEM波的场分布,对于了解传输线的功率容量、计算衰减常数、考虑功率耦合及设计有关的有源器件等都是不可缺少的,故所得结论具有一定的理论价值和实际意义.
[1]宋斌,傅君眉.采用边界元法求解带状传输线的特性阻抗[J].无线电工程,1991,22 (1):51-55.
[2]吴忠贤.有限差分法求带状线的特性阻抗[J].电工教学,1991,14 (4):48-56.
[3]吴富根.带状线(微带线)及其传输特性[J].光纤与电缆及其应用技术,1992(1):37-43,62.
[4]David M Pozer.微波工程[M].3版.张肇仪,等,译.北京:电子工业出版社,2006.
[5]沈熙宁.电磁场与电磁波[M].北京:科学出版社,2006:375-381.
The field distribution of TEM wave in a strip line and its structure simulation
WANG Fu-qian
(Department of Electronic Information and Physics,Changzhi University,Changzhi,Shanxi 046011,China)
By solving Laplace’s equation,the series solution of the field distribution of the TEM wave in a strip line is obtained.Further,the TEM wave in a strip line is simulated by MATLAB and HFSS.The present study has the certain reference value for calculating the decay constant of the transmission line,realizing its power capability,considering its power coupling and designing the related active device.
strip line;Laplace’s equation;TEM wave;MATLAB;HFSS;structure simulation
2015-02-02;
2015-07-22
山西省自然科学基金(2012011028-1)资助
王福谦(1957—),男,山西临猗县人,长治学院电子信息与物理系教授.主要从事电磁场边值问题及场结构数值模拟研究.
TN 011
A
1000- 0712(2016)01- 0024- 04

