单摆的超大振幅振动
王成会,莫润阳,边小兵
(陕西师范大学 物理学与信息技术学院,陕西 西安 710062)
单摆的超大振幅振动
王成会,莫润阳,边小兵
(陕西师范大学 物理学与信息技术学院,陕西 西安710062)
基于单摆的动力学方程和运动初始条件对单摆的大振幅振动进行了近似分析,介绍了一种估计摆振幅接近π的振动周期的解析方法. 结果表明,当摆振幅小于2.8rad时估计值偏离精确值较多,产生误差的原因在于采用了线性近似.
单摆;大振幅振动;周期
在给定竖直面内运动的单摆作为一种简单的物理模型[1],对学生认识振动现象具有重要的意义. 首先,摆的运动现象在现实生活中很常见,如秋千、钟摆等. 学生熟悉摆的运动情景,从摆的运动入手构建振动物理模型有利于学生认识从生活到科学的抽象过程和方法,可帮助学生构建科学思维. 正因为如此,目前仍然有许多从事物理教学和科研的同行们不断深入分析摆的运动特征[2-7]. 实际生活中地面上摆的运动受到很多因素的影响,如地球自转、地球公转、空气阻力、悬线弹性形变等,可是当将摆的运动转化成物理问题时,通常忽略这些因素的影响,将生活中的摆抽象成“理想摆(单摆)”,即由一根长度变化以及质量可忽略不计的长为l的细线(或轻杆)悬挂质量为m的摆球(质点)的运动,只考虑摆球受到悬线(或轻杆)拉力和重力作用的情形,此时摆球将在特定的竖直面内沿圆弧运动. 单摆的无阻尼振动的动力学方程为[1,2]
(1)

忽略单摆振动过程中阻力的影响,系统机械能守恒. 若选取单摆平衡位置为重力势能零点,则有
(2)

(3)
该式为一椭圆积分[2],直接计算通常比较困难,需要借助数学软件通过数值积分实现. 为方便人们估计单摆在大振幅振动时的周期,需要对式(1)和式(2)做近似分析,如将sinθ作泰勒展开保留角位移θ的高阶项,利用逐级近似法可在一定精度上估计单摆振幅在(0,π/2)之间做大振幅振动时的周期变化[8,9]. 谭志中等利用局部常化三倍角公式给出近似估计单摆振动周期的修正方法[10],并将结果同其他近似方法估计结果进行了比较. 然而,当振幅大于π/2时,前面的方法将不再适用.为此,我们需要发展更好的估计振幅大于π/2的摆周期的方法,而本文将介绍一种分析振幅θ0接近π时的单摆的运动和振动周期的方法.
当单摆振幅θ0无限趋近于π时,sin(θ0/2)≈1,故有
(4)
即为单摆运动角速度和角位移之间的关系. 当t=0,单摆经过平衡位置,则有θ=0,对式(4)取正号在初始条件t=0,θ=0下积分[2],有
θ(t)≈π-4arctan(e-ω0t)
(5)
此式表明,当t→-∞时,摆球角位移-π,而t→∞时,摆球角位移π. 从数学分析看,当单摆振幅无限趋近于π时,周期似乎是无穷大.然而,数值结果告诉我们,当ω0t=9时,arctan(e-ω0t)≈0.0001,随着ω0t增加,arctan(e-ω0t)趋近于零,θ(t)无限趋近于π. 将式(4)对时间t求导,得
(6)
当t=0时,单摆处在平衡位置,其角速度为2ω0,当ω0t=π,即t=T0/2时,角速度约为0.17ω0,而当ω0t=2π,即t=T0时,角速度约为0.0075ω0,可见角速度在T0/2时间间隔(从T0/2变化到T0)内,角速度减小了约22/23,而角位移变化仅为0.17rad. 由此可见,当单摆做振幅趋近于π的大振幅振动时,单摆在从平衡位置向正最大角位移运动的过程中,在此过程后期的运动非常缓慢,故其周期为有限值,我们可借助于图像分析技术研究角位移式(5)或角速度式(6)随时间变化的趋势,在一定精度范围内估计单摆振幅无限趋近于π时的振动周期. 除图像分析技术外,基于式(5)或式(6),本文将介绍一种很好的解析方法分析摆作振幅超过π/2的振动时的运动行为和周期.
图1给出了单摆振幅分别为3.1和3.0的振动相图,如实a和虚线b所示. 比较曲线a和b发现当角位移|θ|<θC时两曲线几乎重合,此处θC为两曲线重合区域角位移绝对值的最大值. 这表明当单摆作振幅趋近于π的大振幅振动时振幅变化对其振动周期的影响主要发生在角位移|θ|≥θC的范围之内.
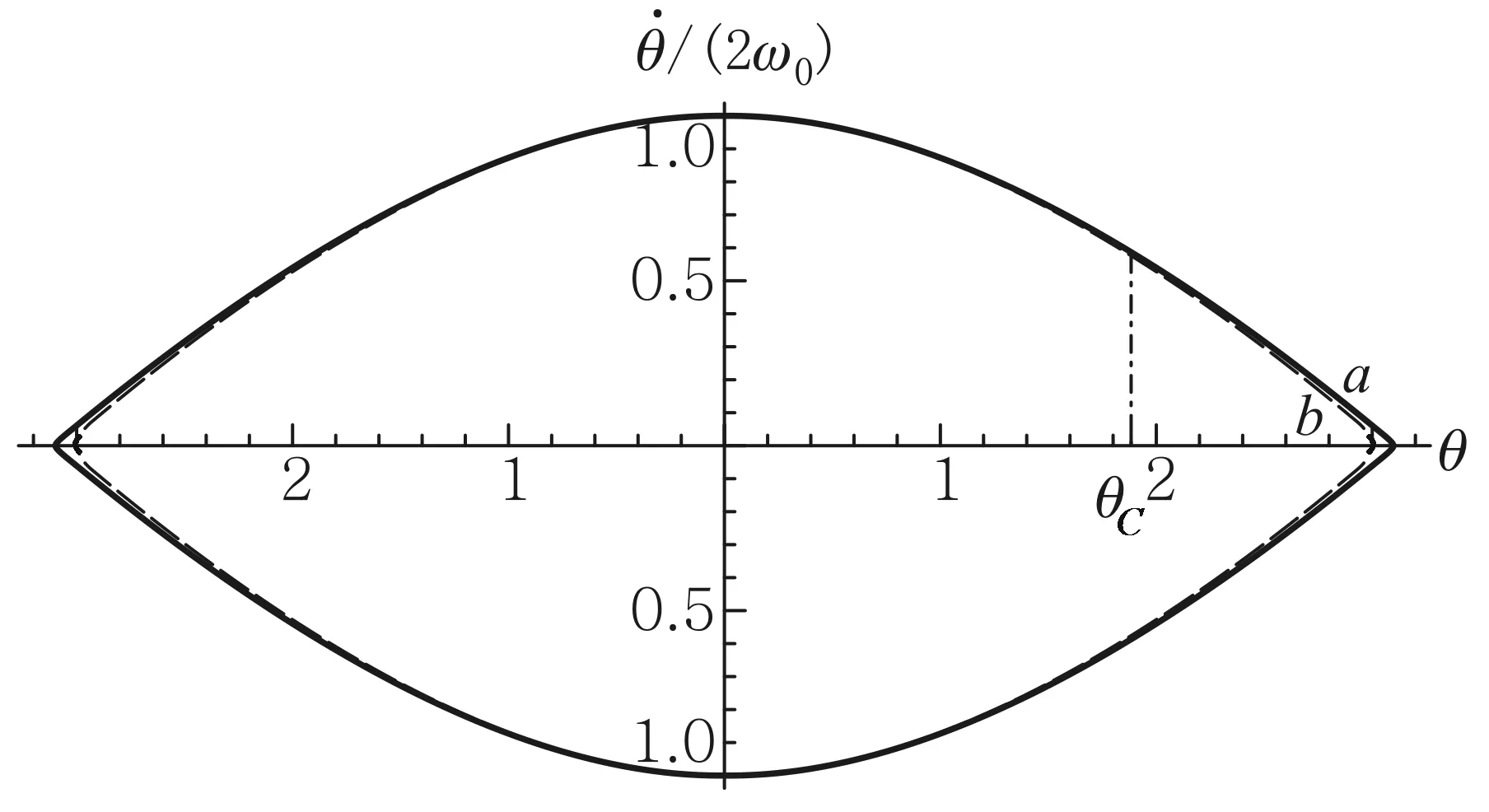
图1 单摆大振幅振动的相轨迹曲线a:θ0=3.1, 曲线b: θ0=3.0

(7)
当θ20≈π时,近似有
(7a)

(8)
根据无阻尼摆振动的对称性知,若能估计单摆从θC变化至θ10所用时间t2,则此时单摆周期为T=4(t2+t1). 设α=π-θ,当有α<<1时,代入式(1),有[2]
(9)

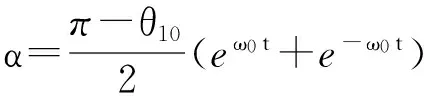
(10)
(11)

(12)
故
(13)
利用角速度变化关系,结合式(6)和式(11)可同样得到式(13)给出的周期表达式. 从式(10)和式(11)可以看出,在一级近似条件下,单摆在其振动正负最大位移附近角位移和角速度随时间成指数增加或减小,但π-θ10越小,形成较大角位移变化所耗时间就越长,因此θ10越大,单摆的周期越长.
图2给出了分别用式(3)和式(13)计算得到的单摆大振幅振动周期变化趋势图.周期计算式(3)为一椭圆积分,由于在推导过程中没有引入任何近似处理,故本文将式(3)数值积分后得到的周期值作为精确值和近似计算式(13)进行比较.图2中符号‘◆’代表由式(3)得到的周期值,曲线代表式(13)计算得到周期值.结果表明,若单摆振幅大于2.8rad,可用式(13)在一定精度范围内估算单摆大振幅振动周期. 可是,当单摆振幅小于2.8rad时,式(13)估算得到的单摆大振幅振动期小于式(3)计算所得周期,估计值偏小包含两个方面的原因:1) 随着θ10减小,cos(θ10/2)增大,因此采用式(8)估计得到的t1值偏小;2) 随着θ10减小,α增大,此时sinα≈α-α3/6,代入式(1),可得
(14)
利用逐级近似法,设α=α1+α2,有一级近似解为α1=(π-θ10)coshωt,式中ω=ω0+Δω,代入式(14),得二级近似解满足的方程为
(15)
上式coshωt系数为零,得

(16)
(17)
因此,当θ10减小时,近似有
(18)
式中k<1,故式(18)估算的t2值大于式(12)估算得到的t2值,即当θ10减小时,由线性近似得到的式(12)估计值t2偏小.
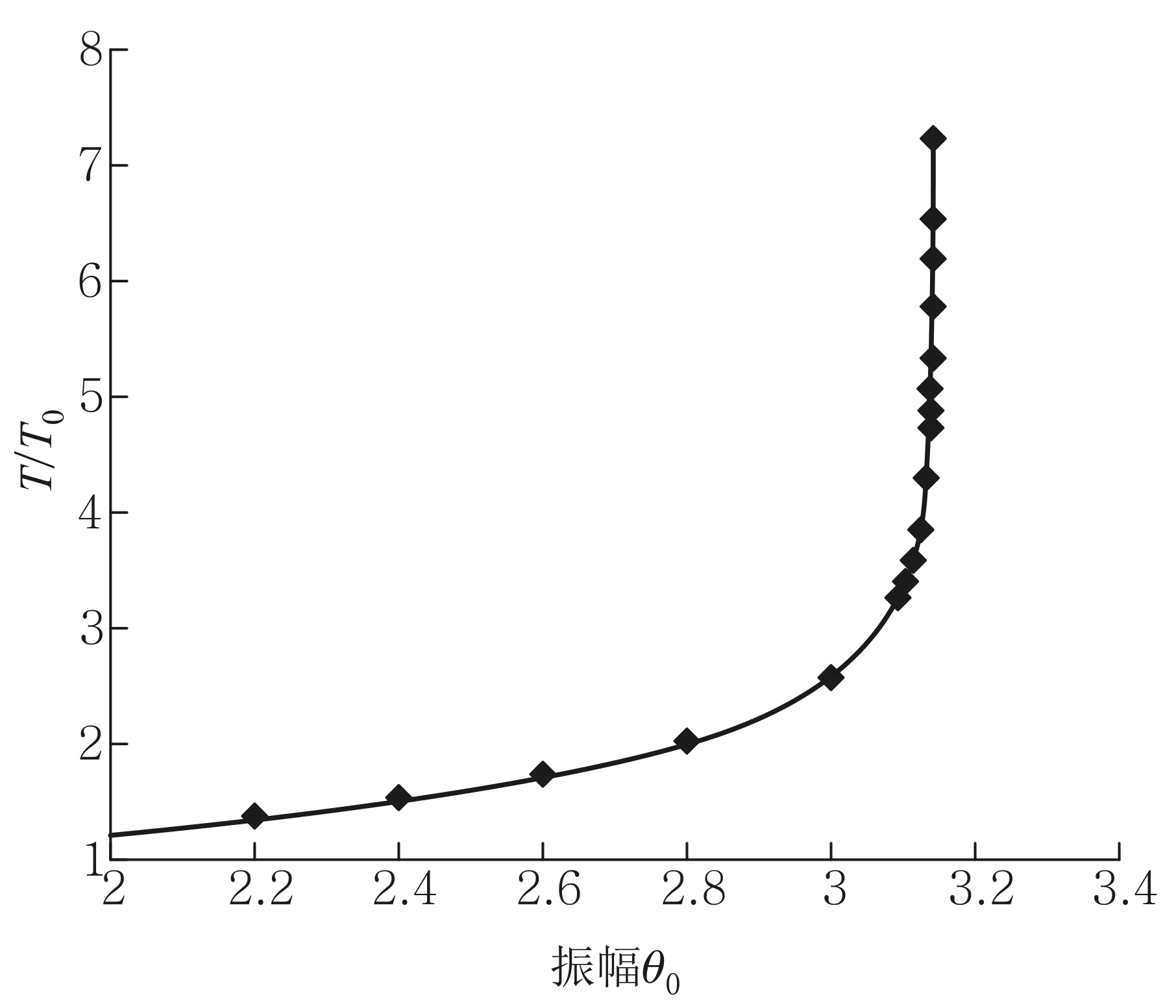
图2 单摆大振幅周期变化趋势图.
结论:本文对单摆做振幅大于π/2的振动做了近似分析,介绍了一种估计大振幅振动周期的方法,并对此方法的可靠性进行了理论分析.结果表明,本文给出的周期估算式(13)在单摆振幅大于2.8rad时给出振动周期值和式(3)给出的摆周期值相比,相差较小,且振幅越接近π,估计值越接近(3)式给出的摆周期值; 而当单摆振幅小于2.8rad时估计值小于(3)式给出的摆周期值,差别形成原因在于分析过程中采用了线性近似.
[1]漆安慎,杜婵英.力学[M].2版.北京:高等教育出版社,2005:283-327.
[2]EugeneIButikov.Oscillationofasimplependulumwithextremelylargeamplitudes[J].EurJPhys,2012,33(6): 1555-1563.
[3]JoseFlores,GuillermoSolovey,SalvadorGil.Variablemassoscillator[J].AmJPhys,71(7): 721-725.
[4]BorisKorsunsky.Awesomeoscillations[J].PhysTeach,2008,46: 260.
[5]JohnDGarrison.Onthesolutionoftheequationfordampedoscillation[J].AmJPhys,1974,42: 694.
[6]EduardoERodrigue,GabrielAGesnouin.Effectivemassofanoscillatingspring[J].PhysTeach,2007,45(2): 100-103.
[7]YavorKostov,RagibMorshed,BarbaraHoling,etal.Period-speedanalysisofapendulum[J].AmJPhys,2008,76(10): 956-962.
[8]陈文涛,龚善初. 单摆振动分析[J]. 湖南理工学院学报(自然科学版),2008,21(1): 66-70.
[9]龚善初. 利用线化和校正法求非线性单摆运动的周期[J]. 大学物理,2006,25(2): 16-18.
[10]谭志中,罗利进. 用局部常化三倍角公式研究单摆周期[J]. 大学物理,2007,26(11): 25-33.
Oscillationofasimplependulumwithextremelylargeamplitude
WANGCheng-hui,MORun-yang,BIANXiao-bin
(SchoolofPhysics&InformationTechnology,ShaanxiNormalUniversity,Xi’an,Shaanxi710062,China)
Basedonthedynamicalequationsandtheinitialconditions,theoscillationofasimplependulumwithlargeamplitudeisanalyzedapproximately.Amethodisintroducedtoestimatetheperiodofasimplependulumwithanextremelylargeamplitudewhosevalueisapproachingπ.Theresultsshowthatthedeviationbetweentheexactvalueandestimatedvalueoftheperiodincreaseswiththedecreaseoftheoscillationamplitude.Thelinearapproximationleadstotheincrementoftheerrors.
simplependulum;largeamplitudeoscillation;period
2015-05-26;
2015-08-05
陕西师范大学教学改革项目资助
王成会(1974—),女,重庆万州人,陕西师范大学物理学与信息技术学院副教授,博士,主要从事力学和理论力学教学研究工作,硕士生导师.
O313
A
1000- 0712(2016)01- 0011- 04

