比值法液体比热容测量方案设计
马红章,刘素美,张亚萍,王 龙,李书光
(中国石油大学 理学院,山东 青岛 266580)
比值法液体比热容测量方案设计
马红章,刘素美,张亚萍,王龙,李书光
(中国石油大学 理学院,山东 青岛266580)
在电热法测量液体比热容实验中,通常运用牛顿冷却定律进行系统散热的修正.基于对系统散热的计算和分析,本文提出通过两个不同的电加热过程的系统散热比值的方法来测量液体比热容.实验测试结果显示该测量方案可操作性强,精度高,适于在大学物理实验教学中普及和推广.
比热容;电热法;比值法;牛顿冷却定律
物质的比热容是热力学中一个非常重要的物理量,是单位质量的物质,温度升高(或降低)1 K(或1 ℃)时所吸收(或放出)的热量.目前测量物质比热容的方法有混合法、冷却法、物态变化法、电流量热法[1].进行比热容的实验测量应遵循两条原则:一是保持系统为孤立系统,即系统与外界没有热交换;二是只有当系统达到热平衡时,温度的测量才有意义.理想的绝热系统往往是很难实现的,只要有温差存在,总会发生系统与外界热交换的现象,而不管系统与外界的热交换是放热还是吸热,都会给测量结果带来系统误差[2,3].本文基于牛顿冷却定律,通过对电热法测量液体比热容实验过程中系统散热的分析,设计了通过两个不同的电热过程的系统散热比值来抵消系统散热的液体比热容的测量新方案.
1 实验原理
1.1电热法原理
电热法测量液体比热容的实验装置如图1所示.电阻丝R两端电压为U,通过的电流为I,通电时间为t,则电阻丝释放的热量Q为
Q=UIt
(1)
设被测液体质量为m,比热容为c,系统其他附件(内筒、搅拌器、电阻丝等)总质量为m0,比热容为c0,测量过程中系统与外界无热交换时有
(2)
其中T1和T2为被测液体的初温和末温[4-6].

图1 液体比热容测量装置
1.2散热修正常规方法

(3)

设t0时刻开始加热,液体温度与环境温度相同,均为θ,t1时刻液体上升到最高温度T′,则在这个过程中,由于系统与外界热交换引起的系统温度变化量ΔT可用下式计算:
(4)
则系统无散热情况下的终了温度为
T2=T′+ΔT
(5)
在实验过程中可假定环境温度θ不变,因此式(3)可变形为
(6)
式(6)积分后为
ln(T-θ)=-Kt+b
(7)
即由系统自然散热数据,对ln(T-θ)与t的线性拟合可得到散热系数K.
实验中一般需要测量液体升温和降温两个过程,由降温数据计算系统散热系数K,再修正升温过程中由于系统散热所造成的系统温度变化量ΔT,得到绝热状态下系统的终温,实现对液体比热容的测量.
1.3散热修正新方案
设以不同的加热功率W1和W2分别对初始温度接近的同一系统进行加热,设W1加热功率下系统温度T1(t)与时间t的关系用Y1(t)表示;W2加热功率下系统温度T2(t)与时间t的关系用Y2(t)表示.
如示意图2所示,在两个加热过程中,系统温度达到T1的时刻分别为t11和t21,系统温度达到T2的时刻分别为t12和t22.以系统温度由T1变化到T2的过程为研究对象,对于情形1和情形2,分别有下式成立:
W1(t12-t11)=(cm+c0m0)(T2-T1)+Q1
(8)
W2(t21-t22)=(cm+c0m0)(T2-T1)+Q2
(9)
式中,Q1和Q2为系统与外界热交换的热量.

图2 不同功率加热时系统温度随时间的变化
由牛顿冷却定律知,Q1和Q2可表示为
(10)
(11)
如果温度T1与T2较接近,则系统温度T(t)与时间t可用线性关系表示,则
(12)
令t12-t11=Δt1和t22-t21=Δt2,则被测液体的比热容c可表示为
(13)
2 实验测试
2.1实验装置与测试数据
实验选用如图1所示的液体比热容测量装置,对变压器油(比热容理论值约1.92 kJ·kg-1·K-1)进行测量,装置中的内筒、搅拌器和其他配件的总质量m0为0.0939 kg,比热容c0为387 J·kg-1·K-1,油的质量m为0.142 kg.
在室温θ=23.1 ℃的条件下,利用热功率W1=2.10 W和W2=3.40 W分别对同一系统加热,加热时间分别为990 S和540 S,使系统温度上升了约5 ℃,如图3所示.系统由26 ℃自然降温至25 ℃的测量数据,如图4所示.
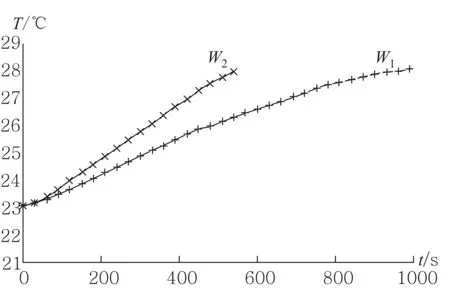
图3 不同功率加热下系统温度随时间的变化关系
2.2实验结果
2.2.1常规方法
由式(7),利用系统散热数据计算ln(T-θ),对ln(T-θ)与t进行线性拟合,如图5所示,得到K=0.000 349.

图4 系统散热数据
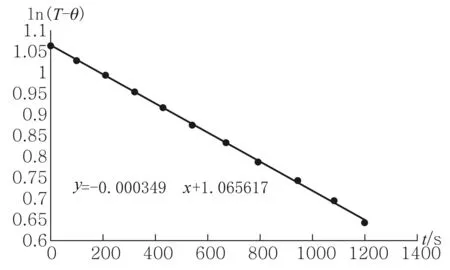
图5 ln(T-θ)与时间t的线性关系
由式(5),对两个过程做温度补偿,计算得到ΔT1=1.76 ℃,ΔT2=0.99 ℃,则系统在绝热状态下的理想终温分别为30.0 ℃和29.3 ℃,由式(2)直接计算油品的比热容分别为:c1=1866.0(J·kg-1·K-1),相对误差B=2.8%;c2=1829.5(J·kg-1·K-1),相对误差B=4.7%.
2.2.2新方法
采用最小二乘法分别对两个升温过程中24℃至27℃的温度与时间数据进行线性拟合,结果如图6所示.

图6 升温过程数据拟合
热功率W1=2.10 W情形,拟合结果为T=0.005906t+23.114;热功率W2=3.40 W情形,拟合结果为T=0.01t+22.8.利用拟合方程精确计算得到系统温度由T1=25 ℃升温至T2=26 ℃对应的加热时间为Δt1=169.4 s和Δt2=100.0 s,代入式(13)可得油品的比热容为c=1976.5 J·kg-1·K-1,相对误差B=2.9%.
3 讨论
本文提出的基于电热比值法对散热的处理取得了良好的效果,从实验结果看,新方案达到了相对误差小于3%;常规方法的测量结果相对误差在2%~5%的范围内,其中,采用低加热功率时测量结果精度较高.从数据处理和操作角度分析,新方案数据处理较为简单,克服了常规方法测量系统散热数据耗时较长的缺点.新测量方案为电热法测量液体比热容提供了一种简单、高效的测量备选方案,该方法适于在大学物理实验电热法测量液体比热容实验的教学中推广.
[1]阎向宏,张亚萍.电热法测液体比热容实验的改进[J].大学物理,1997,16(7):23-24.
[2]喻凌,潘学军.液体比热容的测量[J].四川师范大学学报(自然科学版),2003,26(3):306-308.
[3]储浚.电热法测液体比热实验中的散热修正[J].物理实验,1995,15(3):107-108.
[4]牛法富,孟军华,张亚萍.液体比热容测量散热修正新方法研究[J],大学物理实验,2011,24(3):54-56.
[5]孟军华,牛法富,张亚萍.新型液体比热容测量装置与方法的设计[J],实验室研究与探索,2011,30(4):14-16.
[6]刘志华,刘瑞金.牛顿冷却定律的冷却规律研究[J].山东理工大学学报:自然科学版,2005,19(6):23-27.
[7]李书光,张亚萍,朱海丰.大学物理实验[M].北京:科学出版社,2012.
[8]李相银.大学物理实验[M].北京:高等教育出版社,2004:133.
A method of electric heating ratio measuring the specific heat capacity of liquid
MA Hong-zhang,LIU Su-mei,ZHANG Ya-ping,WANG Long,LI Shu-guang
(College of Science,China University of Petroleum,Qingdao,Shandong 266580,China)
In the liquid specific heat capacity measurement experiment using the electric heating method,the Newton’s law of cooling is usually used to correct the system heat dissipation problem.Through calculation and analysis of the system heat dissipation,a new measurement scheme is put forward to reduce the effects of the system heat dissipation on the test results.The system heat dissipation ratio of two different heating processes is used to measure the liquid specific heat capacity in the new method.Test results show that the measurement scheme has strong operability and high precision,which is suitable for popularization and promotion in the university physics experiment teaching.
specific heat;electrothermal process;ratio method;Newton’s law of cooling
2015-03-01;
2015-07-12
中国石油大学教学改革重大项目(JYA201402)资助
马红章(1977—),男,河北衡水人,中国石油大学理学院讲师,主要从事大学物理实验教学与研究工作.
O 551.1
A
1000- 0712(2016)01- 0039- 03

