匀速运动介质中的声波干涉
吕令杰
(山东师范大学 物理与电子科学学院,山东 济南 250358)
匀速运动介质中的声波干涉
吕令杰
(山东师范大学 物理与电子科学学院,山东 济南250358)
探讨了由两个静止声源产生的声波在匀速运动的介质中的干涉,计算了两声源在同一时刻产生的两列等相位的波面分别到达某点的时间差,并与角频率相乘求得该点的相位差,进而得到了等相位差的点所满足的方程,最后讨论了几个特殊位置处的干涉情况及相关应用.
声波干涉;运动介质;相位差;纵波;测速
当介质相对声源匀速运动时,声波的波长在空间中有所改变,但只要观察者相对于声源静止,在声场中任意点观测到的声波频率都是相等的,并且等于声源振动的频率[1].基于此,本文认为两个静止的相干声源在匀速运动的介质中仍然会产生干涉. 笔者认为对于上述问题,一般情况下常以介质为参考系讨论声波的干涉,但是,若选择两相对静止的声源为参考系则便于问题的讨论.此时各质元的位移可以分解为质元因振动而偏离其平衡位置的位移(下文称振动位移)和平衡位置运动的位移.因为介质是整体运动的,即各质元平衡位置运动的位移是相等的,该位移分量不会改变相应质元平衡位置处的密度或压强.假如我们只关心某点处的密度或压强的变化情况,那么只需考虑平衡位置位于该点的质元的振动位移的变化.平衡位置位于该点的质元的振动位移的变化情况反映了该点的振动情况,其变化频率即该点的声波频率.与介质静止时不同,由于介质的运动,各质元的平衡位置依次经过该点,因此平衡位置位于该点的质元是时刻更替的,可见该点的声波频率同时取决于质元的振动频率和介质的运动速度.上述问题若选择两相对静止的声源为参考系,两声波在各点的频率是相等的,平衡位置位于某点的质元振动位移的矢量和反映了该点的干涉情况.
若两声源初相位相同,分别计算出两声源在同一时刻产生的两列波面到达某点的时刻t1、t2,两个时刻的差值Δt乘以角频率ω即得到该点的相位差,即
Δφ=ωΔt=2πf(t2-t1)
(1)
式中f为声源振动频率.
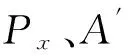

图1 计算相位差的示意图
(x+l-vxt1)2+(y-vyt1)2=(v0t1)2
(2)
取其正根
(3)
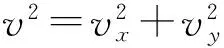
(x-l-vxt2)2+(y-vyt2)2=(v0t2)2
(4)
取其正根
(5)
将t1、t2代入式(1)得


(6)
令式(6)中v=0,有
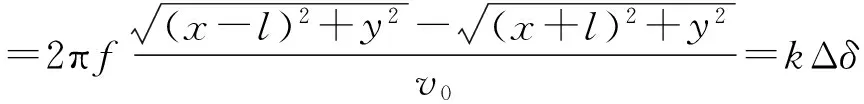
(7)

为了便于讨论,令Δφ=±nπ
(8)
n取不同的实数值对应不同的相位差.将式(8)代入式(6),整理得速度为v时等相位点满足的方程
(9)
当v=0时式(9)成为静止介质中等相位点满足的方程:
(10)
由双曲线的定义知,当n确定且n≠0时,该式是关于x和y的双曲线方程(n=0时为直线),双曲线的焦点为两声源的坐标(±l,0),不同的非零n对应不同的双曲线对.由于有轴对称性,等相差的点在空间中形成旋转双曲面.
当vx=0而vy≠0时,式(9)成为
(11)
(12)
令
(13)
上式写成
(14)
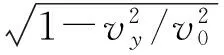

图2 式(14)的图像
当vx≠0而vy=0时,式(9)成为
(15)
等号两边同除以v0,得
(16)
令
(17)
则上式写成
(18)


图3 式 (18)的图像
当vx≠0而vy≠0时,式(9)不再是双曲线方程,但速度不太大时与双曲线非常接近.
下面讨论几个特殊位置处的干涉情况.
令式(6)中x=0,有

(19)
vy=0且vx≠0时,有
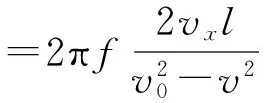
(20)
可见与介质静止时不同,在x=0的平面上的相位差仍然是一常量,但一般不为零.
令式(6)中y=0,即在x轴上,此时分成3个区间分别讨论如下.
1) 接收器在声源A的左侧,x<-l,则x+l<0,x-l<0.有
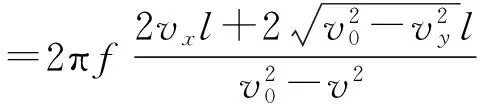
(21)
vx=0时,

(22)

(23)
2) 接收器在声源A、B的中间,-l

(24)
vx=0时,

(25)

(26)
3) 接收器在声源B的右侧,x>l,则x+l>0,x-l>0.

(27)
vx=0时,

(28)
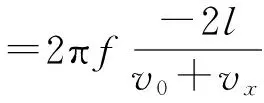
(29)
以上讨论说明vx和vy的变化都会改变x轴或x=0平面上的相位差,现以vy=0且vx≠0时为例,说明vx对以上位置处干涉情况的影响.将式(8)代入式(23),得
(30)
该式反映了在y=0且x<-l的区间内的干涉情况与vx的关系.在该区间的远场处两列波的振幅大致相等,干涉效果较明显.声波作为一种纵波,在该区间两列波行进方向和振动方向都相同,其干涉规律跟横波相同[2],即n为偶数时干涉相长,n为奇数时干涉相消.随着速度的变化,该区间内干涉相长与干涉相消会交替出现.在y=0且x>l的区间内的相位差由式(29)决定,其分析跟上述类似.
将式(8)代入式(26),得
(31)
该式反映了在y=0且-l (32) 由于在该区间两列波振动方向相同但行进方向相反,此时干涉规律与横波相反[2],即n为偶数时干涉相消,n为奇数时干涉相长.因此当vx=0时,n=0,此时该点干涉相消,当v增大时干涉相长与干涉相消会交替出现.由式(20)知,在x=0的平面上相位差都相等,但在该平面的远场处两列波行进方向和振动方向大致相同,干涉规律与横波相同.由此可见,在同一等相位差的双曲线(或双曲面)上的不同位置处声波的干涉情况不一定相同,这是纵波与横波干涉的不同之处. (33) 该式反映了在该区间内不同的n所对应的x随vx变化的规律.例如n=0时, (34)可见在该区间内相位差为零的点的x坐标正比于vx. 需要注意的是,干涉是质元振动位移的相加,各质元平衡位置的位移不变,即使是在干涉相消的位置处质元的速度也不为零.此外,相对于介质静止的情况,该问题除了干涉情况发生变化之外,质元的振动位矢也有所改变,本文未做详细分析.根据干涉图谱的变化情况可以计算出声源与介质的相对速度,利用这种方法可以测量流体的流速或物体运动速度. [1]漆安慎,杜婵英.力学[M].2版.北京:高等教育出版社,2009:366-367. [2]刘义春.纵波干涉的规律及其应用[J].物理通报,2000(9):11-13. Acoustic interference in uniform motion medium LV Ling-jie (College of physics and Electronics, Shandong Normal University, Jinan, Shandong 250358, China) In the paper, we discuss the interference of two sound waves engendered by static sound sources in the uniform motion medium, calculate the time distance of the equiphase waves simultaneously engendered by the two sound sources to a point. It is multiplied by the pulsatance to obtain the phase difference, then we get the equation of equiphase point. Finally, we discuss the interferences in several special positions and illustrate related applications. sound wave interference; moving medium; phase difference; longitudinal wave; velocity measurement 2015-05-05; 2015-07-31 吕令杰(1993—),男,山东宁阳人,山东师范大学物理与电子科学学院2012级本科生. O 422.5文献标示码:A 1000- 0712(2016)02- 0052- 04

