闵氏时空图在相对论教学中的应用

杨志万

(四川理工学院 理学院，四川 自贡　643000)



闵氏时空图在相对论教学中的应用

杨志万

(四川理工学院 理学院，四川 自贡643000)

将闵科夫斯基二维时空图应用于大学物理课程中的相对论教学，直观地揭示了狭义相对论时空观以及“尺缩钟慢”效应与“同时的相对性”的内在联系．

相对论教学；二维时空图；同时的相对性；“尺缩钟慢”效应；内在联系

在大学物理“狭义相对论”一章的教学中，只用洛伦兹变换公式以代数解析的方式，难以使学生深刻认识和体会相对论时空观．如何让学生尽可能深刻地理解狭义相对论时空观，如：同时的相对性、因果时序、“尺缩钟慢”效应与“同时的相对性”的内在联系，形成较为系统的知识结构，成了大学物理相对论教学的一个难点．教学中发现，在代数解析的基础上配合形象直观的闵可夫斯基时空图进行教学，学生不仅乐于接受，而且能起到事半功倍的教学效果．

1　闵科夫斯基二维时空图简介

狭义相对论诞生后，闵科夫斯基于1908年专门为相对论创立了四维闵氏几何[1](伪欧几何)．取横坐标代表三维空间坐标(通常只画出一维)，纵坐标ct代表时间坐标．由一维时间和三维空间构成的闵科夫斯基四维时空称为世界，任意一个事件在时空图上表示为一点称为世界点．随着时间的流逝，世界点在时空图上画出一条连续轨迹，称为世界线．为了在平面上形象地图示闵氏时空，通常采用由一维时间(ct)与一维空间(x)构成的二维时空图．将c与t相乘作为时间轴是为了保证各个坐标轴具有相同的量纲(现代单位制中c=1)．

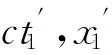
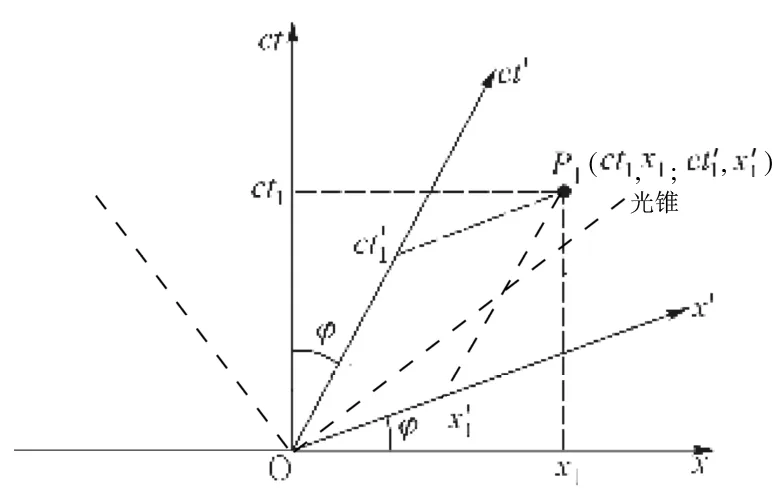
图1　闵氏二维时空图中的事件

2对同时的相对性的描述

由于在闵氏二维时空图中，S系的同时线平行于x轴，而S′系的同时线平行于x′轴，相对运动的两个惯性系的同时线不可能重合，所以不同惯性系必然具有不同的同时性．在S系同时异地的两个事件在S′系则成为了不同时事件(图2)，反之，在S′系同时异地的两个事件在S系则成为了不同时事件(图3)．

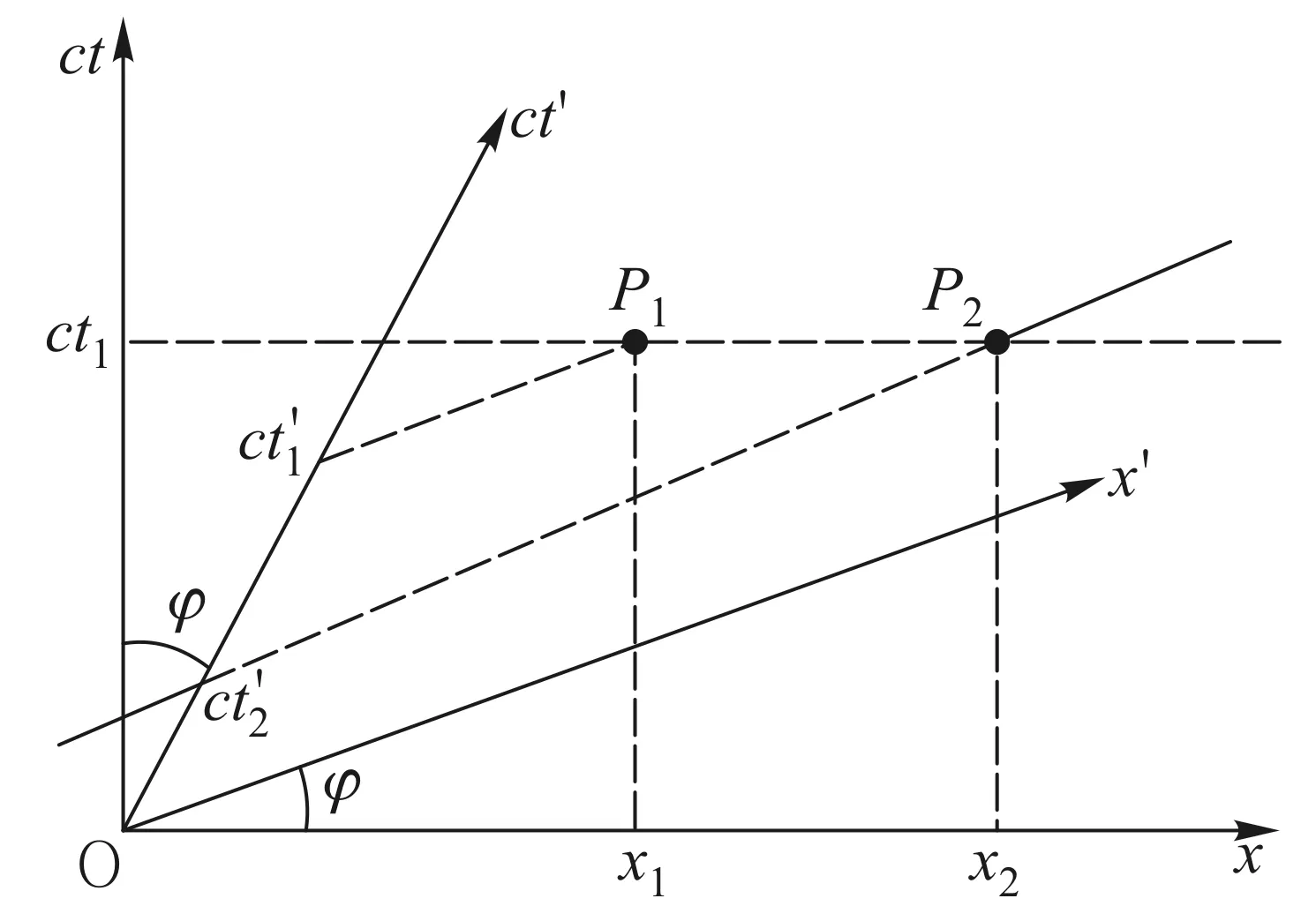
图2　S系的同时异地事件在S′系不同时

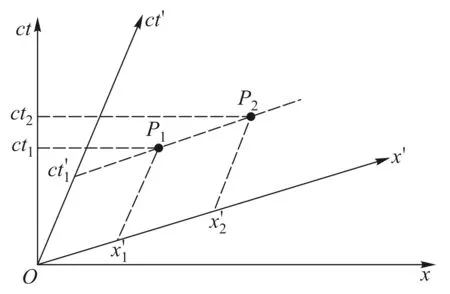
图3　S′系的同时异地事件在S系不同时

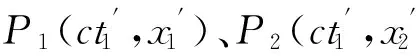
当且仅当两个世界点P1、P2在S系中重合时，在S′系观测它们也一定重合，分别具有相同的时间坐标和相同的空间坐标．所以，同时同地发生的两个事件，在任何惯性系观测都是同时(且同地)的．同地的同时性是绝对的．

3　对事件对的时序可否颠倒的讨论

由于同时线平行于x(x′)轴，必然位于类空区．当事件对P1P2的连线与ct轴夹角α>45°(类空事件对)时，事件对的时序可以颠倒．如图4所示，在S系中事件P1先于P2发生，在S′系观测则事件P1后于P2发生．当事件对P1P2的的连线与ct轴夹角α<450(类时事件对)时，事件对的时序不可能颠倒．如图5所示，在S系中事件P1先于P2发生，在S′系观测仍然是事件P1先于P2发生．

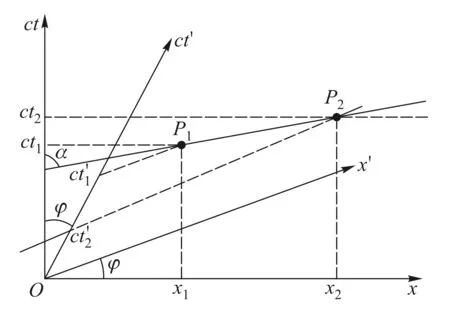
图4　类空事件对的时序可以颠倒

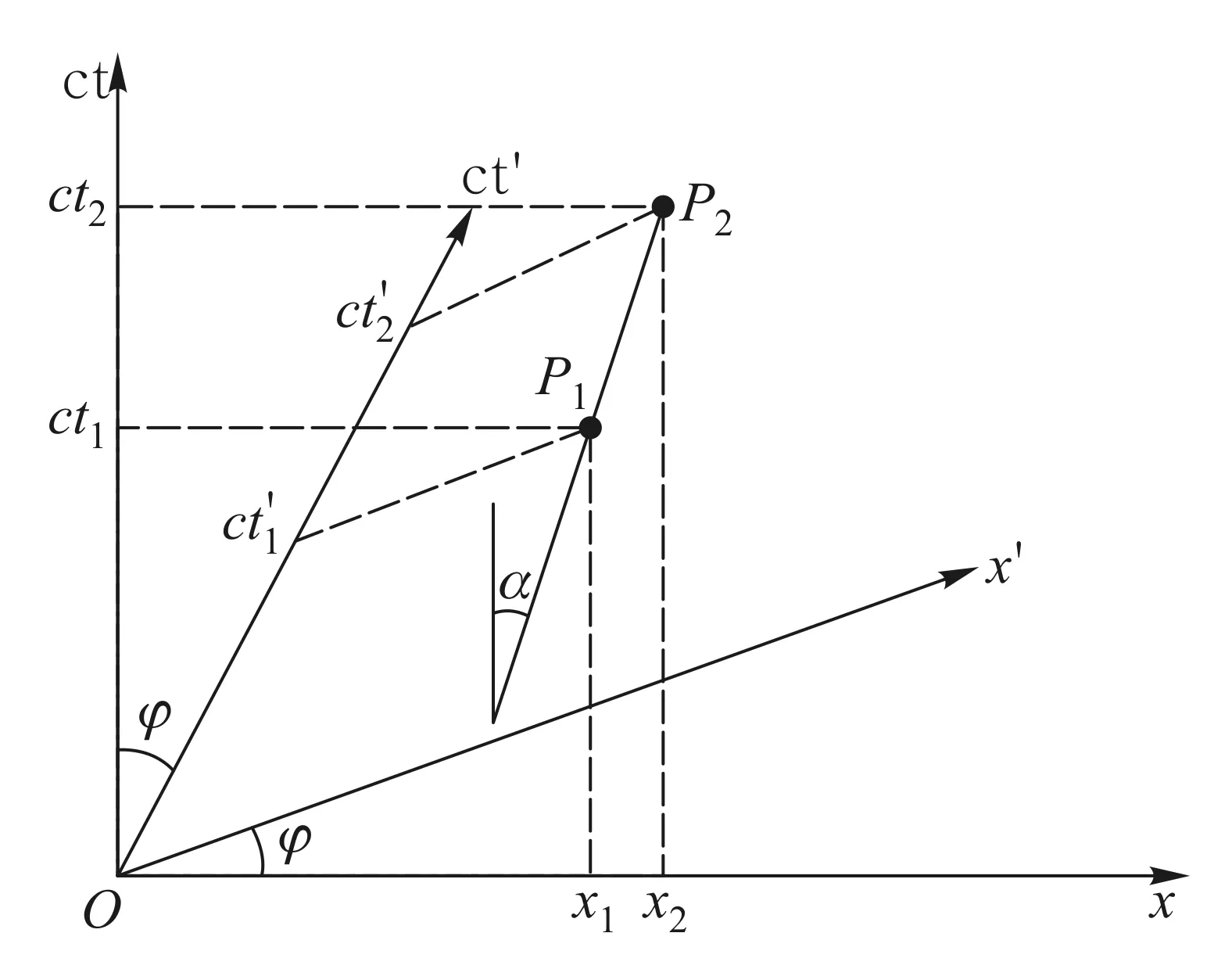
图5　类时事件对的时序不能颠倒

4　“动尺收缩”与“同时的相对性”的内在联系

爱因斯坦在“光速有限且绝对不变”的启发下，通过理想实验得出了“同时的相对性”的重要结论．同时的相对性意味着各个惯性系各有自己的同时标准，不同观测者对“是否同时”的认知不同，导致他们对同一段长度及同一段时间的观测结果不同，这就是狭义相对论最为人熟知的“动尺收缩”和“动钟变慢”效应．搞清“尺缩钟慢”效应与同时的相对性的内在联系，是理解相对论时空观的关键．同时的相对性正是爱因斯坦建立狭义相对论时空观的突破点．

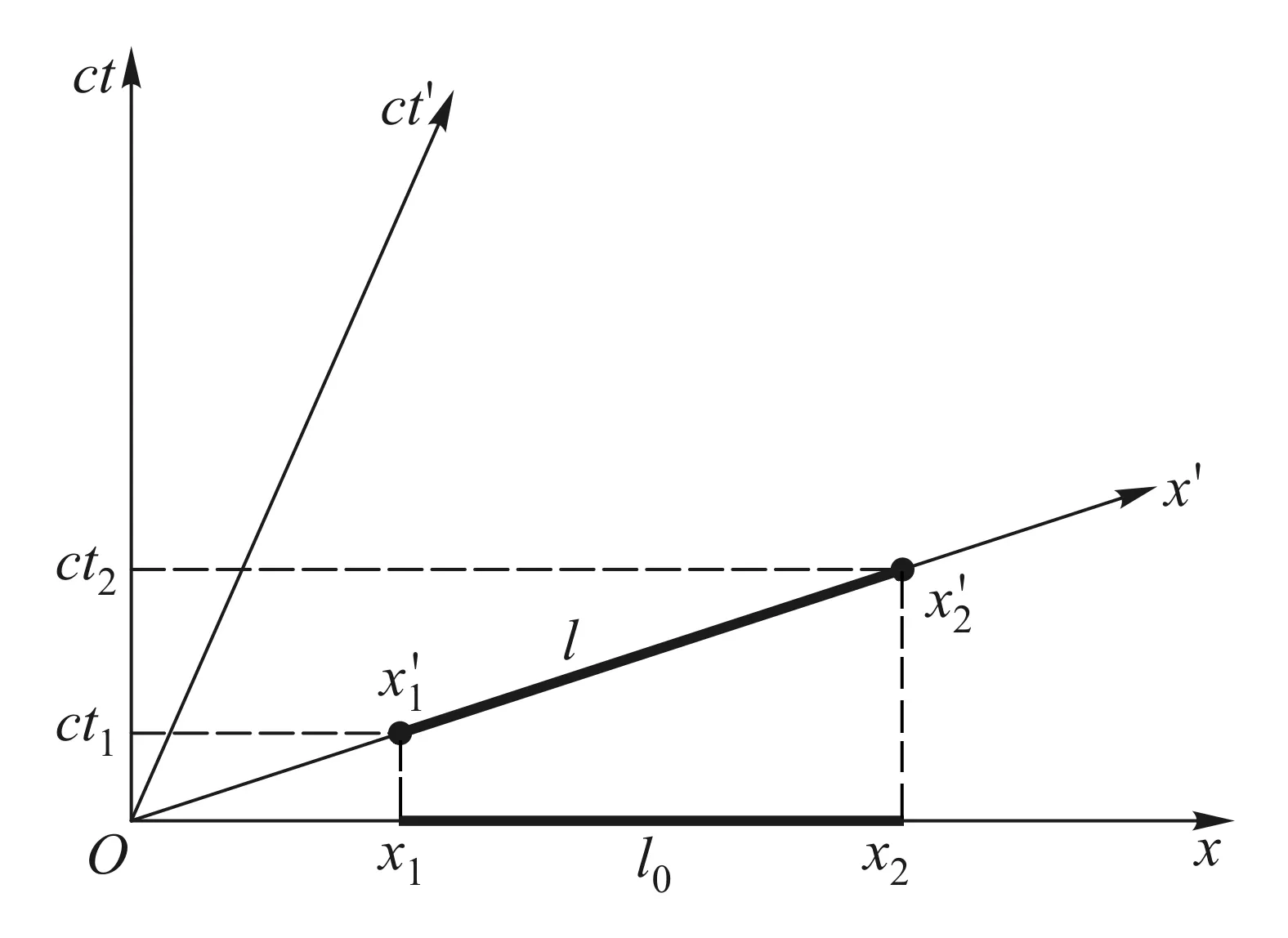
图6　长度佯谬时空图

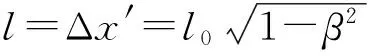
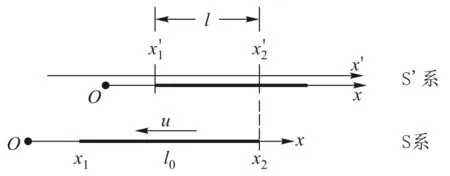
图7　相对运动对长度测量的影响

5　“动钟变慢”与“同时的相对性”的内在联系

异地的同时性总是相对的，甚至两个异地事件发生的先后顺序都有可能颠倒，只有同地的同时性才是绝对的．所以，在相对论中比较两个异地时钟是无意义的，只有在同一地点才能施行对钟，比较时刻的先后及示数大小，测量时间间隔．

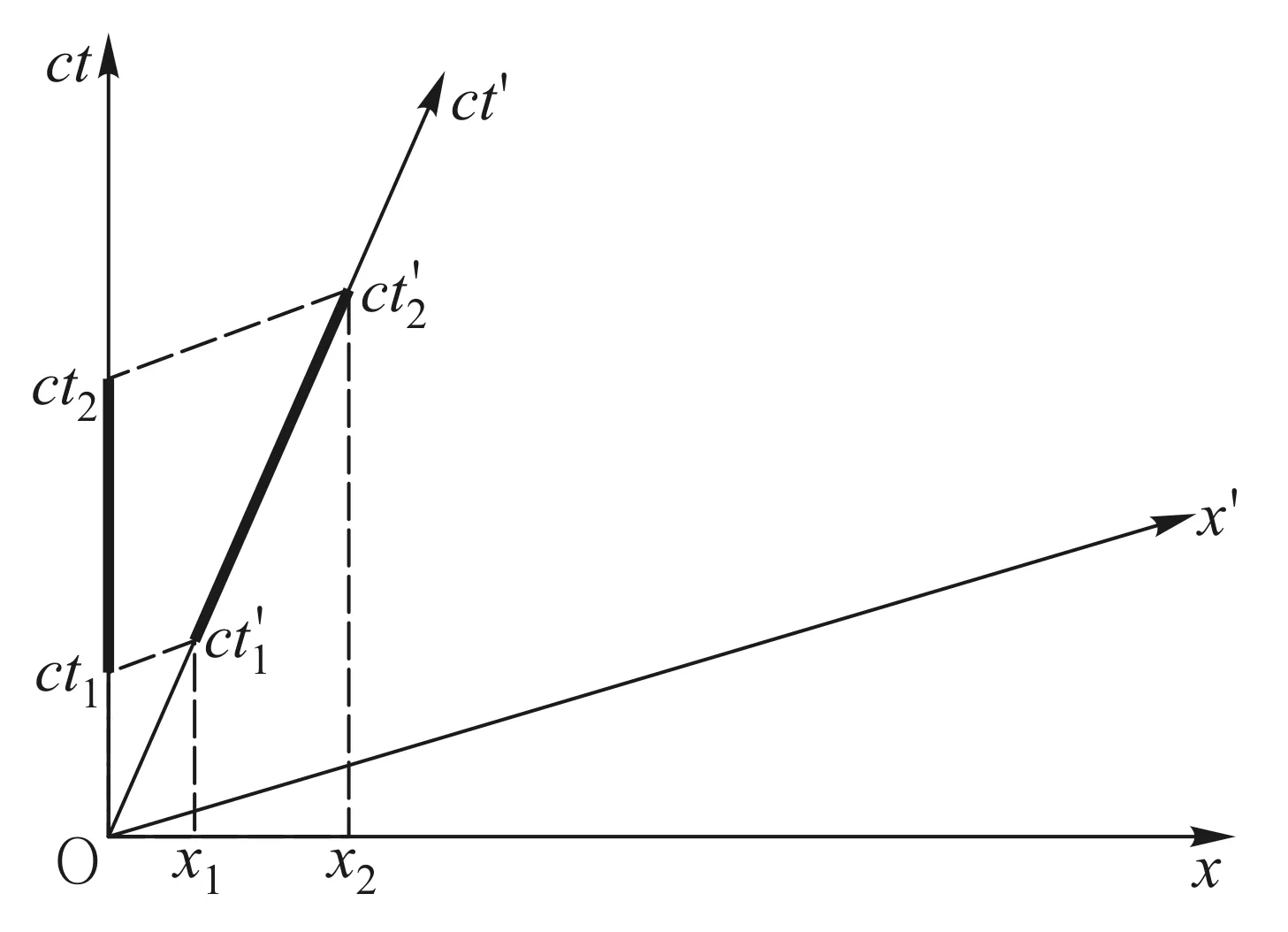
图8　时钟佯谬时空图

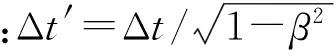
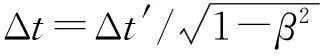
6　“尺缩效应”与“钟慢效应”的本质

上述对“尺缩钟慢”效应的讨论只适用于相互匀速直线运动的惯性系，对于非惯性系(两坐标系中至少有一个相对于惯性系有加速度)不在本文讨论的范畴．

综上所述，不同的惯性系各自拥有自己的标准尺和标准钟，当它们彼此比较时，总是发现做相对运动的对方“尺缩钟慢”． 如果没有加速度，仅仅因惯性运动引起的“尺缩钟慢”效应，在本质上只是一种“观测性真实”(时空性质)．观测者站在各自的同时性立场，都认为客体原系测出的长度和时间才是真实长度(固有长)、真实时间(固有时)，相对于客体运动的他系观测出的长度和时间分别小于真实长度、大于真实时间．其根本原因在于相对运动改变了他系对客体的同时性的定义，致使其对“同时”及“同地”的认知发生了改变．但客体的固有长度并不因惯性运动而缩短，时钟的固有频率也并不因惯性运动而放缓．所以，客体原系对客体测出的固有长和固有时才是不受相对运动影响的“绝对性真实”(客观存在)．但这并意味着在他系就不能对客体做出绝对性真实的判断，在他系中测量客体，必须根据“尺缩”和“钟慢”两种效应做出全面的判断，才能得出客观真实的结论．注意到客体尺缩的同时，还必须考

虑到客体的钟也更慢；注意到客体钟慢的同时，还必须考虑到客体的尺也更短．否则，只凭两种效应中的一种就妄加判断，得出的一定是片面甚至虚假的结论．

[1]刘辽,费保俊,张允中．狭义相对论[M]．北京：科学出版社，2008：42-44．

Application of the Minkowski space-time diagram to teaching of the Einstein theory of relativity

YANG Zhi-wan

(College of Science, Sichuan University of Science and Engineering, Zigong, Sichuan 643000, China)

In this article, the two-dimensional Minkowski space-time diagram is applied to teaching of the Einstein theory of relativity in college physics, and there is an intuitive reveal on the inner connections between simultaneous relativity and space-time in special relativity as well as time dilation and length contraction.

teaching of the Einstein theory of relativity; two-dimensional space-time diagram; simultaneous relativity; time dilation and length contraction effect; intrinsic connection

2015-03-02；

2015-09-11

杨志万(1963—)，男，四川平昌人，四川理工学院理学院副教授，硕士，研究方向：物理教育、理论物理．

O 412.1

A

1000- 0712(2016)02- 0027- 03