充电圆平行板电容器的电磁场分布
江俊勤
(广东第二师范学院 物理系,广东 广州 510303)
充电圆平行板电容器的电磁场分布
江俊勤
(广东第二师范学院 物理系,广东 广州510303)
用Mathematica对充电圆平行板电容器的电磁场进行详细的数值研究; 给出了电容器内外的电势、电场强度以及磁感应强度的空间分布;讨论了电场和磁场的边缘效应.
充电圆平行板电容器; 极板电流; 位移电流;电磁场; 边缘效应;数值分析
在电磁学的教学中,有许多在似稳条件下计算充-放电时圆平行板电容器内外位移电流密度和磁感应强度的例子. 这些教材和学习指导书[1-3]对这个问题的算法思路如下.
忽略电场的边缘效应,即假设电场只存在于电容器内部而且是均匀分布的,则有:
(1)
利用I=dQ/dt就可以求得位移电流密度:
(2)
由于问题具有良好的对称性,磁场可用全电流定律
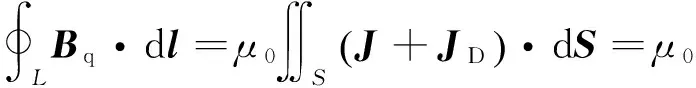
(3)
来计算.取回路L为半径等于x的圆周,由此容易求得磁感应强度:
(4)
这种算法简单快捷,但存在两个缺点:
1) 忽略边缘效应得到的E、JD和Bq存在多大的误差?什么情况下可以忽略边缘效应?都无法讨论.
2) 容易使人误以为磁场是由位移电流(即变化的磁场)产生的. 事实上,有的资料[2]在其计算后的注释中就是这样认为的(这是上述解法的最大隐患).
根据文献[4]的介绍,早在1974年就有人企图在似稳条件下,通过检测充-放电时圆平行板电容器内的磁场来验证位移电流可以激发磁场.
该实验的大意是:把一个螺绕环形线圈(下面简称螺绕环)放在一个圆平行板电容器两极板中间(极板为半径R=50~80 cm的铝板,两极板的间距为2a),在电容器两极板上接上一个频率为20 kHz的低频电源. 该实验旨在探测位移电流激发的磁场在螺绕环中引起的电动势,并把这一电动势在示波器上显示出来. 图1为该装置的截面图,小圆圈是螺绕环的截面,圆点P和交叉号是螺绕环中的磁场方向.
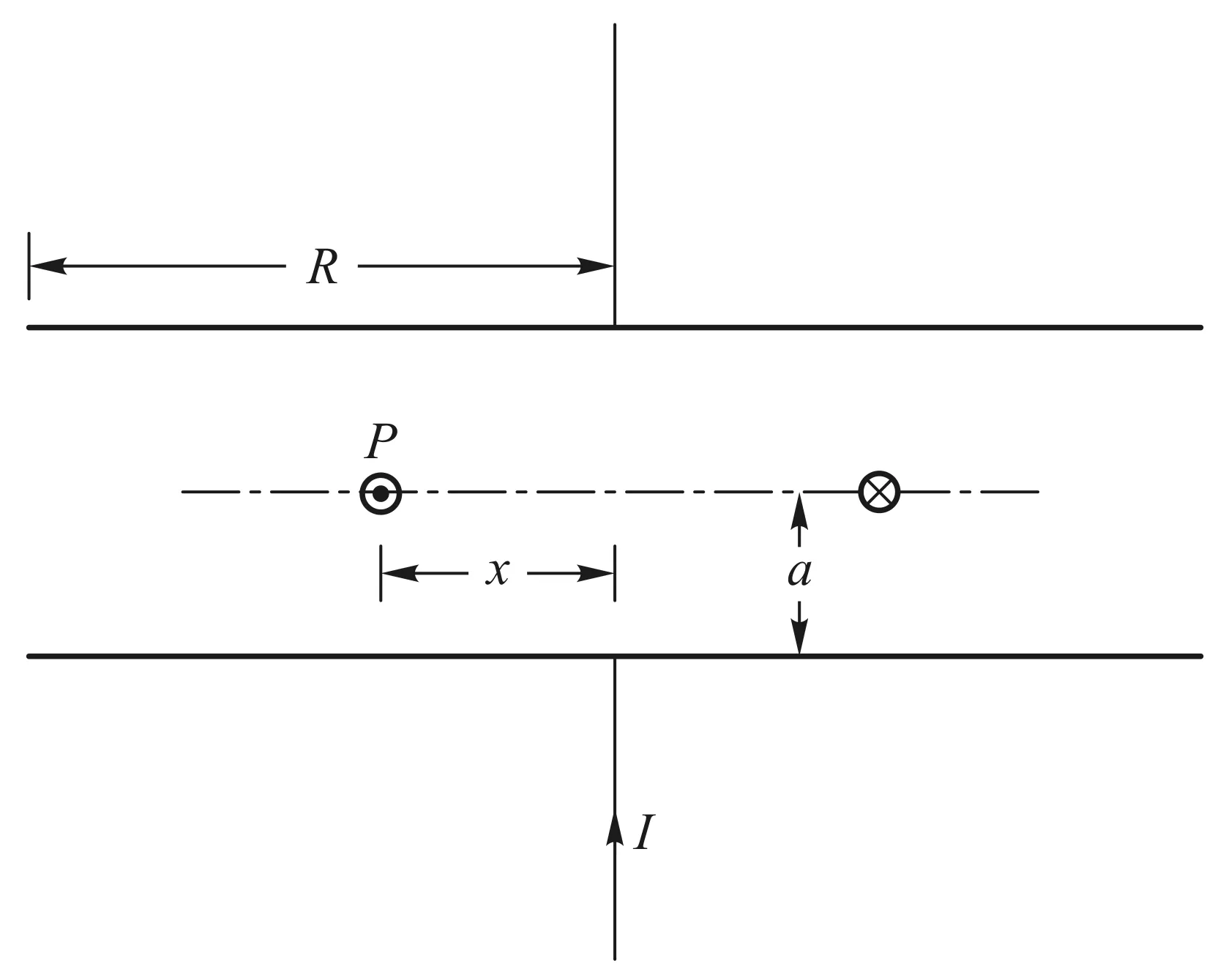
图1 圆平行板电容器与螺绕环的截面图
虽然早就有文章[4]指出该实验的理论依据是不对的,结论也是错的,是一个典型的张冠李戴的实验. 但是该理论比较深奥,不容易理解,以致于几十年来一直有教师(特别是高中教师)在做这类演示试验.
如果能对图1中传导电流的磁场进行具体的计算,将有帮助于理解电容器内的磁场的起源. 所以文献[5]把圆平行板电容器实验中的传导电流分为极板电流和馈线电流两部分,用毕-萨定律计算极板电流和馈线电流的磁场,并与使用全电流定律的计算结果(即式(4))作比较,通过全电流(J+JD)的磁场等于传导电流(J)的磁场来证明位移电流(JD)的磁场为零. 这是一个很好的方案,但是由于圆平行板电容器极板电流磁场的计算十分复杂,该文只能在x<
由此看来,对充电圆平行板电容器的电场和磁场进行全面的数值分析,将有帮于全面认识该电磁场的空间分布、正确理解平行板电容器内部磁场的起源,以及弄清忽略边缘效应会产生多大误差.
本文用数值计算的方法全面研究充电圆平行板电容器内外的电磁场分布. 这里的电磁场分布,是指低频交流电源处于给电容器充电阶段的半周期内(或直流电源充电)的某一时刻电磁场的空间分布. 放电时情况类似,只是方向相反.
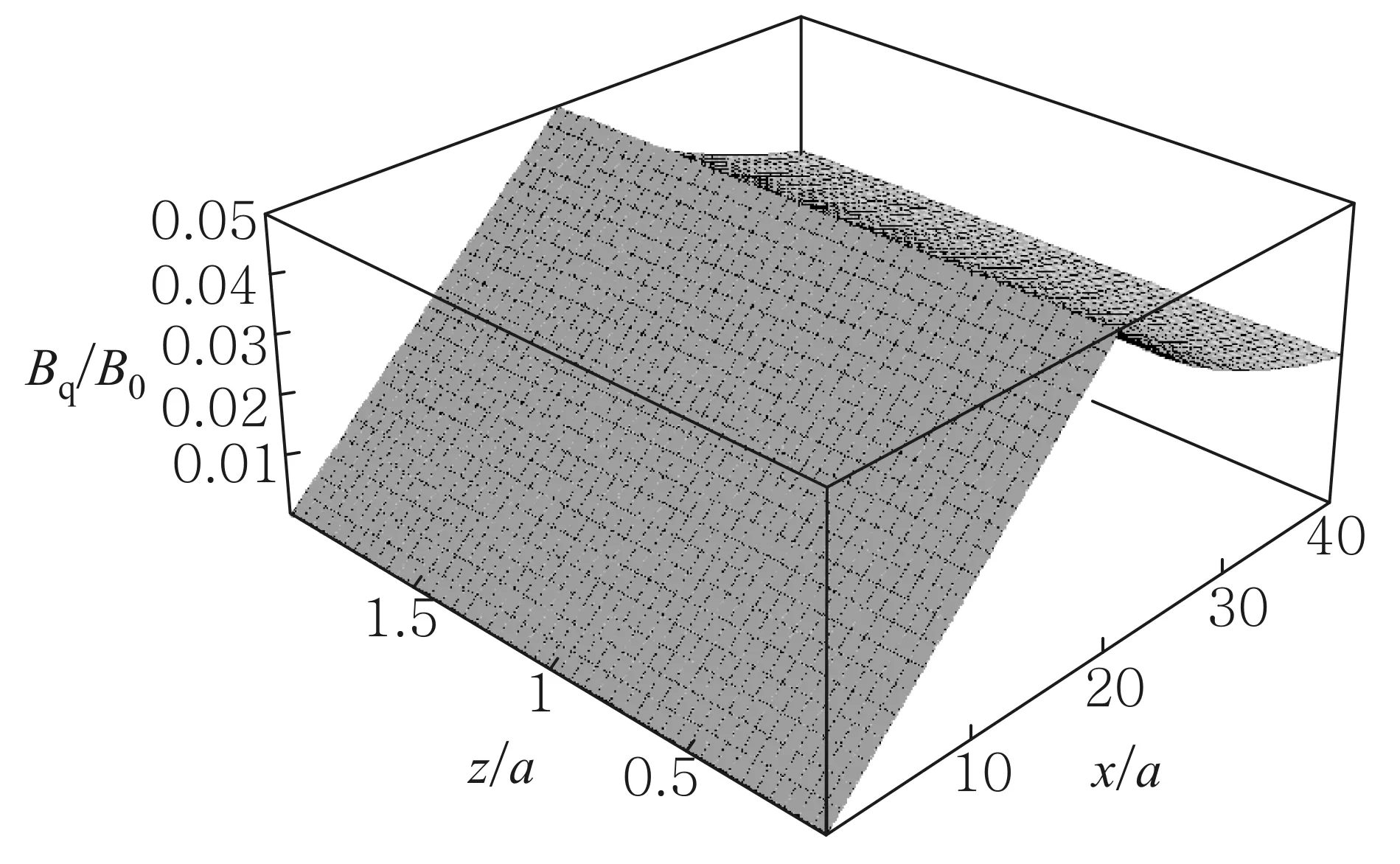
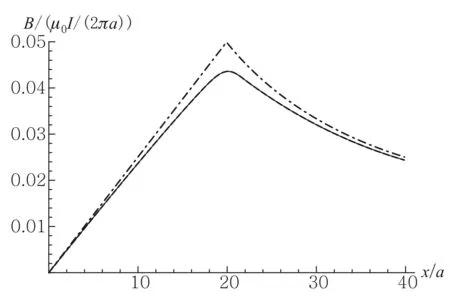
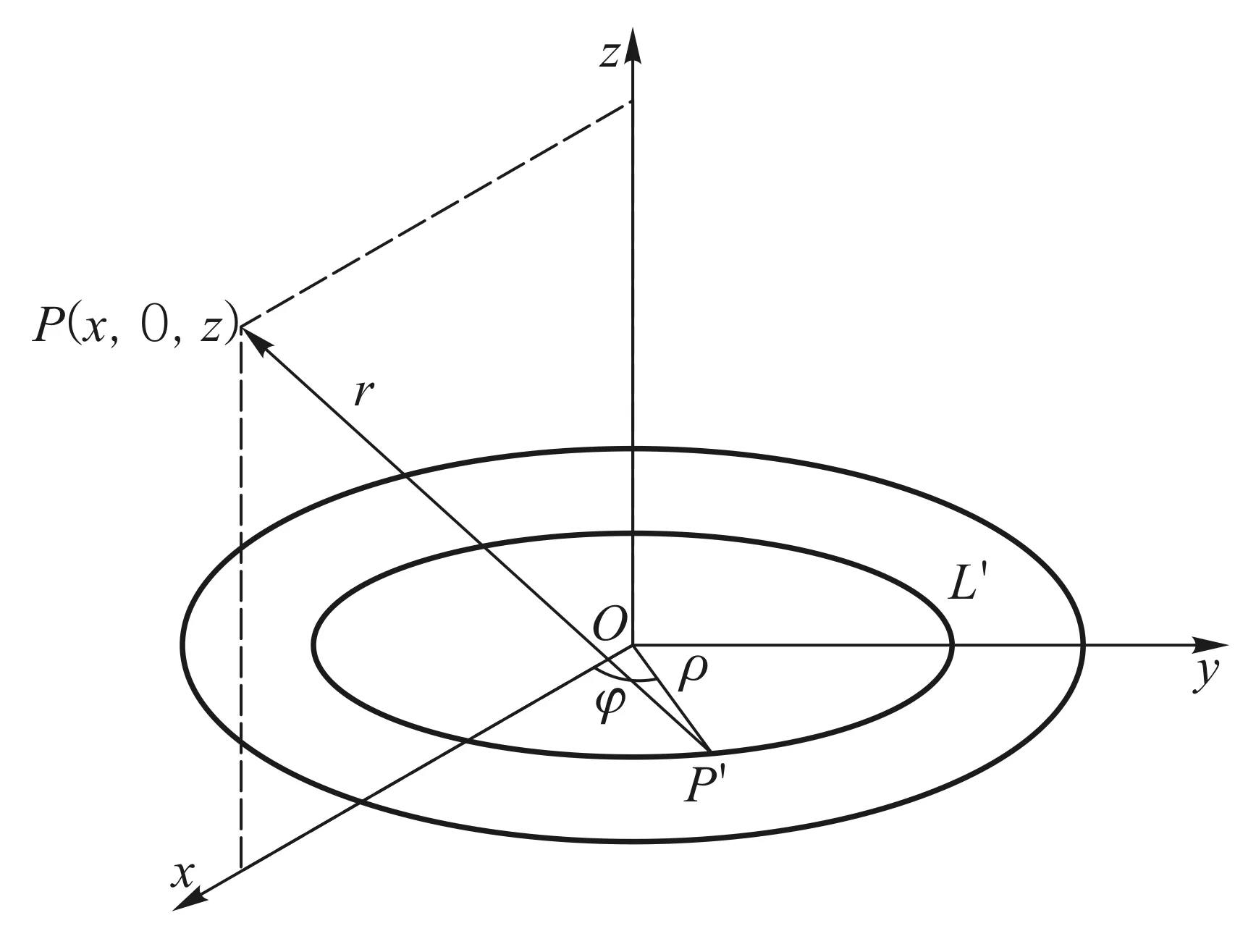
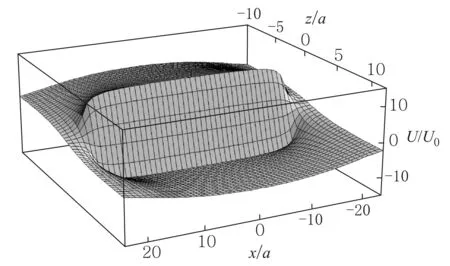
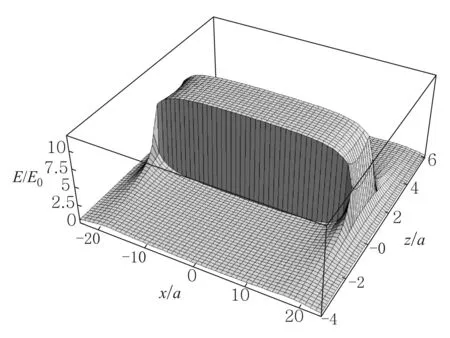
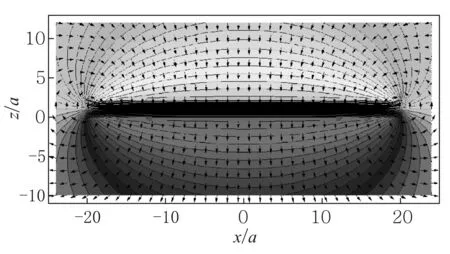
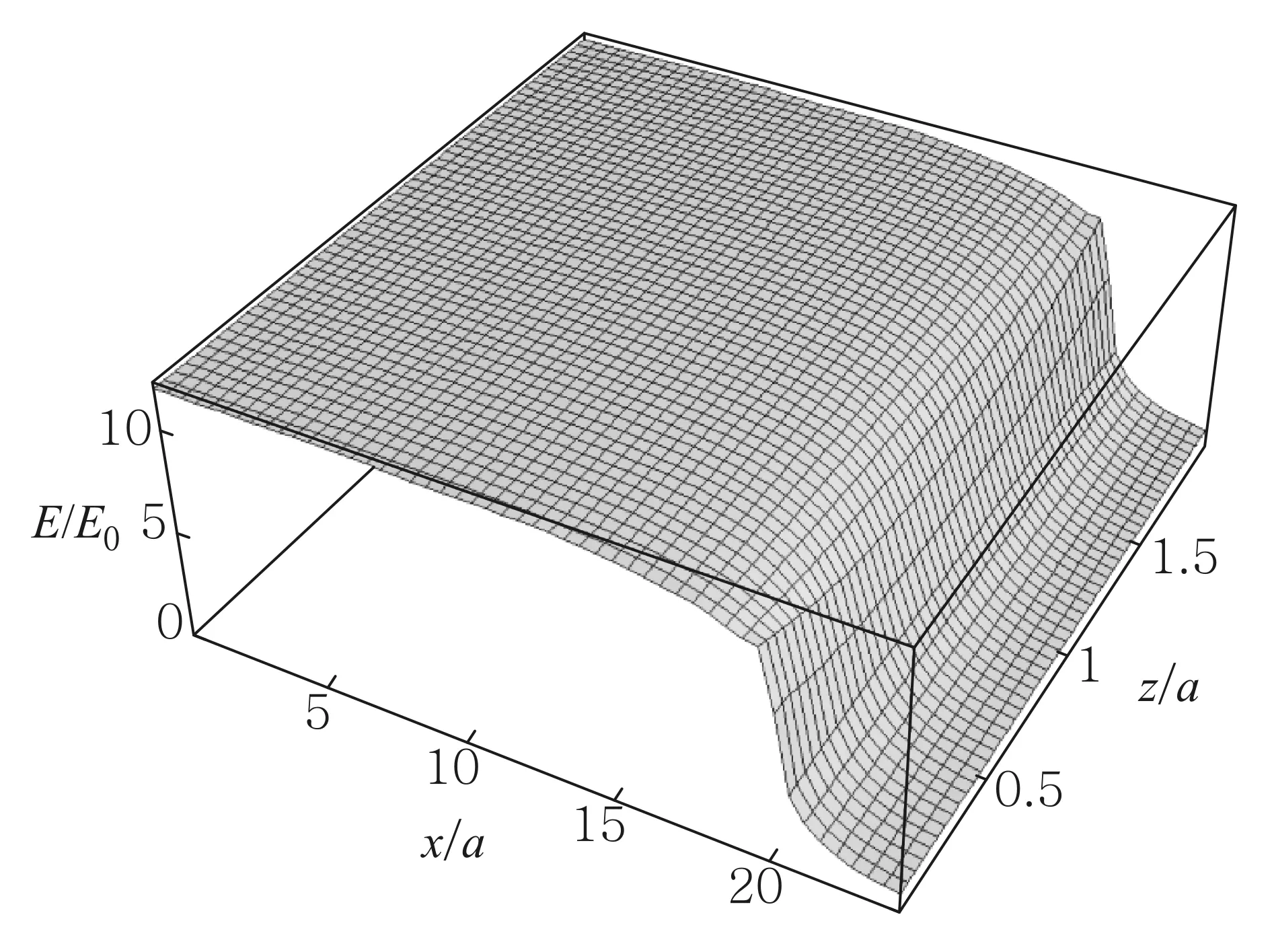
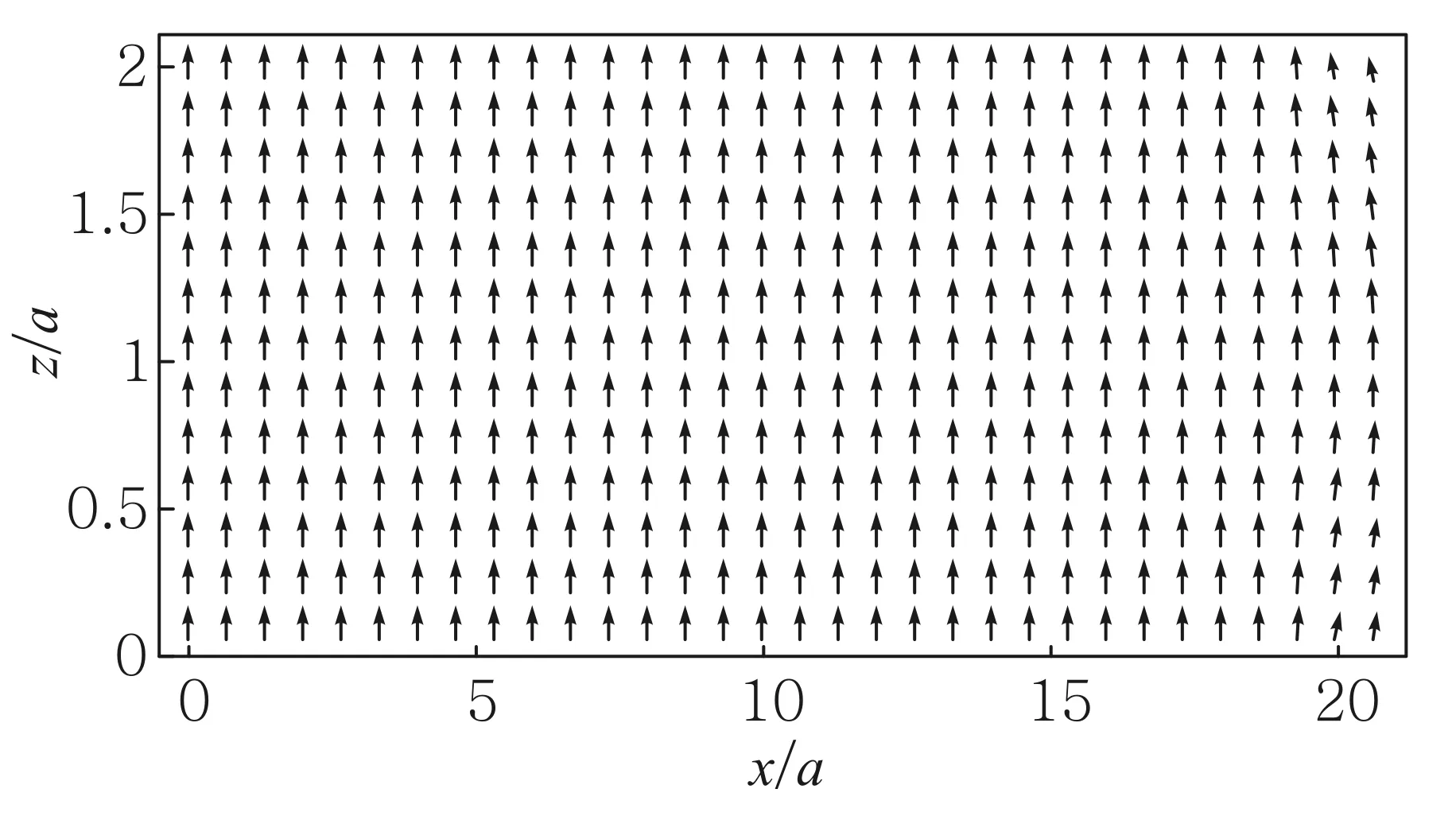
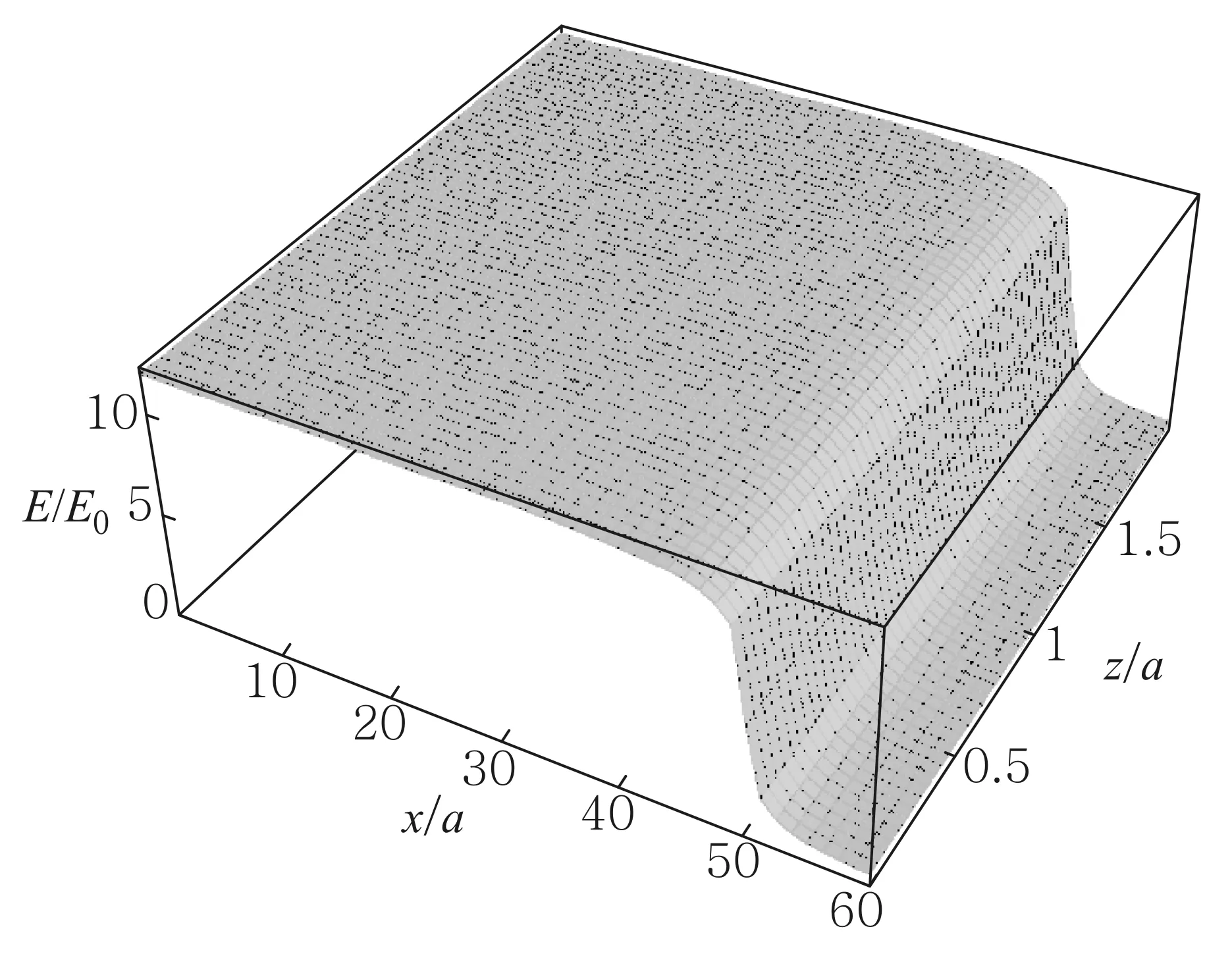
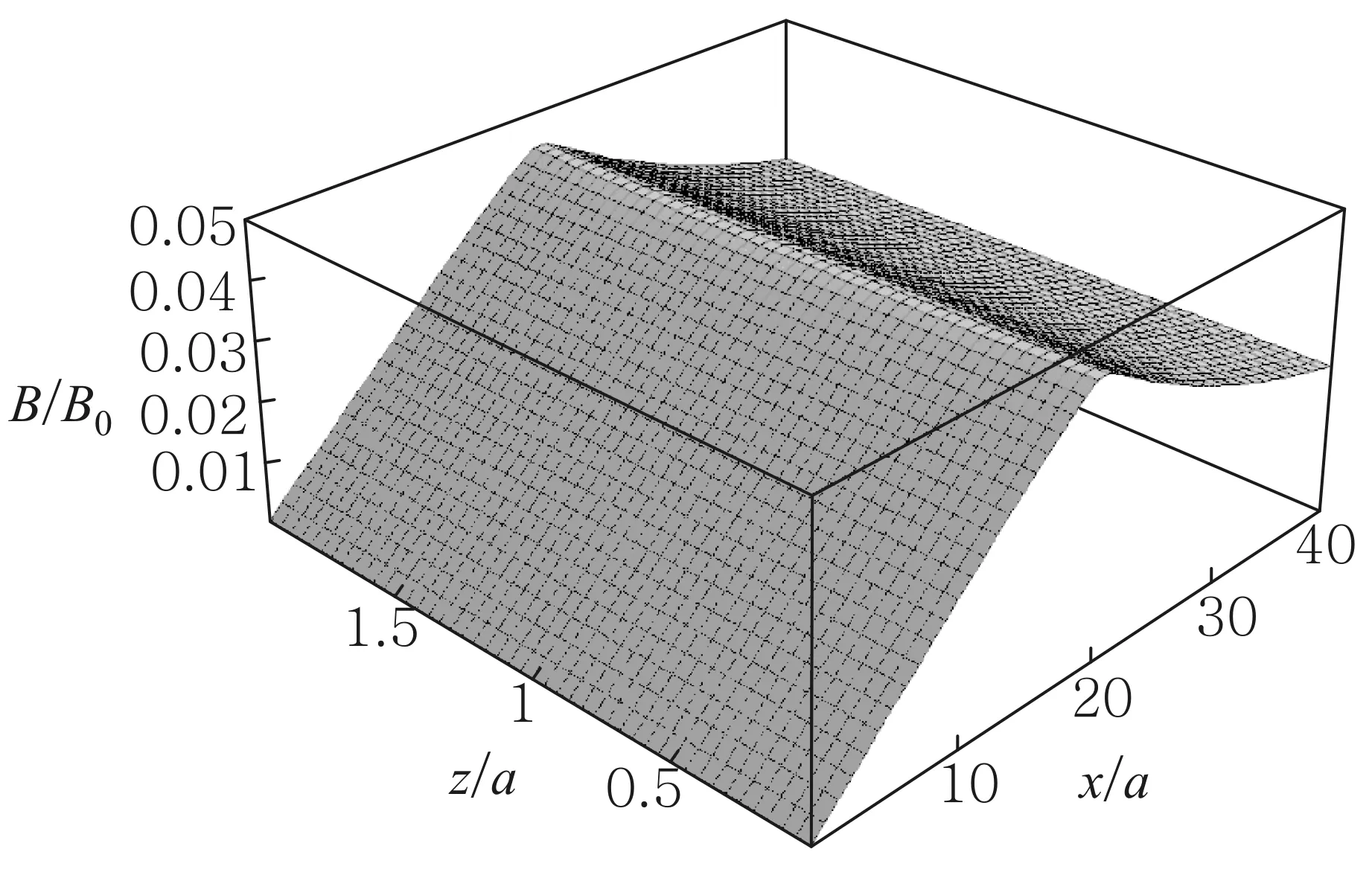
电容器两极板是直径为2R的圆,相距为2a. 在a< 先计算下极板电荷激发的电场.圆盘由一系列同心圆环组成,如图2所示,由于具有轴对称性,故只需考虑xOz平面内的观测点P(x,0,z)的电场分布,设下极板面上电荷元P′点离圆心的距离为ρ, 其坐标为(ρcosφ,ρsinφ,0),则P′到观测点P(x,0,z)的矢径和距离分别为 r=(x-ρcosφ)i-ρsinφj+zk, (5) 图2 下极板与坐标系 由叠加原理,得下极板电荷激发的电势: 所以两个均匀带电薄圆盘激发的电势为 (6) 而电场强度为 (7) 式(6)和式(7)是十分复杂的二重积分,没有解析解,可以先对φ积分并把结果表示为椭圆积分,而对ρ的积分则使用Mathematica内置的数值积分法,可以把圆平行板电容器内外的电势和电场强度做统一的计算和绘图.先取R/a=20,以a为长度单位、U0=Q/(4π2ε0R)为电势单位、E0=Q/(4π2ε0R2)为电场强度单位,图3—图5给出了较大范围的整体分布图;图6和图7给出了电容器内部及边缘附近的局部分布图. 图3—图7显示:1)电源给电容器充电时,下极板的电势呈现出圆心处最强、越外面电势越弱的分布,这保证了电流从圆心进入下极板后向外辐射,正电荷不断累积;上极板圆心处电势最小,电子从圆心进入极板后向外辐射,电子(带负电荷)不断累积. 2) 在R/a=20 (即直径为极板距离的20倍)的情况下,虽然电场主要集中在电容器内部,但是边缘效应很明显,电场的空间分布与式(1)有较大差距,不但只有在中间区域内(例如x∈[-R/2,R/2])才接近均匀分布,而且在电容器边缘附近的极板外上下两侧(x≈±R,z<0,z>2a)的电场也比较强; 比值R/a越大,边缘效应越小,R/a→∞时边缘效应完全消失,但是在直径增大为极板距离的50倍 (即R/a=50)时,边缘效应仍然比较明显,如图8所示. 图3 当R/a=20时, 充电圆平行板电容器的电势分布 图4 当R/a=20时, 充电圆平行板电容器电场强度大小的分布 图5 当R/a=20时, 充电圆平行板电容器等势线和电场方向的分布 图6 当R/a=20时, 充电圆平行板电容器电场强度大小的分布(内部及边缘附近) 图7 当R/a=20时, 充电圆平行板电容器电场强度方向的分布(内部及边缘附近) 图8 当R/a=50时, 充电圆平行板电容器电场强度大小的分布 2.1极板电流磁感应强度的积分表达式 显然,在图1所示的圆平行板电容器实验装置中,位移电流(即变化的电场)和传导电流都是存在的,传导电流可分为馈线电流和极板电流两部分,它们都可以在电容器两极板之间产生磁场.为了计算任意x值处的磁场,必须先导出极板电流磁感应强度的积分表达式,像文献[5]一样,设馈电导线沿电容器轴线延伸到无限远处. 先计算下极板电流产生的磁感应强度B1. 这个问题是关于z轴对称的,只需研究xOz平面中在x≥0且0 如图2所示,过极板上的P′点作圆L′ (准确地说,L′是短圆柱,极板的厚度就是圆柱的长度,用b表示,b很小),设流经L′的电流密度为J(方向沿圆盘径向),则流出L′的电流为i=2πρbJ. 由电流连续性,有 I-2πbρJ=dq/dt 式中q为L′所包围的电荷. 因电荷在极板上时刻保持均匀分布, 故 式中Q为总电荷. 总电荷量Q随时间变化,Q与I的关系为I=dQ/dt, 所以 (8) 所以流出L′的电流强度为i(ρ)=2πbρJ=I(1-ρ2/R2), 它随ρ的增大而减小,i(0)=I,i(R/2)=0.75I,i(R)=0. 这与图3的电势分布规律相映成趣. 极板上电流密度矢量为 J=Jcosφi+Jsinφj (9) 把式(9)和式(5)代入毕-萨定律: 得下极板电流在点P(x,0,z)处产生的磁感应强度为 B1x=B1z=0(既无径向分量也无轴向分量), (10) 式(10)是复杂的二重积分,如何计算这个二重积分是解决本问题的关键. 先对ρ积分,并记为 再对φ积分,则式(10)可写成 人工推导f(x,z,φ)的表达式需要一定的技巧,其过程也颇为复杂,我们把这个推导工作交由Mathematica自动快速完成,结果为 (11) 由对称性可知,两个极板上的电流在P(x,0,z)点处共同产生的磁感应强度为 Bb=B1y+B2y= z,φ)]cosφdφ (12) 式(12)不能用初等函数表示,下面用Mathematica内置的数值积分法求解. 2.2极板电流和馈线电流总磁场的数值结果 由式(11)和式(12),经数值积分可以得到极板电流产生的磁场Bb与坐标x和z的函数关系.用毕-萨定律容易算出两边无限延伸的馈线电流在P点产生的磁感应强度: (13) 所以极板电流和馈线电流共同产生的磁场为B=Bb+BL. 取R/a=20,以B0=μ0I/(2πa)为磁感应强度的单位,根据式(11)—式(13), 可求得极板电流和馈线电流产生的总磁场B(=Bb+BL),结果如图9所示. 磁场的分布明显与x有关,但几乎与z无关,也就是说:由于极板的直径远大于极板的距离(20倍),所以只要螺绕环与极板共轴放置,不论是放置在正中间,还是放置在一边(离一个极板近、另一个极板远),所在处的磁场几乎是一样的. 图9 当R/a=20时,极板电流磁感应强度和馈线电流磁感应强度的总结果 3.1忽略边缘效应的结果 现有的教科书、题解和论文[1-3]在用全电流定律计算磁感应强度时都是忽略边缘效应的. 为了便于讨论,现将忽略边缘效应的结果即式(4)绘制成图,如图10所示. 图10 当R/a=20时,用全电流定律计算得到的磁感应强度(忽略边缘效应) 由图9和图10可见:由全电流定律计算得到的磁感应强度Bq, 与极板电流和馈线电流磁感应强度的叠加结果B=Bb+BL有明显的差别. 所以通过图9和图10的对比还不能说明“位移电流对磁场的总贡献为零”. 人们可能会问:这个差别会不会就是位移电流对磁场的贡献呢?如果是的话,那么在图1所示螺绕环中的磁场有一部分是位移电流的贡献. 但是图9和图10的差别完全是由于忽略边缘效应造成的. 为了验证这个论断,下面以电容器两极板平分面(即z=a平面)上的观测点为研究对象,根据第1节已经得到的电场分布,重新用全电流定律计算磁感应强度(对磁场的分布进行修正),再与B=Bb+BL做比较. 3.2在考虑边缘效应情况下用全电流定律计算磁感应强度 如图4—图6所示,即使在电容器两极板的平分面上,电场大小的分布也是复杂的,没法得到严格的解析式. 为了获取电场的这个真实而复杂的分布信息,可以使用Mathematica的插值函数来逼近z=a平面上的电场分布. 把电场强度表达式改写成 (14) 当x≤R时取k=1、当x>R时取k=0, 就退化为忽略边缘效应的情况;若考虑边缘效应,则k是插值函数. 相应地,位移电流密度表达式改写成 (15) 代入全电流定律,即式(3), 得磁感应强度的积分表达式 (16) 考虑0≤x≤2R区域(当x>2R时, 电场强度可以取为零),为了获得准确的多项式插值函数k,把该研究区域划分为4个子区域,取R/a=20,以a为长度单位,得函数k如下: 当0≤x≤14时, k=(4π)-1(11.938836+0.0028799705x- 0.0027373809x2+0.00026194870x3- 0.000016930655x4); 当14≤x≤20时, k=(4π)-1(-1224.2772+537.36118x-96.010951x2+ 9.0497529x3-0.47563545x4+ 0.013239062x5-1.5272096×10-4x6); 当20≤x≤26时, k=(4π)-1(53031.071-12755.333x+1278.9328x2- 68.408628x3+2.0584056x4- 0.033031236x5+2.2081749×10-4x6); 当26≤x≤40时, k=(4π)-1(9.1845855-0.72488490x+0.019386526x2- 0.00017427419x3) (17) 为了检查插值函数的准确性,把式(17)代入式(14),并把计算结果与第1节电场分布的原始数据绘制在同一张图中,如图11所示,两者很好一致,所以式(14)和(17)很好地描述了z=a平面上的实际电场分布,由它们可以快速准确地求出与中心轴距离为x处的电场强度(0≤x≤2R). 图11 当R/a=20和z=a时,电场强度多项式插值函数与原始数值的比较.实线:插值函数的结果;长划线:原始数值结果 把式(17)代入式(16)可以得到Bqk与x的函数关系. 为了便于比较, 把Bqk、Bq和B=Bb+BL与x的关系画在同一张平面曲线图上,如图12所示. 由以上的数值结果,可得如下结论: 1) 用毕-萨定律求得的传导电流的磁感应强度(Bb+BL)与用全电流定律(考虑边缘效应)求出的磁感应强度(Bqk)是完全一致的.Bqk=Bb+BL说明:在似稳条件下,螺绕环内的变化磁场完全是由变化的传导电流产生的,位移电流对磁场的总贡献为零;图9所示的磁场既是传导电流的磁场也是全体电流的磁场. 即使把低频电源(f=20 kHz)改为高频电源,例如f=30 MHz,对应的波长(λ=10 m)仍然远大于极板间距(d=5 cm),电容器内部仍然是近场似稳区,磁场仍主要来自传导电流的贡献(位移电流的贡献可以忽略);只有使用极高频电源(例如分米波、f=3000 MHz),位移电流对电容器内部磁场的贡献才不可忽略. 图12 当R/a=20和z=a时,磁感应强度三种结果的对比.实线为Bqk(考虑边缘效应) ,点划线为Bq(忽略边缘效应),长划线为B=Bb+BL 2) 用全电流定律计算磁感应强度时,如果忽略边缘效应,那么计算结果将明显偏大,特别是在圆盘边缘附近 (在x=R处偏差最大,约为15%);只有在x< 进一步的研究表明:减小极板距离,可以降低边缘效应. 当R/a=50时,忽略边缘效应后,在|x|≤R/2或|x|≥3R/2范围内影响很小,但是在边缘附近仍然有较大偏差(在x=R点处偏差最大,大约为6.8%).相反,增大极板的距离,边缘效应也明显加大,当R/a=10时,忽略边缘效应带来的偏差可达到27.4% [1]哈里德D,等. 物理学基础[M]. 张三慧,李椿,等,译. 北京:机械工业出版社,2005:805-814. [2]王小力,张孝林,徐忠锋. 大学物理学习指导典型题解[M]. 西安:西安交通大学出版社,2009: 150-153. [3]刘克哲,张承琚. 物理学(第三版)学习指导书[M].北京:高等教育出版社,2006: 321. [4]朱久运.关于位移电流激发的磁场[J].大学物理,1983, 2(11): 9-12. [5]李元勋. 用毕-萨定律计算圆平行板电容器极板上电流的磁场[J].大学物理,1996, 15(1): 22-24. Electromagnetic field from a charging circular parallel plate capacitor JIANG Jun-qin (Department of Physics, Guangdong University of Education, Guangzhou, Guangdong 510303, China) The electromagnetic field from a charging circular parallel plate capacitor is numerically studied by using the Mathematica. The spatial distributions of the electric potential and the electric field intensity as well as the magnetic induction intensity are given. The edge effect of the electromagnetic field is discussed. charging circular parallel plate capacitor;plate current;displacement current;electromagnetic field;edge effect;numerical analysis 2015-03-02; 2015-08-25 广东省高等学校专业综合改革试点项目(XM060012物理学)资助 江俊勤(1962—),男,广东揭阳人,广东第二师范学院物理系教授,主要从事理论物理教学和格点规范场论的研究工作. O 442 A 1000- 0712(2016)02- 0021- 061 充电时电容器内外的电场分布
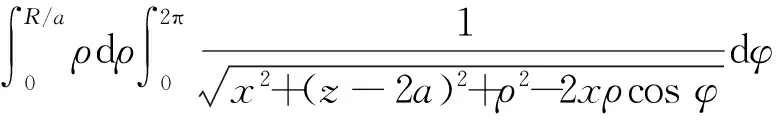
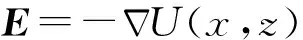
2 充电圆平行板电容器极板电流和馈线电流的磁场
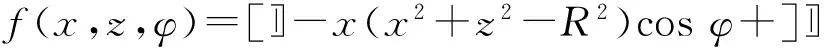
3 用全电流定律计算磁感应强度