RC分体柱应用于柔性隔震层最佳剪跨比研究
王松山,刘方成
(湖南工业大学 土木工程学院,湖南 株洲 412007)
RC分体柱应用于柔性隔震层最佳剪跨比研究
王松山,刘方成
(湖南工业大学 土木工程学院,湖南 株洲 412007)
为探究钢筋混凝土(RC)分体柱应用于柔性隔震层的最佳剪跨比,运用数值模拟对比研究整体柱和分体柱的延性系数、耗能系数和抗侧刚度。研究结果表明:分体柱与整体柱延性系数的比值随着剪跨比的增大而先增大后减小,且剪跨比在1.5~2.0范围内达到最大值;当<1.5时,分体柱与整体柱耗能系数比值随着剪跨比的增大而缓慢增大,但变化不明显,当≥1.5时,比值迅速增大;分体柱与整体柱抗侧刚度的比值随着剪跨比的增大而增大,剪跨比越大,分体柱越不利于隔震。综合得出最佳剪跨比范围为1.5~2.0。
分体柱;剪跨比;延性系数;耗能系数;抗侧刚度
0 引言
在汶川地震以及近期世界各地的多次地震中,以低、多层砌体或砖混结构为代表的刚性结构破坏比较严重[1-2]。究其原因,第一是低、多层房屋建设往往造价低,因此抗震措施落实不严;第二是低、多层结构的基本周期往往位于地震能量最大的周期范围之内,使得结构要承受很大的地震反应。基于地震反应谱原理,在此类刚性房屋底部设计一层柔性架空层,使原本刚度较大的低、多层房屋结构周期延长,使结构多地震影响大幅减小,从而起到隔震的效果。在建筑功能上,该柔性隔震层可不作为生命活动空间,比如在我国南方农村地区,可兼做防潮架空层及农具杂物室。为达到“大震不倒”的目的,要求该柔性隔震层具有较小的整体刚度和良好的延性。
分体柱的概念在20世纪80年代末被提出,是将整截面柱通过分隔缝划分为几个独立配筋的小单元柱(见图1),主要用于解决高层建筑中的短柱问题。胡庆昌等[3-8]对分体短柱的抗震性能进行了较深入的研究,得出分体柱在承载能力与整体柱相当的情况下,具有更好的变形和耗能能力,即延性显著改善。李亚萍[9]利用数值方法分析了分体柱在不同条件下的弹性抗侧刚度,结果表明,利用分体柱技术能够极大减小柱子的抗侧刚度,并显著增加柱子的延性。

图1 整体柱与分体柱截面Fig. 1 Cross sections of a monolithic column and split columns
根据分体柱刚度低、延性好的结构特点,可以采用其作为普通低、多层房屋结构的柔性隔震层,以延长结构的基本周期,降低上部结构对地震加速度的反应,达到隔震的目的。为研究分体柱用于隔震层的最佳柱子设计高度,需要研究分体柱在不同剪跨比下延性、耗能和抗侧刚度的表现。通过有限元分析钢筋混凝土整体柱和分体柱构件在不同剪跨比下的延性、耗能能力和抗侧刚度的差异,筛选出最佳剪跨比范围,以便为后续研究提供参考。
1 数值模型
1.1模型建立
整截面柱是截面尺寸为300 mm×300 mm的方柱,轴压比为0.6。相应的分体柱采用未设置过渡区的4个等截面单元柱,分隔缝宽度设置为10 mm,形成4个截面边长为145 mm的方形独立分体柱。对于整截面柱和分体柱,均设置尺寸为800 mm×250 mm× 500 mm的底面刚性基础和尺寸为300 mm×100 mm× 300 mm的刚性柱头。整体柱纵筋为1612,各单元柱纵筋为412,两者箍筋设置均为100@6,混凝土保护层厚度为20 mm。混凝土强度等级取为C30,抗压强度设计值为14.3 MPa,混凝土泊松比为0.2,纵向钢筋抗拉强度设计值为300 MPa,钢筋泊松比为0.3,弹性模量为2.0×105N/mm2。
1.2模型数值化
利用有限元软件ANSYS12.0对整体柱和分体柱进行受力分析。采用分离式钢筋混凝土模型,混凝土采用Solid65单元,钢筋采用Link8单元。刚性体柱头和基础采用Solid45单元。计算中采用以下基本假设:1)在低周反复荷载下,忽略各个分体柱之间节点的接触作用;2)忽略反复荷载作用下纵筋与混凝土之间的黏结滑移。混凝土本构模型采用GB50010—2010规定的单轴应力-应变曲线。采用多线性等向强化模型MISO及Willan-Warnker五参数破坏准则进行模拟,张开裂缝剪力传递系数为0.3,闭合裂缝剪力传递系数为0.9[10]。纵筋和箍筋采用双线性等向强化模型BISO。试件有限元模型如图2和图3所示。
图2 整体柱模型Fig. 2 A monolithic column model

图3 分体柱模型Fig. 3 A split column model
1.3工况分析
为研究剪跨比对分体柱侧移刚度的影响,设置了5组剪跨比(1.0~3.0),试件编号及设计参数如表1所示。数值分析时,按照轴压比为0.6在柱顶施加轴向荷载,采用如图4所示的加荷程序在柱顶施加低周反复水平荷载[11]。

表1 试件设计参数Table 1 Design parameters of specimens

图4 加载程序图Fig. 4 A loading program diagram
2 结果及分析
2.1滞回曲线

图5 不同剪跨比下整体柱的滞回曲线Fig. 5 Hysteretic curves for monolithic columns with different shear span ratios

图6 不同剪跨比下分体柱的滞回曲线Fig. 6 Hysteretic curves for split columns with different shear span ratios
2.2骨架曲线
根据整体柱和分体柱数值模拟每级循环的荷载-位移最大值,绘制出骨架曲线,如图7所示。

图7 不同剪跨比下整体柱与分体柱骨架曲线对比Fig. 7 A comparative diagram of skeleton curves between monolithic columns and split columns with different shear span ratios
由图7可以看出:在不同剪跨比下,整体柱弹性阶段的刚度明显高于分体柱,刚度退化不明显;随着位移的增加,进入塑性阶段,后期刚度逐渐退化。总体上,整体柱刚度高于分体柱。
整体柱和分体柱在各个剪跨比下的骨架曲线,分别如图8和图9所示。由图可知,整体柱和分体柱的刚度均随剪跨比的增大而减小,并且后期刚度变化较缓慢。

图8 整体柱骨架曲线Fig. 8 Skeleton curves for monolithic columns

图9 分体柱骨架曲线Fig. 9 Skeleton curves for split columns
2.3延性系数与耗能系数

式中:Δu为柱极限位移,定义为水平抗力到最大峰值抗力时的柱顶位移;
Δy为屈服位移,定义为最外层纵向钢筋初始屈服时对应的柱顶位移[12]。
结构的耗能能力可通过每次循环中荷载-位移滞回曲线所围面积的大小来反映,通常用耗能系数E来表征,如图10所示。


图10 耗能系数计算示意图Fig. 10 A calculation schematic diagram of the energy dissipation coefficient
通过数值模拟,可计算整理出整体柱与分体柱的延性系数和耗能系数,将两者的延性系数和耗能系数分别作对比,如图11和图12所示。
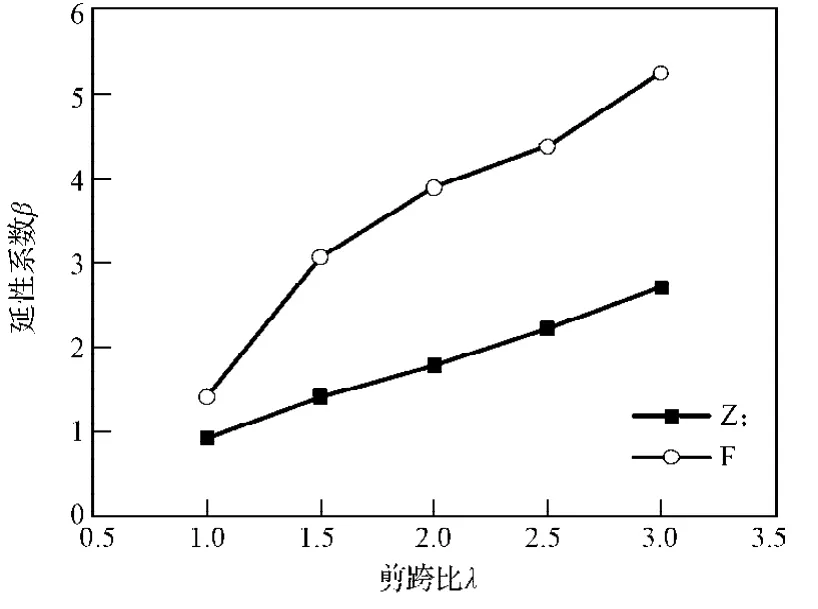
图11 整体柱与分体柱延性系数对比Fig. 11 A comparative diagram of the ductility coefficients between monolithic columns and split columns

图12 整体柱与分体柱耗能系数对比Fig. 12 A comparative diagram of the energy dissipation coefficients between monolithic columns and split columns
从图11和图12可以看出:在不同的剪跨比下,分体柱的延性系数明显高于整体柱相应的延性系数;分体柱的耗能系数整体高于整体柱的耗能系数,并且随着剪跨比的增大,整体柱的耗能系数下降较快,而分体柱仍能保持较大的耗能系数。
为了探究最佳剪跨比下分体柱的延性系数和耗能系数,将分体柱的延性系数、耗能系数分别与整体柱的作比值,其结果如图13所示。

图13 分体柱与整体柱延性系数以及耗能系数的比值Fig. 13 A comparative diagram of the ratios of the ductility coefficient and the energy dissipation coefficient between split columns and monolithic columns
由图可知:1)分体柱与整体柱的延性系数的比值总体大于1.5,且随着剪跨比增大呈先上升后下降的趋势,在为1.5~2.0时达到最大值2.2,在>2.0后略有下降,但最终仍大于1.8。2)分体柱与整体柱的耗能系数比值,在为1.0~1.5时约为1.0,当>1.5后迅速增大,直至=3.0时达到3.2左右,这说明随着剪跨比的不断增大,分体柱相对于整体柱的耗能能力增强。
综合比较分体柱与整体柱的延性系数和耗能系数,可得出分体柱用于柔性隔震时,其最佳设计剪跨比为1.5~2.0。
2.4抗侧刚度曲线
为了解分体柱和整体柱在不同剪跨比下的抗侧刚度的变化规律,取低周反复水平荷载作用下,正、反方向荷载(计算值)的绝对值之和,除以相应的正、反方向位移(计算值)绝对值之和,作为每级循环的平均刚度[8]。整体柱和分体柱抗侧刚度分别用KZ和KF表示。图14给出了整体柱和分体柱在不同剪跨比下的抗侧刚度曲线。由图可知,分体柱的抗侧刚度明显小于整体柱的抗侧刚度,尤其在剪跨比较小(≤1.5)时,分体柱的初始抗侧刚度远小于整体柱的。


图14 不同剪跨比下结构的抗侧刚度曲线Fig. 14 Lateral stiffness curves for structures with different shear span ratios
图15给出了分体柱与整体柱的抗侧刚度比值变化曲线。由图可知:1)在位移幅值不变的情况下,随着剪跨比的增大,两者抗侧刚度的比值整体呈增大趋势,当=3.0时,比值约为0.6。2)在剪跨比不变的情况下,随着位移幅值的增大,两者抗侧刚度的比值大体上呈先减小后增大的趋势。这说明分体柱在中等位移时具有更小的抗侧刚度,对于中震的隔震效果更好。

图15 分体柱与整体柱的抗侧刚度比值曲线Fig. 15 The ratio curves of the lateral stiffness between split columns and monolithic columns
3 结论
1)分体柱与整体柱延性系数比值随着剪跨比的增大而先增大后减小,在剪跨比为1.5~2.0时达到最大值,之后随着剪跨比的继续增大而略有下降。
3)分体柱与整体柱抗侧刚度比值随着剪跨比的增大而增大,当=2.0时,分体柱刚度约为整体柱刚度的0.4~0.6。剪跨比越大,采用分体方法获得的结构刚度降低程度减小,隔震效应降低。
4)钢筋混凝土分体柱应用于柔性隔震层最佳剪跨比范围为1.5~2.0。
[1]清华大学、西南交通大学、北京交通大学土木工程结构专家组. 汶川地震建筑震害分析[J]. 建筑结构学报,2008,29(4):1-9. Civil and Structural Groups of Tsinghua University,Xinan Jiaotong University and Beijing Jiaotong University. Analysis on Seismic Damage of Buildings in the Wenchuan Earthquake[J]. Journal of Building Structures,2008,29(4):1-9.
[2]曹万林,张勇波,董宏英,等. 村镇建筑抗震节能结构体系研究与应用[J]. 工程力学,2015,32(12):1-12. CAO Wanlin,ZHANG Yongbo,DONG Hongying,et al. Research and Application on Aseismic Energy-Saving Structural System for Rural Buildings[J]. Engineering Mechanics,2015,32(12):1-12.
[3]胡庆昌,徐云扉. 改善矩形截面钢筋混凝土短柱抗震性能的一个新途径[J]. 建筑科学,1989,5(3):3-8. HU Qingchang,XU Yunfei. A New Way for Improving the Seismic Behavior of Reinforced Concrete Short Columns[J]. Building Science,1989,5(3):3-8.
[4]郝永昶,胡庆昌,徐云扉,等. 应用分体柱改善短柱(高轴压比)抗震性能的试验研究[J]. 建筑结构学报,1998,19(6):2-11. HAO Yongchang,HU Qingchang,XU Yunfei,et al. Use of Separated Solumns to Improve the Seismic Behavior of Short Reinforced Concrete Columns[J]. Journal of Building Structures,1998,19(6):2-11.
[5]李忠献,郝永昶,张建宇,等. 钢筋混凝土分体柱框架梁柱中节点抗震性能的研究[J]. 建筑结构学报,2001, 22(4):55-60. LI Zhongxian,HAO Yongchang,ZHANG Jianyu,et al. Research on Seismic Behavior of Interior Beam-Column Joints of Reinforced Concrete Frames with Split Columns[J]. Journal of Building Structures,2001,22(4):55-60.
[6]李忠献,郝永昶,周兵,等. 钢筋混凝土分体柱框架抗震性能的模型试验研究[J]. 建筑结构学报,2003,24(6):1-10. LI Zhongxian,HAO Yongchang,ZHOU Bing,et al. Model Experimental Study on Seismic Behavior of Reinforced Concrete Frame with Split Columns[J]. Journal of Building Structures,2003,24(6):1-10.
[7]李忠献. 钢筋混凝土分体柱理论与技术[J]. 工程力学,2005,22(增刊1):127-141. LI Zhongxian. Theory and Technology of Split Reinforced Concrete Columns[J]. Engineering Mechanics,2005,22(S1):127-141.
[8]李忠献,代崇阳. 钢筋混凝土分体柱的抗震机理[J]. 地震工程与工程振动,2007,27(3):41-46. LI Zhongxian,DAI Chongyang. Seismic Mechanism of Reinforced Concrete Split Column[J]. Earthquake Engineering and Engineering Vibration,2007,27(3):44-46.
[9]李亚萍. 混凝土分体柱侧向刚度的简化计算[D]. 西安:长安大学,2012. LI Yaping. Simplified Calculation of Lateral Stiffness of Concrete Split Columns[D]. Xi'an:Chang'an University,2012.
[10]江见鲸,陆新征,叶列平. 混凝土结构有限元分析[M].北京:清华大学出版社,2005. JIANG Jianjing,LU Xinzheng,YE Lieping. Finite Element Analysis of Concrete Structures[M]. Beijing:Tsinghua University Press,2005.
[11]汪训流,陆新征,叶列平. 往复荷载下钢筋混凝土柱受力性能的数值模拟[J]. 工程力学,2007,24(12):76-81. WANG Xunliu,LU Xinzheng,YE Lieping. Numerical Simulation for the Hysteresis Behavior of RC Columns Under Cyclic Loads[J]. Engineering Mechanics,2007,24(12):76-81.
[12]韩林海,陶忠. 方钢管混凝土柱的延性系数[J]. 地震工程与工程振动,2000,20(4):56-65. HAN Linhai,TAO Zhong. Ductility Coefficient of Concrete Filled Steel Tubular Columns with Square Sections[J]. Earthquake Engineering and Engineering Vibration,2000,20(4):56-65.
(责任编辑:邓光辉)
On the Optimal Shear Span Ratio of RC Split Columns Applied to Flexible Isolation Layers
WANG Songshan,LIU Fangcheng
(School of Civil Engineering,Hunan University of Technology,Zhuzhou Hunan 412007,China)
In order to investigate the optimal shear span ratio of reinforced concrete (RC) columns applied to flexible isolation layers, a comparative analysis based on numerical simulation has been made of the ductility coefficient, the energy dissipation coefficient, and the lateral stiffness between monolithic columns and split columns. The results show that the ratios of the ductility coefficient between monolithic columns and split columns increase then decrease with the increase of its shear span ratios, with the maximum value of the latter achieved in the range of 1.5 to 2.0; when the shear span ratio is less than one point five, the ratios of the energy dissipation coefficient between monolithic columns and split columns increase slowly but not dramatically with the increase of its shear span ratios; when the shear span ratio is greater than or equal to one point five, the ratios of the energy dissipation coefficient between monolithic columns and split columns increase rapidly; the ratios of the lateral stiffness between monolithic columns and split columns increase with its shear span ratios,which are inversely proportional to the isolation effect. Thus, a final conclusion has been drawn: the optimal shear span ratio should be in the range of 1.5~2.0.
split columns;shear span ratio;ductility coefficient;energy dissipation coefficient;lateral stiffness
TU311.3
A
1673-9833(2016)03-0001-07
10.3969/j.issn.1673-9833.2016.03.001
2016-03-28
国家自然科学基金资助项目(51108177),湖南省自然科学基金资助项目(10JJ4040),湖南工业大学研究生科研创新基金资助项目(CX1410)
王松山(1990-),男,安徽滁州人,湖南工业大学硕士生,主要研究方向为结构隔震,E-mail:237960298@qq.com

