两二次曲线之间斜率关系结论发现的统一研究

赵临龙



两二次曲线之间斜率关系结论发现的统一研究

赵临龙

（安康学院数学与应用数学研究所，陕西安康 725000）

利用二次曲线的极点与极线关系，统一解决两二次曲线之间有关斜率关系的结论，揭示二次曲线之间斜率关系的内在本质.

二次曲线；极点；极线；斜率；关系；统一

1 问题背景

吴建山在文[1]中，研究2010年全国高中数学联赛试题江西省预赛试题，给出6个推广性质.

试题[1]给定椭圆C：2/22/2=1(>>0)，⊙：2+2=2，自椭圆上异于其顶点的任意一点P作⊙的2条切线，切点分别为M，N，若直线MN在轴上的截距分别为，，证明：2/22/2=2/2.

性质1[1]已知椭圆C1：2/2+2/2=1(>>0)和圆C2：2+2=2，过C1上一点P作C2的2条切线PM，PN（切点分别为M，N），则C1在点P处的切线斜率1与C2的切点弦MN的斜率2满足2122=0.

性质2[1]已知椭圆C1：2/22/2=1(>>0)和双曲线C2：2/22/2=1(>>0)，过C2上一点P作C1的2条切线PM，PN（切点分别为M，N），则C2在点P处的切线斜率1与C1的切点弦MN的斜率2满足1+2=0.

性质3[1]已知椭圆C1：2/22/2=1(>>0)和双曲线C2：2/22/2=1(>>0)，过C1上一点P作C2的2条切线PM，PN（切点分别为M，N），则C1在点P处的切线斜率1与C2的切点弦MN的斜率2满足1+2=0.

性质4[1]已知椭圆C1：2/22/2=1(>>0)和圆C2：2+2=2，过C2上一点P作C1的2条切线PM，PN（切点分别为M，N），则C1在点P处的切线斜率1与C2的切点弦MN的斜率2满足2122=0.

性质5[1]已知双曲线C1：2/22/2=1(>>0)和圆C2：2+2=2，过C1上一点P作C2的2条切线PM，PN（切点分别为M，N），则C1在点P处的切线斜率1与C2的切点弦MN的斜率2满足2122=0.

性质6[1]已知双曲线C1：2/22/2=1(>>0)和圆C2：2+2=2，过C2上一点P作C1的2条切线PM，PN（切点分别为M，N），则C1在点P处的切线斜率1与C2的切点弦MN的斜率2满足2122=0.我们说，射影几何的优势就是统一认识二次曲线的内在本质.因此，我们可以借促射影几何的二次曲线的“极点与极线”理论，统一来研究这些性质，揭示其内在本质.

2 理论准备

定义[2]过点P引二次曲线Γ的直线PAB交Γ于A、B两点，若直线PAB上一点Q满足：

则点Q轨迹为点P关于Γ的极线，点P为Γ的极点.

特例，二次曲线切点P的极线为过切点P与Γ相切的直线.

定理 过点P(x0，y0)引二次曲线Γ：

的直线PAB交Γ于A、B两点，若直线PAB上一点Q(x，y)满足(1)，则点Q轨迹为直线：

由（1）得：

于是，有结论（3）.定理获证.

推论1 二次曲线Γ上的极点P(x0，y0)的极线方程是（3）.

证明：在方程（3）中，反过来将点Q(x，y)看作极点，则极点Q关于二次曲线Γ的极线过点P(x0，y0).

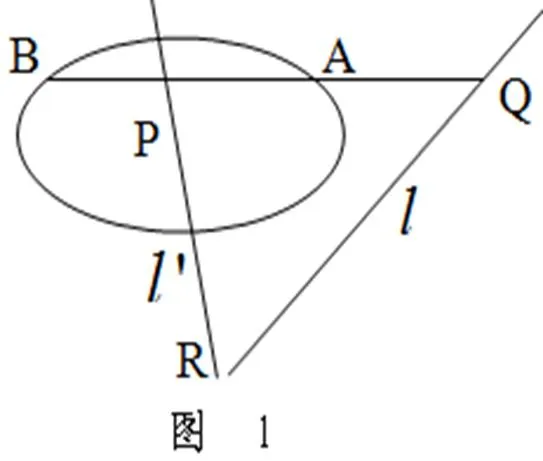
证明：如图1. 对于两极点P、Q，关于二次曲线Γ的极线分别是和，则和的交点R关于二次曲线Γ的极线分别过点P、Q，即直线PQ为极点R关于二次曲线Γ的极线.

推论4 过二次曲线Γ外一点P(x0，y0)引Γ的两切线PA、PB(A、B分别为切点)，则极点P的极线为AB，其极线方程形式为（3）.

证明：由于两极点A、B对应极线分别是PA和PB，则PA和PB的交点P关于Γ的极线为直线AB，其极线方程形式为（3）.

推论5 对于二次曲线Γ的极点P(0,0)的极线方程形式为：

3问题研究

3.1 性质的统一研究

性质7 已知椭圆Γ1：（）和双曲线Γ2：（），过Γ1（或Γ2）上一点P(x0，y0)（y0≠0）作另一条Γ2（或Γ1）的2条切线PM，PN（切点分别为M，N），则在点P处的切线斜率与切点弦MN的斜率满足.特例：当椭圆Γ1：（）退化为：时，.

特例当椭圆Γ1：（）退化为：时，斜率（y0≠0）；对于双曲线Γ2，斜率（y0≠0）.

显然，当y0= 0时，所得切线和切点弦均垂直于x轴，即k1和k2都不存在.因此，性质7中的条件“y0≠0”不能省略.这是文[1]忽略的地方，现在作以弥补.性质7将文[1]中的性质2、3、5、6统一起来。

性质8 已知椭圆Γ1：（）和Γ2：，过Γ1（或Γ2）上一点P(x0，y0)（y0≠0）作另一条Γ2（或Γ1）的2条切线PM，PN（切点分别为M，N），则在点P处的切线斜率与切点弦MN的斜率满足.

证明：对于椭圆Γ1，其极点P(x0，y0)（y0≠0）关于Γ1的极线（切线）方程为：，即斜率（y0≠0），极点P关于Γ2的极线（切点弦）方程为：（y0≠0）.于是；反之，对于圆Γ2，其极点P(x0，y0)（y0≠0）关于Γ2的极线（切线）方程为：（y0≠0），极点P关于Γ1的极线（切点弦）方程为：，即斜率（y0≠0）.于是，即结论成立.

同样，性质8中的条件“y0≠0”是对文[1]性质1和4的弥补（即将文[1]中的性质1、4统一起来），而且该结论与圆Γ2：的半径无关，即是对于文[1]性质1、4的推广.

3.2 新结论研究

性质9 已知抛物线Γ1：和椭圆Γ2：（），过Γ1（或Γ2）上一点P(x0，y0)（y0≠0）作另一条Γ2（或Γ1）的2条切线PM，PN（切点分别为M，N），则在点P处的切线斜率与切点弦MN的斜率满足.其中，对于抛物线Γ1上的点满足P(x0，y0)（），对于椭圆Γ2上的点P(x0，y0)满足.

证明：由Γ1和Γ2得交点坐标满足：，则.

反之，考虑点P(x0，y0)（-a<）在椭圆Γ2：（）上，由于点P关于曲线Γ1和Γ2的极线方程没有变化，即性质9结论依然成立.

4 研究启示

射影几何作为研究几何图形点线结合关系的重要学科，尤其对于二次曲线内在性质的统一性的认识，具有很强的指导作用.

4.1 统一命题

本文将文[1]中二次曲线的6个性质，统一为2个基本性质，并且扩充其内容，使结论形成更加完整的统一体，帮组人们认识问题的本质.

4.2 发现结论

本文进一步给出文[1]中二次曲线的抛物线相关性质，显示射影几何在几何发现中的独特作用，利于全面认识几何问题的内在本质.

有关射影几何的作用，还可参看笔者文献[3-6].

[1] 吴建山.一道高中数学联赛试题的探究与发现[J].中学教研（数学），2014（3）：48-49.

[2] 周振荣，赵临龙.高等几何[M].华中师范大学出版社，2013.

[3] 赵临龙，刘娟.射影几何对偶原理的优越性[J].重庆科技学院学报：自然科学版，2010（2）：176-177.

[4] 赵临龙.前我国初数研究存在的三种不良倾向——兼谈2003年北京市高考中的蝴蝶定理[J].重庆三峡学院学报，2013（3）：11-13.

[5] 赵临龙.初等数学研究途径：结构是基础 转化是关键——2012年高考数学北京理科第19题再探究[J].重庆三峡学院学报，2014（3）：11-13.

[6] 赵临龙.一道几何命题射影解法的启示[J].重庆三峡学院学报，2015（3）：18-20.

（责任编辑：涂正文）

A Unified Study of the Findings of the Slope Relationships Between Two Conic Curves

ZHAO Linlong

By using the relationships between the poles and the pole lines of conic curves, the paper aims to give a unified conclusion to all the slope-relationship findings between two conic curves, as well as to reveal the intrinsic essence of the slope relationship.

conic curve; pole; pole line; slope; relationship; unification

O182

A

1009-8135（2016）03-0005-04

2016-01-06

赵临龙（1960-），男，陕西西安人，安康学院三级教授，主要研究几何学.

陕西省特色专业建设项目（2011－59），安康学院重点学科建设项目（2013）阶段性成果