体外预应力简支梁动力特性的等效刚度分析法

王广利



体外预应力简支梁动力特性的等效刚度分析法

王广利

（黎明职业大学土木建筑工程学院，福建泉州 362000）

与已有假设相比，文章提出的2个主要假设更具合理性，计算结果更准确，与数值解能很好的吻合．计算表明：已有算法将体外筋对第1自振频率的效应作了较低估计，而对其他自振频率的效应作了较高估计；随体外筋面积和偏心距的增加，梁的第1自振频率也随之增加，其他频率保持不变．

体外预应力；简支梁；动力特性；等效刚度

目前，体外预应力结构研究较为深入的领域仅局限在其静力性能[1]，而对其动力性能的研究，尚无较为合理的定论，有待进一步研究．Ayaho Miyamoto[2]分析了体外预应力梁的动力性能，提出了体外筋预拉力增量与梁中点振动位移成正比的假设．熊学玉[3]等采用文献[2]提出的假设，推导出单折线型、双折线型和直线型体外筋简支梁自振频率的计算公式．在实验的基础上，熊辉霞[4]等改进了文献[3]给出的计算公式，使得计算结果与实验结果较吻合．方德平[5]提出了转向座与体外筋之间自由滑移无摩擦力和转向座与体外筋铰接无滑移两种方法，分析了体外预应力简支梁的动力性能，不过未给出相应的解析解．De-Ping Fang[6]应用能量法对体外预应力简支梁作了动力分析，给出了梁的自振频率的计算公式，但该公式不是真正意义上的解析解．体外筋预拉力增量与梁中点振动位移成正比是文献[2]和[3]中的一个核心假设．本文指出此假设中存在的问题，提出更具合理性的假设：在第1自振频率计算时，引入梁第1振型2阶导数的比例图，将体外筋预拉力增量导致的弯矩图视为与其等效，体外筋的效应体现为梁刚度的增加，体外预应力梁转化为具有等效刚度的受压梁；在其他自振频率计算时，略去体外筋的效应．本文的方法将体外筋的效应体现得更加明确，且概念清晰，推导过程简洁明了，计算结果与数值解能很好的吻合．为说明文献[2，3]假设中的问题，先回顾简支梁的弯曲振动微分方程．

1 弯曲振动微分方程

图1 转向座位于跨中的梁

式中，为梁的抗弯刚N体外预拉力，N为N的水平分量；为预拉力增量△N对梁的弯矩，=△N+△Nx，△N=△Ncosθ和△N=△Nsinθ，为锚固端处偏心距；为梁单位长度的质量．式(1)中，，水平预压力，为有效预应力，远小于；在式（6）中，由于与梁失稳临界压力F相比小很多，其产生的弯矩的作用很小，因而可将比作用更小的△Ny略去（文献[3]认为，与相比很小，所以△Ny远小于△Ne，因此可略去△Ny．由于偏心距可以为0，笔者觉得这并不合适），整理得：

需要建立2个关系：△N与的关系；△Nx与的关系，才能求解式（2）的微分方程．文献[3]假设梁中点的位移(0.5)与△N成正比：，即正比假设；通过跨中位移相等原则，把△Nx等效为△Nl/3；建立了2个关系，改写式（2）：

2(0.5)与△N成正比假设中存在的问题

在以上求解过程中所建立的△N与的关系，存在2个问题．问题（1）：对梁的第1振型而言，假设梁中点的位移(0.5)与△N成正比是合理的；可是在偶数振型中，(0.5)=0，假设(0.5)与△N成正比就不能成立；问题（2）：原假设△N与(0.5)成正比，△Nx与(0.5)/3成正比，为方便求解，在式（3）中，(0.5)被改写成．体外筋的△N与数值无关，而是的函数，这种改写不合理．在第1振型中，只有同号数值，如果这种改写尚可接受的话，那么在第2、3、4…振型中，有异号数值，这种改写将导致△N沿既有拉力又有压力，显而易见，这种改写不能成立．

3 弯曲振动分析的等效刚度法

对称简支梁的奇数振型为正对称，偶数振型为反对称．第2、4…偶数振型中，体外筋无变形，即△N=0，体外筋的效应无需考虑；第3、5…正对称振型中，梁的正负挠度产生的体外筋变形互相抵消[7]，总变形小，△N也小，因此△N的效应可略去．当体外筋的线形为sin(/)，偏心距=0，第3、5…振型X()=sin(/)，=3，5…产生的体外筋变形为∫X''sin(/)=0，则△N=0；体外筋的线形接近于抛物线或sin(/)，所以第3、5…振型产生的△N≈0．由此，本文假设：△N的效应只在第1振型中考虑，在其他振型中不考虑；在第1振型中，假设，即某一时刻，将的弯矩图等效为第1振型1()=sin(/)的2阶导数的比例图形，从而解决了(0.5)与△N成正比假设中的问题．的弯矩图与体外筋的线形成正比，体外筋的线形与第1振型相似，也与第1振型的2阶导数相似，所以这种等效是可行的．由此，式（1）改写为：（7）

本文作了3个假设：（1）体外筋的效应只是在第1自振频率计算时考虑，其他频率计算时忽略不计；（2）引入第1振型的2阶导数的比例图，将视为与其等效；（3） 略去△Ny的影响．本文的假设较(0.5)与△N成正比的假设相比，具有更强的合理性，因而计算结果更加准确．体外预应力梁在引入比例参数后，就可化为具有等效刚度*=+的普通混凝土受压梁，可体现体外筋对梁刚度的增强作用．在体外预应力梁跨中作用单位力1，产生的跨中位移△与等效刚度*梁的跨中位移相等，求出比例参数．

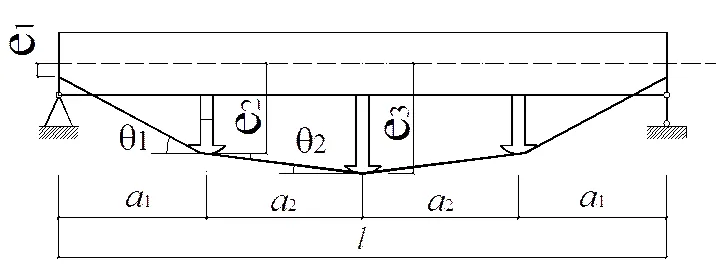
图2 体外预应力简支梁 图3 体外筋单位力作用时梁弯矩图m 图4 简支梁跨中单位力作用时弯矩图1

图2为体外预应力简支梁，为梁长，1，2为转向座的位置，1，2，3为体外筋的偏心距．跨中作用单位力1，体外筋的拉力，，，m为体外筋单位力作用下梁的弯矩图，如图3所示；1为梁跨中单位力作用下的弯矩图，如图4所示；11=1cos1，12=2cos1，21=2cos2，22=3cos2，1，2为体外筋的角度．，．由式（7），解得振动位移：=ΣX()sin(ωt+φ)，i=1，2，3… （8）

4 算例及分析

梁长=16 m、宽0.4 m、高0.8 m，=32.5GPa，单位长度质量=6 t/m；体外筋E=200 GPa、有效预应力σ=1000MPa，图2中1段与2段的水平预压力不同，取两段的平均值=0.5σA(cos1+cos2)；图2中1=2=4 m，1=0.2 m．表1为体外预应力梁第1、2、3自振频率的计算结果，8根计算梁考虑了不同偏心距、不同体外筋面积及不同体外筋线性，体外筋线形是双折线形（2=3）和近似抛物线形（2<3）．本文的计算结果是方法①；文献[3]的计算结果是方法②，在文献[3]中给出双折线形（2=3）计算公式，未给出近似抛物线形（2<3）的计算公式，表1也只列出方法②的双折线形计算结果；数值解是方法③．通常情况下，理论值的正确程度可用实验值来验证，但预应力梁中预拉力增大时，其实测的自振频率也增大，这与动力学中的结论相反．原因在于混凝土中的微裂缝在预压力作用下闭合，且预压力越大微裂缝的闭合越显著，增大了梁的刚度[4]．由此，在此问题中将理论值的正确性单纯的用实验值来验证是不合适的，因而本文采用数值解来进行验证．因转向座与体外筋之间自由滑移无摩擦力，体外筋整长的拉力相等．为了将这一滑移进行数值模拟，采用桁架单元模拟体外筋，在转向座两侧体外筋的角平分线上增加抗压的接触单元，也为桁架单元，这可确保两侧体外筋拉力相等[7]，如图5所示．本文中接触单元长度取1 cm，抗压刚度等于体外筋的抗拉刚度．集中质量法计算频率和振型时，对低阶的误差较小，对高阶的误差较大．对工程具有重要意义的是低阶的结果，尤其是1~3阶的结果，因而本文采用集中质量法对结构进行振动分析．集中质量法求解频率和振型的方程为：

[K]{}=2[]{} （9）

式中，[K]为梁的竖向刚度矩阵；[]为多质点质量对角矩阵，质点个数为；{}为某一振型，为对应的圆频率．如图6所示，给每个质点加竖向约束，在第质点处产生单位竖向位移，1~质点竖向约束的反力为；对1~各质点循环，求得竖向刚度矩阵[K]，用广义雅克比法求出个自振频率和振型．因而，混凝土梁的刚度和长度，体外筋的刚度EA和长度，转向座位置、高度，以及体外筋与转向座之间滑移均在图6质点处竖向约束反力中得到体现，也在式（9）刚度矩阵[K]中得到体现．

考虑压力对弯曲刚度的影响，梁的杆单元的弯曲刚度矩阵[]：

式中为轴力，以拉力为正．由式（10）可知，压力将减小梁的刚度，刚度减小，周期增大，自振频率将减少，即压缩软化效应．在方法③中，梁划分为16个等长杆单元，转向座处理为刚性单元．

表1 体外预应力梁第1～3自振频率的计算结果

表1中，①的1大于②的值，说明②将体外筋对1的效应作了较低估计．在②中，(0.5)被改写为，在位置，本应与最大值(0.5)成正比的△N降低为只与较小值()成正比，因而将体外筋的效应作了较低估计．对2而言，体外筋的拉力增量为零，①不考虑体外筋的作用；对3而言，①略去体外筋的作用；梁5~8的预压力大于梁1~4的预压力，所以梁5～8的频率略低于梁1~4的频率．②不适当地考虑了体外筋的效应，因此过高估计了2和3，所以方法①的2和3小于方法②的值．①和③的1很接近，说明①的合理与高精度．①和③的2相同，说明在偶数振型中，体外筋的应力增量为零，对自振频率没有作用．①和③的3也很接近，说明第3、5…振型中，梁的正负挠度产生的体外筋变形互相抵消，总的预拉力增量△N小，其效应可略去．由此可知，本文的假设是合理的，可得到高精度的计算结果．式（8）中F与2成正比，因而体外预应力筋对低阶的频率影响较大，对高阶的频率影响较小．表1中的值，即体外筋对梁刚度的增强作用，与体外筋的面积和转向座的高度成正相关．

5 结 论

（1）指出了体外预应力梁动力计算中体外筋预拉力增量与梁中点振动位移成正比这一假设中存在的2个问题，即该假设将体外筋对第1自振频率的效应作了较低估计，而对其他自振频率的效应作了较高估计．

（2）放弃了体外筋预拉力增量与梁中点振动位移成正比的假设．在第1自振频率计算中，引入梁第1振型2阶导数的比例图，将体外筋预拉力增量导致的弯矩图视为与其等效，体外筋的效应体现为梁刚度的增加，体外预应力梁转化为具有等效刚度的受压梁；在其他自振频率计算中，略去体外筋的效应．在体外筋的效应分析中，本文的概念清晰、精度高，且推导过程简洁明了，计算结果与数值解能很好的吻合．

（3）增加体外筋的面积，一方面体外筋的效应将提高，提高值，提高1；另一方面梁的压力将增大，降低1；由于前者的影响大于后者，增加体外筋的面积将提高梁的1．增大偏心距，体外筋的效应将提高，提高1．体外筋面积和偏心距不影响梁2阶及以上高阶的，但由于体外筋面积的增加，增大了梁的压力，略减少梁2阶及以上高阶的．

[1] 杜进生，区达光.体外预应力筋的极限应力：既有典型计算方法评述[J].工程力学，2010（9）：63-68.

[2] Ayaho Miyamoto, Katsuji Tei, Hideaki Nakamura, etal. Behavior of prestressed beam strengthened with external tendons [J].Journal of Structural Engineering, ASCE. 2000(9): 1033-1044.

[3] 熊学玉，王寿生.体外预应力梁振动特性的分析与研究[J].地震工程与工程振动，2005（2）：55-61.

[4] 熊辉霞，张耀庭.体外预应力混凝土梁自振频率分析[J].工程力学，2008，25（Supplement Ⅱ）：173-176.

[5] 方德平.体外预应力梁动力特性的两种数值分析方法[J].振动与冲击，2012（24）：168-171.

[6] De-Ping Fang．Second order effects of external prestress on frequencies of simply supported beam by energy method[J].Structural Engineering and Mechanics, 2014(4): 687-699 .

[7] 方德平，王全凤.体外预应力梁动力特性分析的一种新方法[J].地震工程与工程振动，2010（4）：66-71

（责任编辑：于开红）

Equivalent Stiffness Method for Analyzing Dynamic Behavior of External Prestressed Simple Beam

WANG Guangli

Comparing to the existing hypothesis, the two hypotheses proposed in this article are more reasonable, the calculation result is more accurate, and the goodness of fit to the numerical solution is higher. The calculation shows: the existing algorithm underestimates the external tendons effect on the beam’s first natural frequency and overestimates the external tendons effect on the natural frequency; with the increase of area of the external tendons and the eccentricity, the beam’s first natural frequency increases and the other natural frequency keeps invariant.

external prestress; simple beam; dynamic characteristics; equivalent stiffness

P315.92

A

1009-8135（2016）03-0092-05

2016-02-17

王广利（1975-），男，山东威海人，黎明职业大学副教授，主要研究建筑力学与结构应用．

福建省中青年教师教育科研社科A类项目（2014福建省高等学校教学改革研究专项）（项目编号：JAS14854）阶段性成果