证券市场指令流与收益的非线性依赖性研究:混合连接函数(Mixed Copula)在流动性及流动性黑洞问题上的应用
龚玉婷,徐信喆,杨朝军
证券市场指令流与收益的非线性依赖性研究:混合连接函数(Mixed Copula)在流动性及流动性黑洞问题上的应用
龚玉婷,徐信喆,杨朝军
(上海交通大学安泰经济与管理学院金融系,上海,200052)
高频环境下,研究流动性黑洞问题的关键在于理清净指令流与价格变化在极端情况下的动态关系。混合Copula能够帮助我们理解它们之间的非线性依赖关系。本文利用混合Copula模型,分别研究在一般状态下及发生持续的流动性冲击状态下,净指令流对收益的尾部依赖性(Tail Dependence)。研究表明,无论是沪深300指数,还是沪深300股指期货,净指令流与收益均存在明显的非线性依赖性,并且在极端情况下(发生流动性黑洞时)它们之间的非线性依赖性会发生很大的变化,并研究了股指期货推出前后,这种非线性依赖性的变化。研究表明,当沪深300股指期货推出后,沪深300指数净指令流与价格变化的尾部依赖性出现明显的非对称性,这很有可能是由于现货市场存在有限做空机制所引起的。文章进一步证实了指令簿信息对净指令流与收益的非线性依赖性具有一定的解释能力。我们建议在政策上,继续鼓励各单位落实融资融券及转融通业务,进一步加大其业务的推广范围,逐渐消除沪深300现货市场的净指令流与收益的尾部非对称依赖性,从而改善市场流动性。
流动性;流动性黑洞;连接函数
0 引言
Persaud提出了流动性黑洞理论用来解释金融市场瞬间崩塌现象,认为金融市场在短时间内骤然丧失流动性的一种现象称为流动性黑洞[1]。当金融机构从事市场交易时,由于投资组合、交易制度、风险控制等机制的同质化,在某一特殊情况下会引起对同一标的物进行相同的大量的相同方向的操作,如同时卖出某一证券组合,引起市场在瞬间全是卖出指令而买盘骤然消失,引起股价快速下跌,并且下跌带来更多的卖出指令,形成更大的下跌,即形成所谓的“流动性黑洞”。Morris和Shin之后又对之作了理论上的补充[2]。国内不乏学者对之进行了广泛和深入的研究,如姜建清和孙彬、马俐丽和顾金宏等[3-8]。
近几年,国内外金融市场突然暴跌事件时有发生,如2010年5月6日,道琼斯工业平均指数毫无征兆地不到30分钟时间里狂挫近千点,创造其历史最大单日跌幅,这是一次典型的流动性黑洞事件。大量的研究表明,暴跌与对市场流动性需求突然放大有关[9-13]:Chakravarty等认为在暴跌发生前30分钟,出现了大量的跨市场扫单(Intermarket Sweep Order,ISO)不平衡,而非扫单(Non-Sweep Order)并没出现显著的不平衡[11]。Easley等认为暴跌是由有毒指令流(Order Toxicity)引起的,并创建了VPIN指标来对有毒指令流进行测度[12]。无论是ISO不平衡理论,还是有毒指令流理论,其基本看法都是认为是对流动性的需求突然变大所导致的市场暴跌。因此,研究流动性黑洞问题的关键在于理清净指令流与价格变化在极端情况下的动态关系。已有文献对于两者的关系已有广泛而深入的研究[14-21],然而这些研究环境都是在一般均衡状态下进行的,由于缺乏计量方法,对于极端环境下的研究却并不多见。混合Copula 可以用于描述随机变量之间在上下尾部的非线性依赖性,因此能够帮助我们研究在极端情况下净指令流与价格变化的依赖关系。
本文采用混合Copula模型分别研究在一般状态下及发生持续的流动性冲击状态下,净指令流对收益的尾部依赖性(Tail Dependence),以及指令簿信息对净指令流与收益的非线性依赖性的解释能力。本文结构如下:第一部分对本文使用的数据分类方法、模型及估计方法加以阐述。第二部分对市场高频数据加以描述。第三部分首先研究在一般状态下,各市场净指令流与收益的尾部依赖性;随后定义流动性黑洞测度指标,研究在流动性黑洞发生时两者的尾部依赖性是如何变化的;最后研究了指令簿信息对于指令流与收益之间非线性关系的解释能力。第四部分给出结论及政策建议。
1 模型及方法
1.1 买卖指令流分类方法
基于量钟的采样方法(BVC,Bulk-Volume Classification)是相对于原来基于时钟的采样方法(Clock-Time Classification)而言的。在基于时钟的采样方法框架下,时间序列是按照时间等分进行采样的,即以等时间撮进行采样;而在基于量钟的采样方法框架下,时间序列是按照交易量等分来进行采样的,即每隔相等的交易量来进行采样,得到时间序列,其中是指第个采样点,是指第个量撮下最后一个时间撮所对应的下标。
在高频交易环境中,采用基于量钟的采样方法是研究高频数据比较常见的方法,如持续期模型(ACD、非对称ACD等)[22,23],主要是研究新息到达的频率,将等量成交量统计作为一个新息进行采样。采用基于量钟的采样方法具有以下几点好处:(1)在原有基于时钟的采样方法下,由于每个数据点所包含的交易量不同,因此每个数据点所包含的信息量也不同;而在基于量钟的采样方法下,每个数据点由于拥有相同的交易量,因此其所包含的信息量是相同的;(2)在基于时钟的采样方法下,如果采样频率过高,会产生不必要的噪音,如果采样频率过低,会忽略许多有用的交易信号[24]。而在基于量钟的采样方法下,由于每个采样点是等交易量(信息量)的,因此采样频率的影响可以忽略;(3)基于量钟的采样方法能够降低甚至消除时间序列本身的异方差特性,降低波动群聚效应的影响[25]。

(2)
(3)
表1 模型回归结果(BVC分类方法和L&R分类方法)

表1 模型回归结果(BVC分类方法和L&R分类方法)
BVC方法0.007*(0.004)1.694***(0.005) L&R方法-0.000(0.005)0.001(0.001)
注:参数下方括号内为对应的标准差。***、**、*分别表示在1%、5%、10%水平下显著。
可以看到,采用Lee和Ready的方法得到的净指令流与价格几乎完全无正向关系。而采用BVC方法可以很清楚的看到指令流与价格是正相关的,图1(a)和图1(b)给出了两种方法在不同时期净指令流与收益的关系图,从中也可以得到相同的结论。

(a) Lee和Ready 方法
(b) BVC方法
图1 收益与净指令流关系散点图
其次,本文测试了在不同的原始数据采样频率下,采用两种分类方法的稳健性。定义:为指令流不平衡,则,假设改变原始数据的采样频率,使采样频率是原来的倍,保持不变,则内的数据观测值的数量变为,此时

表2 不同数据频率对于OI的影响(=5000合约数)
(a) BVC方法

表2 不同数据频率对于OI的影响(=5000合约数)
数据频率加总后观测值均值方差最小值最大值 0.5秒/笔127892.2502.9459.99E-0659.479 1秒/笔127812.8493.2971.21E-0459.033 5秒/笔126272.9802.6954.01E-0459.576 10秒/笔124853.8334.3362.11E-0458.299 50秒/笔114673.2053.6114.71E-0463.191 100秒/笔101013.2493.595064.645

(b) L&R方法
综合以上两点,尽管缺乏直接方法来比较两种方法的优劣,但是通过间接的方法,我们认为BVC方法在高频环境下的分类结果要优于L&R方法,因此下文都将采用BVC方法来对数据进行采样。
1.2 流动性黑洞测度指标定义
本文认为,流动性黑洞的发生从微观结构上来说是由于发生了持续的流动性需求冲击(即指令流负冲击),从而在短期内导致做市商的逆向选择,使得流动性供给瞬间消失,从而造成价格暴跌的现象。因此,对于流动性黑洞测度指标的定义,也应从流动性需求冲击入手,本文定义:
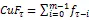
(6)

表3 不同m的取值对计算上下尾依赖性的影响
1.3 Copula模型及方法
Copula方法可以用于描述随机变量之间的非线性依赖性。Copula函数主要有椭圆族(elliptical)copula、阿基米德(Archimedean)copula等。关于copula函数的更多内容可参考Joe、Cherubini等、Nelson[29-31]。由于变量间可能同时具有上尾和下尾依赖性,而且这种尾部依赖性可能是不对称的[32,33]。为了更加灵活地反映变量间的相依结构,许多学者考虑对多个copula函数赋予不同的权重,进而得到混合copula模型[34-36]。此外,一些国内研究,如易文德、吴吉林和张二华,也用混合copula模型描述股市收益与成交量或各股市收益间的相依结构[37,38]。
为反映变量间上尾、下尾和中间部分不同的相依结构,我们以包含Clayton、Gumbel和正态(Gaussian)copula三种类型的混合copula为例进行说明。该混合copula的CDF可表示为:

(8)

(a) 沪深300股指期货()
(b)沪深300指数在股指期货推出前()(2009.01.01-2010.04.16)

(c)沪深300指数在股指期货推出后()(2010.04.16-2011.12.31)
(以0.5为界,的区域表示当净指令流和收益的累计分布函数都小于等于对应时的依赖性,的区域表示当净指令流和收益的累计分布函数都大于等于对应时的依赖性)
我们画出沪深300股指期货及现货指数的净指令流与收益在各分位点上的依赖性(如图2所示),可以清楚地看到,其上下尾部依赖性要明显小于中间的依赖性。沪深300股指期货上下尾部依赖性不存在明显的非对称性,而沪深300指数的上下尾部依赖性存在非常明显的非对称性(尤其是当沪深300股指期货推出后)。
2 数据描述
本文的数据来自国泰安CSMAR数据库,主要使用了如下数据:
(1)沪深300股指期货当月分笔高频5档数据,数据频率为0.5秒/笔,时间范围为2010年6月1日到2011年12月31日,跨度一年半。本文剔除了上午9:30之前及下午15:00之后的数据,旨在重点研究现货开市时间范围内的市场特征。同时,由于交割日附近当月合约与下月合约存在移仓现象,成交量显著减少,因此本文删除日交易量小于10万合约的临近交割日的数据。实际得到332天数据,共9307326个观测。

表4 沪深300股指当月期货及指数收益、成交量及成交金额统计信息
(2)沪深300指数分笔高频交易数据,数据频率为6秒/笔①,时间范围为2009年1月1日到2011年12月31日,历时三年②,实际得到,共2033164个观测,其中在2010年4月16日之前共有877102个观测,之后共有1156062个观测。
每笔数据的收益(Return)、成交量(Tickvol1)及成交金额(Tickvol2)的统计信息如表4所示,其中收益的单位为指数点,Tickvol1的单位为合约数,Tickvol2的单位为百万元。我们对收益、成交量、成交金额数据进行单位根检验,P值都小于0.01,表明变量都是平稳的。
3 实证结果及分析
3.1 净指令流与价格尾部依赖性研究
我们首先比较了混合copula与简单的正态copula对数据的拟合结果,研究表明采用混合copula模型要比简单的正态copula更能拟合数据(如表5(b)和表6(b)所示)。其次,使用不同的成交量规模(volbuck_size)可以得到类似的结果,说明分类方法具有很强的鲁棒性。
而且,如表5(a)和5(c)所示,股指期货净指令流与收益的高斯依赖性约为0.78,而上尾依赖性约为0.1,下尾依赖性约为0.04,上尾依赖性和下尾依赖性都远小于高斯依赖性,且下尾依赖性小于上尾依赖性。表明高频环境下,净指令流在极端情况下会对指令簿造成冲击,打破原来的流动性供给水平,流动性水平在短期内处于非均衡状态,且发生负极端情况下的净指令流对于指令簿的冲击程度要大于发生正极端情况下的净指令流对于指令簿的冲击程度。
沪深300指数同样存在类似的现象(如表6(a)和6(c)所示)。表6中,CSI300_1表示的是股指期货推出前的数据(2009.01.01-2010.4.15),CSI300_2表示的是股指期货推出后的数据(2010.04.16-2011.12.31)。在股指期货推出前,净指令流与收益的高斯依赖性约为0.86,而上尾依赖性和下为依赖性分别为0.28 和0.25,即上下尾部依赖性不存在明显的非对称性;而股指期货推出后,净指令流与收益的高斯依赖性约为0.89,而上尾依赖性和下为依赖性分别为0.28 和0.18,上尾依赖性基本不变,而下尾依赖性显著减小,上下尾部依赖性存在明显的非对称性。我们对同时期的上证50指数及中小板指数进行验证,并没有发现明显的非对称性(上证50指数的上尾和下尾依赖性分别为0.16和0.1;中小板指数的上尾依赖性和下尾依赖性分别为0.18和0.15)。在股指期货推出后,沪深300指数的下尾依赖性变小,对此有两种可能原因,其一从流动性供给的角度来讲,在极端情况下指令簿深度的波动加大,可能出现类似于Hasbrouck和Saar中所提到的“瞬逝单”的数量便大,造成流动性供给水平波动加大,导致净指令流对于收益的影响产生不确定性[39]。而高频交易者可能在其中扮演了主要的角色。其二是从流动性需求的角度来讲,在极端情况下净指令流的噪声变大,即在暴跌出现的瞬间,噪音交易者(即非知情交易者)的突然介入,打破了原来净指令流与价格的平衡。这部分交易者属于高频交易者,他们的介入减少了在暴跌过程中净指令流与价格的依赖性,对指令簿造成不可能预测的冲击。因此,无论从流动性供给的角度还是流动性需求的角度来讲,造成沪深300指数在股指期货推出后,净指令流对于收益在负极端情况下的依赖性减少的原因,很有可能是高频交易者的介入。而净指令流对于收益在正极端情况下的依赖性在股指期货推出前后并没有变化,说明市场缺乏做空机制。
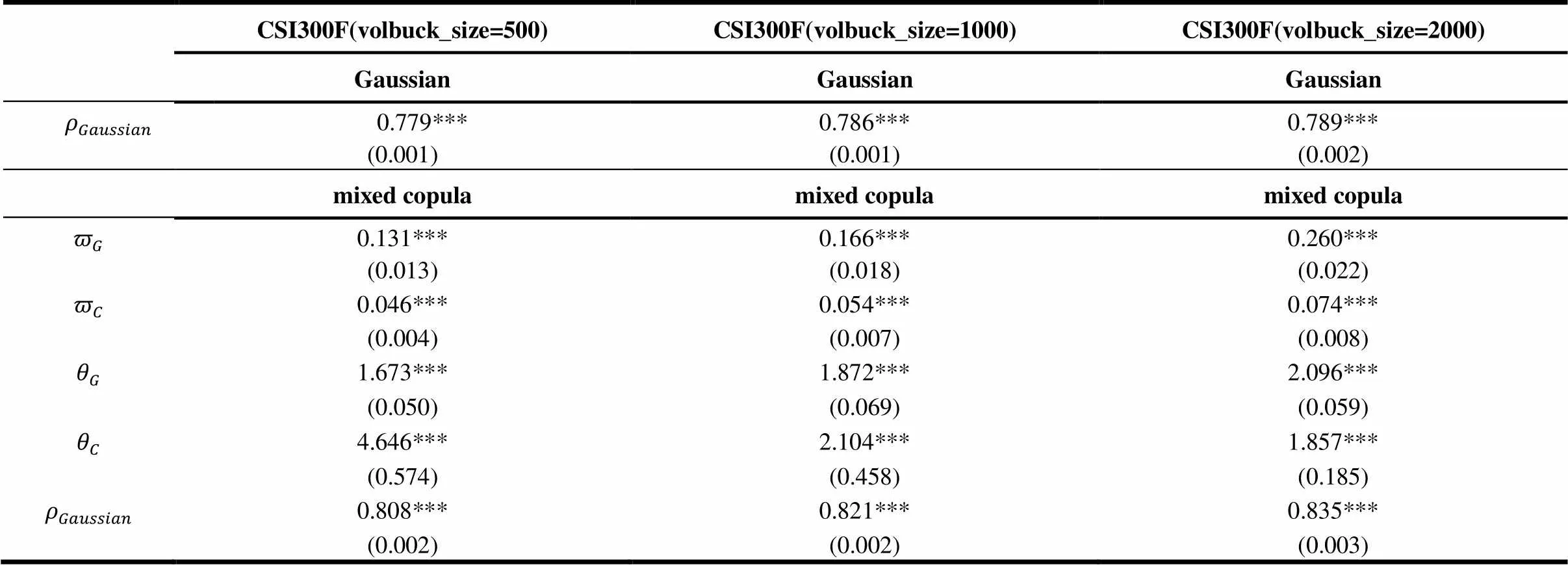
表5 沪深300股指期货Gaussian Copula和Mixed Copula回归结果(2009.06.01-2011.12.31)

(b) Gaussian Copula 和 Mixed Copula模型比较

(c) 上尾依赖性和下尾依赖性

表6 沪深300指数Gaussian Copula和Mixed Copula回归结果
注:参数下方括号内为对应的标准差。***、**、*分别表示在1%、5%、10%水平下显著。
表6(续)沪深300指数Gaussian Copula和Mixed Copula回归结果
(b) Gaussian Copula 和 Mixed Copula模型比较

CSI300_1(volbuck_size=300)CSI300_1(volbuck_size=500)CSI300_1(volbuck_size=1000) Gaussianmixed copulaGaussianmixed copulaGaussianmixed copula logL634086605448400510552855430417 AIC-126813-132097-96798-102101-57107-60824 BIC-126804-132050-96789-102056-57098-60782 CSI300_2(volbuck_size=300)CSI300_2(volbuck_size=500)CSI300_2(volbuck_size=1000) Gaussianmixed copulaGaussianmixed copulaGaussianmixed copula logL538915534139847414472279324029 AIC-107780-110672-79691-82884-45584-48048 BIC-107771-110625-79682-82839-45575-48007
(c) 上尾依赖性和下尾依赖性

CSI300_1(volbuck_size=300)CSI300_1(volbuck_size=500)CSI300_1(volbuck_size=1000) 上尾依赖性0.2540.2850.304 下尾依赖性0.2070.2490.288 CSI300_2(volbuck_size=300)CSI300_2(volbuck_size=500)CSI300_2(volbuck_size=1000) 上尾依赖性0.2380.2830.301 下尾依赖性0.1400.1820.226
3.2 流动性黑洞下的净指令流与价格尾部依赖性研究
上节中研究了证券市场净指令流与收益的尾部依赖性及其非对称性。然而,净指令流在短期内发生极端情况对市场的影响很可能是临时的,并不会产生持续的净指令流冲击,从而对证券市场造成持续的影响。本节研究当流动性黑洞发生时,净指令流与收益的尾部依赖性是如何变化的。
研究结论表明(如表7所示),沪深300股指期货在发生流动性黑洞和未发生流动性黑洞时,上尾依赖性和下尾依赖性并未发生显著变化。(发生流动性黑洞时的上下尾依赖性分别为0.07和0.04,未发生流动性黑洞时的上下尾依赖性分别为0.06和0.04(volbuck_size=500)。而沪深300指数在发生流动性黑洞时,上尾依赖性与未发生流动性黑洞时无显著变化,而下尾依赖性则相比于未发生流动醒黑洞时,要显著减小。(股指期货推出前,发生流动性黑洞时的上下尾依赖性分别为0.25和0.06,未发生流动性黑洞时的上下尾依赖性分别为0.24和0.23(volbuck_size=300),股指期货推出后,发生流动性黑洞时的上下尾依赖性分别为0.31和0.057,未发生流动性黑洞时的上下尾依赖性分别为0.22和0.15(volbuck_size=300)。

表7 沪深300股指期货在发生流动性黑洞时和未发生流动性黑洞时的尾部依赖性
这说明,在股指期货市场,发生流动性黑洞时与未发生流动性黑洞时的上下尾部依赖性均不存在显著的非对称性,这是由于期货市场可以进行双边交易;而在现货市场,发生流动性黑洞时,下尾依赖性则相比于未发生流动性黑洞时显著减小。说明当流动性黑洞发生时,卖方指令簿深度的波动并没有发生显著变化,而买方指令簿深度的波动增大,导致买方流动性供给水平遭到冲击。结合表5中的结论,可以发现,市场在一般状态下,即使偶然出现一两次大的净指令流冲击(流动性需求冲击),流动性供给的均衡水平并不会被打破,偶然的流动性需求冲击对于市场状态的影响是临时性的;只有当市场发生持续性的净指令流冲击后,其每次冲击的规模并不一定要求非常大,但其累计的量非常大,将对市场流动性供给水平造成显著的冲击,造成隐形做市商的逆向选择问题,从而导致市场进入一个非均衡的混沌状态,净指令流与收益在尾部的关联性均衡被打破。
3.3 加入指令簿信息后,净指令流与价格尾部依赖性研究
指令簿信息对研究投资者的交易行为有着深厚的意义,Biais利用实证数据较早研究指令流不平衡与价格关系,通过巴黎交易所数据,发现较薄的指令簿会引出更多的指令,而较厚的指令簿会导致交易[40]。为了争取价格和时间,当价差较大时,交易者更加倾向于挂单在报价单当中的价格,并且,当买(卖)大单发生时,买卖报价单都会朝买(卖)方大单的方向变动。Pascual和Veredas通过对西班牙股市交易数据研究发现,最佳报价单(best quotes)深度能够更好地解释交易者的激进程度,而非最佳报价单(the book beyond the best quotes)对交易者的激进程度也有一定的解释力[41]。Deuskar和Johnson研究了指令簿逆斜率对于由指令流驱动的风险比例、的影响,研究表明未考虑指令簿逆斜率因素时,由指令流驱动的风险比例大约20%,而考虑了指令簿逆斜率因素后,由指令流驱动的风险占到了整个价格风险的50%[42]。
在指令流驱动的市场中,指令簿信息反映了目前市场上,某证券标的物在某些价格下的供需状态,是一类流动性指标构建的来源。另一方面,我们知道,净指令流对于价格的作用可以表达为:,其中是收益,是净指令流,是误差项。从图1(b)的沪深300股指期货净指令流与收益的散点关系图中可以看到,其二者的关系并非完全线性,散点图呈现一个平行四边形的形状,因此,参数并非常量,而是时变的。这主要是由于指令簿状态在每一时刻都会发生变化,其变化反映了该证券标的物的供需变化,买卖指令簿逆斜率(ILOBS,Inverse Limit Order Book Slope)反映了当前单位量的净买入或者净卖出可以引起价格多大的变化,因此是参数的一个代理变量。在高频环境下,如果将净指令流乘以指令簿逆斜率后()对于的解释力变大,则说明净指令流和收益之间的非线性关系的一部分原因可以被指令簿逆斜率所解释。并且,由于可以更快的被观察到,因此可将它作为高频环境下的流动性测度水平指标。Deuskar和Johnson也进行过类似的研究,但只在线性回归的框架下[42]。

我们画出净指令流乘以指令簿逆斜率后,与收益的散点关系图(如图4(b)所示)。从直观上来看,净指令流乘以指令簿逆斜率后,其与价格的散点图呈现更加明显的线性关系,说明其对价格的解释能力均有一定程度的增强。

(a) Netflow与Return
(b) Netflow*ILOBS_D与Return
图4 净指令流乘以指令簿逆斜率后与收益的散点关系图

表8 考虑指令簿逆斜率的沪深300股指期货Gaussian Copula和Mixed Copula回归结果(2010.06.01-2011.12.31,volbuck_Size=500)
注:参数下方括号内为对应的标准差。***、**、*分别表示在1%、5%、10%水平下显著。
表8列出了指令簿逆斜率乘以净指令流后与收益的依赖性的统计结果(Return v.s. ILOBS_D*Netflow),并同时给出净指令流与收益的统计结果(Return v.s. Netflow)。可以看到,收益与净指令流的高斯依赖性为0.78,其上下尾部依赖性仅有0.06和0.04。而当净指令流乘以指令簿逆斜率后,其与收益的高斯依赖性分别上升的到了0.95,而其上下尾部依赖性也分别上升到了0.26和0.27。表明指令簿逆斜率确实能够增加净指令流对于价格的解释能力,净指令流与价格之间的非线性关系很大程度上是由指令簿逆斜率的变化所造成的,说明指令簿确实可以作为高频环境下的流动性指标测度。类似于3.2节,我们将数据分成发生流动性黑洞时和未发生流动性黑洞时两种状态,在两种状态下,都可以得到类似的结果(如表8(c)所示)。
表8(续)考虑指令簿逆斜率的沪深300股指期货Gaussian Copula和Mixed Copula回归结果(2010.06.01-2011.12.31,volbuck_Size=500)
(b) Gaussian Copula 和 Mixed Copula模型比较

Return v.s. Netflow Gaussianmixed copula logL59042.6logL59746.74 AIC-118083AIC-119483 BIC-118073BIC-119435 Return v.s. ILOBS_D*Netflow Gaussianmixed copula logL78412logL83091.91 AIC-156822AIC-166174 BIC-156813BIC-166128
(c) 上尾依赖性和下尾依赖性
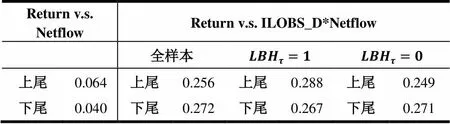
Return v.s. NetflowReturn v.s. ILOBS_D*Netflow 全样本 上尾0.064上尾0.256上尾0.288上尾0.249 下尾0.040下尾0.272下尾0.267下尾0.271
3.4 我国资本市场产生流动性黑洞的原因分析
从3.2和3.3节中的实证可以看出,市场发生流动性黑洞时净指令流与价格之间原有的依赖关系被打破,流动性的供需平衡遭到破坏,在短期内形成呈现一种无序的状态,流动性骤然消失,价格的波动放大,即使很小的买单或者卖单,都有可能引起价格剧烈变化,这样的现象被称为“流动性黑洞”。
产生流动性黑洞现象的原因有很多,这里仅讨论高频环境下的形成原因。在一个证券市场中,为分析简便,我们把交易者简单地分为知情交易者和非知情交易者,知情交易者根据价格的真实信息进行交易,而非知情交易者根据市场状况(价格信息和指令流信息)进行交易。在高频环境下,我们又可以把非知情交易者分为非知情的普通交易者和非知情的高频交易者,非知情的普通交易者不会立刻对市场状态信息做出反应,而非知情的高频交易者则会对市场当前的状态立刻做出交易决策。此时,在短期内可以忽略非知情的普通交易者对市场的影响。因此,对股价可能产生影响的就是知情交易者和高频交易者。我们可以把流动性黑洞发生的原因根据交易者的类型不同简单的归为两类,一类是知情交易者所引起的流动性黑洞,另一类是非知情交易者所引起的流动性黑洞。在我国,由于存在较强的信息不对称因素,因此,知情交易者一旦发现外部信息冲击,就会试图通过交易来获得超额收益。此时,流动性黑洞是由于外部冲击所引起的。除此之外,由于高频交易者的介入,其投资组合、交易制度、风险控制等机制的同质化,在某一特殊情况下引起对同一标的物进行相同的大量的相同方向的操作,如同时卖出某一证券组合,引起市场在瞬间全是卖出指令而买盘骤然消失,引起股价快速下跌,并且下跌带来更多的卖出指令,形成更大的下跌,即形成所谓的“流动性黑洞”[1]。此时的流动性黑洞并非由外部信息冲击造成,而是由内部流动性需求冲击所导致的。由内部流动性需求冲击所导致的流动性黑洞现象,可以用行为金融学中的投资者行为来解释。

图5 流动性黑洞形成原因示意图
4 结论及政策建议
本文采用A股市场的高频分时数据,首先使用Easley等提出的BVC方法对买卖指令流进行分类,随后采用混合Copula模型,分别研究在一般状态下及流动性黑洞发生状态下,净指令流对价格变化的尾部依赖性(Tail Dependence)[25]。研究表明,各市场的上尾依赖性和下尾依赖性都远小于高斯依赖性,股指期货的上下尾依赖性无显著差别,而沪深300指数的净指令流与收益的下尾依赖性在股指期货推出后显著变小,说明在极端情况下流动性供给的波动变大或者流动性需求的波动变大,很有可能是高频交易者的突然介入所导致的;而净指令流对于收益的上尾依赖性在股指期货推出前后并没有变化,说明市场缺乏有效的做空机制。2012年8月27日,经中国证监会批准,中国证券金融公司发布《转融通业务规则》和《融资融券业务统计与监控规则》,上海证券交易所、深圳证券交易所和中国证券登记结算公司同日也发布了转融通业务配套细则,标志着转融通试点实质启动。
最近三年A股市场融资融券规模如表9所示。目前来说,融资融券总规模三年放大近10倍,其业务渗透率不断加大。然而,融资余额与融券余额的规模仍然呈现较强的非对称性(目前融资余额超过融券余额十倍),“无券可融”仍然是目前融资融券业务的主要问题,通过进一步放开转融通业务的准入门槛有助于解决目前“无券可融”的尴尬情况。此外,手续费用过高也是限制融资融券业务开展的主要因素,目前进行融券交易的手续费高达9%,这种不合理的定价水平很大程度上造成了投资者意愿不强烈的现状。我们建议在政策上,继续鼓励各单位落实融资融券及转融通业务,进一步加大其业务的推广范围,降低准入门槛,逐渐消除沪深300现货市场的净指令流与收益的尾部非称依赖性,从而改善市场流动性。

表9 2011年至2013年融资融券规模
本文随后将市场状态划分为发生流动性黑洞时和未发生流动性黑洞时的两种状态。研究表明,市场在一般状态下,即使偶然出现一两次大的净指令流冲击(流动性需求冲击),流动性供给的均衡水平并不会被打破,偶然的流动性需求冲击对于市场状态的影响是临时性的;只有当市场发生持续性的净指令流冲击后,将对市场流动性供给水平造成显著的影响,造成隐形做市商的逆向选择问题,从而导致市场进入一个非均衡的混沌状态,净指令流与收益在尾部的关联性被打破。本文进一步证实了指令簿逆斜率对净指令流与收益的非线性依赖性具有一定的解释能力,表明指令簿逆斜率在高频环境下是一个很好的流动性代理变量。
[1] Persaud AD. Liquidity black holes [J]. Risk, 2003.
[2] Morris S, Shin SH. Liquidity black holes [J]. Review of Finance, 2004. 8(1): 1-18.
[3] 姜建清, 孙彬. 重建市场信心是缓解流动性危机的有效途径[J]. 金融论坛, 2009(1): 5-11.
[4] 马俐丽, 顾金宏. 中国银行间国债市场流动性黑洞的实证检验[J]. 金融论坛, 2010(4): 21-25.
[5] 李援亚. 流动性黑洞问题研究[J]. 财会月刊: 理论版, 2008(4): 26-28.
[6] 陈灯塔, 周颖刚. 理性恐慌, 流动性黑洞和国有股减持之谜[J]. 经济学, 2006. 5(2): 379-402.
[7] 孙彬. 金融危机中流动性黑洞问题研究[博士学位论文]. 上海交通大学, 2010.
[8] 孙彬, 杨朝军, 于静. Copula 函数选择对投资组合压力测试的影响分析[J]. 管理科学, 2009(2): 99-105.
[9] Madhavan A. Exchange-Traded Funds, Market Structure, and the Flash Crash [J]. Financial Analysts Journal, 2012, 68(4): 20-35.
[10] Kirilenko A, Kyle AS, Samadi M,., The flash crash: The impact of high frequency trading on an electronic market [C]. Working paper, University of Maryland, 2010.
[11] Chakravarty S, Upson J, Wood R. The flash crash: trading aggressiveness, liquidity supply, and the impact of intermarket sweep orders [C]. Working paper, University of Texas at El Paso, El Paso, TX, 2010.
[12] Easley D, De Prado ML, O’Hara M. The exchange of flow toxicity [J]. The Journal of Trading, 2011, 6(2): 8-13.
[13] Easley D, De Prado ML, O’Hara M. The microstructure of the flash crash: Flow toxicity, liquidity crashes and the probability of informed trading [J]. Journal of Portfolio Management, 2011, 37(2): 118-128.
[14] Biais B, Weill PO. 2009. Liquidity shocks and order book dynamics [R]. National Bureau of Economic Research, 2009.
[15] Brown P, Walsh D, Yuen A. The interaction between order imbalance and stock price [J]. Pacific-Basin Finance Journal, 1997, 5(5): 539-557.
[16] Chan K, Fong WM. Trade size, order imbalance, and the volatility-volume relation [J]. Journal of Financial Economics, 2000, 57(2): 247-273.
[17] Chordia T, Roll R, Subrahmanyam A. Order imbalance, liquidity, and market returns [J]. Journal of Financial Economics, 2002, 65(1): 111-130.
[18] Chordia T, Subrahmanyam A. Order imbalance and individual stock returns: Theory and evidence [J]. Journal of Financial Economics, 2004, 72(3): 485-518.
[19] Lee C, Ready MJ. Inferring trade direction from intraday data [J]. The Journal of Finance, 1991, 46(2): 733-746.
[20] Parlour CA. Price dynamics in limit order markets [J]. Review of Financial Studies, 1998, 11(4): 789-816.
[21] Pascual R, Veredas D. What pieces of limit order book information matter in explaining order choice by patient and impatient traders? [J]. Quantitative Finance, 2009, 9(5): 527-545.
[22] Engle RF, Russell J R. Autoregressive conditional duration: a new model for irregularly spaced transaction data [J]. Econometrica, 1998: 1127-1162.
[23] Bauwens L, Giot P. Asymmetric ACD models: introducing price information in ACD models with a two state transition model [C]. Working paper, Universite catholique de Louvain, Center for Operations Research and Econometrics (CORE), 1998.
[24] Engle RF, Lange J. Predicting VNET: A model of the dynamics of market depth [J]. Journal of financial Markets, 2001, 4(2): 113-142.
[25] Easley D, Lopez de Prado M, O’Hara M. Measuring flow toxicity in a high frequency world [C]. Working paper, Cornell University, 2010.
[26] Easley D, Lopez de Prado M, O'Hara M. Bulk Classification of Trading Activity [C]. Johnson School Research Paper Series, 2013,(8).
[27] Shenoy C, Zhang YJ. Order imbalance and stock returns: Evidence from China [J]. The Quarterly Review of Economics and Finance, 2007, 47(5): 637-650.
[28] Fung JK, Yu PL. Order imbalance and the dynamics of index and futures prices [J]. Journal of Futures Markets, 2007, 27(12): 1129-1157.
[29] Joe H. Multivariate models and multivariate dependence concepts [M]: Chapman & Hall/CRC, 1997.
[30] Cherubini U, Luciano E, Vecchiato W. Copula methods in finance [M]: Wiley, 2004.
[31] Nelsen RB. An introduction to copulas [M]: Springer Verlag, 2006.
[32] Ang A, Chen J. Asymmetric correlations of equity portfolios [J]. Journal of Financial Economics, 2002, 63(3): 443-494.
[33] Gong YT, Zheng X. Asymmetric dependence in stock returns based on copula-EGARCH models [C]. Working paper, Shanghai Jiaotong University, 2012.
[34] Hu L. Dependence patterns across financial markets: a mixed copula approach [J]. Applied Financial Economics, 2006, 16(10): 717-729.
[35] Chen X, Fan Y. Estimation and model selection of semiparametric copula-based multivariate dynamic models under copula misspecification [J]. Journal of Econometrics, 2006, 135(1): 125-154.
[36] Hong Y, Tu J, Zhou G. Asymmetries in stock returns: Statistical tests and economic evaluation [J]. Review of Financial Studies, 2007, 20(5): 1547-1581.
[37] 易文德. 基于 Copula 函数模型的股市交易量与股价相依关系[J]. 系统工程, 2010, 28(10): 36-41.
[38] 吴吉林, 张二华. 基于机制转换混合 Copula 模型的我国股市间极值相依性[J]. 系统工程理论与实践, 2012, 32(8): 1662-1672.
[39] Hasbrouck J, Saar G. Technology and liquidity provision: The blurring of traditional definitions [J]. Journal of Financial Markets, 2009, 12(2): 143-172.
[40] Biais B, Hillion P, Spatt C. An empirical analysis of the limit order book and the order flow in the Paris Bourse [J]. The Journal of Finance, 1995, 50(5): 1655-1689.
[41] Pascual R, Veredas D. What pieces of limit order book information do are informative? an empirical analysis of a pure order-driven market [C]. SSRN Working paper, 2003.
[42] Deuskar P, Johnson TC. Market liquidity and flow-driven risk [J]. Review of Financial Studies, 2011, 24(3): 721-753
Nonlinear Dependence of Order Flow and Return on Stock Market:Applying Mixed Copula in the problem of Liquidity and Liquidity black hole
XU Xin-zhe, GONG, Yu-ting, YANG Chao-jun
(Antai College of Economics & Management, Shanghai Jiaotong University, Shanghai 200052, China)
The relationship between net order flow and price change is the key to studying the problem of liquidity black hole. Mixed copula methods can help us understand the nonlinear dependence between them. In this paper, we use the BVC method proposed by Easley et al. to classify the buy and sell orders and verify its effectiveness. Based on the BVC method, net order flows and price change exhibit significantly positive dependence, and the order imbalance measure is stable under different sampling frequencies.First, in section 3.1, we apply the mixed copula model for the first time in studying the tail dependence between the net order flow and return. Studies have shown that in both CSI300 Index spot and futures markets, net order flow and return have a significant non-linear relationship. Their tail dependence is much smaller than their Gaussian dependence, which means that the net order flow in extreme cases will break the balance of liquidity supply level. The underlying market shows asymmetry in tail dependence after the launch of the CSI 300 Index Futures. This may attribute to the involvement of high frequency traders, and the lack of short-mechanism on underlying market. Second, in section 3.2, we further study the tail dependence between net order flow and return both in usual time and in ‘liquidity black hole’ environment. In CSI300 Index market, when liquidity black hole happens, which means the market is suffered from persistent negative order flow shocks, the lower-tail dependence between net order flow and price is much smaller than the upper-tail dependence. However, it is not the case when liquidity black hole does not happen. This shows that occasional order flow shocks would not break the balance of liquidity supply level. However, persistent order flow shocks would break their balance. Third, in section 3.3, we continue to investigate whether the order book information can explain the nonlinear relationship between net order flow and return. Results have shown the inverse limit order book slope can partly explain the nonlinear dependence between net order flow and return. Most of the nonlinear dependence is caused by the changes in inverse limit order book slope.Last, in section 3.4, we discuss the causes of liquidity black hole under high-frequency environment in Chinese stock market. Based on the types of market traders, liquidity black hole can happen due to two reasons: exogenous information shocks from information traders and endogenous liquidity demand shocks from noise traders.Overall, from the empirical analysis, we recommend that it is necessary to encourage the implementation of margin financing and refinancing business, and further increase the scope of the business to gradually eliminate the asymmetric tail dependence of net order flow and return on CSI 300 stock market, thereby improving market liquidity.
liquidity; liquidity black hole; copula function
中文编辑:杜 健;英文编辑:Charlie C. Chen
F273
A
1004-6062(2016)03-0151-10
10.13587/j.cnki.jieem.2016.03.019
2013-07-29
2014-04-25
国家自然科学基金资助项目(71273170)
龚玉婷(1985—),女,福建宁德人,上海交通大学,博士生,研究方向:金融计量。
①尽管沪深300股指期货数据和沪深300指数数据的采样频率存在较大差异(沪深300股指期货数据的频率为0.5秒每笔,而沪深300指数数据的频率为6秒每笔),但由于采用了BVC方法,该方法固定成交量(沪深300股指期货是每500份合约,沪深300指数是每300百万元成交金额)内对买卖指令流进行加总分类,加总后的数据消除了频率的影响(加总后的数据沪深300股指期货平均每日约350个观测数据,沪深300指数平均每日约280个观测数据)。
②沪深300股指期货数据时间跨度为一年半,而沪深300指数数据跨度为三年,目的是为了研究沪深300指数在股指期货推出前后的非对称效应,后面结论表明在沪深300股指期货推出前指数市场净值令流对于价格不存在明显的非对称效应,而在沪深300股指期货推出后,指数市场存在明显的非对称效应。

