公共信息、内部启发性对监管市场均衡的影响
张铁红,周永辉
(1.贵州师范大学 数学科学学院,贵州 贵阳 550001;2.贵州师范大学 大数据与计算机科学学院,贵州 贵阳 550001)
0 引言
在经济社会中内部交易普遍存在,内部交易者常常利用自己的私有信息优势获取利润。kyle[1]首先提出了内部交易的数学模型,并在半强有效性定价下,得到了单个内部交易者以噪声交易者为掩护而获取最优期望利润。在此基础上,Holden和Subrahmanyam[2]分析了多个内部交易者的博弈模型,并表明会加快信息释放的速度。进一步Gong等[3]对内部交易Stakelberg博弈模型进行了分析。Yang等[4]研究了内部交易市场中有新进者的Stakelberg博弈模型,并发现第一阶段市场价格波动是正相关,而二阶段却为负相关。另外,Zhao等[5]分析了定价准则公开性对内部交易均衡的影响等。
事实上,内部交易者利用私人信息获取利润,在一定程度上损害了噪声交易者的利益。1934年,美国国会颁布《证券交易法案》对内部交易者进行限制。之后,1984年《制裁法》和1988年《内幕交易和证券交易法》中要求:内部交易者如果获取利润超过三倍以上,则要接受处罚[10]。后来,Bhattacharya 和Spiegel[6]从理论上证明了内部交易监管的必要性。Shin[7]进一步提出测量监管力度的指标,并指出市场专家数量和信息的精度对最优监管政策的影响。另外,Luo[8]还建立了当内部交易者和做市商同时收到公共信息时的内部交易均衡模型,指出公共信息对内部交易者不利而噪声交易者有利。之后,唐齐鸣等[9]采用Shin提出的监管力度,当噪声交易者损失最小时,得出了一类内部交易市场的最优监管力度和交易策略。进一步,Liu等[10]基于Shin[7]提出的监管函数,研究了当理性内部交易者和启发性内部交易者等参与交易时的最优监管。
注意,不同市场代理人收到的信息及认识信息的程度往往有一定差别,从而产生了信息对内部交易影响的研究。Jain等[11]建立了做市商接收到部分风险资产信息的内部交易模型。此外,Fischer等[12]研究了对信息反应过度的启发性内部交易者和贝叶斯内部交易者参与市场的内部交易模型。Zhou[14]研究了不同自信程度下的内部交易博弈模型。Liu等[14]指出过度自信内部交易者、理性内部交易者及启发性内部交易者可以共存,获取各自利润。其它关于部分信息的内部交易研究见[14-19]等。
内部交易市场往往是复杂的,不同代理人收到关于风险资产的信息,内部交易者要追求利润最大化,做市商要进行公平定价,市场监管要保证噪声交易者的利益等等。基于以上文献,将研究具有市场监管与公共信息的内部交易市场中的最优内部交易策略、有效性定价以及最优监管所组成的均衡及其特征。
1 模型
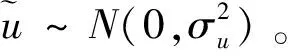
(1)
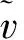
(2)

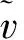

下面给出该市场均衡的定义。
2 Bayesian-Nash均衡
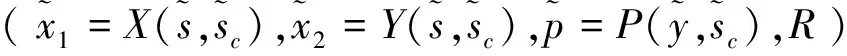
1)利润最大化
理性内部交易者利润最大化:给定Y、R和P,对任意的交易策略X'有
启发性内部交易者利润最大化:给定X、R和P,对于任意的交易策略Y'有
2)市场定价的有效性:给定X、Y和R
3)最优监管:给定X、Y和P

(3)

3 主要结果
现在,我们给出上述内部交易模型线性均衡的存在性与唯一性定理。
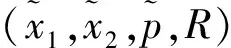
其中,

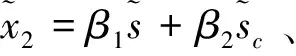
由极值的一阶导数条件,有
又由等式(1):
故有
(4)
由极值二阶导数小于零的条件,有λ+R>0。
结合等式 (3)和 (4),得到
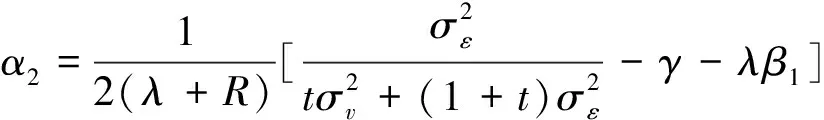
由极值的一阶导数条件,有
又因为启发性内部交易者过于看重当前信息,见(2)式:
故有

(5)
由极值二阶导数小于零的条件,有λ+R>0。
结合等式(3)和(5),得到
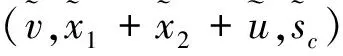
(6)
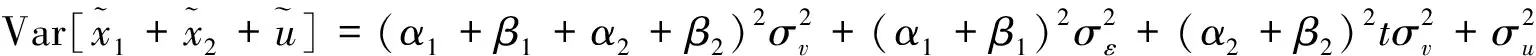
结合等式(3)和(6),得到
而且λ和R必须满足由以上等式确定的约束条件:
(7)
或者等价于最优化问题
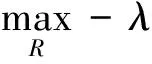
λ和R满足条件(7)。
于是下面利用拉格朗日乘数方法,构造函数
对η求导有
对R求导有
4λ(1+t)(3λ+2R)-2(1+m)t2
则有
从而,α1、α2、β1、β2和γ易得。定理得证。
性质1 当市场处于Bayesian-Nash均衡时,理性内部交易者、启发性内部交易者期望利润和噪声交易者的期望损失分别为
证明由定理1可知,理性内部交易者的期望利润
启发性内部交易者的期望利润
噪声交易者的期望损失

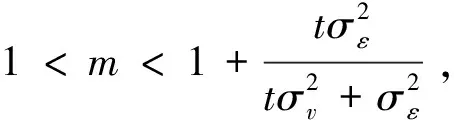
可知,启发性内部交易者的利润大于理性内部交易者。
性质3
1)当t→0时,有
2)当t→∞时,有

2)当t→∞时,有

发现,当公共信息精度t-1→∞时(或等价于t→0)时,启发性内部交易者利润、理性内部交易者利润和噪声交易者损失都为0;当t-1→0时(或等价于t→∞)时,该模型对应于Liu等[10]的模型。
性质4

证明由性质1和性质3有,
可知,与Liu等[10]的模型结果相比,这里公共信息的存在,使得理性内部交易者利润更小,噪声交易者的损失也更小,市场深度更大,监管力度更小。
性质5


2)对t求导知,
可得,若启发性参数m越大,理性内部交易者的利润越小,启发性内部交易者的利润越大,而噪声交易者期望利润不变;当公共信息精度t-1越小,理性内部交易者利润越大,噪声交易者损失越大。
性质5
证明
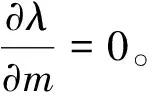
2)分别对t求导,注意到参数m>1,得
可见,若启发性参数m越大,则市场监管力度R越强,而市场深度λ-1不变;当公共信息精度t-1越小,市场深度λ-1越小,而市场监管力度R也越强。
4 结论
本模型建立了一种在市场监管下,理性内部交易者、启发性内部交易者和做市商收到公共信息的内部交易模型。结果表明,当市场处于线性Bayesian-Nash均衡时,启发性内部交易者的利润比理性内部交易者多;公共信息精度t-1越小,导致在监管条件下的理性内部交易者利润越大,噪声交易者损失更大,市场深度越小,监管力度越强;如果启发性内部交易者的重视参数m越大,那么理性内部交易者的利润越小,启发性内部交易者的利润越大,而噪声交易者期望利润不变,市场监管力度越强。

