基于VWAP的价格冲击成本估计及其影响因素研究

燕汝贞，李 平，曾 勇



基于VWAP的价格冲击成本估计及其影响因素研究

燕汝贞，李 平，曾 勇

（电子科技大学经济与管理学院，四川成都，611731）

以交易量加权平均价格（VWAP）为基准估计了证券市场的价格冲击成本，并借鉴Kyle的思想给出了VWAP作为基准价格的理论依据。利用深圳证券市场创业板的高频交易数据，分析了订单规模、价差、成交价格、订单不平衡量等市场微观结构指标对价格冲击的影响。研究发现，对于中盘股和小盘股而言，订单规模与价格冲击具有显著的正相关关系，而大盘股股票订单规模对价格冲击的这种影响并不显著；无论是大盘股、中盘股还是小盘股，价差和订单不平衡量对价格冲击都具有显著的正影响，而成交价格与价格冲击存在负相关关系。据此，本文认为，为了减少价格冲击成本，投资者所制定的交易策略应将大额订单拆分为多个中小规模的子订单，并选择市场流动性较好的时期（开盘后较短时间内）逐次提交。

算法交易；隐性交易成本；价格冲击；交易量加权平均价格

0 引言

传统投资理论假设，金融市场具有完美的流动性，投资者所提交的任何订单均可无成本地被执行，因而投资者只需关注在不同市场环境下如何构建最优投资组合。然而，在现实证券市场上，受市场流动性有限等因素的影响，投资者所提交的订单在执行过程中可能会产生较大的价格冲击成本[1]。为了降低价格冲击成本，投资者通常利用算法交易将大额订单拆分为多个中小规模的订单，并择机逐次提交到证券市场[2-5]。

为了估计价格冲击成本，早在1985年，Kyle在理性预期框架下推导出市场可预期交易量对证券价格变化的影响是一种线性关系，并利用交易量与价格变化的回归系数来刻画价格冲击程度[6]。根据这种估计方法，Glosten和Harris[7]、Ryu[8]、Cont等[9]、Bowe等[10]学者分析了交易方向、市场流动性、公司规模、订单不平衡量等因素对股票市场价格冲击的影响。然而，对于特定的投资而言，当需要执行某种交易策略时，不但需要估计Kyle提出的可预期的市场交易量对证券价格变化的影响程度，更需要考虑自己的订单对市场造成的额外冲击成本。事实上，从交易策略角度来看，真正的价格冲击是指投资者的订单被执行后所引起证券价格的变化[11,12]。对于一个买单而言，价格冲击成本的大小等于订单的执行价格与市场上不存在此订单时的证券价格的差额。

在现实市场上，由于这两个价格不可能同时存在，因此在计算价格冲击成本时，许多学者提出利用某一基准价格来刻画市场上订单不存在时的证券价格，如昨日收盘价[13]、交易日的证券最高价和最低价的平均值[14]、交易日的证券最高价、最低价、开盘价、收盘价的平均值[15]等。然而，这种采用一个或几个特殊时刻的证券价格作为基准价格，并不能反映在整个交易时期内证券的所有交易信息。为了解决这一问题，Berkowitz和Logue[16]提出了一个新的基准价格——交易量加权平均价格（Volume Weighted Average Price，VWAP），并利用订单的执行价格与VWAP基准价格的差额来度量价格冲击。所谓的VWAP基准价格是以每一时期交易量占总交易量比值为权重，对整个交易时期内成交价格进行加权平均。需要指出的是，虽然许多学者在计算价格冲击时常采用VWAP基准价格，但现有文献并没有给出这一基准价格合理性的理论依据。为此，本文借鉴Kyle[6]的思想，从市场微观结构理论的角度指出，VWAP实际上是市场可预期交易量对证券价格进行冲击后形成的期望值。因此，对特定的投资者而言，VWAP可视为市场上不存在自己提交订单时的基准价格。在此基础上，投资者可以准确地估计当执行特定订单时需要额外承担的价格冲击成本。

利用深圳证券交易所创业板2011-2012年的高频交易数据，本文估计了投资者的价格冲击成本，并分析了投资者的订单规模、买卖价差、成交价格以及订单不平衡量等因素对价格冲击的影响及其在日内不同交易时段的差异。研究结论表明，相对于大盘股，即便是相同规模的订单，投资者在交易小盘股时会承担更大的价格冲击成本。无论是大盘股、中盘股还是小盘股，买卖价差和订单不平衡量对价格冲击都具有显著的正影响，成交价格与价格冲击存在负相关关系。对于中盘股和小盘股而言，订单规模对价格冲击具有显著的正影响，而对大盘股股票此影响并不显著；与其他时期相比，在开盘后的第一个交易时期内，订单规模因素对价格冲击的影响最小。

本文的创新性主要体现在：一方面，给出了VWAP基准价格合理性的理论依据，并据此估计了价格冲击成本；另一方面，利用深圳证券市场创业板的高频交易数据，从信息和流动性角度分析了影响价格冲击的主要因素，并对比分析这种影响在不同交易时段之间的差异，相关研究结论可为投资者制定合理交易策略提供重要的参考依据。

本文以下内容的结构为：第一部分给出了VWAP基准的理论依据和价格冲击的估计方法；第二部分实证分析了影响价格冲击的因素；最后一部分为研究结论。

1 VWAP基准价格的理论依据与价格冲击的度量

在整个交易时期内，证券的总交易量和价格变化量之间存在如下关系：

将（1）式除以（2）得：

（3）

在订单全部执行后，证券的预期价格为：

本文利用VWAP基准价格计算价格冲击成本，即价格冲击成本等于订单执行价格与VWAP基准价格的差额。由于不同证券的价格可能存在较大差异，所以借鉴Hu[17]、Chiyachantana等[18]的方法对价格冲击进行标准化，即：

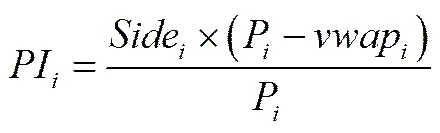
2 实证研究设计

2.1 研究假设

在证券市场上，投资者所提交的订单规模越小，则订单越容易被快速地执行，其价格冲击成本也较小。反之，如果投资者的订单规模较大，且要求在较短时间内全部执行，则会产生较大的价格冲击成本。进一步，与中盘股和小盘股证券相比，大盘股证券的流通市值和成交量均较大，投资者的订单可能会隐藏在众多其他投资者订单中进行交易，导致其订单对价格冲击的影响不明显。基于此，本文提出如下假设。

假设一：对于中盘股和小盘股而言，订单规模与冲击成本存在一个正相关关系，而对大盘股证券这种关系可能并不成立。

在流动性较好的市场上，投资者的订单可快速、低成本的被执行。如果市场缺乏足够流动性，投资者在交易过程中会承担较大的价格冲击成本。Lillo等[19]指出流动性是影响证券市场价格冲击的一个重要因素。如果证券市场具有足够的流动性，那么投资者可以迅速、低成本的执行交易；否则，投资者可能承受较大的交易成本，且交易速度较慢，甚至可能出现交易难以完成的情形。本文利用市场微观结构研究中常用的相对买卖价差来衡量证券市场的流动性，并提出如下假设：

假设二：价差与价格冲击成本正相关，即价差越小，价格冲击成本也越小。

除此之外，Foster和Viswanathan[20]利用NYSE交易数据发现，日内流动性呈现出“U”型特征。进一步，屈文洲和吴世农[21]利用深圳证券市场数据研究发现，我国证券市场流动性也呈现出“L”型模式，即在开盘后的一段较短时间内流动性较好，随后流动性逐渐变差，直至收盘。因此，本文提出如下假设：

假设三：与日内其他时段相比，在开盘后的较短时间内证券的价格冲击较小。

2.2 样本数据

证券的流通市值越大，价格冲击越小，而对于价格冲击特别小的证券，其研究意义不大。因此，本文主要针对流通市值较小的证券，研究价格冲击的主要影响因素。本文选取深圳市国泰安信息技术有限公司提供的创业板高频交易数据，时间跨度为2011年1月4日至2012年12月30日。按照证券的流通市值的大小，分别选取大盘股、中盘股和小盘股证券各1组，每组20只证券，共60只证券。同时，删除明显存在记录错误的数据，如买卖报价为零，最低卖价小于最高买价等。

2.3 相关变量

本文所研究的被解释变量是价格冲击成本，主要的解释变量是订单规模和买卖价差。为了控制市场可预期交易量和价格水平对价格冲击成本的影响，解释变量还包括订单不平衡量和成交价格等变量。由于无法获得投资者的账户交易数据，本文利用市场预期外交易量来刻画投资者总的订单规模（），即每笔交易量与过去5天的平均交易量的差额。同时，还利用此平均交易量指标对每笔订单的规模进行了标准化处理。

在影响价格冲击的因素中，流动性是一个重要的指标。本文利用市场微观结构研究中常用的相对买卖价差来衡量证券市场的流动性。在交易时期内，证券市场的平均相对买卖价差为：

对特定的投资者而言，其他投资者的交易意愿可通过观察限价指令簿的变化情况来推测。为了控制这种由其他投资者的交易行为对价格冲击的影响，本文采用订单不平衡程度来代表市场可预期交易量。借鉴雷觉铭等[22]和陈收等[23]计算订单不平衡量的方法，即订单不平衡量等于卖方报价深度和买方报价深度的差额，在交易时期内，市场不平衡量为：

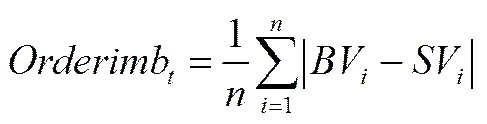
市场深度也是反映证券市场流动性的重要指标之一，其主要是衡量市场在某一特定价位上市场能够实现的交易量。在这一价位上能够成交的证券数量越大，市场深度越大，市场的流动性越好。市场深度也可以利用订单成交金额进行计算，本文采用金额深度方式计算市场深度，其计算公式为：

3 实证结果与分析

3.1 描述统计分析

将整个日内交易时间看作一个交易时段，表1描述了大盘股、中盘股和小盘股中各变量的描述性统计结果。从表1中可以看出，平均而言，大盘股股票的冲击成本最小，小盘股股票的冲击成本最大。相对而言，小盘股0.03%的价格冲击成本略小于Berkowitz[8]的价格冲击水平。此外，相对于中盘股和小盘股，大盘股股票相对价差更小，说明证券的流通市值越大，相对价差越小，流动性越好，其价格冲击也越小。

表1 描述性统计

注：价格冲击，交易量，相对买卖价差，成交价格，订单不平衡量。价格冲击、相对买卖价差、订单规模的单位是百分比；订单不平衡量的单位是股；成交价格和深度的单位是元。

3.2 回归分析

以价格冲击成本为被解释变量，订单规模和买卖价差为主要解释变量，成交价格和订单不平衡量等为控制变量的多元回归模型为：

从表2可知，对中、小盘股而言，订单规模是影响价格冲击的显著因素，并且订单规模越大，向市场上所传递的信息更多，对证券价格的冲击也越大。受大盘股证券流通市值和成交量较大的影响，投资者的订单可能会隐藏在众多其他投资者订单中进行交易，从而使其价格冲击不明显。因此，假设一成立。

作为衡量市场流动性的重要指标，价差也是价格冲击的显著影响因素。无论是大盘股、中盘股还是小盘股，相对价差越小，市场流动性越好，价格冲击也越小，即假设二成立。需要特别说明的是，与现有研究结论一致，我们发现无论是大盘股、中盘股还是小盘股，代表市场可预期交易量的订单不平衡程度与价格冲击均存在显著的正相关关系。此外，成交价格与价格冲击存在显著的负相关关系，即成交价格越大，价格冲击成本越小。

表2 回归结果

注：括号内的数值是估计系数对应的值。***表示在1%的置信水平下显著；**表示在5%的置信水平下显著；*表示在10%的置信水平下显著。下同。

为了进一步考察投资者的订单提交时机问题，本文还将整个日内交易时间分为8个相等的交易时段（30分钟作为一个交易时段），利用小盘股数据，分析在不同交易时段订单规模、相对买卖价差、成交价格、订单不平衡量对价格冲击的影响。采用面板数据分析中的截面固定效应模型进行回归估计，结果如表3所示。

从表3可以看出，在日内8个不同的交易时段中，相对价差、订单不平衡量对价格冲击具有显著的正向影响，成交价格对价格冲击具有显著的负向影响。除第1个交易时段外，订单规模在其他交易时段对价格冲击的影响都是显著的。换言之，如果投资者选择在开盘后的第1个时段提交订单，即便是规模较大的订单，其订单中的私人信息也可以较好地隐藏于其他投资者的大量订单中而不会产生较大的价格冲击。相对于日内其他交易时期，开盘后第1个时段内价差对价格冲击的影响更小。因此，假设三成立。

表3 不同交易时段的回归结果

表3 不同交易时段的回归结果

12345678 0.0930.423***0.186***0.120***0.260***0.174***0.277***0.227*** (0.299)(0.000)(0.000)(0.001)(0.000)(0.000)(0.000)(0.003) 0.188***0.265***0.256***0.223***0.265***0.233***0.217***0.252*** (0.000)(0.000)(0.000)(0.000)(0.000)(0.000)(0.000)(0.000) 0.356***0.211***0.248***0.202***0.235***0.227***0.229***0.142*** (0.000)(0.000)(0.000)(0.000)(0.000)(0.000)(0.000)(0.000) 0.006***0.003**0.003***0.003***0.002**0.0020.003***0.004*** (0.000)(0.019)(0.004)(0.003)(0.032)(0.111)(0.005)(0.000) AdjR20.210.100.160.130.180.150.120.14

3.3 稳健性检验

利用深度衡量市场流行性指标时，市场深度也是影响价格冲击的显著因素，且深度越大，市场流动性越好，证券的价格冲击越小。相关结果如下所示：

利用市场深度指标来衡量市场的流动性，建立如下回归模型：

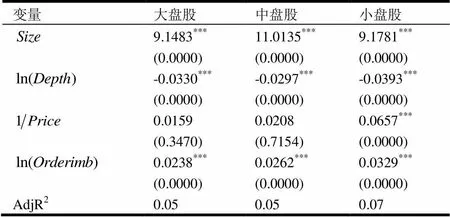
表4 回归结果

比较表2和表4的结果可知，本文得到的回归结果是稳健的，并且代表市场流动性的变量系数的估计值是显著的，说明流动性是影响证券价格冲击的一个显著因素，且市场流动性越好，证券的价格冲击越小。

4 实证结果与分析

本文利用常用的VWAP基准价格计算投资者在执行交易过程中的价格冲击成本，并借鉴Kyle[6]（1985）的思想从理论上证明了VWAP基准价格的合理性。进一步，采用深圳证券交易所创业板的高频交易数据，实证检验了投资者的订单规模、买卖价差、订单不平衡程度、成交价格等市场微观结构变量对价格冲击的影响，并对比分析了这种影响在日内不同交易时段之间的差异。

研究结果表明，无论是大盘股、中盘股还是小盘股证券，相对价差、订单不平衡量对价格冲击都具有显著的正向关系，成交价格对价格冲击具有显著的负向关系。对中盘股和小盘股证券而言，订单规模是影响价格冲击成本的显著因素，即订单规模越小，价格冲击也越小。由于大盘股证券的流动市值和成交量较大，所以大盘股证券订单规模对价格冲击的影响并不显著。因此，为了减少价格冲击成本，提高投资收益，投资者所制定的交易策略应将大额订单拆分为多个中小规模的订单，并在开盘后较短时期内逐次提交。

[1] Wagner W H, Edwards M. Best execution [J]. Financial Analysts Journal, 1993, 49: 65-71.

[2] Florackis C, Gregoriou A, Kostakis A. Trading frequency and asset pricing on the London Stock Exchange: Evidence from a new price impact ratio [J]. Journal of Banking & Finance, 2011, 35: 3335-3350.

[3] Kissell R, Malamut R. Algorithmic decision-making framework [J]. The Journal of Trading, 2006, 1(1): 12-21.

[4] 卞世博,刘海龙. 市场风险与违约风险同时存在下的最优资产配置[J]. 管理工程学报, 2013, 27(1): 160-165.

[5] 燕汝贞, 李平, 曾勇. 基于市场冲击成本与机会成本的算法交易策略 [J]. 管理学报, 2012, 9(7): 952-959.

[6] Kyle A S. Continuous auctions and insider trading [J]. Econometrica, 1985, 53(6): 1315-1335.

[7] Glosten L R, Harris L E. Estimating the components of the bid/ask spread [J]. Journal of financial Economics, 1988, 21(1): 123-142.

[8] Ryu D. Price impact asymmetry of futures trades: Trade direction and trade size [J]. Emerging Markets Review, 2013, 14: 110-130.

[9] Cont R, Kukanov A, Stoikov S. The price impact of order book events [J]. Journal of Financial Econometrics, 2013, 12(1): 47-88.

[10] Bowe M, Hyde S, Mcfarlane L. Duration, trading volume and the price impact of trades in an emerging futures market [J]. Emerging Markets Review, 2013, 17: 89-105.

[11] Eisler Z, Bouchaud J-P, Kockelkoren J. The price impact of order book events: market orders, limit orders and cancellations [J]. Quantitative Finance, 2012, 12(9): 1395-1419.

[12] Kissell R, Glantz M. Optimal trading strategies: Quantitative approaches for managing market impact and trading risk [M]. New York: AMACOM, 2003.

[13] Keim D B, Madhavan A. Transactions costs and investment style: An inter-exchange analysis of institutional equity trades [J]. Journal of Financial Economics, 1997, 46(3): 265-292.

[14] Blum G A, Kracaw W A, Lewellen W G. Determinants of the execution costs of common stock trades by individual investors [J]. Journal of Financial Research, 1986, 9(4): 291-301.

[15] Domowitz I, Glen J, Madhavan A. Liquidity, volatility and equity trading costs across countries and over time [J]. International Finance, 2001, 4(2): 221-255.

[16] Berkowitz A S, Logue E D. The total cost of transactions on the NYSE [J]. Journal of Finance, 1988, 43(1): 97-112.

[17] Hu G. Measures of implicit trading costs and buy-sell asymmetry [J]. Journal of Financial Markets, 2009, 12(3): 418-437.

[18] Chiyachantana C N, Jain P K, Jiang C, et al. International evidence on institutional trading behavior and price impact [J]. The Journal of Finance, 2004, 59(2): 869-898.

[19] Lillo F, Farmer J D, Mantegna R N. Master curve for price-impact function [J]. Nature, 2003, 421(9): 129-130.

[20] Foster F D, Viswanathan S. Variations in trading volume, return volatility, and trading costs: Evidence on recent price formation models [J]. The Journal of Finance, 1993, 48(1): 187-211.

[21] 屈文洲, 吴世农. 中国股票市场微观结构的特征分析——买卖报价价差模式及影响因素的实证研究 [J]. 经济研究, 2002, (1): 56-63.

[22] 雷觉铭, 李平, 曾勇. 深圳股市价差影响因素的实证研究 [J]. 管理学报, 2010, 7(10): 1535-1541.

[23] 陈收, 李双飞, 黎传国. 订单差、交易量变化对股票价格的冲击 [J]. 管理科学学报, 2010, 13(9): 68-75.

Estimation of Price Impact Cost Based on VWAP and it’s Factors

YAN Ru-zhen, LI Ping, ZENG Yong

(School of Management and Economics, University of Electronic Science and Technology of China, Chengdu 611731, China)

The investor’s order can be executed in the financial market with perfect liquidity based on traditional investment theory. Investors are mainly concerned with the inability of their investment portfolio to achieve a target return. However, the execution process is very important in the competitive securities market. If investors expect to reach a target return, they must have a suitable portfolio and low transaction cost. If the cost is larger than return, the return of investment will not reach the target, even if an optimal portfolio exists. Transaction costs refer to costs incurred after making an investment decision. The transaction cost components consist of taxes, commissions, price appreciation, price impact, timing risk, and opportunity cost. Price impact accounts for the largest percentage of total transaction cost. Hence, it is very important to understand what key factors influence the price impact for the investors.This paper estimates the price impact cost based on the volume weight average price (VWAP), and finds a theoretical foundation of VWAP from the model proposed by Kyle (1985). Furthermore, this paper uses the data of growth enterprises market in China to estimate the price impact of investors, and analyzes the factors influencing price impact cost, including order size, spread, stock price and order imbalance. Meanwhile, this paper also describes the difference of those factors in different periods. The results show that the price impact of the small-cap share order is higher than the large-cap share for investors, even if the orders have the same size. Order size is positively associated with the price impact for middle-cap and small-cap shares, but not large-cap share. With the decreasing order size, the price impact of the orders is gradually decreasing. The order size is insignificantly positively associated with the price impact influenced by the large market value and trading volume in large-cap stocks. In addition, order imbalance and spread are significantly positively related to the price impact for large-cap, middle-cap, and small-cap shares, while the stock price is significantly negatively related to the price impact. The direct implication of this study is that the investor should break a block order into small orders and submit the small orders to the market in the period of higher market liquidity. Meanwhile, this study also provides an important basis for choosing the optimal trading strategy.

algorithmic trading; implicit trading cost; price impact; volume weight average price

中文编辑：杜 健；英文编辑：Charlie C. Chen

F830.9

A

1004-6062(2016)03-0129-05

10.13587/j.cnki.jieem.2016.03.016

2013-11-04

2016-04-18

国家自然科学资助基金（71171034、71301019）；中央高校基本科研业务费专项资金

燕汝贞（1982—），男，山东淄博人；博士生，研究方向：算法交易，证券市场微观结构。