基于受限位移约束的蚁群算法在航班着陆调度问题中的应用研究

马卫民，杨文娟，徐 博



基于受限位移约束的蚁群算法在航班着陆调度问题中的应用研究

马卫民1,2，杨文娟1，徐 博2

(1.西安工业大学经济管理学院，陕西西安710021；2.同济大学经济与管理学院，上海 200092)

航班着陆调度问题是机场跑道调度中的重要问题，合理的调度策略将极大的减少航班延误。本文提出基于受限位移约束的蚁群算法(CPS-AC)，该算法利用了蚁群算法高效的全局搜索能力，同时结合CPS确保调度的可操作性和公平性，能够为实际的空中交通流量管理提供理论方法和依据。数值模拟实验结果表明，CPS-AC算法明显优于经典的先到先服务(FCFS)的调度方法和标准的蚁群算法(AC)，能在较短时间内有效减少着陆航班的总延迟时间，且具有较好的收敛性。这些对于减少航班延误，提高着陆容量具有推动作用。

受限位移约束(CPS) ; 蚁群算法；航班着陆调度

0 引言

近年来，随着我国民航产业的迅速发展，空域拥堵问题也越来越严重，由此引起的航班延误问题不仅给航空公司造成巨大的经济损失，而且严重威胁到机场及空域的安全。合理调度到达航班对于保障飞行安全、降低延误损失以及提高顾客满意度等具有重大意义。

传统的对到达航班流的调度方式通常采用先到先服务(FCFS)策略。它基于管制员的工作经验，在满足各种限制条件下按照先到先下降的策略为到达航班制定着陆次序和着陆时间，使队列中航班的总延误时间最小。在交通繁忙时，FCFS策略往往导致跑道利用效率低下，空中滞留航班过多而危及飞行安全。为解决这些问题，国内外学者提出了许多优化方法[1-5]。

比较突出的两种方法是受限位移约束(CPS)和蚁群算法。Dear等人首次提出受限位移约束的思想[6]，即在调度时，相对于飞机初始在FCFS中的位置，只允许其向前或者向后移动个位置(为最大受限位移)。这一做法可以大大缩小搜索空间，同时使可操作性更强。随后大量的学者在CPS的框架下设计新的算法[7-12]。其中，最新的研究成果是Balakrishnan和 Chandran用动态规划方法求出了航班着陆调度问题的最优解[13]。但该求解算法仅适用于的取值较小的情形。蚁群算法是首先由意大利学者Dorigo[14]提出的一种新型的启发式搜索方法。它具有分布式、正反馈机制和贪婪式搜索的优点，具有很强的全局搜索能力，首先应用于TSP问题，并取得较好的结果。此后，该算法被普遍应用于各种领域，如单机调度问题、车辆调度等。Randall第一次将蚁群算法应用于跑道调度问题[15]。随后Bencheikh等多次利用蚁群算法去生成最初的解来处理单跑道和多跑道的调度问题[16,17]。Zhan 等结合滚动时域控制原理(Receding Horizon Control)对机场实时跑道调度问题进行了研究[18]。在国内，胡祥培等[19]对蚁群算法的相关领域进行了评述。此外，许多学者也将蚁群算法应用到航班着陆调度问题中[20-22]。

本文结合上述的受限位移约束和蚁群算法，提出基于受限位移约束的蚁群算法(CPS-AC)来解决航班着陆调度问题。这样一方面利用蚁群算法强大的全局搜索能力，另一方面结合CPS确保了调度的可操作性和公平性，能够较好的应用于实际的交通管理系统中。更重要的是，蚁群算法结合CPS进行研究，可以弥补以往对CPS研究的不足。这是因为，用经典的动态规划方法求解CPS模型，只能解决当飞机的最大受限位移较小时的情形。随着求解问题的规模的增大(飞机允许前后移动的最大位置变大)，动态规划方法求解的算法复杂度将呈指数增加[13]，从而不能得到一个较好的解。而CPS-AC算法能够在这种情况下给出一个不错的可行解，从而拓展了经典CPS模型的求解适用范围。

1 航班着陆调度问题模型和CPS策略

1.1航班着陆调度模型

航班着陆调度问题是为了尽可能的减少航班延误，即对于一些给定的需要下降的航班，怎样使它们在空中的总延迟时间最小。对于需要下降的架航班，假设调度后的航班着陆序列为，令为序列中的第架航班(位于位置),则航班着陆调度问题需要优化的目标函数为

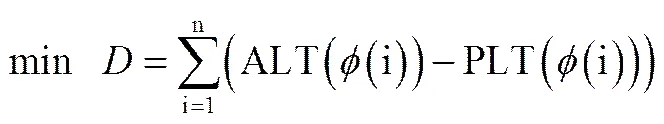
(2)

1.2CPS策略

CPS策略是指某架飞机在调度后的位置与其初始在FCFS中的位置之差要控制在一定范围内，即某飞机在调度过程中，相对于初始位置，其最多向前或者向后移动个位置。如有架航班，航班在FCFS队列中的位置为，则调度后其位置必须在和之间，其中为受限偏移半径，表示调度后位置的偏移量的最大值。表1给出了=6，=1时各个航班的可能位置。

表1=6，=1时航班的可分配位置[13]

1.3 最小时间间隔(MST)

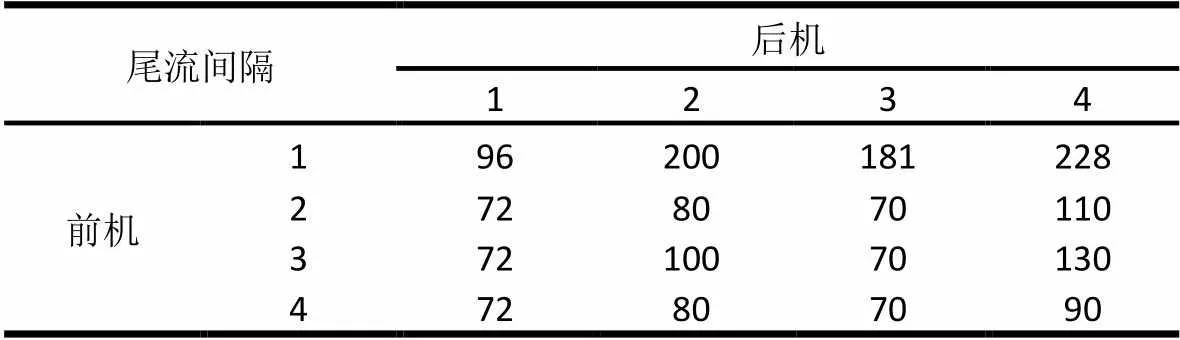
为飞机制定最小时间间隔是为了避免飞机产生的尾涡流对后机的影响，对于不同类型的航班，其产生和抵抗尾涡流的能力也不相同，因此要根据飞机类型及着陆次序制定不同的最小时间间隔(MST)。如表2所示，一架波音727在一架波音 747 之后降落需要的MST为200s，而一架波音747在一架波音 727之后降落需要的MST仅为72s。

表2 飞机尾涡流间隔标准(s)[23]

尾流间隔后机 1234 前机196200181228 2728070110 37210070130 472807090

注：1=Boeing 747, 2=Boeing 727, 3=Boeing 707, 4=DC9

2 基于CPS的蚁群算法设计

本文结合CPS与蚁群算法的优势，提出CPS-AC算法。这主要是为弥补当最大受限位移较大时经典动态规划算法无法求解CPS的不足，同时确保了调度的公平性，使该算法能够更好的运用于现实的交通管理系统中。CPS-AC算法的设计思路如下：

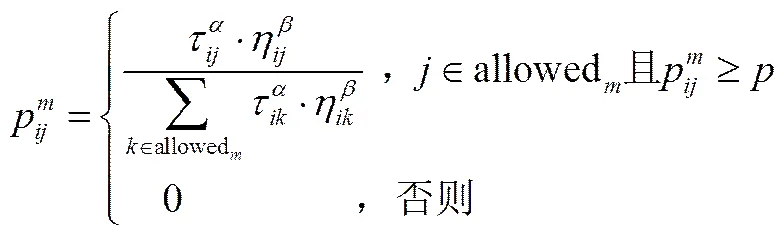
(4)

(2)信息素更新策略

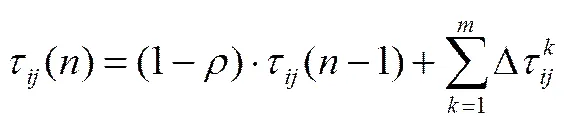
(6)

3 航班着陆调度的CPS-AC算法描述

CPS-AC算法结合CPS策略改进了经典的蚁群算法，一方面提高了运行速度，另一方面给出的调度策略更加贴近实际。下面给出CPS-AC算法求解航班着陆调度问题的具体步骤：

Step2: 结合在CPS约束中每个位置可能的航班分配和状态转移概率公式选择下一个位置的待着陆航班。

Step3: 检查每只蚂蚁的禁忌表，即为一个航班排序组合，并按公式(2)计算该组合中每架航班的着陆时间，从而得出每只蚂蚁所选择序列的总延迟时间。找出本次循环中最小的总延迟时间，记为，对应的飞机排序组合为。若，则，否则不变。

Step4：按公式(5)和公式(6)更新信息素。

4 数值试验与仿真

为检验CPS-AC算法的模型求解的可行性和求解效果，本文在最大受限位移取值较小()和较大时(=5,10),分别将CPS-AC算法与FCFS算法和传统的蚁群算法(AC)进行比较,并对算法的稳定性进行了分析(如图1)。其中CPS-AC算法选取的参数分别为：=1；=5；=0.1；=100；=150；=100。

在MATLAB2013a环境下实现了CPS-AC算法与AC算法。

此外，为进一步检查该测试结果的稳定性，更好的对AC-CPS和AC以及FCFS进行比较，分别对于表3中的数据进行50次仿真计算，得出的结果如表4所示。可见，大量的数值统计结果仍然证实了上述结论的正确性。

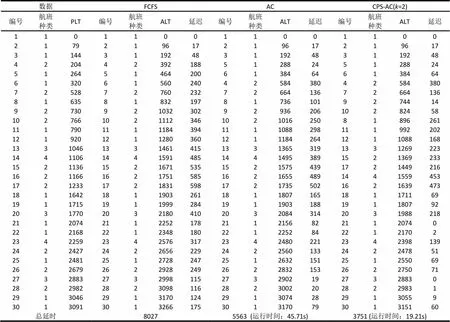
表3 FCFS、AC算法、CPS-AC算法得到的航班排序结果

由表5可以看出，标准的蚁群算法(AC)在航班数量较少时()能取得一定的优化结果(延误时间比FCFS调度方法减少了10%～14%)，当航班数量较多时(),AC算法很难进行优化，且运行时间较长。对于CPS-AC算法，当=5时，CPS-AC算法得到的航班着陆队列的总延迟时间比FCFS调度方法减少了26%～38%；当=10时，CPS-AC算法得到的航班着陆队列的总延迟时间减少了17%～36%。随着航班数量和最大受限位移增大(求解问题规模变大)，算法的效率会有一定程度的降低。但是，这个趋势是可控的，即使在求解问题规模较大()时，该算法仍能较为有效的减少航班延误。

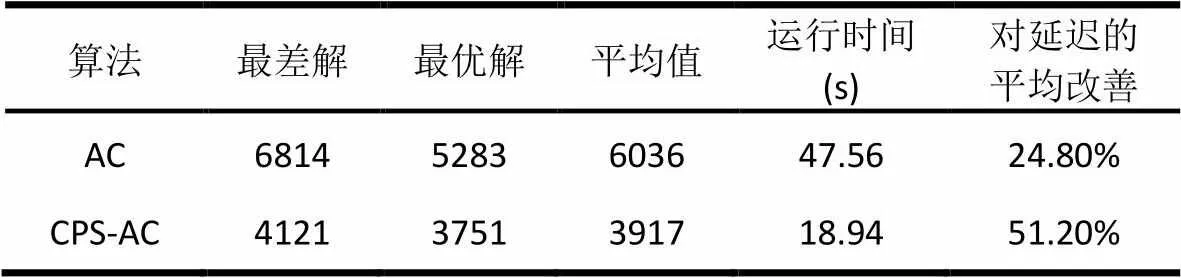
表4 AC算法、CPS-AC算法的比较

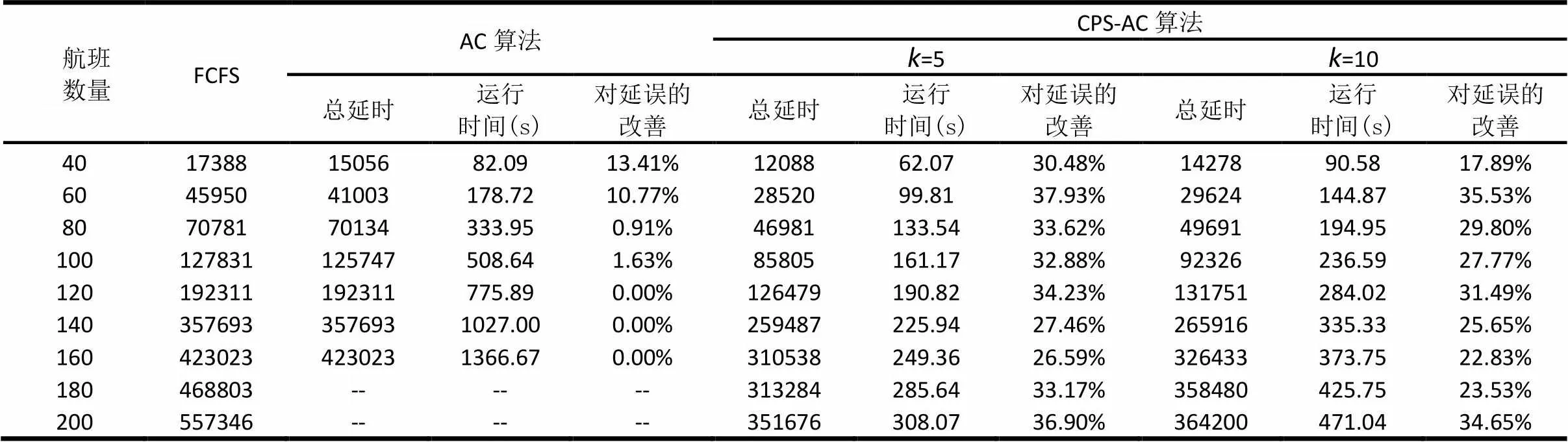
表5 FCFS、AC算法、CPS-AC算法的总延迟时间的比较（k=5,10）

(3)算法的稳定性

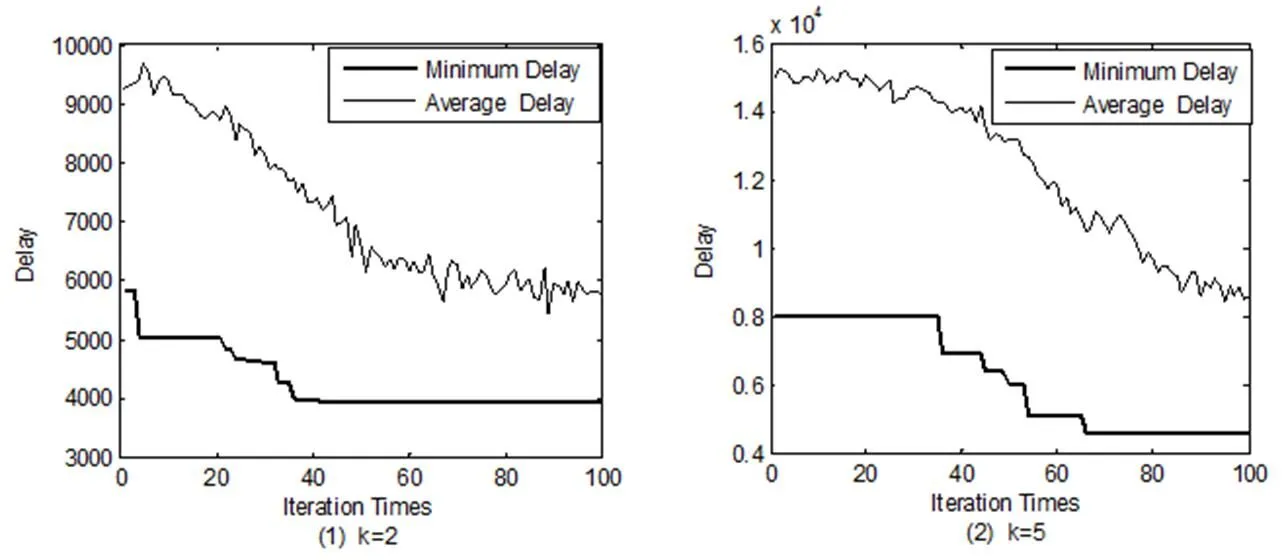
图1CPS-AC算法的收敛性

5 结论

本文为解决航班着陆调度问题，提出了一种新的解决框架，即将CPS与蚁群算法相结合。这样既利用蚁群算法强大的全局搜索能力和较好的收敛性，又加入CPS约束，避免了由于着陆队列次序的调整幅度较大而引起的某些航班过于靠后的情况，在一定程度上体现了航班降落的公平性，同时也减小了管制人员的工作负荷。更为重要的是，CPS-AC算法拓展了经典CPS模型的求解适用范围，给出CPS中当最大受限位移较大情况下的可行解。文章最后通过仿真将CPS-AC算法与FCFS调度方法和标准蚁群算法(AC)分别进行比较，结果表明，该算法明显优于FCFS调度方法和标准的蚁群算法，在值较大及航班数量较多的情况仍能有效减少着陆航班的总延误时间，从而在一定程度上降低航班延误成本并减少航空公司的经济损失。此外，在算法中更有效的设置约束条件以满足现实复杂空管约束，以及将该算法扩展到多跑道航班着陆调度问题中是我们今后进一步的研究方向。

[1] Briskorn D, Stolletz R. Aircraft landing problems with aircraft classes[J]. Journal of Scheduling, 2014, 17: 31-45.

[2] Tavakkoli-Moghaddam R, Yaghoubi-Panah M, Radmehr F. Scheduling the sequence of aircraft landings for a single runway using a fuzzy programming approach[J]. Journal of Air Transport Management, 2012, 25: 15-18.

[3] Beasley JE, Krishnamoorthy M, Sharaiha YM, et al. Scheduling aircraft landings-the static case[J]. Transportation Science, 2000, 34(2): 180-197.

[4] 余江，蒲云. 飞机着陆调度优化——带移动时间窗的隐枚举算法[J]. 系统工程理论方法应用，2004, 13(2): 182-186.

[5] 应圣钢，孙富春, 胡来红，等. 基于多目标动态规划的多跑道进港排序[J]. 控制理论与应用，2010, 27(7): 828-835.

[6] Dear RG. The dynamic scheduling of aircraft in the near terminal area[R]. MIT Flight Transportation Report R76-9, Massachusetts Institute of Technology, Cambridge, 1976.

[7] Psaraftis HN. A dynamic programming approach for sequencing groups of identical jobs[J]. Operations Research, 1980, 28(6): 1347-1359.

[8] Dear RG, Sherif YS. An algorithm for computer assisted sequencing and scheduling of terminal area operations[J]. Transportation Research, Part A, Policy Practice 1991, 25(2-3): 129-139.

[9] Neuman F, Erzberger H. Analysis of delay reducing and fuel saving sequencing and spacing algorithms for arrival spacing[R]. NASA technical report A-91203; NAS 1.15:103880; NASA-TM-103880. Retrieved August 2008, NASA Technical Reports Server (NTRS), 1991.

[10] Trivizas DA. Optimal scheduling with maximum position shift (MPS)constraints: A runway scheduling application[J]. Journal of Navigation 1998, 51(2): 250-266.

[11] de Neufville R, Odoni AR. Airport Systems: Planning, Design and Management[J]. McGraw-Hill, New York, 2003.

[12] Carr FR. Robust decision-support tools for airport surface traffic[D]. Ph.D. thesis, Massachusetts Institute of Technology, Cambridge, MA, 2004.

[13] Balakrishnan H, Chandran BG. Algorithms for scheduling runway operations under constrained position shifting[J]. Operations Research, 2010,58(6):1650-1665.

[14] Dorigo M, Gambardella LM. Ant colony system: A cooperative learning approach to the traveling salesman problem [J]. IEEE Transactions on Evolutionary Computation, 1997, 1(1): 53-56.

[15] Randall MC. Scheduling aircraft landings using ant colony optimisation[C]. In: Proceedings of The IASTED international conference artificial intelligence and soft computing, Banff, Canada, 2002.

[16] Bencheikh G, Boukachour J, Alaoui AEH, et al. Hybrid method for aircraft landing scheduling based on a job shop formulation[J]. Int J Comput Sci Netw Secur 2009, 9: 78-88.

[17] Bencheikh G, Boukachour J, Elhilali Alaoui A. Improved Ant Colony Algorithm to Solve the Aircraft Landing Problem[J]. International Journal of Computer Theory and Engineering 2011, 3(2): 224-233.

[18] Zhan ZH, Zhang J, Liu O, et al. An efficient ant colony system based on receding horizon control for the aircraft arrival sequencing and scheduling problem [J]. IEEE Transactions on Intelligent Transportation Systems, 2010, 11(2): 399-412.

[19] 胡祥培，丁秋雷，李永先. 蚁群算法研究评述[J]. 管理工程学报，2008,22(2): 74-79.

[20] 张涛, 胡佳研, 李福娟, 等. 基于ASRank和MMAS的蚁群算法求解飞机指派问题[J]. 管理工程学报，2012,26(2): 148-155.

[21] 陈欣, 杨文东, 陆讯, 等. 一种终端区飞机排序问题的蚁群算法研究[J]. 山东大学学报(工学版)，2007, 37(6): 111-117.

[22] 李志荣, 张兆宁. 基于蚁群算法的航班着陆排序[J]. 交通运输工程与信息学报，2006, 4(6): 66-69.

[23] Bianco L, Dell’Olmo P, Giordani S. “Scheduling models and algorithms for TMA traffic management,” in Modelling and Simulation in Air Traffic Management[J]. New York: Springer-Verlag, 1997: 139-167.

[24] Willemain TR, Fan H, Ma H. Statistical analysis of intervals between projected airport arrivals[R]. DSES Technical Report 38-04-510, Rensselaer Polytechnic Institute, Troy, NY, 2004.

Ant Colony Algorithm Based on Constraint Position Shifting for Aircraft Landing Problem

MA Wei-min1,2, YANG Wen-juan1, XU Bo2

(1.School of Economics and Management, Xi’an Technological University, Xi’an 710021, China;2.School of Economics and Management, Tongji University, Shanghai 200092, China)

Aircraft landing scheduling problems are salient in the airport runway system. A reasonable scheduling method can greatly reduce the total delay time of aircrafts. Thus, an increasing number of scholars focus on developing various optimization methods to tackle these problems. Two prominent approaches are Constraint Position Shifting (CPS) and Ant Colony (AC) algorithm.

CPS stipulates that all aircrafts are only allowed to move at mostpositions forward or backward from their FCFS (First-Come-First-Served) order, whereis the maximum position shift. It reduces the search space for large scale problems and maintains some level of fairness among different airlines. AC algorithm, another widely used method, is a highly efficient heuristic algorithm, which is firstly developed by Dorigo in travelling salesman problems (TSP). It has many important advantages, such as positive feedback mechanism, greedy search mode and strong global searching ability.

By combining the advantages of AC and CPS mentioned above, we propose the resultant CPS-AC strategy. This new strategy is effective to tackle aircraft landing scheduling problems. It has strong global-search ability and ensures the maneuverability of scheduling and fairness among airlines. At the same time, it reduces controllers’ workload to a certain extent. More importantly, in the course of solving CPS model, a reasonable solution can be obtained when the value ofis not small. This is an important achievement since the classical Dynamic Programming, which is widely used to solve CPS model, only presents effective solutions whenis typically small. AC is an important supplement of problem-solving technology for CPS when k is large.

To test the efficiency of the CPS-AC algorithm, we present some experimental tests where FCFS strategy (First Come First Served) and traditional ant colony algorithm (AC) are used to compare with CPS-AC. First, we test a case whereis set to be 2 and the number of aircrafts () is 30. The results show that CPS-AC algorithm reduces 53.27% of the total delay time more than FCFS strategy, whereas AC reduces 30.70% of the total delay time. The runtime of CPS-AC algorithm is also smaller than that of AC algorithm. That is to say, CPS-AC algorithm is more efficient in reducing the total delay time whenis small. To verify the performance of CPS-AC algorithm when the scale of problem is large, we conduct a series of tests whereis set from 40 to 200 andis set to be 5 and 10, respectively. Similarly, the results also reveal that CPS-AC algorithm is still very promising. CPS-AC algorithm not only outperforms FCFS but also AC algorithm. At last, we analyze the convergence of the CPS-AC algorithm, which has a good convergence.

The paper is concluded with a summary of our research findings, implications and future research directions.

constrained position shifting (CPS); ant colony algorithm; aircraft landing scheduling

中文编辑：杜 健；英文编辑：Charlie C. Chen

V351.11

A

1004-6062(2016)01-0191-06

10.13587/j.cnki.jieem.2016.01.024

2014-04-26

2014-10-31

国家自然科学基金(71071113, 71161016)；全国优秀博士论文作者专项资金资助项目(200782)；高等学校博士学科点专项科研基金(20100072110011)；上海市哲学社会科学规划课题(2010BZH003)

马卫民(1971—), 男，陕西合阳人。西安工业大学经济与管理学院、陕西省百人计划特聘教授，同济大学经济与管理学院教授(博导)，研究方向：运筹与运作管理、优化理论与方法。