低碳环境下供应链纵向减排合作的动态协调策略
赵道致,原白云,徐春秋
低碳环境下供应链纵向减排合作的动态协调策略
赵道致,原白云,徐春秋
(天津大学管理与经济学部,天津 300072)
低碳环境下,考虑供应链上下游企业减排合作效果的跨期性和低碳产品需求的特征,借助微分博弈研究了单个供应商和单个制造商长期合作的两级供应链中合作减排问题。假设需求是产品减排量的线性函数,分别分析了供应链减排中制造商占主导供应商跟随的Stackelberg博弈情形及制造商与供应商纵向合作减排的情形,构建了两种情形下的动态模型,得到了各自相应的反馈均衡策略及产品碳排放量随时间变化的最优轨迹;并比较这两种反馈均衡策略,发现合作减排策略能提高产品的减排量,供应商和制造商以及整个供应链系统的利润也比非合作减排时有所提高,实现了供应链企业间的协调;最后,通过数值分析,验证了结论的有效性,并对相关参数进行了灵敏度分析,为供应链企业间的合作减排提供理论依据。
低碳;供应链;合作减排;微分博弈;Stackelberg博弈
0 引言
近年来,各国政府、企业和学者已经形成共识,温室效应是导致全球气候变化以及极端气候频繁出现的主要原因,而人类在经济活动中产生的碳排放是导致温室效应的主要根源[1]。在低碳背景下,各国政府及企业都在积极探讨减少温室气体排放的解决方案,全球已有12个国家和地区立法,要求其企业实行碳标签制度,1000多家著名企业将“低碳”作为其供应链的必需,沃尔玛、IBM、宜家等均已要求其供应商提供碳标签。2013年3月国家发展改革委发布了《低碳产品认证管理暂行办法》,明确了我国低碳产品的认证体系的主要内容[1]。低碳产品认证可以发动消费端推动节能减排。通过低碳产品认证,企业的产品被贴上低碳产品的认证标志,消费者将能够放心选择购买,从而推动企业进行减排技术创新,努力开发低碳产品。低碳产品认证体系也对很多产业的产业链上下游产生很大的影响,企业在生产产品过程中会对其上下游的企业提出相应的减排要求,因此低碳环境下从运营管理角度探讨供应链上下游企业间合作减排问题具有重要的现实意义。
1 相关文献的回顾
目前已有学者从生产运营的角度研究了企业的减排决策行为,杜少甫等[2]研究了确定需求下,考虑企业依赖碳排放权交易机制且有多种排放权获取渠道时,企业的生产优化模型。Zhang等[3]在随机需求下也做了相关的研究,借助报童模型建立了企业依赖碳排放权交易机制下的生产库存优化决策模型。Hua 等[4]借助EOQ模型,研究了确定性需求下,仅考虑存在碳排放权交易机制时,企业的最优订货批量问题。Song & Leng[5]借助报童模型,进一步研究了随机需求下,分别考虑了三种碳排放限制政策(强制减排、征收碳税和碳总量限制和交易)时,企业单周期最优订货量的决策问题。Zhang & Xu[6]研究了碳总量限制和交易机制下,考虑多产品独立随机需求下,企业的多类产品生产计划制订的问题,但这类文献均没有在供应链框架下考虑上下游企业联合减排的问题。
随着全球市场竞争的日渐加剧,供应链管理受到了越来越多企业的高度重视。一些文献研究了供应链网络设计对其供应链碳排放的影响,Elhedhli & Merrick[7]将碳排放量约束引入到供应链网络设计中,构建了整体成本最小化模型,借助拉格朗日松弛算法得到满足碳排放约束且成本最小的供应链整体方案,通过合理设计供应链网络中的车辆调度以降低供应链整体的碳排放量。Benjaafar等[8]在不同的碳排放限制政策(碳税、碳中和碳总量限制和交易)下,通过建立成本最小化模型,探究了同一个供应链内的企业间联合减排对他们运营成本和碳排放的影响,并且提出了一些激励供应链上下游企业寻求合作减排的策略。Jaber等[9]研究了两阶段供应链中制造商和零售商联合减排的问题,通过最优化制造商的产品生产率及制造商和零售商之间的协调因子,实现双方库存成本和减排成本的最小化。但这类文献没从博弈的角度,考虑供应链上下游企业间的合作减排问题。
陈剑[10]在对当前供应链管理研究现状综述的基础上,指出低碳时代供应链管理值得重点关注的几个重要方向,其中包括引入碳交易市场的供应链运作优化以及低碳供应链上不同利益主体间运作的协调与优化等。Du 等[11]在考虑存在碳排放权交易情况下,在由非营利绿色环保组织作为碳排放权的供应商和依赖碳排放权的企业组成的新型供应链中,基于报童模型研究了依赖排放权的供应链双方的Stackelberg博弈过程。Du等[12]进一步考察了这种依赖碳排放权的供应链,将政府制定碳排放限额作为可变参数,引入了公平偏好和社会总福利,通过分析该供应链双方的Stackelberg博弈过程,研究了政府制定的碳排放限制政策对排放权供应商和排放权需求商运营的影响。但这类文献没考虑减排对产品需求的影响,也没有涉及动态架构下供应链上下游合作减排的问题。
实践中企业的减排行为会影响产品的市场需求,部分环保意识较强的消费者,具有一定程度的低碳偏好,更愿意购买低碳产品。Laroche等[13]的研究表明,随着消费者环保意识的增强,越来越多的消费者愿意为环保产品支付更高的价格;Plambeck[14]通过实证研究也证实,公司自愿披露产品相关的环境信息,诸如碳排放量等信息,能增加产品的市场份额和消费者的信任。Liu等[15]指出生产和销售环保产品的主要受益来自于消费者环保意识引起的需求的增加,环保型厂商应该采取一些营销手段,引导消费者增加环保意识,激励非环保消费者转变成环保消费者。
另外,实践中企业的减排投资行为往往存在一定的滞后效应,当前的减排努力会影响到以后企业的碳排放,而且企业的减排投资也是个持续的过程,如果某个时期终止减排行为,未来企业的碳排放可能会出现反弹增加,发改委发布的《低碳产品认证管理暂行办法》[3]也指出低碳产品认证证书的有效期为3年,这说明企业的减排行为是个长期的动态过程,减排投资的效果存在跨期效应,在动态架构下研究供应链上下游企业间合作减排问题更加贴近现实,文献[16]曾用动态模型描述了环境污染的优化控制问题,但该文献未从低碳角度考虑减排对需求的影响。
不同与以往文献,本文在低碳环境下,考虑产品需求受产品减排量的影响,从动态的角度研究了由单个供应商和单个占主导的制造商组成的两级供应链中纵向减排合作问题。文中借助微分博弈模型,首先分析了非合作模式(Stackelberg博弈情形)下,占主导的制造商和跟随的供应商各自的减排决策过程;随后分析了合作模式下双方的减排决策过程,并对两种情形进行比较,试图寻求一种最优的供应链纵向减排合作机制,以实现供应链整体绩效的提升。
2 问题描述与假设
2.1 问题描述
图1供应链上下游企业联合减排行为机理示意图
2.2 符号说明
2.3 基本假设
该问题相关的4个假设条件如下:
1)假设企业的减排成本是关于减排努力程度的凸函数,文中减排成本函数借鉴文献[16]对广告成本函数的假设,时刻制造商和供应商的减排成本分别为:
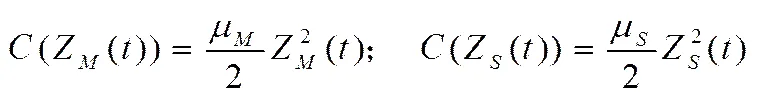
2)产品的减排量是一个动态变化的过程,产品的减排量受当期制造商和供应商的减排努力程度及当期产品的减排量影响,可用式(2)所示的状态方程(微分方程)表示产品减排量的变化过程:
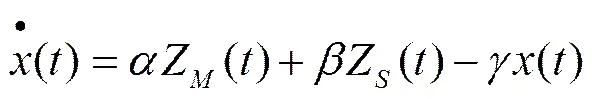
3)产品的需求受产品减排量的影响,借鉴文献[15]中关于消费者环保意识影响产品需求的函数形式,文中假设时刻需求与产品减排量呈线性关系,表示如下:
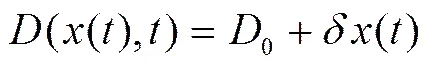
4)另外,本文主要考虑减排对供应链上下游企业的影响,因此不考虑供应链双方的库存成本和缺货成本,不考虑价格等其他因素对需求的影响。假设双方决策基于完全信息,供应链参与方均是理性决策者。
3 模型构建及求解
本节主要研究以下两种情形:1)非合作减排情况下制造商主导的Stackelberg博弈情形,假设制造商作为供应链上核心企业,在产品减排决策中充当领导者角色,而供应商作为减排控制的跟随者,制造商对其的减排投资予以支持,为其支付一定比例的减排成本。2)合作减排情况下,制造商和供应商都意识到减排对企业利润的影响,双方积极进行减排纵向合作,以供应链系统总利润最优集中进行减排决策,并对利润增加部分进行合理分配。
3.1 非合作微分博弈(制造商主导的Stackelberg博弈)情形
在无限时间长度之内,供应链系统中的两个成员(制造商和供应商)任意时刻均具有相同的贴现因子,记为;双方的目标都是在无限时区内寻求使其利润最大化的最优减排策略。制造商和供应商的目标函数分别为:
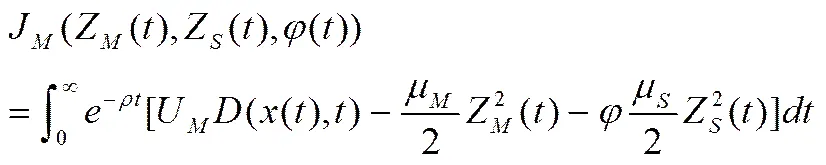
(5)
其中,制造商和供应商寻求最优减排策略的过程构成了双人微分博弈。制造商和供应商的最优减排行动由反馈策略决定。由于动态参数条件下求解解析解的困难,文中借鉴文献[16]的处理,假设模型中所有参数和都是与时间无关的常数,且博弈在无限时区的任何时段内,参与人面对的是相同的博弈,因此可将策略限制在静态策略,即制造商和供应商的减排策略分别表示为和,其均衡为静态反馈均衡(为简化书写,下文不再列出时间)。
命题1:制造商主导的Stackelberg博弈情形下,制造商和供应商关于减排努力程度的静态反馈Stackelberg均衡策略分别为:,产品减排量的最优轨迹为:;且双方各自的利润最优值函数为:,;
证明:为得到此博弈的反馈Stackelberg均衡策略,运用逆向归纳法,首先作为跟随方的供应商视制造商的减排努力程度和成本分担比例为给定参数,以此决策自身的最优减排努力程度,这便转化成了供应商的单方最优化控制问题。由(5)式知,记时刻之后供应商的总利润现值最优值函数为:
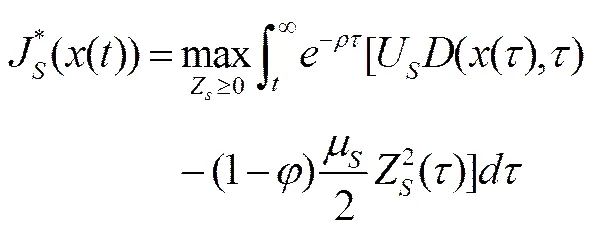
(7)
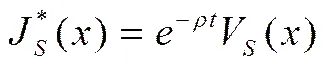
(9)
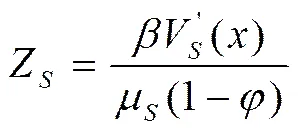
(11)
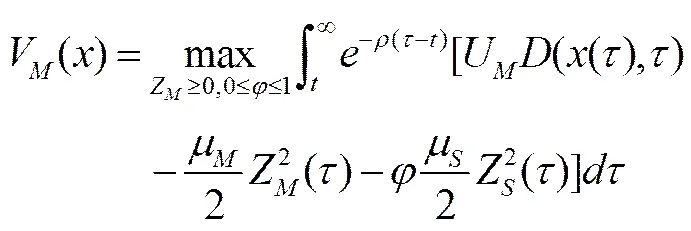
(13)
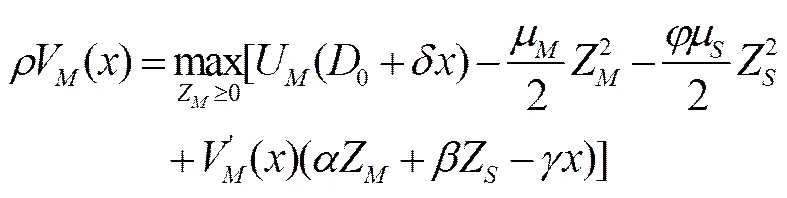
将(10)式代入(14)式,整理可得:
(15)
同理,由一阶条件可解得:
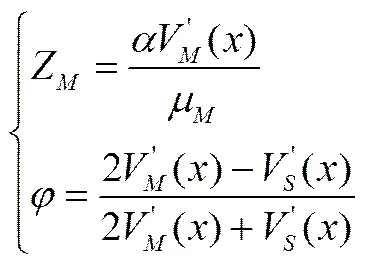
将(10)式和(16)式分别代入(9)式和(14)式,整理可得:
(17)
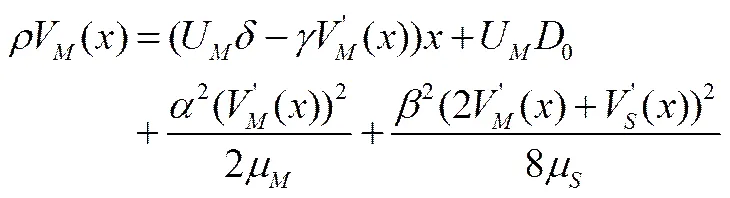
注意到微分方程(17)式和(18)式的阶数特点,推测关于的线性函数是HJB方程的解。令:
(19)
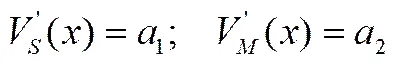
将(19)式和(20)式分别代入(17)式和(18)式,得到:
(21)
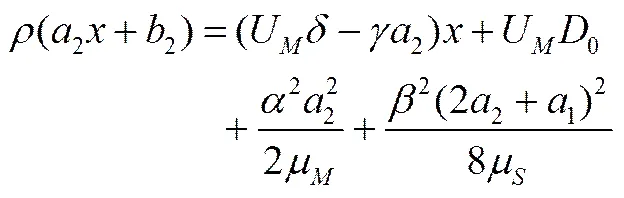
对比(21)式和(22)式左右两边的同类项系数,可得关于、和、系数的方程组如(23)式所示:
(23)
求解方程组(23)式,可得:
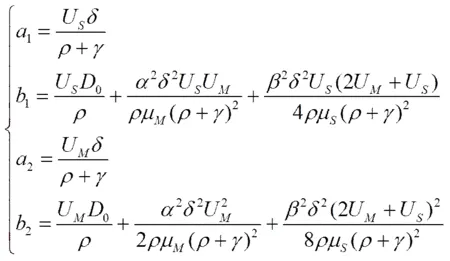
将(24)式代入(20)式,可得:
(25)
将(25)式分别代入(16)式和(10)式,可得制造商和供应商的静态反馈Stackelberg均衡策略为:
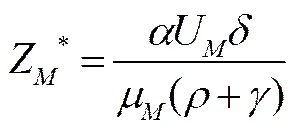
(27)
(28)
将(24)式代入(19)式,可得供应商和制造商利润当值最优值函数为:
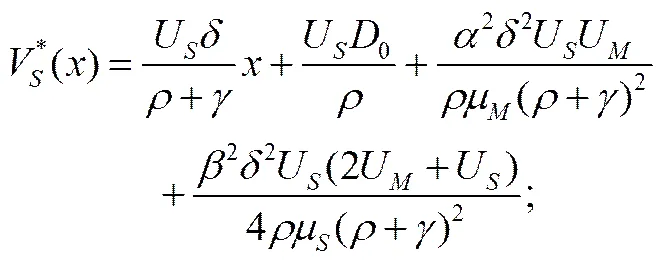
(30)
将(29)式和(30)式分别代入(8)式和(13)式,即可得制造商和供应商的利润最优值函数,;
此时将(26)式和(27)式代入状态方程式(2)中,可解得产品减排量的轨迹为:
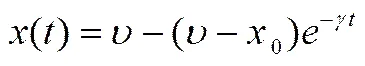
3.2 制造商和供应商减排合作的博弈情形
在制造商和供应商进行减排合作博弈情形下,双方以供应链系统利润最优为首要原则共同地来确定和的值。此时供应链系统的目标函数为:
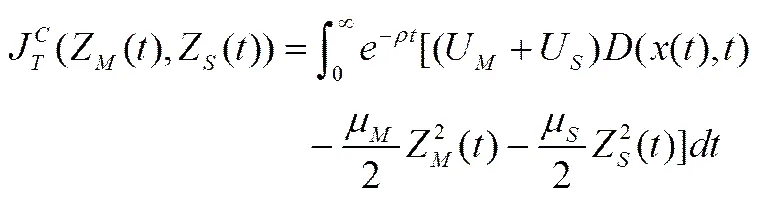
命题2:制造商和供应商减排合作博弈情形下,制造商和供应商关于减排努力程度的静态反馈均衡策略分别为:,产品减排量的最优轨迹为:
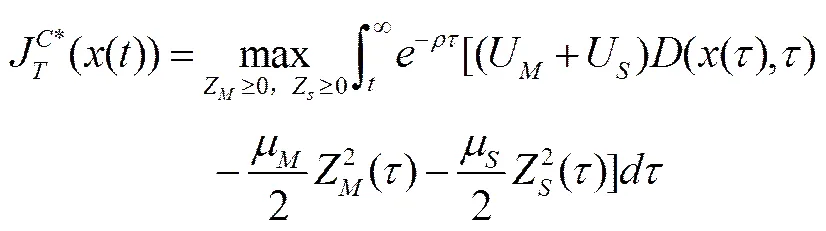
(34)
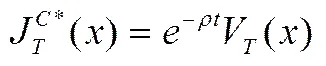
(36)
由一阶条件可解得减排合作情形下制造商和供应商的最优减排策略:
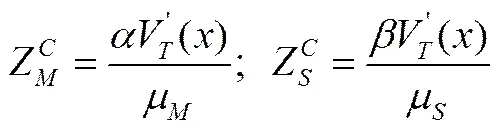
将(37)式代入到(36)式可得:
(38)
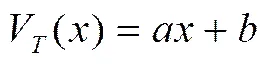
(40)
将(40)式代入(37)式,可得减排合作博弈情形下制造商和供应商关于减排努力程度的静态反馈均衡策略为:

将(40)式代入(39)式,可得合作情形下供应链系统总利润当值的最优值函数:
(42)
将(42)式代入(35)式,即可得供应链系统的利润最优值函数。
此时将(41)式代入状态方程式(2)中,可解得产品减排量的轨迹为:
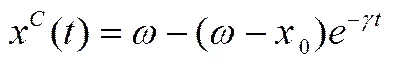
另外,观察命题1和命题2提供的制造商和供应商的反馈均衡策略,均与时间无关,这也反映了该策略在企业减排实践中的操作性较强,作为连续时间范围内供应链系统,最优策略不需要随时间每时每刻都在变化,给企业的实践操作带来了可行性,一定程度上体现了该模型的管理实践意义,由命题2的推导还可以得到如下推论:
推论1:制造商和供应商减排合作博弈情形下,制造商和供应商的最优减排努力程度、以及供应链系统的利润均与双方产品的边际利润和、产品减排量对产品需求的影响系数以及各自减排努力程度对产品减排量的影响系数和呈正比关系;与各自的减排成本系数和及产品减排量的自然衰减率呈反比关系。
证明略(观察(41)式和(42)式,容易证得推论1)。
推论1说明,当消费者低碳意识较强(即产品减排量对产品需求的影响系数较大)时,供应链上下游企业愿意进行更多的减排投入,以增加供应链双方的利润;当供应链双方的减排努力容易转化为产品减排量的增加(即减排努力程度对产品减排量的影响系数或较大)时,供应链参与方也有加大减排投资的热情;而当减排投资成本系数(或)较大时,或者减排投资设备容易老化(产品减排量的自然衰减率较大)时,会一定程度阻碍企业减排投资的积极性,这种情况下,政府可以采用行政干预,考虑提供技术补贴激励企业进行减排投资,以减少其对环境的污染,这也将是我们未来要研究的问题之一。
3.3 两种情形的比较
本小节试图对Stackelberg主从博弈和合作博弈这两种情形下制造商与供应商的最优减排努力程度以及供应链系统的最优总利润进行比较,由此得到命题3。
命题3:减排合作博弈情形下,制造商和供应商的最优减排努力程度均高于Stackelberg博弈情形下的对应值,即,;供应链系统的总利润也高于Stackelberg博弈情形下的对应值,即,实现了供应链系统的Pareto最优。
证明:对比命题1和命题2,由(26)式、(27)式和(41)式可得:
(44)
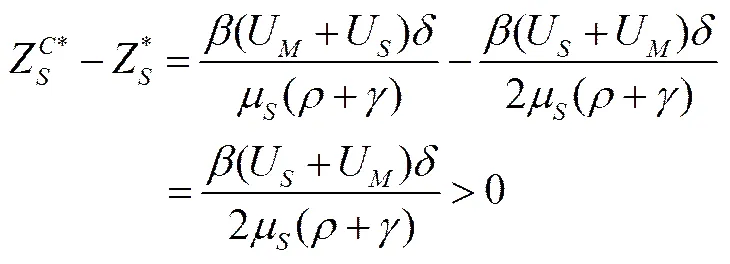
由(42)式、(29)式和(30)式可得:
(46)
至此命题3得证。
命题3说明,与非合作减排相比,制造商和供应商的合作减排能够促使双方投入更多的减排努力,并能实现供应链系统整体利润的提升,低碳环境下这意味着供应链上下游企业在进行纵向合作减排动态决策时,不仅考虑了供应链系统长期利润的最大化,还遵循了“经济—社会—环境”三重底线(Triple Bottom Line)的原则[18],考虑了企业需承担的社会责任及长期生产对环境造成的影响。
在以往研究供应链上下游协调的静态模型[13]中,也有得到过类似命题3的结论:与非合作博弈情形(Stackelberg主从博弈)相比,合作博弈情形下,制造商和供应商各自的利润及供应链系统的总利润均有所增加。因此命题3恰好从动态角度验证了低碳环境下,在供应链上下游企业间长期开展减排合作同样能够使双方长期总利润增加,实现共赢,这为供应链上下游企业如何进行长期减排决策以及如何确定最佳的合作减排水平等方面提供了理论依据。
值得注意的是,制造商和供应商的合作减排虽然能够实现供应链整体利润的最大化,但要使双方自愿参与合作减排,还必须满足参与约束,即制造商和供应商参与合作减排后各自分得的利润比非合作时各自的利润要大。因此制造商和供应商进行合作减排时,最优减排努力策略必须满足下列参与约束:
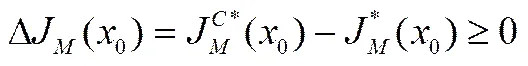
(48)
4 算例分析
本节将对制造商和供应商的Stackelberg博弈和合作减排博弈分别进行算例分析,以验证模型的有效性,并在合作减排情形下进行相关参数的灵敏度分析,给定相关参数值如下:
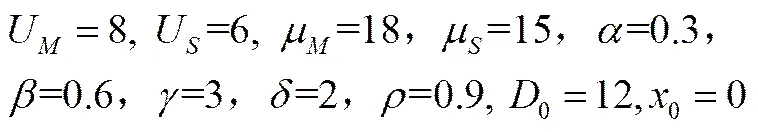
将给定参数值分别代入命题1和命题2,可解得:
1)Stackelberg博弈情形下制造商和供应商的最优减排努力程度及供应链系统的最优利润:;;;
2)合作减排情形下制造商和供应商的最优减排努力程度及供应链系统的最优利润:;;;
3)Stackelberg博弈情形下和合作减排情形下产品减排量的最优轨迹为:;;
上述算例验证了命题3的结论,合作减排模式下,制造商和供应商的最优减排努力程度高于Stackelberg博弈情形下的对应值;供应链系统的总利润也比Stackelberg博弈情形下的总利润高,表明供应链长期纵向合作减排能够促进供应链双方的减排投入,给双方带来更多的利润。
两种情形下产品减排量的最优轨迹曲线如图2所示:
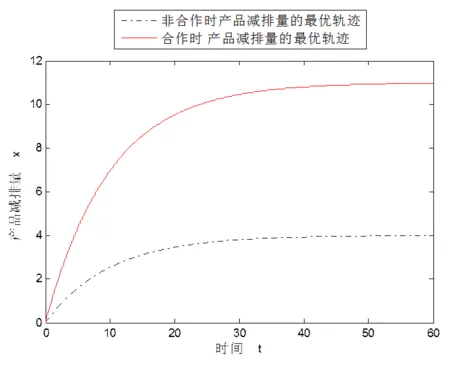
图2两种情形下产品减排量的最优轨迹
由图2可以看出,产品的减排量随时间变化逐渐增加并趋于稳定,表明该供应链系统的减排过程是可控的,且同一时刻供应链纵向合作减排情形下产品的减排量始终高于非合作情形下的值,这表明这种纵向合作减排模式不仅实现了供应链系统利润的最大化,还兼顾了环境因素,使供应链企业的碳排放量也实现了较大的下降。
下面对相关参数进行灵敏度分析,由于篇幅有限,本文仅分析产品减排量最优轨迹受产品减排量对产品需求的影响系数、制造商减排努力程度对产品减排量的影响系数、制造商的减排成本系数及产品减排量的自然衰减率这四个参数影响的敏感性。其他参数(如:供应商减排努力程度对产品减排量的影响系数、供应商的减排成本系数)的灵敏度分析类似。图3分别描述了不同组参数下产品减排量的最优轨迹曲线。
从图3(a)和(b)中可以看出,随着产品减排量对产品需求的影响系数及制造商减排努力程度对产品减排量的影响系数的增加,产品减排量最优轨迹在同一时刻点的斜率逐渐增加,这表明当消费者低碳意识的增强,越来越消费者愿意购买碳排放量较低的产品,也就是说当产品的市场需求对产品减排量越敏感(即越大)时,供应链长期纵向合作减排的效果越明显(产品减排量最优轨迹在同一时点的斜率越大);同样地,当制造商的减排努力程度较容易转化成产品减排量的下降时,也就是说当产品减排量对制造商的减排努力程度越敏感(即越大)时,供应链长期纵向合作减排的效果越明显(产品减排量最优轨迹在同一时点的斜率越大)。
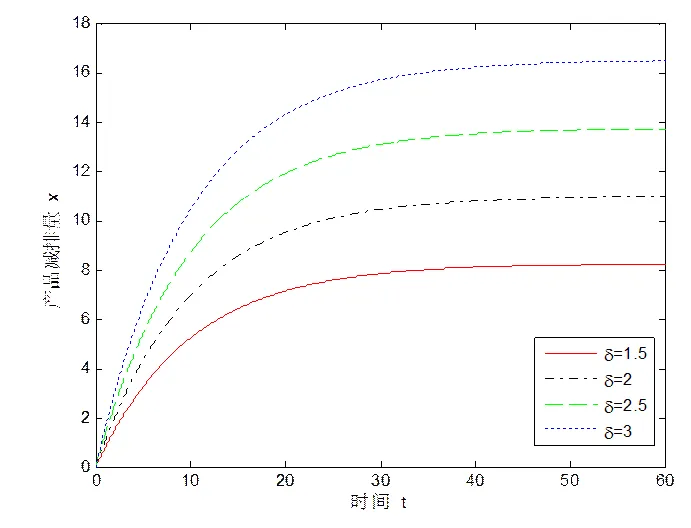
(a)对产品减排量最优轨迹的影响
(b)对产品减排量最优轨迹的影响
(c)对产品减排量最优轨迹的影响
(d)对产品减排量最优轨迹的影响
图3、、及对产品减排量最优轨迹的影响
5 结论与展望
本文在低碳环境下,考虑到减排对需求的影响以及企业减排行为存在跨期效应,引入时间因素,借助微分博弈,探讨了由单个供应商和单个制造商组成的两级供应链中纵向合作减排的动态策略问题。假设需求是产品碳减排量的线性增函数,分别构建了制造商占主导供应商跟随的Stackelberg微分对策模型和制造商与供应商合作减排的动态模型,得到了两种情形下,制造商与供应商各自的最优反馈均衡策略和各自的利润最优值函数,并得到了两种情形下产品减排量随时间变化的最优轨迹;而后对两种情形下的最优反馈策略和供应链整体利润进行比较,发现合作减排情形下,制造商和供应商投入的减排努力程度较高,供应链的整体利润也比非合作时高,实现了Pareto最优;最后,通过数值算例,验证了模型的有效性,并在合作减排情形下,分析了相关参数的灵敏性,为供应链上下游企业长期开展减排合作提供了相关的理论依据。
不足之处是,文中在考虑供应链纵向减排合作的动态策略时,并没考虑到政府政策对企业间减排合作的影响,随着政府对企业碳排放量的限制和碳交易市场的出现,供应链企业间长期纵向减排合作将会出现新的契机和问题;供应链纵向减排合作除了涉及制造商和供应商之间的合作,还涉及到制造商和下游零售商之间减排和低碳推广的合作,因此本论文仅仅是研究供应链企业减排合作动态策略的开端,我们将在后续进行更深入研究。此外,文中为了简化模型,假设制造商和供应商产品的边际利润为常量,而实际中在非合作情形下,供应链节点企业之间的产品交易价格常常是供应链运营的决策变量,因此在现有模型中引入批发价格等决策变量,也是我们未来值得研究的问题之一。
[1] Dinan T. Policy options for reducing CO2 emissions[R]. Washington, D.C., The congress of the United States, Congressional Budget Office, 2008. http://www.cbo.gov/ftpdocs/89xx/doc8934/02-12-Carbon.pdf.
[2] 中国经济导报. 低碳产品认证:期待改变“节能不低碳”怪现象[EB/OL].http://www.ceh.com.cn/ztbd/jnjpzk/146186.shtml, 2012-11-17/2013-3-31.
[3] 国家发展改革委, 国家认监委. 关于印发《低碳产品认证管理暂行办法》的通知[EB/OL]. http://www.sdpc.gov.cn/zcfb/zcfbtz/2013tz/t20130319_533084.htm, 2013-2-18/2013-3-31.
[4] 杜少甫, 董骏峰, 梁樑等. 考虑排放许可与交易的生产优化[J]. 中国管理科学, 2009, 17(3): 81–86.
[5] Zhang J, Nie T, Du S. Optimal emission-dependent production policy with stochastic demand[J]. International Journal of Society Systems Science, 2011, 3(1-2): 21–39.
[6] Hua G, Cheng T C E, Wang S. Managing carbon footprints in inventory management[J]. International Journal of Production Economics. 2011, 132(2): 178–185.
[7] Song J, Leng M. Analysis of the single-period problem under carbon emissions policies[J]. International Series in Operations Research & Management Science, 2012, 176: 297–313.
[8] Zhang B, Xu L. Multi-item production planning with carbon cap and trade mechanism[J]. International Journal of Production Economics, 2013, Published on line, http://dx.doi.org/10.1016/j.ijpe.2013.01.024i.
[9] Elhedhli S, Merrick R. Green supply chain network design to reduce carbon emissions[J]. Transportation Research Part D, 2012, 17(5): 370–379.
[10] Benjaafar S, Li Y, Daskin M. Carbon footprint and the management of supply chains: insights from simple models[J]. IEEE Transactions on Automation Science and Engineering, 2013, 10(1):99–116.
[11] Jaber M Y, Glock C H, Saadany A. Supply chain coordination with emissions reduction incentives[J]. International Journal of Production Research, 2013, 51(1): 69–82.
[12] 陈剑. 低碳供应链管理研究[J]. 系统管理学报, 2012, 21(6): 721–728.
[13] Du S, Ma F, Fu Z, et al. Game-theoretic analysis for an emission-dependent supply chain in a ‘cap-and-trade’ system[J]. Annals of Operations Research, 2011, Published on line, http://dx.doi.org/10.1007/s10479-011-0964-6.
[14] Du S, Zhu L, Liang L, et al. Emission-dependent supply chain and environment-policy-making in the ‘cap-and-trade’ system[J]. Energy Policy, 2012, Published on line, http://dx.doi.org/10.1016/j.enpol.2012.09.042.
[15] Laroche M, Bergeron J, Barbaro-Forleo G. Targeting consumers who are willing to pay more for environmentally-friendly products[J]. Journal of Consumer Marketing, 2001, 18(6): 503–520.
[16] Plambeck E L. Reducing greenhouse gas emissions through operations and supply chain management[J]. Energy Economics, 2012, 34(S1): S64–S74.
[17] Liu Z, Anderson T D, Cruz J M. Consumer environmental awareness and competition in two-stage supply chains[J]. European Journal of Operational Research, 2012, 218(3) 602–613.
[18] Jørgensen S, Martín-Herrán G, Zaccour G. Dynamic games in the economics and management of pollution[J]. Environ Model Assess, 2010, 15(6): 433–467.
[19] Jørgensen S, Sigue S P, Zaccour G. Dynamic cooperative advertising in a channel[J]. Journal o f Retailing, 2000, 76(1):71–92.
[20] Itakura N, Kinbara Y, Fuwa T. Discrimination of forearm’s motions by surface EMG signals using neural network[J]. Application of Human Science, 1996, 15(6):287–294.
[21] A.E. 布赖森, 何硫琦. 应用最优控制—最优化·估计·控制[M]. 北京:国防工业出版社, 1982: 141-143.
[22] Elkington J. Cannibals with Forks: The Triple Bottom Line of 21st Century Business[M]. UK: Capstone Publishing Ltd, 1997: 23–25.
Dynamic Coordination Strategy of Vertical Cooperative on Carbon Emission Reduction in Supply Chain under Low-carbon Era
ZHAO Dao-zhi , YUAN Bai-yun, XU Chun-qiu
(College of Management and Economics,Tianjin University,Tianjin 300072,China)
Research has already shown that global warming has a direct relationship with the emission of carbon and other greenhouse gases. Actions on climate change have been topping priority lists in many countries, especially with increasing pressures from the public. Many countries have attempted to enact legislation or design market-based carbon trading mechanisms for controlling carbon emission. Twelve countries and regions have enacted legislation to require that enterprises carry out carbon labeling systems. More than 1000 famous enterprises require "low carbon" in their supply chains, such as Wal-Mart, IBM, IKEA, which have asked their suppliers to provide carbon labels. On March 2013, The National Development and Reform Commission in China issued provisional rules on the management of low carbon products certification in order to identify the main content of China's low-carbon products certification system. Low-carbon products certification can boost the consumption side to promote energy saving and emission reduction. With low carbon products certification, consumers will be able to purchase products labeled low carbon based on their preferences in order to encourage companies to spend efforts in developing low carbon products. Low-carbon products certification systems have a big impact for upstream and downstream activities in many industries. Firms have focused for the most part on reducing emissions because of physical processes, business practices and operational policies. Thus, it has important practical significance to discuss about emissions reduction through the cooperation between enterprises in upstream and downstream supply chains from the perspective of management.
This study considers that reduction rate can affect the cooperation of carbon emission reduction between enterprises in product demand, and the upstream and downstream supply chains. In addition, this study assumes that demand has a linear relationship with carbon emissions. Vertical cooperation on carbon emission reduction is discussed based on a differential game in a two-stage supply chain consisting of a single supplier and a single manufacturer.
In the first part, we analyzed the Stackelberg game scenario in which manufacturer is a leader and supplier is a follower in the supply chain with the goal of reducing carbon emissions. In addition, we built the Stackelberg differential game models and solved this differential game by using the HJB equation to obtain feedback equilibrium strategy, the optimal function of profit about manufacturer and supplier, and an optimal trajectory for carbon emissions of product.
In the second part, we analyzed the other scenarios in which vertical cooperation between manufacturers and suppliers about emission reduction was presented. Moreover, we attained a feedback equilibrium strategy of manufacturer and supplier and the optimal function of profit about the entire supply chain and optimal trajectory for carbon emissions of product.
After comparing the two feedback equilibrium strategies, this study proposed that vertical cooperation strategies about emission reduction could improve the emissions of product, and the profit of supplier and manufacturer. The entire supply chain system is higher than non-cooperation supply chains because of the coordination among enterprises in the supply chain.
At last, numerical analysis is conducted to verify the validity of conclusions. In addition, sensitivity analysis of the relevant parameters is conducted to understand the cooperation between enterprises in the supply chain.
low-carbon; supply chain; cooperative on carbon emission reduction; differential game; Stackelberggame
中文编辑:杜 健;英文编辑:Charlie C. Chen
C934
A
1004-6062(2016)01-0147-08
10.13587/j.cnki.jieem.2016.01.018
2013-05-01
2013-12-17
国家自然科学基金资助项目(71072155)
赵道致(1956—),男,江苏无锡人,天津大学管理与经济学部教授、博士生导师,研究方向:物流与供应链管理、运营管理、工业工程等。

