无线传感器网络中新的最小暴露路径问题及其求解算法

叶苗，王宇平，代才，王晓丽



无线传感器网络中新的最小暴露路径问题及其求解算法

叶苗1,2,3,4，王宇平1，代才1，王晓丽1

(1. 西安电子科技大学计算机学院，陕西西安 710071；2．桂林理工大学信息科学与工程学院，广西桂林 541004； 3. 桂林电子科技大学广西云安全与云服务工程技术研究中心，广西桂林 541104；4. 陕西师范大学计算机科学学院，陕西西安 710062 )

无线传感器网络中原始的最小暴露路径问题没有考虑对路径的实际限制条件，提出一种要求经过某一特别保护区域部分边界的最小暴露路径问题。由于无法建立相应的图模型，原有求解最小暴露路径问题的经典方法（网格法和维诺图法）对提出的新问题不再起效。先将该问题转化成带约束条件的优化问题，然后针对转化后的数学模型高度非线性、高维度而不好用确定性优化方法的特点，结合问题实际背景设计出混合人工蜂群求解算法。通过在多种情况下的仿真实验发现，设计的带约束条件优化模型和混合人工蜂群求解算法能有效解决提出的最小暴露路径问题。

无线传感器网络；最小暴露路径；保护区域；混合人工蜂群算法

1 引言

无线传感器网络(WSN, wireless sensor networks)由具备感知、数据处理以及无线通信功能的大量传感器节点组成。因为其具有成本低廉和易于扩展的优点，在商业与军事领域内都得到了广泛应用（如环境监控、地震与气象预报、地下与深水探测等）。对WSN的研究与应用也已引起了众多研究者和厂商的高度关注。

覆盖是传感器网络的关键性基础技术之一，它反映了传感器网络对被监测区域的感知能力。覆盖质量的好坏直接影响着监测系统的性能，而它的度量有助于描述出整个网络对被监测目标（静止或运动目标）的覆盖情况，有助于指导传感器节点部署的调整与优化。目前，已经有很多关于其覆盖检测目标能力的度量的讨论[1,2]，基本集中在栅栏覆盖这类问题的讨论上。从被监控对象的特征[1]看，传感器网络中的覆盖问题可以分为区域覆盖、扫描覆盖和栅栏覆盖。栅栏覆盖的研究目的就是找到连接起点与终点的一条或多条路径，使这些路径在不同覆盖质量定义下提供对移动目标感知/监视质量的描述。“暴露穿越[2,3]”同时考虑了“目标暴露”的时间因素和传感器节点对于目标的“感应强度”的空间因素，在数学上可以将其表示为感应强度在时间上沿穿越路径的曲线积分，以此来衡量布置的传感器节点对暴露路径的覆盖质量，这种覆盖模型符合实际环境[2,3]，是栅栏覆盖问题中讨论最早也是最多的一种度量方式。最小暴露穿越对应的路径称之为最小暴露路径，这对应了数学中极值曲线问题[4]（也是数学中泛函极值的变分问题[5]）。数学中求解变分问题的常用方法是求解其对应的欧拉—拉格朗日微分方程[5]，理论上求解这个微分方程就可以求出这条路径的精确表达式。但在多传感器节点场景下对应的欧拉—拉格朗日微分方程高度非线性难于表达更难于求解，因此即使发现了这一问题的数学本质[6~8]，还是没有办法求出其精确解析，文献[6]仅仅是给出了在单个传感器节点情形下的精确解析解。目前只能讨论通常情况下最小暴露路径问题的近似解。目前解决暴露穿越问题中的近似求解方法主要有基于网格划分的路径搜索方法和基于Voronoi图的计算几何方法。Meguerdichian等[9]最早基于网格思想设计出求解暴露穿越问题的方法，该方法先对传感器区域进行正方形网格剖分，再根据节点分布情况计算网格各边的暴露度，最后使用Dijkstra算法等最短路径算法找到一条穿越感知区域且暴露度最小的路径；基于Voronoi图的计算几何方法是由Veltri和Huang等[10]较早提出，通过使用Voronoi图分析移动目标下一候选位置点集合，同时将移动对象在某一时间间隔内沿路径移动的暴露度定义为移动对象沿途所收集到的传感器节点的感应强度。后续出现了对这2种方法的改进和不同场景下的应用：文献[6,7]将维诺图法与单传感器节点情形下的欧拉—拉格朗日微分方程结合提出了一种改进方法，文献[8]将网格法运用在异向传感器节点的最小暴露路径的求解上,这些都属于网格法和维诺图法的变种和一些特定场合下的应用。

但是在实际的传感器网络覆盖问题中，覆盖区域中各个位置的重要性有可能不同，比如中间某些区域更加敏感，同时由于客观条件的限制（如高温或环境恶劣、或是危险敏感区域）无法达到，无法事先在这样区域内布置传感器节点，只能在其周围布置传感器节点来保护这个区域。移动目标从固定的起点出发，到达这个敏感区域后只能沿着这个区域的边界移动，再到达固定的终点。如图1所示的路径中有连续的一小段是这个敏感区域的部分边界，这时需要定量地给出传感器网络对移动目标沿着某条路径达到从起点到终点时的监视能力，并在此前提下找出具有最小暴露度的路径。为方便描述，这样的敏感区域在本文中称为特别保护区域，和文献[2,3]讨论的问题对应，所求的这条路径称为带特别保护区域边界条件约束的最小暴露路径。数学中对应这种问题的原型为拟极值曲线问题[4]也称为泛函极值中的单侧变分问题[4,5]。同前面的介绍一样，无法通过数学上求解欧拉—拉格朗日偏微分方程的办法来求解。又由于有保护区域边界条件的限制，无法建立相应的带权图模型，前面介绍的网格法和基于Voronoi图的计算几何方法这2种基本的近似求解方法也不再适用。为解决这类问题，本文先将带特别保护区域边界条件约束的最小暴露路径问题抽象为一个带约束的多元最小值的优化问题，该最优化问题是一个高维且高度非线性复杂问题，传统的数学优化方法很难找到其全局最优解，在人工蜂群算法的框架下，本文结合问题特点设计出混合人工蜂群求解算法。通过系列的实验证实了所设计的模型和求解算法能很好地求解这种新的最小暴露路径问题。

2 问题描述

2.1 暴露度及最小暴露路径

文献[2,3]首次给出了暴露度的定义。假设在感应区域范围内分布有个传感器用于监测穿越区域范围内的移动目标，这些传感器节点可以通过某些定位机制获取自己的位置信息[11~13]，并且可以通过某些机制[14~16]保证这些节点对周围区域覆盖的可靠性。移动目标从某一固定出发点出发沿着某条路径穿越区域到达某一固定终点，文献[2,3]给出的暴露度的数学定义为

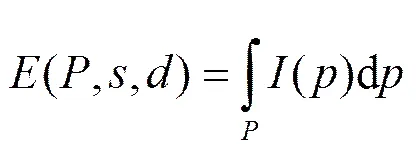
最小暴露路径问题后文又为原始最小暴露路径问题，就是求出在所有连接起点和终点的路径中使暴露度最小的那条路径。假设路径可以表示成函数=()的形式，则关于暴露度的定义式(1)就是函数()的函数，可以用数学中泛函[6~8]描述为

(2)

这时最小暴露路径问题就可以表示为

2.2 带特别保护区域边界条件约束的最小暴露路径问题

在实际应用场合中，感应区域中某个区域是需要重点保护的。但由于客观条件的限制，比如地理空间限制或者环境恶劣、或危险敏感区域无法到达，从而无法在保护区域内布置传感器节点，只能事先在这个区域的周围布置传感器节点来保护这个特别保护区域；移动目标无法进入该区域内，在固定起点接近该区域后只能沿着该区域的边界移动，然后在边界的某点离开后到达固定终点。比如在图1中，曲线(,)=0内的区域是敏感区域，需要重点保护，由于客观条件的限制，区域(,)<0内部无法布置传感器节点，只能在(,)>0的区域外布置传感器节点来保护(,)<0的区域。移动目标从点出发，沿着某路径达到保护区域上的某点，然后沿着边界到达某点，再沿某条路径从达到终点。在所有这样的路径中，找出暴露度值最小的那条路径。这就是带特别保护区域边界条件约束的最小暴露路径问题，对应数学中拟极值曲线问题[4]。

这时带必经区域边界的最小暴露路径问题就可以表示为

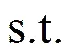
图1 带特别保护区域边界条件约束的最小暴露路径问题

3 带特别保护区域边界条件约束的最小暴露路径问题的多元最优化模型

对原始最小暴露度路径问题[2,3]，常见的求解方法有网格法[9]和维诺图法[10]，这二者方法最终都是将问题抽象成一种图模型进行求解。然而，网格法对本文提出的带必经区域边界条件约束的最小暴露路径问题并不起作用，原因在于约束条件的存在会导致约束区域边界位置对应的网格节点的权值无法计算，从而不能建立对应的带权图模型。维诺图法对于本文提到的带特别保护区域边界条件约束的最小暴露路径问题维诺图法也是无效的，原因也是在于约束条件的存在破坏了保护区域边界与维诺顶点之间连接关系，无法建立对应的带权图模型。在引言中已经确定了带特别保护区域边界条件约束的最小暴露路径问题式(5)实质是一个带约束条件的泛函极值问题，也不能用求解泛函极值问题的变分法求其精确解[6~8]。

综合以上考虑和分析，本文用到了数学上求解泛函极值的一种间接方法——有限差分法的思路[5]。图2是对图1中的路径用有限差分法离散化以后的示意图，表示将区间进行等分，和对应的值组成的系列点坐标可以近似的表示路径。为方便描述，令，则可以表示为

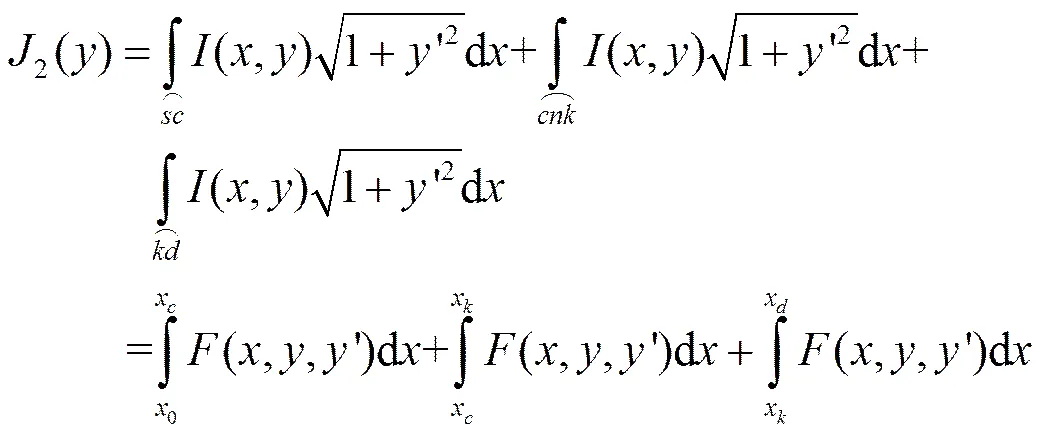
(6)

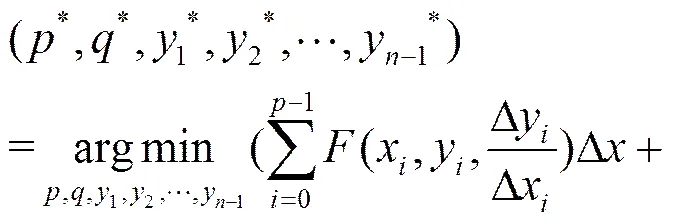
，(7)

4 混合人工蜂群求解算法

对最优化问题式(7)，在数学上有很多求解这类问题的确定性优化方法，如最速下降法[17]、插值法[18]、填充函数法[19]等，但这些方法都需要利用函数的导数等信息，只可用在性质较好的函数全局优化问题中，很难用于复杂的工程优化问题中。式(7)中要优化的目标函数的导数形式非常复杂，连续变量的维数比较高，因此不适于用经典确定性优化方法来求解最优化问题如式(5)。

相比以上提到的确定性优化方法，随机性优化方法对函数的要求较低，只需利用函数值，对目标函数的性质(可导性、连续性等)没有太多要求，可用于大多数优化问题的求解，适应面宽，适用于复杂的工程优化问题。

人工蜂群算法是近年由Karaboga提出的一种比较新的智能优化算法[20~23]，属于随机性优化方法中的一种。相比遗传算法、粒子群等其他智能仿生优化算法，人工蜂群算法中涉及到的参数更少，更加适合高维复杂问题的求解[24~26]，正适合用于最优化问题式(5)的求解。在人工蜂群算法中，一个蜜源位置就对应了一个优化问题的可行解，蜜源的花蜜数量就对应了相关问题的适应度函数值。这种算法模拟的是蜂群采蜜的行为，在蜜蜂采蜜时，整个蜂群中的蜜蜂会扮演3种角色：雇佣蜂、跟随蜂和侦查蜂。一般蜂群中的一半个体组成雇佣蜂，另一半个体组成跟随蜂。雇佣蜂负责搜寻可开采的蜜源并向其他蜜蜂提供蜜源信息。跟随蜂可以依据雇佣蜂提供的蜜源信息对蜜源进行进一步的搜索。当搜索到的蜜源质量在连续多次没有提高的时候，该蜜蜂个体就会转变成侦查蜂并在蜂巢附近进行新的初始化搜索。

虽然相比其他智能优化算法，基本的人工蜂群算法具有一定的全局搜索的能力（体现在雇佣蜂和跟随蜂搜索机制上）和跳出局部最优的能力（体现在侦查蜂搜索机制），但如果直接套用基本的人工蜂群算法求解最优化问题式(7)还是不会有非常好的求解效果，原因是式(7)不但维数高，而且由于有项的存在，式(7)还是一个高度非线性复杂的优化问题。直接运用人工蜂群算法的话，路径呈锯齿状跳跃现象，并且随着迭代次数的增加这样的现象没有明显改进，这表明基本的人工蜂群算法对最优化问题式(7)这样的高维非线性复杂优化问题缺乏很好的局部寻优能力。为解决这样的困难，本文设计了如下的混合人工蜂群算法，具体分析和设计过程如下。

4.1 适应度值函数

好的适应度函数才能引导算法向好的方向搜索，人工蜂群算法作为一种迭代搜索算法，良好的适应度函数形式的设计就显得非常的关键。对本文的优化问题式(7)，要优化的连续变量为，维数为−1。如果直接取式(4)表示的暴露度计算值作为适应度函数，为方便描述，记，这并不能很好地反映路径跳跃的程度，在跳跃比较大的线段上，感应强度值变化非常大，从而带来较大计算偏差；如果令表示点与之间的距离，则可以反映出路径锯齿状跳跃的程度，该值越小越好。理想情况是既希望折线段上的感应强度值变化尽可能得小，又希望跳跃现象尽可能得少。综合这2个因素的考虑，本文将适应度值函数修改为，其中，第一个求和项是取感应强度值在该线段上的上界代替的值，表示对第一个因素的惩罚，第二个求和项表示对第二个因素的惩罚，就是路径的长度，锯齿状跳跃程度越大，值也越大，乘以路径长度后得到的惩罚就越大。这样的设计思路是惩罚函数的设计思想，但和通常的惩罚函数方法相比可以减少对惩罚参数C的讨论，既考虑了暴露度值的拟合程度，又考虑了减轻路径锯齿状跳跃现象的发生，可以帮助个体向好的方向进化。

4.2 编码及约束条件的处理

在最优化问题式(5)中要优化的变量有−1维的连续变量，依据前面有关限制条件的分析，限制条件可以表示为:当时，满足。因此，要优化的变量除了外，还包括整数和对此可以采用混合编码,其中，和为1到−1之间的整数，且，连续变量可行域为当时，，其余的在感应区域内取值。

4.3 初始化及搜索方式

4.4 局部搜索算子

除了以上保证算法全局搜索能力的搜索方程的设计，还必须保证算法能具有局部探索寻优的能力。而对高维并且是高度非线性复杂的适应度值函数，由于惩罚项因子的存在，要设计出实际可用的局部搜索算子是非常困难的。对连续分量，当时，，考虑其余连续分量的局部最优值。为了找到这些连续分量局部最优值，避开对复杂的函数形式的分析，转而考虑简单函数形式，设计了如下的2种针对连续分量局部搜索算子，具体分析和步骤如下。

4.4.1 单维局部搜索

(10)

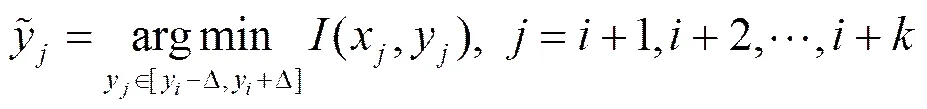
4.5 混合人工蜂群算法

综合以上设计的各个要点，针对带必经区域边界的最小暴露路径问题的多元最优化模型，本文设计的混合人工蜂群求解算法可以表示如下。

算法1 混合人工蜂群求解算法

1) 参数初始化。初始化种群大小，最大进化世代数，侦查蜂行为参数，维搜索参数中分量个数和搜索范围值。

3) 引领蜂搜索。对当前种群()中个体，选取个体适应度值最好的一半构成引领蜂群，其余的一半作为跟随蜂群。对每个引领蜂，随机选择引领蜂群中另一个个体，采用式(9)得到新的个体并计算新个体的适应度值，如果新产生的引领蜂个体比原个体好则替换原个体，否则保留原有的引领蜂个体。

4) 跟随蜂搜索。对跟随蜂中的每个个体，依据概率选择方式从新的引领蜂群体中概率选择较优个体，采用式(9)得到新的个体并计算新个体的适应度值，采取择优保留的方式组成新的跟随蜂群体。新的跟随蜂群体与引领蜂群体组成新的种群群体(+1)。

5) 侦查蜂搜索。对当前种群(+1)中的每个个体，判断是否超过行为参数值没有改进，如果经过代进化仍没有改进，则依据式(9)的方式重新对该个体进行初始化，并记录下当前种群的最优个体。

8) 终止条件。令=+1，如果当前进化世代数达到最大进化世代数，将记录的种群最优个体就作为全局最优解的近似解输出，否则跳转至3) 继续执行。

5 实验及结果

为了验证所设计算法能有效解决带保护区域的最小暴露路径问题，本文设计了一系列的仿真实验，包括保护区域外的传感器节点确定性分布和随机性分布，大规模节点分布等实验场景。

测试平台使用的计算机配置为：Pentium(R) Dual-Core CPU E5500 @ 2.8 GHz ,2 GB的RAM内存，Win XP(SP3)操作系统, 测试的仿真软件为Matlab 7.6.0。分别建立传感器节点确定性分布、随机性均匀性分布（包括大规模节点随机分布）等实验场景进行测试，节点的实验参数取值为，，无特别指出时，感应强度模型采用最大感应的感应强度模型。对于算法设计中的参数设置为：种群大小为50，最大进化代数为150~300，如果节点个数小于200，设置为150代，如果节点个数大于200，否则进化代数为300代。考虑曲线拟合的效果，平均每个传感器节点占用的编码长度至少为5比较合适，因此设置混合编码中中连续分量的编码长度取值为附近的一个整数，其中，为传感器节点个数；至于维局部搜索中的值的选取非常关键，如果该值太小，则多维局部搜索的效果会很弱；当时就变成了一维局部搜索，从而影响收敛的速度；如果该值太大，算法很容易陷入局部最优。通常，合适的取值为~的一个整数。

5.1 传感器节点确定性位置的布置场景及实验结果

对传感器节点位置确定性分布，设计了保护区域外传感器节点成等边三角形和正方形确定性布置实验场景，具体如下。

场景1 感应区域大小为10 m×10 m的正方形区域，保护区域为一条抛物线。在保护区域外确定性布置31个传感器节点，在保护区域内没有传感器节点的布置。在保护区域外的相邻传感器节点位置呈正方形关系，路径起点坐标(0,5)，终点坐标(10,3)，具体场景如图3(a)所示（在以后的场景中相同图例的含义不再重复叙述）。星号标识出传感器节点位置，加号和点虚线表示求解的最小暴露路径，在路径上每隔5个点标出了路径坐标点的编号（在以后的场景中相同图例的含义不再重复叙述），虚线标识出传感器节点对应的Voronoi图的边（通常称为Voronoi边），由于传感器节点成正方形分布，其对应的Voronoi边为正方形网格。算法中相关参数取值为：个体编码长度为56，群体大小为50，侦查蜂控制行为参数=10，维局部搜索的参数Δ=2,=10，最小暴露路径如图3(a)虚线所示，可以发现，除了在保护区域边界上的最小暴露路径部分，区域外的最小暴露路径几乎都是沿着Voronoi边前进，这和传统最小暴露路径问题中的结论[1,9,10]是一致的，求得的最终适应度值结果为93.382 4。图3(b)中的曲线分别给出了第1代(虚线带“×”)、第10代(点划线带“◆”)、第20代(双划线带“×”)、第40代(实线带“×”)、第75代(虚线带“+”)和第150代(实线带“+”)种群中最优路径随进化代数演变的过程(后续场景中的曲线图例与此图中的相同)。

(a) 节点布置及最终路径结果

(b) 最优路径进化过程

图3 场景1为31个传感器节点在区域外成正方形的确定性分布

场景2 在10 m×10 m区域范围内确定性布置30个传感器节点，相邻传感器节点位置呈正三角形关系，路径起点坐标(0,1.5)，终点坐标(10,6)。保护区域边界为一条抛物线。在保护区域内没有传感器节点布置，具体场景如图4(a)所示。由于保护区域外的传感器节点成正三角形的布置，相应Voronoi图为正六边形的网格。算法中相关参数取值为：个体编码长度为64，群体大小为50，侦查蜂控制行为参数=10，维局部搜索的参数Δ=1.851 6,=10。同样，求解得到的最小暴露路径几乎都是沿着Voronoi边前进，和传统最小暴露路径问题中的结论[1,9,10]一致，求得的最终适应度值结果为77.982 1。图4(b)中的曲线分别给出了第1代、第10代、第20代、第40代、第75代和第150代种群中最优路径随进化代数演变的过程。

(a) 节点布置及最终路径结果

(b) 最优路径进化过程

图4 场景2为30个传感器节点在区域外成三角形的确定性分布

以上2种场景求解得到的最小暴露路径在保护区域外都是沿着Voronoi边前进，这符合文献[1,9,10]中的结论。证实了在传感器节点位置确定布置性的场景下，本文中所设计的求取最小暴露路径的正确性和可靠性。

5.2 传感器节点均匀随机布置

为产生传感器节点均匀随机性布置的效果，本文通过对二维平面坐标的水平分量和竖直分量生成均匀随机数来产生每个传感器节点的位置坐标，总共模拟产生了如下4种场景。

场景3 在10 m×10 m区域范围内，特别保护区域为一条抛物线。在特别保护区域外确定性布置28个传感器节点，在特别保护区域内没有传感器节点的布置。起点坐标(0,4.1)，终点坐标(10,6.5)，群体大小为50，=56，总共进化代数为150，侦查蜂行为参数=10，搜索区间Δ=0.870 39，=10，最终适应度值结果为61.207 1，具体场景如图5所示。

场景4 在100 m×100 m区域范围内分别随机分布了160个传感器，起点坐标(0,40)，终点坐标(100,50)，群体大小为50，=121，总共进化代数为150，侦查蜂行为参数=10，搜索区间Δ=8.485 3，=20，最终适应度值结果为918.354 5，具体场景如图6所示。

场景5 在100 m×100 m区域范围内分别随机分布了200个传感器，起点坐标(0,40)，终点坐标(100,50)，群体大小为50，=121，总共进化代数为300，侦查蜂行为参数=10，搜索区间Δ=7.589 5，=24，最终适应度值结果为640.522 3，具体场景如图7所示。

场景6 在100 m×100 m区域范围内分别随机分布了400个传感器，起点坐标(0,40)，终点坐标(100,50)，群体大小为50，=181，总共进化代数为300，侦查蜂行为参数=10，搜索区间Δ=5.366 6，=32，最终适应度值结果为532.257 7，具体场景如图8所示。

(a) 节点布置及最终路径结果

(b) 最优路径进化过程

图5 场景3为28个传感器节点在区域外随机性分布

(a) 节点布置及最终路径结果

(b) 最优路径进化过程

图6 场景4为160个传感器节点在区域外随机性分布

(a) 节点布置及最终路径结果

(b) 最优路径进化过程

图7 场景5为200个传感器节点在区域外随机性分布

(a) 节点布置及最终路径结果

(b) 最优路径进化过程

图8 场景6为400个传感器节点在区域外随机性分布

以上4种传感器节点随机性布置的场景，节点规模逐渐增加，包括了小规模和大规模传感器节点随机性布置的情况，而且对应的模型式(5)的维数也逐渐增加，在场景4~场景6中的连续分量的维数达到了100以上，问题的维数（个体编码长度）已经非常高，设计的算法同样可以很好地解决问题的求解。在保护区域外，求解得到的最小暴露路径仍然是几乎沿着Voronoi边前进，这和文献[1,9,10]中的结论是吻合的。

5.3 算法收敛速度

考虑到篇幅限制，这里只给出了场景3和场景6的算法收敛效果。图9中的曲线分别表示对应场景3、场景6的最佳个体适应度值与进化代数进化的变化关系。可以看到图9中曲线都是快速地下降并收敛到平稳状态，证实了设计的算法收敛到全局最优解的速度很快，效率很高。另外，图9(a)中的曲线可以明显发现当种群进化到20代左右时适应度值增加后又开始快速地下降，由此可以看出算法确实具有跳出局部最优的能力。

(a) 场景3

(b) 场景6

图9 场景3和场景6最佳个体适应度值与进化代数进化的变化关系

6 结束语

原始最小暴露路径问题讨论的是从固定起点到达固定终点，路径中间环节没有任何的约束，本文提到最小暴露路径问题带有路径上的约束条件，这来自于客观条件（比如高温或环境恶劣或危险敏感区域）的限制无法达到某些区域，无法事先在这些区域内布置传感器节点，只能在其周围布置传感器节点来保护这个区域，移动目标也只能从固定的起点出发，到达这个敏感区域后只能沿着这个区域的边界移动，再到达固定的终点。本文所提出和讨论的问题是原始最小暴露路径的变种和延续。考虑到原有方法失效，将提出的问题抽象成优化模型，针对模型维数高、高度非线性难于求解的困难，设计的混合人工蜂群算法能有效地完成求解。以上讨论的带有限制约束的最小暴露路径还是在同构节点的前提下，在感知方式和感知距离不同的异构节点布置条件下，如何求解；以及根据找到的最小暴露路径结合节点的成本、异同构等特性进行下一步改善覆盖质量的传感器节点的再部署，这些都是本文后续进一步开展的工作。

[1] MEGERIAN S, KOUSHANFAR F, POTKONJAK M. Worst and best-case coverage in sensor networks[J]. IEEE Trans on Mobile Computing, 2005, 4(1):84-92.

[2] MEGUERDICHIAN S, KOUSHANFAR F, QU G. Exposure in wireless ad hoc sensor networks[C]//Proc of MobiCom 2001. Rome, Italy, c2001: 139-150.

[3] CLOUQUEUR T, PHIPATANASUPHORN V, RAMANATHAN P, et al. Sensor deployment strategy for detection of targets traversing a region[J]. Mobile Network. 2003, 8(4):453-461 .

[4] GELFAND I M, FOMIN S N. Calculus of Variationd[R]. Dove publisher, 2000, 1-14.

[5] AUBIN J P. Applide Functional Analysis(2nd)[R]. New York, John Wiley, 2000, 31-41.

[6] HRISTO N. DJIDJE V. Approximation algorithms for computing minimum exposure paths in a sensor field[J]. ACM Transactions on Sensor Networks, 2010, 7(23):1-23.

[7] HRISTO N, DJIDJEV L. Efficient computation of minimum exposure paths in a sensor network field[C]//DCOSS 2007. Santa Fe, NM, USA. c2007: 295-308.

[8] LIU L, ZHANG X, MA H. Minimal exposure path algorithms for directional sensor networks[C]//Global Telecommunications Conference. c2009: 1-6.

[9] MEGERIAN S, KOUSHANFAR F, QU G, et al. Exposure in wireless sensor networks: theory and practical solutions[J]. Wireless Network. 2002, 8(5): 443-454.

[10] VELTRI G, HUANG Q, QU G, et al. Minimal and maximal exposure path algorithms for wireless embedded sensor networks[C]//ACM Int’l Conf on Embedded Networked Sensor Systems (SenSys) Akyildiz IF, Estion D. c2003: 40-50.

[11] LIU D, NING P, LIU A, et al .Attack-resistant location estimation in wireless sensor networks[J]. ACM Transactions on Information and System Security, 2008, 11(4):1-39 .

[12] JINGFANG JIANG, GUANGJIE HAN, CHUNAN ZHU, et al. Secure localization in wireless sensor networks: a survey[J]. Journal on Communications, 2011, 6(6):460-470.

[13] 王福豹, 史龙, 任丰. 无线传感器网络中的自身定位系统和算法[J].软件学报, 2005, 16(5): 857-858.

WANG F B, SHI L, REN F. Self-Localization Systems and Algorithms for Wireless Sensor Network[J]. Journal of Software, 2005, 16(5): 857-858.

[14] WANG X, MA J J, WANG S. Prediction based dynamic power optimization in wireless sensor networks[J] . Sensors, 2007, 7 (3): 251-266.

[15] WANG L M, GUO Y B, ZHAN Y Z. Security topology control method for wireless sensor networks with node-failure tolerance based on self-regeneration[J]. Eurasip Journal of Wireless Communications and Networking, 2010,(1):1-11.

[16] 宋超, 刘明, 龚海刚, 等. 基于蚁群优化解决传感器网络中的能量洞问题[J]. 软件学报, 2009,20(10):2729-2743. SONG C, LIU M, GONG H G, et al. ACO-based algorithm for solving energy hole problems in wireless sensor networks[J]. Journal of Software, 2009,20(10):2729-2743.

[17] 李青剑, 王永, 陈绍青, 等. 一种方向优化最小均方算法[J]. 电子学报, 2014,36(6):1348-1354. LI Q J, WANG Y, CHEN S Q,et al. A direction optimization least mean square algorithm[J]. Journal of Electronics & Information Technology, 2014,36(6):1348-1354.

[18] 李彦, 王丽娜. 基于时间序列的时空插值算法改进研究[J] 2014,41(6):414-418. LI Y, WANG L N. Research of spato-temporal interpolation algorithm based on time series[J]. Computer Science, 2014,41(6):414-418.

[19] HONGWEI LIN, YUPING WANG, LEI FAN, et al. A new discrete filled funciton method for finding global minimizer of the integer programiming[J]. Applied Mathematics and Computation, 2012, 219: 4371-4378.

[20] KARABOGA D. An Idea Based on Honey Bee Swarm for Numerical Optimization[R]. Erciyes Univ, Kayseri, Turkey, Tech Rep-TR06, 2005.

[21] KARABOGA D, OZTURK C. Neural networks training by artificial bee colony algorithm on pattern classification[J]. Neural Network World, 2009,19(3): 279-292.

[22] KARABOGA D, OZTURK C. A novel clustering approach: Artificial bee colony (ABC) algorithm[J]. Applied Soft Computing, 2011, 11(1):652-657.

[23] OZTURK C, KARABOGA D, GORKEMLI B. Probabilistic dynamic deployment of wireless sensor networks by artificial bee colony algorithm[J]. Sensors, 2011,11(6):6056-6065.

[24] LEUNG Y W, WANG Y. An orthogonal genetic algorithm with quantization for global numerical optimization[J]. IEEE Transaction on Evolutionary Computing, 2001, 5(1):41-53.

[25] WANG Y P, DANG C Y. An evolutionary algorithm for global optimization based on level-set evolution and latin squares[J]. Transaction on Evolutionary Computing, 2007,11(5):579-595.

[26] SHANG Y W, QIU Y H. A note on the extended rosenbrock function[J]. Evolutionary Computing, 2006,14(1):119-126.

[27] SINGIRESU S, RAO S. Engineering Optimization: Theory and Practice[M]. New Jersy,John Wiley & Sons Inc, 2009.

[28] WOODFOR C, PHILLIPS C. Numerical Methods with Worked Examples: Matlab Edition(Second Edtion)[M]. Springer Dordrecht Heidelberg, 2011.

[29] WENYU S, YAXIANG Y. Optimization Theory and Methods: Nonlinear Programming[M]. New York: Springer Science Business Media, 2006.

New minimum exposure path problem and its solving algorithm in wireless sensor networks

YE Miao1,2,3,4, WANG Yu-ping1, DAI Cai1, WANG Xiao-li1

(1. School of Computer Science and Technology, Xidian University, Xi’an 710071, China; 2. College of Information Science and Engineering, Guilin University of Technology, Guilin 541004, China;3. Guangxi Cloud Security and Cloud Services Engineering Technology Research Center, Guilin University of Electronic Technology, Guilin 541104, China;4. College of Computer Science, Shaanxi Normal University, Xi'an 710062, China)

Due to the original minimum exposure path (MEP) problem in wireless sensor network without considering the constrained conditions for paths in practice, a new MEP problem with the request along a part of the boundary of the special protection area (BPA-MEP) was put forwand. As unable to set up the corresponding graph model, the classic methods (such as grid-based method and Voronoi-based method) in solving MEP problem would no longer work to BPA-MEP problem. To solve BPA-MEP problem, a optimization modelwith constraints as a highly nonlinear and higher dimensional problem was tailored and established and then taking the characteristic of the distribution of the sensor nodes, a hybrid artificial bee algorithm was proposed to solve this complex optimization model. The results of the proposed model and the designed algorithm, when implemented in many aspects, show that they can solve BPA-MEP problem effectively.

wireless sensor networks, minimum exposure path, protect area, hybrid artificial bee algorithm

TP393; TP212

A

10.11959/j.issn.1000-436x.2016007

2014-12-16；

2015-08-06

国家自然科学基金资助项目(No.61262075, No.61472297, No.61563012)；广西自然科学基金资助项目(No.014GXNSFAA118370)；广西自动检测技术与仪器重点实验室基金资助项目(No.YQ14204, No.YQ14104)；广西教育厅基金资助项目(No.YB2014148)

The National Natural Science Foundation of China(No.61262075, No.61472297, No. 61563012), The Natural Science Foundation of Guangxi (No.2014GXNSFAA118370), The Key Laboratory of Automatic Detecting Technology and Instruments of Guangxi (No.YQ14204, No.YQ14104), The General Programs of the Scientific Research Project of Guangxi Educational Committee (No.YB2014148)

叶苗（1977-），男，广西桂林人，西安电子科技大学博士生，桂林理工大学副教授，主要研究方向为网络计算、进化算法、人工智能。

王宇平（1961-），男，陕西西安人，西安电子科技大学教授、博士生导师，主要研究方向为人工智能、网络和工程设计中的优化方法、最优化理论、数据挖掘。

代才（1984），男，安徽阜阳人，西安电子科技大学博士生，主要研究方向为多目标优化、进化算法、人工智能。

王晓丽（1987-），女，山东潍坊人，西安电子科技大学讲师，主要研究方向为并行与分布式环境下的任务调度、工程优化等。