基于值域的GNSS姿态测量改进算法研究
李世杰,李治安,庞春雷,余永林,王勇
基于值域的GNSS姿态测量改进算法研究
李世杰,李治安,庞春雷,余永林,王勇
(空军工程大学信息与导航学院,陕西西安 710077)
针对基于值域的全球卫星导航系统(GNSS, global navigation satellite system)姿态测量方法没有考虑搜索域相关性而造成初始化时间长、搜索范围大的问题,提出了一种模糊度反约束值域搜索的改进方法。首先推导了固定基线长度条件下模糊度搜索空间,然后利用较小的2个搜索空间及其与俯仰角、航向角的关系重新确立了二维搜索域组合,最后根据值域搜索在基线二次残差最小情况下确定整周模糊度。实验结果表明,该算法充分利用了搜索域的相关性信息,减小了搜索空间,并将初始化时间缩短到40 s以内。
整周模糊度;姿态测量;值域;基线约束
1 引言
GNSS姿态测量的关键在于解算整周模糊度,目前常用整周模糊度的解算方法包括模糊度函数法[1]、最小二乘搜索法[2]、快速模糊度求解法[3]、最小二乘降相关平差法(LAMBDA, least-squares ambiguity decorrelation adjustment)[4]等,但由于GNSS多天线测姿具有基线短、长度固定已知等特点,也就决定了其整周模糊度的解算方法具有更多的附加约束条件,针对此特点,许多学者做了大量研究,如基线约束LAMBDA算法[5~7]、基于球面交点的模糊度函数法[8]、多约束条件下的最小二乘搜索法[9]等,这些方法大部分是在传统模糊度求解算法基础上进一步附加了基线约束条件,一定程度上提高了算法搜索效率,较好地满足了GNSS测姿的需要,但基线较短的特点还没有被充分利用。
文献[10]提出的基于值域GNSS姿态测量算法,充分利用了基线长度固定和较短的特点,给出了一种新的整周模糊度解算方法。该算法通过对值域,也就是基线俯仰角和航向角进行两步搜索,然后根据值域与整周模糊度的关系初步得到模糊度值,并在基线残差最小的情况下固定整周模糊度。与传统方法相比,该算法将对模糊度的直接搜索转化为对角度的搜索,方法更加简单。但是该算法采用了遍历搜索的方式,效率不高,且没有充分考虑搜索域的相关性,造成搜索范围大,初始化时间较长等问题。针对此问题,本文提出了一种模糊度反约束值域搜索的改进算法,充分利用了模糊度与俯仰角和航向角之间的关系以及搜索域的相关性,进一步缩小了搜索范围,缩短了初始化时间。
2 基于值域的GNSS姿态测量算法分析
2.1 算法模型
如图1所示,、分别为2个卫星天线位置,以为原点的东北天线坐标系ENU中,由到的基线矢量记为,基线长度、航向角、俯仰角分别记为、和;卫星的航向角、俯仰角分别记为和;为卫星与基线的航向角之差,即;为用户到卫星的单位矢量。
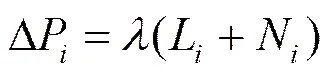
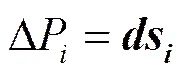
其中,
(3)
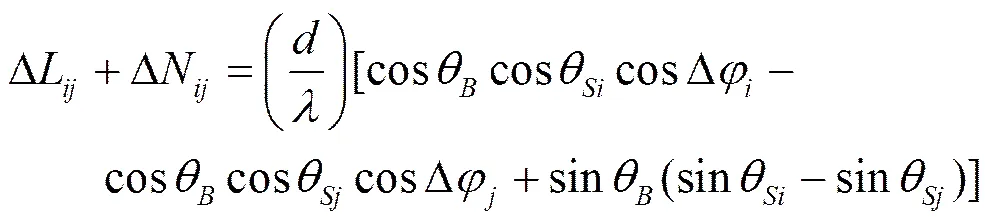
基于值域的姿态测量算法以式(4)为基础,首先进行搜索步长的理论推导,并以一定的搜索步长对俯仰角和航向角实施遍历搜索,然后利用式(4)解算相应的整周模糊度浮点解,经过处理后进一步反代求解基线长度,在基线残差最小的情况下固定整周模糊度。
2.2 算法分析
基于值域的姿态测量算法将对模糊度的搜索转化为对角度的搜索,与传统方法相比,算法更为简单。由搜索的具体过程可知,正确的模糊度组一定会对应一组特定的俯仰角和航向角组合,称之为最佳搜索组合,固定正确模糊度的过程即是确定最佳搜索组合的过程。
为了不漏掉正确的模糊度,必须进行遍历搜索,且每次搜索使模糊度的变化不能超过1周。粗搜索步长和可由式(5)确定[11]

然后再进一步以1°的步长进行精搜索。搜索次数相对较多,搜索效率还有待进一步提高。
理论上,对俯仰角和航向角进行遍历搜索,当搜索到最佳组合时,所解算出的基线残差应该最小。然而由于观测噪声等因素的影响,在短时间内,并不能保证最佳搜索组合所对应的基线残差与其他搜索组合所对应的残差有明显差别,也就是说,遍历搜索时较容易出现与最佳搜索组合相接近的角度组合,称之为伪组合,利用伪组合解算的基线残差往往也较小,因此还需要更多历元才能进一步消除伪组合,造成了搜索时间相对较长的现象。实际上,俯仰角和航向角之间是有一定约束关系的,若能充分利用其相关性信息,在搜索时减少伪组合个数,不仅可以减小搜索空间,而且可以缩短模糊度初始化时间,这就是本文的基本思想。
3 基于模糊度反约束值域搜索的改进算法
3.1 搜索域的确立
用矢量形式表示双差方程为
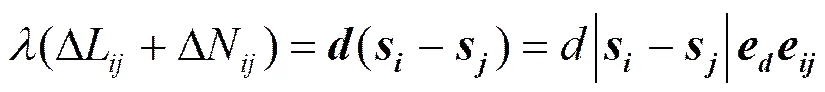
由式(6)可得
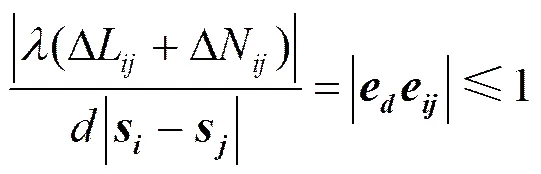
解不等式得
(8)
由于模糊度只能为整数,所以根据式(8)即可确定模糊度的整数取值范围,然后利用模糊度的整数范围及其与俯仰角、航向角之间的关系,进一步确定值域搜索范围。
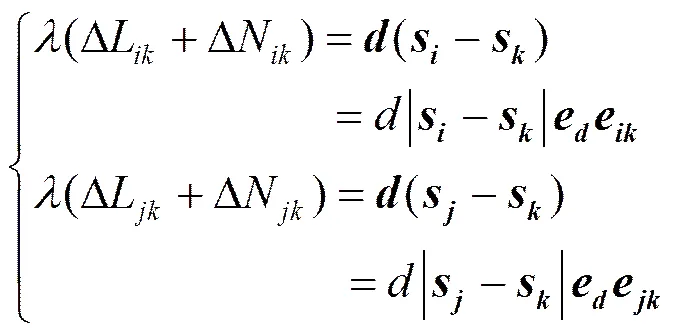
(10)
由式(9)和式(10)可得
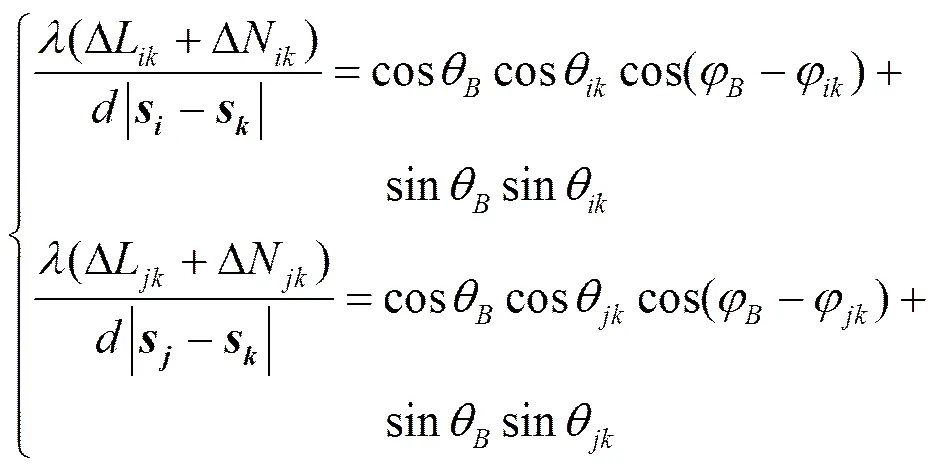
(12)
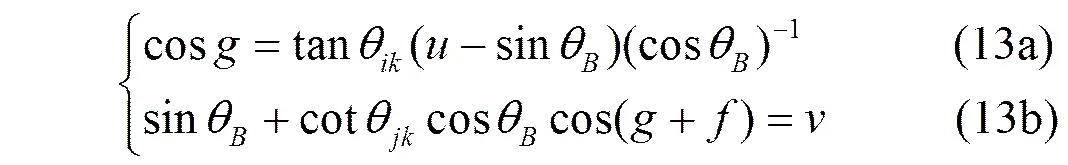
将式(13a)代入式(13b)进行整理,可得方程
(14)
其中,

(16)
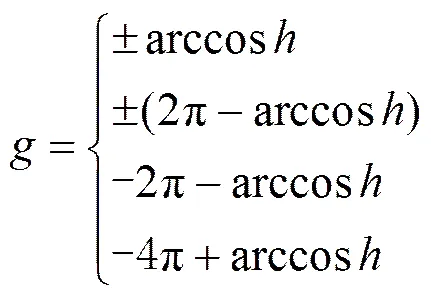
则得航向角的解为
(18)
由以上可知,每一组整周模糊度对应12组俯仰角和航向角解。为了检验解的正确性,可以根据俯仰角和航向角的实际取值范围剔除误解,再将剩余解代回到式(11)进行进一步检验。多次实验结果表明,根据每一组整周模糊度一般可以得1~2组俯仰角和航向角的解。利用模糊度的整数范围即可得到所有对应的俯仰角和航向角组合,并将其作为新的搜索空间,避免了对值域的遍历搜索,同时保证了每一组俯仰角和航向角都对应某一确定模糊度组,减小了搜索范围。可以看出,本文不是通过遍历搜索直接解算整周模糊度,而是先解算整周模糊度整数范围,然后根据其与俯仰角、航向角的关系,利用其中2个模糊度进一步约束值域搜索范围,再进行基于值域的搜索,因此,本文又称之为模糊度反约束值域搜索算法。该算法充分利用了搜索域的相关性,减少了伪组合的个数,能在较少历元情况下完成模糊度的正确固定,缩短了初始化时间。
3.2 整周模糊度的固定
在新的搜索空间内对所有俯仰角和航向角组合进行搜索,根据式(4),每一组角度值都可以解出一组整周模糊度的浮点解为

(20)

(22)
设历元个数为,取基线长度残差和最小的一组进行整周模糊度的固定,即满足

具体改进算法流程如图2所示,与原算法流程相比,改进算法在值域搜索之前进行了模糊度反约束处理,提高了搜索效率。
图2 改进算法流程
4 实验分析
4.1 实验条件
将2个型号为GPS-703-GGG的卫星天线分别固定在基线两端,基线长度为1.907 m,俯仰角和航向角分别为0.10°和229.15°。利用2个NovAtel OEM 628板卡进行数据采集。实验地点为学院操场,采样频率为1Hz,采集时间为10 min,卫星截止角为10°,得到可视卫星共有8颗,PRN分别为1、14、16、20、25、29、31、32。其中,PRN31卫星仰角最大,将其作为参考卫星与其他7颗卫星进行求差,共得到31-1、31-14、31-16、31-20、31-25、31-29、31-32这7组双差观测数据,分别利用基于值域搜索算法和改进算法进行实验。
4.2 实验结果及分析
根据本文算法,首先根据两组模糊度的搜索范围重新确立值域搜索范围,这里选取31-1、31-14两组观测数据进行计算,得到模糊度整数范围分别为8 388 602~8 388 619和6 626 611~6 626 640,进一步可得图3所示的待搜索角度分布。
本次实验中,待搜索的俯仰角和航向角有696组。如果直接采用基于值域的测姿算法,由式(7)可以得到5°的俯仰角搜索步长和4°的航向角搜索步长,所需粗搜索次数为次,精搜索次数为次,共需次搜索,明显高于本文算法所确定的搜索次数。事实上,改进算法所需的搜索次数主要由式(10)决定,还可以通过合理选择卫星使尽可能小,以进一步减小搜索范围,多次实验表明,改进算法所需的搜索次数一般在1 000次以下。
然后根据确定的搜索空间,利用本文算法进行整周模糊度的固定,结果如表1所示。为了验证算法的正确性,分别用LAMBDA算法、基于值域算法进行对比,计算出的整周模糊度值与本文算法一致。可以看出,采用基于值域算法和改进算法与采用LAMBDA算法所解得的模糊度值是相同的,都能正确固定整周模糊度。

表1 整周模糊度解算结果
本次实验中,直接采用基于值域算法所确定的最佳搜索组合为(0°,228°),但当搜索到(−5°,228°)、(5°,228°)、(0°,224°)、(0°,232°)、(−5°,224°)、(5°,232°)、(−5°,232°)、(5°,224°)等组合时,所解得的基线残差与由最佳搜索组合(0°,228°)所解得的残差在短时间内没有明显不同,也就是说出现了8个伪组合搜索域,需要更多的历元才能进一步判别正确的模糊度,造成了初始化时间相对较长,本次实验为146 s。若采用改进算法,所确定的最佳搜索组合为(0.078 1°,229.435 5°),由于改进算法充分利用了俯仰角和航向角之间的相关性,只出现了1个伪组合为(3.262 9°,229.023 7°),仅需要39 s即可判别出伪组合,固定到正确的整周模糊度值。
表2为本次实验中分别采用基于值域算法和改进算法所得实验结果对比。

表2 基于值域算法和改进算法实验结果对比
表2表明,相比原算法,改进算法可以显著减少搜索次数及伪组合个数,从而有效缩短初始化时间。
将整周模糊度反代到观测方程,根据姿态解算方法,分别计算出基线的长度、俯仰角和航向角,并与真实值对比,得到其误差曲线如图4~图6所示,均方根误差(RMSE, root mean square error)如表3所示。

表3 基线长度、俯仰角和航向角的RMSE
综上可以看出,采用本文改进算法,只需要搜索696次,即能在39 s内固定到正确的整周模糊度,得到精度较高的姿态信息,基线长度均方根误差在1cm内,俯仰角和航向角均方根误差都在0.1°范围内。
5 结束语
通过上述理论分析及实验结果表明:本文所提改进算法在基于值域姿态测量算法的基础上,利用卫星矢量和载波相位观测信息确立了模糊度搜索空间,然后利用其中2个搜索空间反约束值域搜索,减小了搜索范围,提高了搜索效率。在值域搜索过程中,充分考虑了俯仰角和航向角的相互约束关系,缩短了初始化时间,适用于基线约束条件下的GNSS实时姿态测量。
[1] XIA K W, ZHANG X Y, GAO J Y. Study on GPS attitude determination technology based on QPSO algorithm[C]//The 7th World Congress on Intelligent Control and Automation. Chongqing, China, c2008: 1869-1873.
[2] KIM D, LANGLEY R. An optimized least-squares technique for improving ambiguity resolution and computational efficiency[C]// ION GPS. Salt Lake City, USA, c1999: 1579-1588.
[3] FREI E, BEULTER G. Rapid static positioning based on the fast ambiguity resolution approach“FARA”, theory and first results[J]. Manuscripta Geodaetica, 1990, 15(6): 325-356.
[4] TEUNISSEN P J G. The leastsquares ambiguity décor relation adjustment: a method for fast GPS integer ambiguity estimation[J]. Journal of Geodesy, 1995, (70): 65-82.
[5] BUIST P, TEUNISSEN P J G, VER-HAGEN S. Instantaneous multi-baseli-ne ambiguity resolution with constraints[C]//International GPS/GNSS Symposium. Tokyo, Japan, c2008.
[6] PARK C. A baseline constrained LAM-BDA method for integer ambiguity resolution of GNSS attitude determination systems[J]. Journal of Control, Robotics and Systems, 2008, 14(6): 587-594.
[7] WANG B, MIAO L J, WANG S T,et al. A constrained LAMBDA method for GPS attitude determination[J]. GPS Solutions, 2009, 13(2): 97-107.
[8] 陈万通, 秦红磊, 丛丽, 等. 基于球面交点的AFM算法的误差分析与改进方法[J]. 电子与信息学报, 2010, 32(9): 2220-2225.
CHEN W T, QIN H L, CONG L, et al. Error analysis and improvement of the ambiguity function method based on the intersection point on sphere[J]. Journal Electronics and Information Technology, 2010, 32(9): 2220-2225.
[9] 任光辉, 茅旭初. 多约束条件的全球定位系统单频单历元短基线定向技术与实现[J]. 上海交通大学学报, 2014, 48(3): 335-340.
REN G H, MAO X C. Single frequency and single epoch short-baseline GPS orientation determination method and realization with multiple constraints[J]. Journal of Shanghai Jiaotong University, 2014, 48(3): 335-340.
[10] 庞春雷. 卫星导航进近着陆定位测姿关键技术研究[D].西安: 空军工程大学, 2013.
PANG C L. Key Technologies Research on GNSS Positioning and Attitude Determination for Approach and Landing System[D]. Xi’an, Air Force Engineering Uninviting, 2013.
[11] 庞春雷, 赵修斌, 余永林, 等. 加速度计辅助的双天线姿态快速测量方法[J].中国惯性技术学报, 2013, 21(6): 749-752.
PANG C L, ZHAO X B, YU Y L, et al. Method of fast attitude measurement based on two antennas assisted by accelerometer[J]. Journal of Chinese Inertial Technology, 2013, 21(6): 749-752.
[12] JIN W R, ZHAN X Q. Hybrid analytical resolution approach based on ambiguity function for attitude determination[J]. Journal of Zhejiang University, 2009, 10(7): 1038-1048.
Improved algorithm based on result zone for GNSS attitude measurement
LI Shi-jie, LI Zhi-an, PANG Chun-lei, YU Yong-lin, WANG Yong
(Information and Navigation College, Air Force Engineering University, Xi’an 710077, China)
The correlation of search zone was not included in the result zone algorithm for GNSS attitude measurement, which led to extended time for initialization and oversize range for searching, then an improved algorithm in which search zone was bounded by ambiguity was proposed in the following procedures. First, search space for ambiguity with the condition of fixed baseline length was deduced. Then combination of two dimensional search zone was established by the smaller two search spaces and their relations with heading and elevation angle. Finally the integer ambiguity was defined on the basis of result zone search with the minimal two-order residuals of baseline. The experiment reveals that the correlative information on search zone is fully exploited and the size of search space is reduced, with time for initialization reduced to less than 40 seconds.
integer ambiguity, attitude measurement, result zone, baseline constrain
TN967.1
A
10.11959/j.issn.1000-436x.2016023
2015-01-18;
2015-07-26
国家自然科学基金资助项目(No.61273049)
The National Natural Science Foundation of China (No.61273049)
李世杰(1990-),男,河南安阳人,空军工程大学硕士生,主要研究方向为卫星导航与定位。
李治安(1957-),男,陕西西安人,空军工程大学教授,主要研究方向为卫星及无线电导航技术。
庞春雷(1986-),男,安徽阜阳人,空军工程大学讲师,主要研究方向为卫星导航高精度定位及组合导航技术。
余永林(1974-),男,安徽阜阳人,空军工程大学副教授,主要研究方向为卫星及无线电导航技术。
王勇(1989-),男,山东潍坊人,空军工程大学博士生,主要研究方向为卫星导航与定位。

