基于用户模糊相似度的协同过滤算法

吴毅涛，张兴明，王兴茂，李晗



基于用户模糊相似度的协同过滤算法

吴毅涛，张兴明，王兴茂，李晗

(国家数字交换系统工程技术研究中心，河南郑州 450002)

针对离散评分不能合理表达用户观点和传统协同过滤算法存在稀疏性等问题，借鉴年龄模糊模型，提出了梯形模糊评分模型。该模型将离散评分模糊化为梯形模糊数，考虑了评分模糊性和信息量，通过梯形模糊数来计算用户相似度，据此设计了协同过滤算法，并证明了该算法是传统协同过滤算法在模糊域的扩展。实验表明，该算法在数据稀疏且用户数远多于项目数时性能突出，并且算法运行时间远小于传统协同过滤算法。

协同过滤；梯形模糊评分模型；模糊距离；模糊相似度

1 引言

电子商务的快速发展，使用户难以处理种类繁多的信息。而推荐系统已经被证明能帮助用户过滤无用信息，做出合理选择[1~3]。推荐系统根据使用内容不同，可分为基于内容推荐系统和协同过滤推荐系统[4]。

基于内容推荐系统主要利用用户的统计信息，如年龄、收入等，根据统计信息的关系进行推荐。协同过滤推荐系统根据评分信息寻找相似用户，寻找相似性大的前个邻居，根据邻居的评分进行预测。算法的关键是选取合理的相似性计算方法。传统算法大多采用余弦、Pearson等方法来计算用户相似度。协同过滤推荐系统易于处理数据并易于实现，是最成功和流行的推荐系统。

但目前协同过滤推荐系统大都使用离散评分[5]，用户在5评分等级集合{1,2,3,4,5}中选择对项目的评分。但用户对项目的喜好程度是非常模糊的，没有特定的标准，离散评分不能合理表达用户的观点，例如离散评分不能表达介于评分4和评分5之间的喜好程度[6]。并且协同过滤系统没有考虑评分信息量的问题，例如用户评分为1携带的信息量比用户评分为3携带的信息量要多。当评分矩阵稀疏时，协同过滤推荐系统的性能非常差。

为了合理表述用户间的关系，Yager[7]引入模糊理论，用模糊子集表示统计信息间的关系；Shamri等[8]提出了统计信息模糊模型，建立统计信息同模糊语言的映射关系，通过模糊语言来计算其相似度；Le[9]利用统计信息模糊模型，计算其统计信息相似度，再利用Pearson算法计算评分相似度，加权两部分得到最终相似度。在数据稀疏时，引入模糊理论的推荐系统精确度较高[10]，但忽略了评分的模糊性，只能片面表述用户观点，并且统计信息难于获得和处理，引入模糊理论的推荐系统适用范围很小。

上述研究表明，协同过滤推荐系统不能合理表达用户的观点，没有考虑评分信息量，且存在稀疏性等问题，引入模糊理论的推荐系统只能片面表述用户的观点，且系统的适用范围很小。

针对以上问题，本文借鉴统计信息模糊模型，提出了一种梯形模糊相似度模型，用模糊子集来表示用户评分间的关系，建立离散评分值和梯形模糊评分值的映射关系，将用户评分模糊化，并且考虑了评分的信息量，能合理表达用户观点。用梯形模糊评分进行用户相似度计算，设计了基于用户模糊相似度的协同过滤推荐（Fuzzy-UBCF）算法。实验结果表明，在数据稀疏且用户数远多于项目数时，准确度高，并且算法运行时间远小于传统协同过滤算法。

2 理论基础

2.1 模糊子集

引入模糊理论的推荐系统用模糊子集来表示统计信息间的关系，模糊子集是经典子集的推广，它是具有不分明边界的集合。Zadeh[11]对模糊子集的定义是：给定论域上的一个模糊子集，就是给定论域到区间[0,1]的一个映射，如式(1)所示。

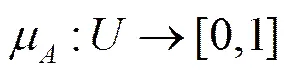
(1)

Chen[12]定义梯形模糊数为(,,,;)，、、、分别表示梯形的4个顶点，并且是实数；表示对模糊数的最大隶属度，0<≤1。梯形模糊数可以描述用户对项目的喜好程度，梯形模糊数如图1所示。

2.2 年龄模糊模型

Shamri[8]提出的年龄模糊模型描述了年龄同模糊语言的映射关系，如图2所示。

将年龄作为给定论域，以梯形隶属函数映射到模糊语言集中。相应的模糊语言集为{青年，中年，老年}，这种模型有以下优点。

1) 用模糊语言表示没有特定标准的统计信息，一个年龄可能映射到2个不同的模糊语言集，能合理地表述统计信息间的关系。

2) 在实际中，统计信息和模糊语言的隶属函数近似于正态分布，用梯形函数近似隶属函数比较合理。

3) 模型左右对称，用模糊梯形数表示模糊语言，计算简单。

年龄模糊模型是统计信息模糊模型的一种，但统计信息模糊模型只考虑了用户的部分信息，精确度较低，适用范围小。

3 基于用户模糊相似度的协同过滤推荐算法

本文用模糊子集来表示用户评分间的关系，建立了梯形模糊评分模型，将模糊理论引入协同过滤推荐系统中。

3.1 梯形模糊评分模型

本文在年龄模糊模型优点的基础上，对于一个5评分等级的集合，提出一种梯形模糊评分模型，如图3所示。

梯形模糊评分模型将满意度作为给定论域，用等腰梯形隶属函数将满意度映射到离散评分集中，满意度表示用户对项目的满意程度，满意度值越大，用户对项目越满意。梯形隶属函数的隶属度用信息量W来表示，信息量表示模糊数携带的信息的多少，信息量越大，模糊数携带的信息越多，信息量同模糊数出现的概率成反比，也就是同等腰梯形隶属函数的面积成反比，梯形面积越大，信息量越小。

本文定义了2个参数：和。和可以表示用户对一个项目的喜好程度，线段表示满意度区间对离散评分为1的确定度，在此范围内，离散评分和满意度是一一映射；线段表示满意度区间对离散评分为1的模糊度，在此范围内，离散评分和满意度不是一一映射。根据模型关系可得：≤0.25,≤。当不变，变大时，模糊评分数的确定度增加，适用于用户和项目关系较紧密的数据集，也就是稀疏度低的数据集；当不变，变小时，适用于稀疏度高的数据集。同理，当不变，变大时，适用于稀疏度高的数据集；当不变，变小时，适用于稀疏度低的数据集。

由模型左右对称，可知1=5，2=4。为了使W的值域为[0,1]，对W进行归一化处理，如式(3)所示。

(3)

其中，max(1,2,3)表示1,2,3中的最大值。

根据模型对称关系，得到5评分等级集合的梯形模糊评分值如式(4)所示。

(4)

3.2 模糊相似度计算

本文首次将Chen等[13]提出的梯形模糊数相似度计算方法引入推荐系统中，以此设计了用户模糊相似度计算方法，并证明模糊相似度是余弦相似度在模糊域的扩展。梯形模糊数相似度计算方法考虑了梯形模糊数的常规距离和重心距离，如式(5)所示。

其中，a为梯形的第个顶点，(,)为梯形的重心，如式(6)所示。

W为梯形的信息量，用来决定是否运用重心距离，定义如式(7)所示。

(7)

根据式(5)可以得出2个用户关于一个项目的相似度，加权所有项目的相似度就可以得到用户模糊相似度，如式(8)所示。

其中，代表用户和用户的共同评过分的项目的集合，R,i表示用户对项目的评分，为用户评分的项目数，上式还考虑了用户共同评分项目占总评分项目的比例，更能体现出用户和间的差异。

可以证明模糊相似度是余弦相似度在模糊域的扩展。

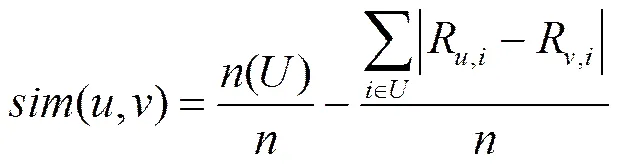
其中，为用户和共同评分的项目集合，()为集合中的项目数，为用户评分的项目数。即曼哈顿距离M，是指2个点在标准坐标系上的绝对轴距离总和，也就是欧氏距离在坐标轴上投影的距离总和，欧氏距离E表示2个点的实际距离，如式(10)所示。它们的关系如图4所示。

(10)

3.3 算法的流程

综合模糊相似度的计算，本节给出Fuzzy-UBCF对目标用户未知项目的预测评分集的流程。

算法 Fuzzy-UBCF (,)

输入：用户对项目的评分矩阵，用户邻居数。

Begin：

1) 用户相似度计算。

①根据式(5)计算目标用户和其他用户关于一个共同评分的项目的相似度(R,R)。

②根据式(8)得出目标用户和其他用户的模糊相似度()。

2) 产生推荐集

①挑选出相似度最高的个用户，作为邻居集。

②对近邻采用平均加权方法进行评分预测[14]，如式(12)所示。

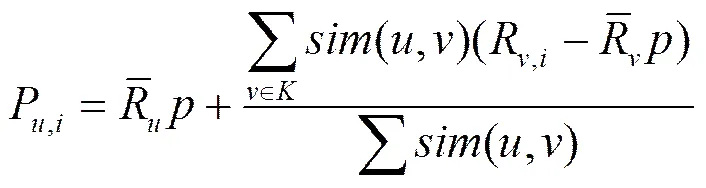
其中，P表示用户对项目的预测评分，()表示用户和用户之间的相似度，表示用户项目评分的均值，通过参数来减弱平均值对预测评分的影响，增加预测的模糊性，本文令=0.8。

我们家那时生活条件差，穿的都是自己家纺织的土布，添置一件新衣服后穿上要爱惜，新衣服平时不能穿，只是出门时穿一下。一件衣服大的穿后小的穿，直到烂得不能再穿了。出门时没有新衣服就是旧的也要洗干净，家里人很重视仪表和声誉。

输出：目标用户未知项目的预测评分集。

End

4 算法分析

4.1 基于用户模糊相似度算法正确性分析

传统相似性同用户向量的夹角是正相关关系，同用户向量的方向直接相关。模糊相似度同用户间的距离是负相关关系，同个体特征的维度，即同用户向量的长度直接相关。当用户向量的方向保持不变，长度增加时，传统相似度的值不变，而向量间的距离会变大，造成模糊相似度变小。所以项目数越多，模糊相似度的精确度越低。

传统的相似性计算，是从整体上计算用户差异，对单个用户对项目的评分值不敏感，项目越多，评分矩阵越密集，越容易分析其差异，故传统相似性适用于项目数多，且评分稀疏度低的数据集。而模糊相似性，分析的是用户评分的绝对差异，对单个用户项目的评分值敏感，用户越多，项目数越小，即用户项目比越大，越容易分析其差异，故模糊相似性适用于用户项目比大的评分矩阵。

虽然模糊相似度只考虑用户间的共同评分项目，一般来说共同评分项目很少，但本文将评分模糊化后，可以从项目较少的集合中获取更多信息，在评分矩阵很稀疏时也有很好的效果。故模糊相似度算法适用评分稀疏且用户项目比大的数据集。

协同过滤算法的时间开销主要在相似度计算中，本文只考虑相似性计算的运行时间，若用户的数量为，项目的数量为，余弦相似度算法的运行时间分析如表1所示。

表1 余弦相似度算法的运行时间分析

由于5远远大于1、2、3和4，故()=52=(2)，算法时间复杂度为(2)。

因为用户模糊相似性需要先计算(R,R)，即用户对单个项目的相似度，但只有5种评分，(R,R)只有25种可能值，可以提前计算出，这部分计算开销可以忽略不计。模糊相似度算法的运行时间分析如表2所示。

表2 模糊相似度算法的运行时间分析

由于6远远大于1、2、3和4，故()=62=(2)，算法时间复杂度为(2)。

虽然模糊相似度和传统相似度的算法复杂度都为(2)，但开销5需要进行3+1次乘法，2(−1)加法，2次开方和1次除法，开销6只需进行−1次加法和一次除法，故。Pearson相似度算法的运行时间远高于余弦相似度算法的运行时间，所以模糊相似性算法的运行时间远小于传统相似性算法。

5 实验与分析

5.1 数据集及实验环境

本文使用的是Netflix电影评分数据集(评分值为1~5的整数)，用于Netflix Prize比赛中。Netflix有2个不同大小的数据集，具体参数如表3所示。

表3 数据集的具体参数

本文实验环境为：win 7 操作系统，8 GB内存，Inter(R) Core(TM) i7-2600 CPU 3.40 GHz，实验程序使用 java 1.5语言开发。

5.2 评价指标

本文采用平均绝对误差作为算法性能的评价指标，如式(13)所示[15]。

其中，p为算法的预测评分，r为测试数据中的实际评分，为测试集中项目数目。越小，推荐精度越高。

5.3 比较算法及参数确定

本文采用以下2种算法作为对比算法。

余弦相似性的协同过滤算法(Cosine-CF)是协同过滤原始的经典算法。Pearson相似性的协同过滤算法(Pearson-CF)，在Cosine-CF的基础上进行改进，是目前应用广泛的算法，并且是基于用户的共同评分项目进行计算相似度，和本文提出的算法相同。

为了选取合理的和，本实验通过netflix_ 3m1k_split.txt文件，将Netflix_3m1k数据集中的95%作为训练集，5%作为测试集。将各组合的减去基准（0.735 0），在把差值扩大500倍，对比在不同和组合下大小，实验结果如图5所示。可得，当0.36≤+≤0.38时，值比较小，经过多次实验，本文选取=0.13,=0.23进行后续实验。

5.4 实验结果与分析

本实验中随机将80%的数据集作为训练集，20%的数据集作为测试集。为了减少随机分割数据集带来的误差，所有实验都进行10次，取平均值作为最终结果。

实验1 近邻数对算法精度的影响

当近邻数从5~50变化时，比较3种算法的大小。实验结果如图6和图7所示。

从实验结果可以得出以下结论。

1) 随着的增大，3种算法的精度都会提高，但算法复杂度也会增加。当>20时，算法精度趋于平稳，故本文选取=20进行后续实验。

2) 在Netflix_3m1k数据集中，随着邻居数的变化，Fuzzy-UBCF的精确度始终高于Cosine-CF，Cosine-CF的精确度始终高于Pearson-CF。

3) 在Netflix_5m3k数据集中，用户项目比减小，随着邻居数的变化，Fuzzy-UBCF的精确度略低于Cosine-CF，Fuzzy-UBCF的精确度始终高于Pearson-CF。

实验结果表明：Fuzzy-UBCF的算法在邻居数较少时，有较高的精度，因为将评分模糊化后，一个邻居所携带的信息更多。当用户项目比减少时，Fuzzy-UBCF的精确度就会下降，因为Fuzzy-UBCF考虑用户向量的距离，用户项目比越小，用户向量长度越长，精确度越低。当用户项目比减小时，Fuzzy-UBCF性能变差。

Pearson-CF的效果很差，是因为本数据集稀疏度很高，用户的共同评分项目很少，Pearson-CF没有发挥出自己的优势，在稀疏度低的数据集中，Pearson-CF的精度优于Cosine-CF。但Fuzzy-UBCF也是通过用户的共同评分项目进行计算，说明了Fuzzy-UBCF的优点。

实验2 稀疏度对算法精度的影响

在4.1节中，分析了Fuzzy-UBCF适用于评分矩阵稀疏的数据集，为了比较稀疏度对算法精度的影响，本实验在Netflix_5m3k数据集中，保证用户数和项目数不变，减少评分矩阵的稀疏度，当=20，比较3种算法的精度，实验结果如图8所示。

根据结果可以得出以下结论。

1) 随着稀疏度增加，可用信息减少，3种算法的精确度都会下降。

2) Pearson-CF的精度很差，不适用于稀疏度高的数据集。

3) 在稀疏度低于99.1%时，Fuzzy-UBCF比Cosine-CF稍差，但随着稀疏度的增高Fuzzy-UBCF的精确度高于Cosine-CF，而Cosine-CF随稀疏度变大，性能恶化很严重。

Fuzzy-UBCF将评分模糊化后，适用于用户和项目关系不明显的数据集，也就是适用于稀疏度高的数据集。

实验3 用户项目比对算法精度的影响

在4.1节分析中，本文得出Fuzzy-UBCF适用于用户项目比大的数据集，本实验在Netflix_5m3k数据集中，=20，保证用户和稀疏度不变，减少项目数来提高用户项目比，比较3种算法的精度，实验结果如图9所示。

从结果可以得出以下结论。

1) 随着用户项目比增加，3种算法的精确度都会下降。这是因为项目数减少，可用信息减少，精度会降低。

2) 随着用户项目比的增加，Fuzzy-UBCF的精度会优于传统的相似性算法。

可见，Fuzzy-UBCF适用于用户项目比高的数据集。在实际系统中，用户数是远远大于项目数的，并且数据集的稀疏度很高，所以Fuzzy-UBCF有很强的实用性。

实验4 算法运行时间

在4.2节中分析了Fuzzy-UBCF的运行时间，本实验来比较3种算法的运行时间，实验结果如图10所示。

可以得出，算法的运行时间关系为Pearson- CF>Cosine-CF>Fuzzy-UBCF。Fuzzy-UBCF的运行时间远小于传统的相似性计算方法。

实验5和参数对算法精度的影响

在3.1节中，分析了和组合的适用范围，本实验对此进行验证。在Netflix_5m3k数据集中，保证用户数和项目数不变，减少评分矩阵的稀疏度，为了避免出现大的误差，本实验只对参数进行微调。

当=0.23时，分别为0.125、0.13和0.135时，比较Fuzzy-UBCF的精度。由于3组参数的实验值很接近，为了便于比较，本文以=0.13、=0.23组合为基准，比较3种组合与=0.13、=0.23组合的差值。实验结果如图11所示。

从结果可以得出：当不变，变大时，适用稀疏度低的数据集；而不变，当变小时，适用于稀疏度高的数据集。

当0.13，分别为0.225、0.23和0.235时，比较Fuzzy-UBCF的精度。和上实验一样，比较3种组合与=0.13，=0.23组合的差值。实验结果如图12所示。

由实验结果可知：当不变，变大，适用于稀疏度高的数据集；当不变，变小时，适用于稀疏度低的数据集。

6 结束语

本文提出了一种梯形模糊评分模型，将离散的评分模糊化，考虑了评分信息量等因素，能更合理地表达用户的观点，并提出了一种基于用户模糊相似度的协同过滤算法，证明了Fuzzy-UBCF是传统协同过滤算法在模糊域上的扩展，通过与传统协同过滤算法比较，实验结果表明本文提出的算法有以下优点。

1) Fuzzy-UBCF更适用于评分矩阵稀疏的数据集。

2) Fuzzy-UBCF适用于用户项目比大的数据集，而现实的系统中用户项目比都很大，故Fuzzy-UBCF有很强的实用性。

3) Fuzzy-UBCF的算法运行时间远小于传统的协同过滤算法。

本文下一步计划，考虑用户的评分尺度，对梯形模糊评分模型进行优化，并优化模糊相似度中信息量计算部分，寻找到更合理的模糊相似度的加权方法，进一步提高算法精度。

[1] 荣辉桂, 火生旭, 胡春华, 等. 基于用户相似度的协同过滤推荐算法[J]. 通信学报, 2014,35(2):16-24. RONG H G, HUO S X, HU C H, et al. User similarity based couaborative fettering recommendation algorithm[J]. Journal on Communications, 2014,35(2):16-24.

[2] 李英壮, 高拓, 李先毅. 基于云计算的视频推荐系统的设计[J].通信学报, 2013,34(Z2):138-140. LI Y Z, GAO T, LI X Y. Design of video recommender system based on cloud computing[J]. Journal on Communications, 2013, 34(Z2): 138-140.

[3] 丁欣, 马严, 吴军. 适用于校园网的视频推荐系统的设计与实现[J].通信学报, 2013,34(Z2):175-179. DING X, MA Y, WU J. Design and implementation of a video recommendation system in campus network[J]. Journal on Communications, 2013,34(Z2):175-179.

[4] ZHAO Z D, SHANG M S. User-based collaborative-filtering recommendation algorithms on hadoop[C]//WKDD'10 Third International Conference on Knowledge Discovery and Data Mining. c2010: 478-481.

[5] YANG J M, LI K F. Recommendation based on rational inferences in collaborative filtering[J]. Knowledge-Based Systems, 2009, 22 (1):105-114.

[6] HUANG C K. Mining the change of customer behavior in fuzzy time-interval sequential patterns[J]. Applied Soft Computing, 2012, 12(3):1068-1086.

[7] YAGER R R. Fuzzy logic methods in recommender systems[J]. Fuzzy Sets and Systems, 2003, 136(2):133-149.

[8] SHAMRI M Y H, BHARADWAJ K K. Fuzzy-genetic approach to recommender system based on a novel hybrid user model[J]. Expert Systems with Applications, 2008, 35(3): 1386-1399 .

[9] LE H S. HU-FCF: a hybrid user-based fuzzy collaborative filtering method in recommender systems[J]. Expert Systems with Applications, 2014, 41(15):6861-6870.

[10] LUCAS J P, LUZ N, MORENO M N, et al. A hybrid recommendation approach for a tourism system[J]. Expert Systems with Applications, 2013, 40(9):3532-3550.

[11] ZADEH L A. Probability measures of fuzzy events[J]. Journal of Mathematical Analysis and Applications, 1968, 23(2):421-427.

[12] CHEN S H. Ranking generalized fuzzy number with graded mean integration[C]//The Eighth International Fuzzy Systems Association World Congress. c1999: 899-902.

[13] CHEN S J, CHEN S M. Fuzzy risk analysis based on similarity measures of generalized fuzzy numbers[J]. IEEE Transactions on Fuzzy Systems, 2003, 11(1):45-56.

[14] ZIEGLER C N, LAUSEN G. Analyzing correlation between trust and user similarity in online communities[J]. Lecture Notes in Computer Science, 2004:251-265.

[15] 朱郁筱, 吕琳媛. 推荐系统评价指标综述[J]. 电子科技大学学报, 2012, 41(2): 163-175.

ZHU Y X, LYU L Y. Evaluation metrics for recommender systems[J]. Journal of University of Electronic Science and Technology of China, 2012, 41(2): 163-175.

User fuzzy similarity-based collaborative filtering recommendation algorithm

WU Yi-tao, ZHANG Xing-ming, WANG Xing-mao, LI Han

（National Digital Switching System Engineering and Technological R&D Center, Zhengzhou 450002, China)

In order to reflect the actual case of human decisions and solve the data sparseness problem of traditional collaborative filtering recommendation algorithm, a trapezoid fuzzy model based on age fuzzy model was proposed. In this model, crisp point was fuzzified into trapezoid fuzzy number and the fuzziness and information of users’ grade was taken into account when calculating user’s similarity by trapezoid fuzzy number. Based on this model, the user fuzzy similarity-based collaborative filtering recommendation algorithm was designed. The algorithm was proved to be an extension of traditional collaborative filtering algorithm in fuzzy fields. The experimental results show that, the proposed algorithm performs better when implemented in the sparse dataset with more user than item, and its running time is much less than traditional collaborative filtering algorithm.

collaborative filtering, trapezoid fuzzy model, fuzzy distance, fuzzy similarity

TP393

A

10.11959/j.issn.1000-436x.2016024

2014-12-08；

2015-06-15

国家重点基础研究发展计划（“973”计划）基金资助项目（No.2012CB315901）；国家高技术研究发展计划（“863”计划）基金资助项目（No.2011AA01AA103）

The National Basic Research Program of China(973 Program)(No.2012CB315901), The National High Technology Research and Development Program of China (863 Program)(No.2011AA01AA103)

吴毅涛（1991-），男，陕西西安人，国家数字交换系统工程技术研究中心硕士生，主要研究方向为数据挖掘、社会化网络、推荐算法。

张兴明（1963-），男，河南新乡人，国家数字交换系统工程技术研究中心教授，主要研究方向为通信与信息系统、宽带信息网络等。

王兴茂（1989-），男，辽宁营口人，国家数字交换系统工程技术研究中心硕士生，主要研究方向为数据挖掘、用户行为分析、推荐算法。

李晗（1987-），女，河南汤阴人，国家数字交换系统工程技术研究中心工程师，主要研究方向为嵌入式系统。