稳定分布噪声下基于粒子滤波的双站伪多普勒定位方法

邱天爽，戚寅哲



稳定分布噪声下基于粒子滤波的双站伪多普勒定位方法

邱天爽，戚寅哲

（大连理工大学电子信息与电气工程学部，辽宁大连 116024）

传统的伪多普勒测向算法在高信噪比和高斯噪声环境下能较为精确地计算出到达方位角，但对于稳定分布噪声的顽健性较差。针对以上不足，提出了一种基于粒子滤波的双站伪多普勒定位方法。用粒子滤波对2个接收机的来波方位角进行联合估计，并通过非线性映射得到信源位置坐标估计，实现了方位角计算与双站定位的集成。仿真实验表明，当稳定分布参数为1.4（中等脉冲程度）时，所提方法在低信噪比下的顽健性要显著优于传统方法，在高信噪比时估计精度与传统方法相当；当信噪比为10 dB时，所提方法在的情况下定位精度远高于传统方法。

稳定分布噪声；粒子滤波；双站定位；伪多普勒；测向

1 引言

信源定位一直是通信和无线电监测技术领域的一个重点和难点问题。目前，信源定位的主要方法包括基于到达方位角（AOA, angle of arrival）和基于到达时间延迟（TDOA, time difference of arrival）2类。在基于AOA的定位方法中，主要算法包括ESPRIT[1]、MUSIC[2]等多通道、高分辨率的定位算法，尽管这类算法具有可靠的精度，但往往需要阵列天线等复杂设备，能耗及成本较高。

而基于伪多普勒测向算法[3~6]的双站定位方法则是一种设备简单、能耗小又能保证较高精度的单通道信源定位方法。最初的多普勒天线由一个围绕中心做机械圆周运动的全向天线构成，伪多普勒天线则是将若干根全向天线均匀排布在圆盘周边，通过依次接通每根天线的信号接收来模拟单根天线的机械圆周运动，使设备不再需要机械运动装置，且可以模拟高速转动，在增加设备稳定性的同时提高了测量精度。天线的圆周运动会给接收到的信号带来周期性的多普勒频移，并通过AOA的函数形式体现出来，通过一系列求解即可求出AOA。文献[5]系统介绍了传统多普勒测向和伪多普勒测向算法，并提出了一些改进方案。这种基于相位比较的传统测向方法在高斯噪声下具有可靠的精度，但对于对称α-稳定（SαS, symmetric alpha-stable）分布噪声会产生一定程度的退化。

粒子滤波算法[7]是近几年得到广泛重视和应用的一类理论算法，其基本思路是以某事件出现的频率来指代该事件的概率。该理论源于蒙特卡洛思想，形成于Gordon等[8]发表的论文。算法使用一组采样点(粒子)来近似表示目标状态的后验概率密度函数，每个粒子都配有一个权重，通过重要性采样剔除权重小的粒子，保留权重大的粒子，进而逐步逼近目标状态的真实后验概率密度函数，是一种顺序重要性采样方法(SIS, sequential importance sampling)。粒子滤波技术对于解决非线性、非高斯问题优势明显，适用于SαS分布噪声这类非高斯噪声下的参数估计问题。

针对传统伪多普勒测向算法的不足，在对SαS分布噪声下伪多普勒天线接收信号及基于AOA双站定位问题深入研究的基础上，本文提出了一种基于粒子滤波的双站伪多普勒定位方法，构造了以2个接收站的AOA为未知状态变量的非线性系统模型，并基于粒子滤波方法对2个接收站的AOA进行联合估计，再映射到真实坐标，实现了AOA计算与双站定位的集成。仿真实验结果表明，本文方法能在信噪比较低、特征指数α较小时保证较高的定位精度，对SαS分布噪声具有更强的顽健性，也易于扩展为3站乃至多站定位的情况。

2 信号噪声模型

2.1 伪多普勒天线接收信号模型

假设信源发出的AM调制信号如式(1)所示。

由天线的机械运动带来的多普勒效应实际上是对接收信号进行了相位调制，如式(2)所示，其中，为载波波长，为天线旋转的角速度，为来波方位角。

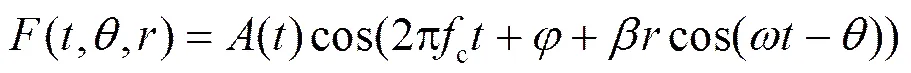
伪多普勒天线的接收信号模型其实是多普勒天线信号模型的量化，设为电子开关切换间隔，为天线总数，则每个内接收天线的位置是不变的，相临2根天线的角度相差，因此天线的等效角速度，则伪多普勒天线接收到的信号可用式(3)表示。

(3)

考虑到噪声的影响，则伪多普勒天线接收信号模型可用式(4)表示。

2.2 SαS分布

无线通信中的噪声主要是一些显著的大幅度脉冲(如雷电、多用户干扰等)，常表现出非高斯性[9]。Nikias等学者的研究成果表明，相比常用的高斯噪声模型，SαS分布模型能够更好地描述这类噪声[10]。SαS分布可由其特征函数表示[11]

3 定位方法

3.1 传统伪多普勒双站定位方法

图1(a)为使用多普勒天线[5]接收信号的示意，假设信源距天线足够远，则可认为信号为一平面波。Rx表示接收天线，Tx表示发射天线，天线圆盘半径为，一根全向天线绕圆盘中心做圆周运动，角速度为，时刻来波与天线夹角为。

减去载频带来的线性相位及初相后得到相位的多普勒项

(7)

伪多普勒天线是对多普勒天线的改进，在天线的圆周均匀排布若干根相同的全向天线，并通过电子开关以一定切换速率顺序接通每一根天线来模拟单根天线绕圆心的机械运动[5,12,13]。图1(b)为使用3根天线时的示意。此时定义为来波方向与时刻接通的天线(图中1号天线)之间的夹角。

(a) 多普勒天线

(b) 伪多普勒天线

图1 多普勒和伪多普勒天线接收信号示意

在测向算法上，伪多普勒算法与多普勒算法的原理是一样的，即先计算相位的伪多普勒项

图2所示为基于伪多普勒测向算法的双站定位系统的示意。

(a)

(b)

图2 伪多普勒双站定位系统示意

图2中Tx表示待定位信源的发射天线，Rx1和Rx2为2个型号和规格相同的伪多普勒天线，信号相对于2个天线的AOA分别为和。当Tx位于2站的图2(a)所示一侧时，有；当Tx位于2站的图2(b)所示一侧时，有；Tx位于2站所连直线上的情况属于可能性很小的特殊情况，此时2站AOA为0或π，可进一步根据接收信号强度等条件判断信源位置。

使用伪多普勒测向算法可以分别计算出每一个伪多普勒天线的AOA，进而可以画出一条接收天线位置到所估计信源位置的射线。通过2条AOA射线交于一点就可以得到信源位置的估计。因此最少用2个站就可以完成定位，也可以采用3站乃至多站来提高信源位置估计的精度。

3.2 基于粒子滤波的双站伪多普勒定位方法

对于基于AOA的双站定位任务，可以将2个站的AOA作为一个二元随机变量进行联合估计，待估参数可以表示为：，则可以得到时刻系统的状态方程为

SαS分布噪声会使信号相位在解卷绕后产生难以预测的相位模糊，这也是传统的基于相位比较的方法性能退化的主要原因，故若以信号相位作为观测值会严重影响粒子滤波过程中对权重的计算，因此本文采用信号的瞬时频率作为观测值。设求解2站接收信号瞬时频率的过程为，则观测方程为

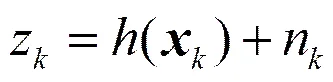
在粒子滤波算法中，最核心的一步就是计算每个粒子的重要性权重。假设已经获得上一时刻的粒子集(表示第个粒子，为粒子总数)及其对应的重要性权重，则当前时刻的粒子可以通过状态模型采样获得[15]

而当前时刻粒子的重要性权重可通过式(12)计算。

(12)

将其代入式(9)，得到重要性权重的更新公式

(14)

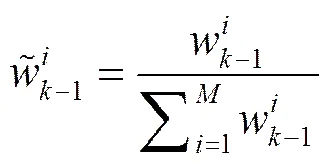
由于SαS分布不具有封闭的表达式，文献[14]提出可以对SαS分布进行高斯近似，进而可以得到粒子与观测值的似然度分布

(16)

其中，为高斯近似的标准差。

经过粒子重采样[16,17]后就可以得到后验分布的近似

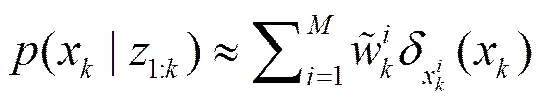
本文提出的结合伪多普勒测向算法的粒子滤波算法具体步骤如下。

3) 根据式(13)计算每个粒子与观测值的似然度。

4) 根据式(11)计算重要性权重并根据式(12)进行权重归一化。

END WHILE

(19)

与实际空间的位置坐标为一一映射关系，因此得到了即得到了信源的位置坐标。

4 仿真实验

4.1 实验条件

如图4所示，设定A、B这2个接收站的中点为直角坐标系原点，2站连线为X轴，A站坐标为(−2,0)，B站坐标为(2,0)，待定位信源坐标为(3,3)，设单位均为km。根据文献[18]提出的天线孔径及天线元数量的选择标准，本文仿真实验使用的伪多普勒天线半径为0.25 m，圆周上均匀分布6根完全相同的全向天线，天线切换频率为24 kHz。信源发射AM调制信号，中心频率为425.5 MHz，接收机接收信号的中频为120 kHz，带通采样频率为360 kHz。

4.2 实验结果及分析

分别采用本文方法与文献[5]的相位比较法进行了伪多普勒测向定位的仿真实验，并进行了对比分析。仿真实验中，SαS分布噪声的值为1.4，本算法的粒子数量设为800。图5所示为定位精度随GSNR变化的曲线。定位误差采用估计位置坐标与真实位置坐标间的欧式距离来表示，单位为km。由于AOA与位置坐标之间为非线性映射，导致相同GSNR下每次实验结果也会差异较大，因此本文对每个GSNR取100次实验结果的平均值作为该GSNR下的定位精度。

图5 定位误差随广义信噪比的变化曲线

图6所示为2种方法的定位精度随SαS分布噪声参数的变化曲线。本方法的粒子数量为800，GSNR为10 dB。每个点的数据同样为100次实验结果的平均值。从图中可以明显看出当时，相位比较法性能严重退化，相比之下，本文方法在范围内都能保证1 km左右的精度，表明本文方法对服从SαS分布的脉冲噪声有较强的顽健性。不过当，即噪声分布退化为高斯分布时，相位比较法的定位精度很高，这主要是由于相位比较法是直接求解AOA的解析解，在信道噪声环境理想的情况下能够很接近真实解，而粒子滤波是基于蒙特卡洛思想，毕竟频率分布无法完全代表概率分布，从而对估计精度造成一定影响。

图7为本文算法定位误差随粒子数量的变化曲线，值设定为1.4，GSNR设定为20 dB，取100次实验结果的平均值。可以看出定位误差随着粒子数量的增加有稳定下降的趋势，因此可以通过增加粒子数量来改善本文方法的估计精度。

本文仿真实验使用的计算机主要硬件配置为Intel(R) Core 2 Duo CPU T6500 2.10 GHz，2 GB内存，操作系统为Windows 8.1 32 bit。图8所示为算法运行所用时间随粒子数量的变化曲线。当粒子数为1 000时运行时间为7 s左右，基本满足一般定位任务的速度要求。

5 结束语

针对稳定分布噪声下基于AOA的信号源定位问题，本文提出了一种基于粒子滤波的双站伪多普勒定位方法，将2个接收站的AOA作为一个二元随机变量，使用粒子滤波对其进行联合估计，实现了AOA计算与双站定位的集成。仿真实验表明，相比基于相位比较算法的定位方法，本方法能在信噪比较低、特征指数较小时保证较高的定位精度，对稳定分布噪声具有更强的顽健性。适当增加粒子滤波使用的粒子数量还可以进一步提高定位精度。本文的研究成果也可以方便地扩展到3站乃至多站定位的情况，具有很高的实用价值。

[1] ROY R, KAILATH T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J]. Acoustics, Speech and Signal Processing, IEEE Transactions, 1989, 37(7): 984-995.

[2] SCHMIDT R O. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276-280.

[3] PEAVEY D, OGUMFUNMI T. The single channel interferometer using a pseudo-doppler direction finding system[C]//Acoustics, Speech, and Signal Processing, ICASSP-97, 1997 IEEE International Conference. c1997: 4129-4132.

[4] SALLAI J, VOLGYESI P, LÉDECZI Á. Radio interferometric quasi Doppler bearing estimation[C]//Information Processing in Sensor Networks, IPSN 2009, International Conference. c2009: 325-336.

[5] BABJAK B, SZILVASI S, VOLGYESI P. On accurate, low-complexity quasi doppler based localization[C]//The Third International Conference on Digital Information and Communication Technology and its Applications (DICTAP2013). c2013: 85-92.

[6] SHARAWI M S, ALOI D N. Characterizing the performance of single-channel pseudo-Doppler direction finding systems at 915 MHz for vehicle localization[J]. International Journal of Communication Systems, 2011, 24(1): 27-39.

[7] KLAAS M, DE FREITAS N, DOUCET A. Toward practical N2 Monte Carlo: the marginal particle filter[J]. arXiv preprint arXiv: 1207. 1396, 2012.

[8] GORDON N J, SALMOND D J, SMITH A F M. Novel approach to nonlinear/non-Gaussian Bayesian state estimation[J]. IEE Proceedings F (Radar and Signal Processing), IET Digital Library, 1993, 140(2): 107-113.

[9] 赵春晖, 杨伟超, 马爽. 基于广义二阶循环统计量的通信信号调制识别研究[J]. 通信学报, 2011, 32(1): 144-150.

ZHAO C H, YANG W C, MA S. Research on communication signal modulation recognition based on the generalized second-order cyclic statistics[J]. Journal on Communications, 2011, 32(1): 144-150.

[10] TSIHRINTZIS G A, NIKIAS C L. Fast estimation of the parameters of alpha-stable impulsive interference[J]. Signal Processing, IEEE Transactions, 1996, 44(6): 1492-1503.

[11] SONG A, TONG Z, QIU T. A new correntropy based TDE method under α-stable distribution noise environment[J]. Journal of Electronics (China), 2011, 28(3): 284-288.

[12] WECKSTROM M T. Doppler direction finder and method of location using doppler direction finder[P]. U S Patent 6,268,829. 2001-7-31.

[13] WHITLOCK R. High gain pseudo-Doppler antenna[C]//Loughborough Antennas & Propagation Conference. c2010: 169-172.

[14] 邱天爽, 夏楠, 李景春, 等. 稳定分布噪声下基于高斯近似粒子滤波的干扰源定位算法[J]. 信号处理, 2012, 28(9): 1248-1253.

QIU T S, XIA N, LI J C, et al. An interference localization algorithm based on Gaussian approximation particle filtering with stable distribution noise[J]. Signal Processing, 2012, 28(9): 1248-1253.

[15] ZHONG X, PREMKUMAR A B, MADHUKUMAR A S. Particle filtering for acoustic source tracking in impulsive noise with alpha-stable process[J]. Nor Jornal, 2013, 13:589 - 600.

[16] 冯驰, 王萌, 汲清波. 粒子滤波器重采样算法的分析与比较[J]. 系统仿真学报, 2009, (4): 1101-1105.

FENG C, WANG M, JI Q B. Analysis and comparison of resampling algorithms in particle filter [J]. Journal of System Simulation, 2009, (4): 1101-1105.

[17] 于春娣, 丁勇, 李伟, 等. 一种基于改进重采样的粒子滤波算法[J]. 计算机应用与软件, 2013, 30(2): 296-299.

YU C D, DING Y, LI W, et al. A article filtering algorithm based on improved resampling[J]. Computer Applications and Software, 2013, 30(2): 296-299.

[18] 莫景琦. 对一些无线电测向技术问题的研讨[J]. 中国无线电, 2007, 2:20.

MO J Q. Discussion on several radio direction finding technologies[J]. China Radio, 2007, 2:20.

Dual-station pseudo-Doppler localization method based on particle filtering with stable distribution noise

QIU Tian-shuang, QI Yin-zhe

(Faculty of Electronic Information and Electrical Engineering, Dalian University of Technology, Dalian 116024, China)

Traditional pseudo-Doppler bearing estimation algorithm could accurately calculate the angle of arrival (AOA) with Gaussian noise and high signal to noise ratio (SNR), but it was less robust with stable distribution noise. To overcome these shortcomings, a dual-station pseudo-Doppler localization method based on the particle filtering was proposed. The method employed particle filtering approach to jointly estimate the AOA of both stations, then applied a non-linear mapping to acquire the source location, forming an integration of AOA calculation and dual-station localization. Simulations demonstrate that when the characteristic exponent of the stable distribution is in a medium degree, for example, the proposed method is much more robust than the traditional method in low SNR circumstances, while maintaining the estimation accuracy of the traditional method when SNR is high. When SNR equals 10 dB, the positioning accuracy of the proposed method is much higher than the traditional method with.

stable distribution noise, particle filtering, dual-station localization, pseudo-Doppler, bearing estimation

TN911.72

A

10.11959/j.issn.1000-436x.2016004

2014-12-29；

2015-05-16

邱天爽，qiutsh@dlut.edu.cn

国家自然科学基金资助项目（No.61139001, No.61172108, No.81241059）；国家科技支撑计划基金资助项目(No.2012BAJ18B06-04)

The National Natural Science Foundation of China (No.61139001, No.61172108, No.81241059), The National Key Technology R&D Program (No.2012BAJ18B06-04)

邱天爽（1954-），男，江苏海门人，大连理工大学教授、博士生导师，主要研究方向为信号与信息处理。

戚寅哲（1990-），男，辽宁沈阳人，大连理工大学硕士生，主要研究方向为通信信号处理和信号源定位。