基于改进FastICA算法的入侵检测样本数据优化方法

杜晔，张亚丹，黎妹红，张大伟



基于改进FastICA算法的入侵检测样本数据优化方法

杜晔，张亚丹，黎妹红，张大伟

（北京交通大学计算机与信息技术学院，北京 100044）

为更好实现对入侵检测样本数据的优化处理，提出了一种改进的快速独立成分分析(FastICA)算法，采用基于加权相关系数进行白化处理以减少信息损失，并优化牛顿迭代法使其满足三阶收敛。对算法进行了细致描述，分析了算法的时间复杂度。实验结果表明，该方法可有效减少数据信息损失，具有迭代次数少、收敛速度快等优点，可有效提高入侵检测样本数据的优化效率。

入侵检测；快速独立成分分析；数据优化；牛顿迭代法

1 引言

随着信息技术的发展，网络已经渗入到人们工作、生活的方方面面，带来了巨大的便利。但随之而来的是，针对网络的攻击也层出不穷，入侵计算机系统的手段方法不断增加，已呈智能化与协同性发展。根据国家互联网应急中心（CNCERT）发布的《2013年我国互联网网络安全态势综述》[1]，2013年CNCERT监测发现境内有1.5 万台主机被APT木马控制，6.1万个网站被境外通过植入后门实施控制，1 090万余台主机被境外控制服务器控制。网络攻击事件的频繁发生，不仅对广大网民利益造成了影响，更对社会经济和国家安全造成威胁和挑战。为了保护系统资源，作为一种积极、主动的动态防护技术，入侵检测的研究与发展就愈发显得重要。

1980年，John Anderson的报告“Computer security threats monitoring and surveillance”[2]被认为是最早涉及到入侵检测领域的文献。他将入侵企图定义为故意地、非授权地试图访问信息、修改信息、致使系统不可靠或不可用。由于互联网的资源共享原则，很难识别非授权用户，攻击者可以利用大量网络主机来占用网络的关键资源使网络服务质量显著降低，即发生入侵攻击[3]。入侵检测的作用就在于及时地发现各种攻击以及攻击企图，并做出反应[4]。入侵检测技术可以分为误用入侵检测和异常入侵检测。误用检测通过预先精确定义的入侵模式进行检测，如果入侵者攻击方式恰好匹配上检测系统中的模式库，入侵行为即被检测到。异常检测认为入侵活动是未知的，是异常活动的子集。任何对正常行为模式的偏离达到一定程度时，都认为是入侵事件的发生。

由于入侵检测需要对大量的系统实时数据进行分析和处理，例如基于主机的检测需要对CPU、内存、进程等参数进行分析，且通常这些数据是高维的，这必将会造成维数灾难，增加入侵检测系统分析的复杂度、时效性。因此，在进行入侵检测前有必要对数据进行优化处理。它不仅可以降低问题规模，减小问题复杂度，而且可以去除不相关和冗余的数据，从而增加检测的准确度。

本文提出了一种改进的FastICA算法，采用基于加权相关系数的白化处理过程有效减少数据精简带来的信息损失，通过改进牛顿迭代法实现3阶段收敛，以减少迭代次数，提高收敛速度。

2 相关工作

入侵检测通常需要收集大量的历史数据，而这些数据往往是高维的且具有相关性、冗余性，这不仅会导致入侵检测效率低，而且会影响检测正确率。因此，需要对数据进行预先优化处理。

Derek Smith[5]提出结合贝叶斯网络和主成分分析（PCA）对数据进行优化的方法，利用贝叶斯网络去除和入侵检测无关的特征属性以及各属性间的相关性，然后利用PCA进一步降维。文献[6]利用互信息去除和属性有最大相关性的属性，利用PCA对剩余的属性特征进行降维处理。上述2种方法都利用了PCA，而PCA只能去除各属性间的相关性并不能保证各属性相互独立。文献[7]采用基于步进指标搜索算法和指标空间分离技术进行云指标提取，得到最能刻画云行为和健康状况的最大关联性标准和最小冗余度标准，然后使用最小封闭球体将云指标数据点从数据空间映射到内核空间进行降维。Husanbir[8]提出把数据优化分为2部分，利用MI提取出最能表示计算机行为的特征属性，对于仍包含多个特征的集合，通过空间分离技术进一步提取特征，完成数据的优化处理。由于以上2种方法都引入了空间分离技术，这将加大计算过程的复杂性。文献[9]提出了一种关于特征的分层关系来表示它与异常的相关程度，并利用EdgeRank算法确定对某个特定故障起关键作用的特征属性。文献[10]提出了一种MRPC Selection算法，对每一类故障选择最相关主成分集合，并且为了适应动态性引入神经网络计算主成分。以上2种方法都是针对每一类故障找到最相关的主成分，但若收集的故障种类覆盖度不全则会直接影响到主成分的完备性。文献[11]提出一种基于因子分析的数据降维方法，从研究指标相关矩阵内部的依赖关系出发，把信息重叠、具有错综复杂关系的变量归结为少数几个不相关的综合因子。但在计算因子得分时，采用的是最小二乘法，该方法对于一些情况会失效。文献[12]介绍了非负矩阵分解降维方法，将大矩阵分解为2个小矩阵，使这2个小矩阵相乘后能还原到大矩阵，且分解后的矩阵都是非负的。但该方法计算过程存在许多局部最小点，存在陷入局部最优的情况。

本文提出一种改进的FastICA算法并将其应用于入侵检测样本数据优化阶段，不仅可以保证各属性相互独立且不会陷入局部最优的情况，同时可有效减少信息损失，加快收敛速度。

3 改进的FastICA算法

3.1 FastICA简介

独立成分分析最早应用于盲源信号分离（BBS），起源于“鸡尾酒会问题”，近年来已应用于多个领域，如自动化识别[13]、入侵检测[14]等。目前已形成基于高阶统计量算法、基于信息的优化算法、快速定点算法，并从定点算法中派生出了目前广泛使用的FastICA算法。

FastICA的求解过程主要包括数据预处理和独立成分提取。

1) 数据预处理

通常情况下，收集的数据具有相关性，需要对其进行白化处理以去除各观测变量之间的相关性，以简化后续独立成分的提取过程。对于观测向量，对其进行线性变化得到新的向量，使。此过程通常由主成分分析（PCA）完成。

2) 独立成分提取

确定目标函数后，需要选择学习算法来求解目标函数。FastICA采用基于固定点迭代的定点算法，定点迭代算法收敛速度更快、更可靠。FastICA利用了牛顿迭代法求解式（1）为

(2)

最后可得的迭代公式为

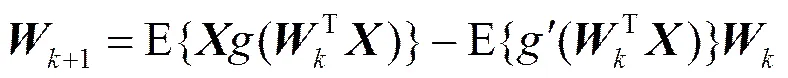
3.2 改进的FastICA算法描述

3.2.1 基于加权相关系数PCA算法的白化处理

独立成分提取前要对数据进行中心化和白化处理，这样不仅可以去除属性间的相关关系，还可以降低数据维度，减小噪声。传统的白化处理利用了基于协方差的PCA算法，协方差是有量纲的统计量，它受2个相关变量量纲的影响。而本文收集的性能数据各属性的量纲不同，所以传统方法并不可行。此外，白化处理过程会降低数据维度，带来一定的信息损失。要保证入侵检测的正确率，信息损失一定要尽可能少。基于以上2点，本文采用基于加权相关系数的PCA算法进行白化处理。

首先，相关系数是无量纲的统计量，不受属性量纲的影响。其次，引入权值，可以将不同属性置于不同地位。因为不同属性对于异常检测的贡献率是不同的，所以需要区别对待。根据变量方差的含义，定义如下权值

由此，得到加权相关系数

(5)

3.2.2 算法描述

由于在求解目标函数时采用了牛顿迭代法，而牛顿迭代法在单根情况下仅能达到2阶收敛，导致迭代次数多，收敛速度慢。对此，本文提出一种改进的牛顿迭代法，如式（6）所示，实现3阶收敛，减少迭代次数，加快收敛速度。

由文献[15]中的引理1可以证明式(6)为3阶收敛。由此来求解式(1)。

(8)

同理可得

(10)

所以，得到的迭代式如下

得到的整个迭代过程如下。

step2 进行如下计算

改进的FastICA算法流程如图1所示。

3.3 时间复杂度分析

改进的白化处理过程引入了基于加权相关系数的PCA，需要计算每个属性变量的方差

假设数据集有个样本，个属性变量，则时间复杂度增加()。

由于每次迭代的计算量可能增加，改进后的牛顿迭代法是否真正减少计算量不只取决于收敛阶。牛顿迭代法的效率指数，可用来判定改进的方法是否真正减少了计算量，效率指数越高说明收敛效率越高。效率指数可做如下定义[16]。

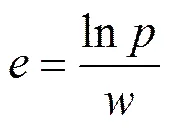
其中，是收敛阶数，是每次迭代的计算量。由式（2）和式（6）可得2种方法的效率指数如表1所示。

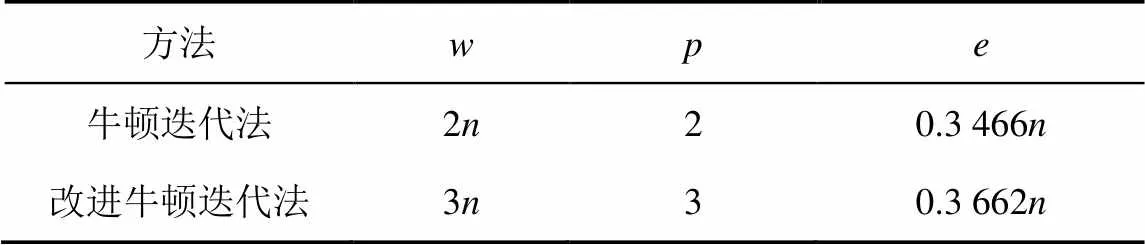
表1 2种方法效率指数对比

如表1所示，改进后的牛顿迭代法在提高收敛阶的同时，提高了迭代序列的效率指数，可有效地提高收敛速度。

4 算法应用与性能分析

4.1 数据特征采集

使用第三方监测工具sysstat在3台机器上进行数据收集，每5 min记录一次，共79个特征指标[17]，包括CPU使用情况、进程创建、任务转换活动、内存利用率、I/O切换、内存和交换空间的使用、网络活动等。测试数据集共采集64 MB的样本数据，表2列举了主要的指标属性。

首先，对收集的数据进行预处理。若某个时间点的数据未成功记录，则用相邻2个时间点的数据的平均值进行填充。对收集的数据进行观察，若收集过程中某个属性的值一直未发生变化，则说明对后面的异常检测没有贡献，可以直接去除。经筛检，最终保留%user、%system、%iowait、%idle、fault/s、kbmemfree、%memused、kbbuffers、kbswpfree、kbswpused等17个属性。

4.2 性能测试与分析

4.2.1 白化处理

对收集的数据进行中心化和白化处理。白化处理过程分别采用传统的基于协方差的PCA，基于互信息的PCA[18]以及本文提出的基于加权相关系数的PCA。得到3种不同方法下变量的特征值分布分别如图2~图4所示，其中横坐标表示某个属性，如4.1节描述，1表示%user，2表示%system，共计17个属性，纵坐标表示此属性的特征值。

以上3种方法处理后得到的主成分贡献率和累积贡献率如表3所示。可见，基于加权限关系数的PCA的主成分1的贡献率要明显高于其他2种方法，前2维的贡献率分别为92.65%，39.88%，96.61%，因此，维数相同的情况下，基于加权相关系数的PCA贡献率更大。若以贡献率95%为限选取主成分，则前2种方法分别需要3维、12维，而基于加权相关系数的PCA仅需要2维。

表2 特征属性集

表3 3种方法得到的主成分贡献率及累积贡献率

综上所述，利用基于加权相关系数的PCA进行白化处理可以在不提高维度的情况下减少信息损失，对入侵检测正确率的影响更小。若限定信息保留率，则可以保证更低的维度，减小问题规模，可以提高入侵检测的效率。

4.2.2 改进的FastICA方法性能

经过白化处理后，得到2维数据，则需提取2个独立成分。分别采用传统FastICA算法和改进FastICA算法进行独立成分提取，每组分别进行5次实验，取平均值，如表4所示。可以看到，传统FastICA在提取第一维独立成分时平均迭代次数高达51次，而改进FastICA平均仅需要迭代3.2次，大大减少了迭代次数。

表4 2种方法迭代次数对比

由2.3节可知，改进FastICA迭代序列的效率指数较传统方法有所提高，这说明改进后的方法运行效率更高，2种方法运行时间对比情况如表5所示。改进后的方法平均运行时间减少了0.25 s，从而有效提高了入侵检测的效率。

表5 2种方法运行时间对比

2种方法得到的独立成分比较如图5所示，其中横坐标表示样本数量，纵坐标表示对应独立成分的值，FastICA(1)及改进FastICA(1)表示第一个独立成分。由图可知，2种方法得到的独立成分差异不大，甚至有重合的区域。用欧氏距离来衡量它们的差异度，如下

其中，是传统方法得到的独立成分，是改进FastICA得到的独立成分。

2种方法提取独立成分后所有样本的差异度如图6所示，大部分样本的差异度分布在[0,0.2]区间，最大的差异度不超过2。因此，2种方法得到的独立成分差别不大，对后期的异常检测工作影响甚微。

综上所述，本文算法在不提高数据维度的同时减小了信息损失，不仅有效地减少了迭代次数，加快了收敛速度，而且得到的独立成分与原有方法得到的独立成分基本无差别。

5 结束语

入侵检测样本数据规模的大小，直接影响到检测算法的性能和检测率。为了更好地对样本数据进行优化，提出了一种改进的FastICA算法，引入基于加权相关系数的PCA用于白化处理过程，并提出一种三阶收敛的牛顿迭代法用于独立成分提取。通过对CPU使用情况、进程创建等计算机主要性能指标进行收集和测试，实验表明，与改进前及其他相关算法相比，本文算法不仅有效减小了白化处理过程带来的信息损失，而且减少了迭代次数，有效提高了收敛速度，为后续的入侵检测工作提供了更好的保障，有利于提高入侵检测的正确率和效率。

[1] 国家互联网应急中心. 2013年我国互联网网络安全态势综述[J/OL]. http://www.cert. org.cn.

National Internet Emergency Center. The overview of China’s Internet network security situation in 2013[J/OL]. http://www.cert.org.cn.

[2] ANDERSO J P. Computer Security Threat Monitoring and Surveillance [P]. USA: PA 19034, 1980.4

[3] LI M. An approach to reliably identifying signs of DDOS flood attacks based on LRD traffic pattern recognition[J]. Computers & Security, 2004, 23(7):549-558.

[4] 王慧强,杜晔,庞永刚.入侵检测技术研究[J].计算机应用研究, 2003, 10(20):90-94. WANG H Q, DU Y, PANG Y G. Research in intrusion detection technology [J]. Application Research of Computers, 2003, 10(20):90-94.

[5] DEREK S, GUAN Q, FU S. An anomaly detection framework for autonomic management of compute cloud systems[C]//Computer Software and Applications Conference Workshops (COMPSACW).Seoul, c2010: 376-381.

[6] GUAN Q, ZHANG Z M, FU S. Ensemble of Bayesian predictors and decision trees for proactive failure management in cloud computing systems[J]. Journal of Communications, 2012, 7(1):52-61.

[7] 夏敏纳,龚德良,肖娟.一种面向可靠云计算的自适应故障检测方法[J].计算机应用研究, 2013, 31(2):426-430. XIA M N, GONG D L, XIAO J. An adaptive fault detection method for reliable cloud computing[J]. Application Research of Computing,2013,31(2):426-430.

[8] HUSANBIR S, LIU J G, GUAN Q. AFD: adaptive failure detection system for cloud computing infrastructures[C]//Performance Computing and Communications Conference (IPCCC). Austin, TX, c2012: 71-80.

[9] ZHU Q, TERESA T, XIE Q. Automatic fault diagnosis in cloud infrastructure[C]//Cloud Computing Technology and Science(CloudCom). Bristol, c2013: 467-474.

[10] GUAN Q, FU S. Adaptive anomaly identification by exploring metric subspace in cloud computing infrastructures[C]//Reliable Distributed Systems (SRDS). Braga, c2013: 205- 214.

[11] 李娜,赵慧洁,贾国瑞.因子分析模型的高光谱数据降维方法[J].中国图象图形学报,2011, 16(11):2030-2035. LI N, ZHAO H J, JIA G R. Hyperspectral data dimensionality reduction method based factor analysis model[J]. Journal Image and Graphics,2011, 16(11):2030-2035.

[12] 李乐,章毓晋.非负矩阵分解算法综述[J].电子学报,2008, (4):737-743. LI L, ZHANG Y J. Summary of non-negative matrix factorization algorithm [J].Chinese Journal of Electronics,2008, (4): 737-743.

[13] 蓝荣祎,孙怀江.基于逆运动学和重构式ICA 的人体运动风格分析与合成[J].自动化学报,2014,40(6):1135-1147. LAN R W, SUN H J. The style analysis and synthesis of human motion based on inverse kinematics and reconstruction type of ICA [J]. Acta Automatica Sinica,2014,40(6):1135-1147.

[14] 荣宏,王会梅,鲜明.基于快速独立成分分析的RoQ攻击检测方法[J].电子与信息学报,2013,35(10):2307-2313.

RONG H, WANG H M, XIAN M. A method of RoQ attack detection based on FastICA [J]. Journal of Electronics & Information Technology,2013,35(10):2307-2313.

[15] 吴逊.基于独立成分分析的特征提取方法研究[D]. 厦门：厦门大学，2007. WU X. The Research on Features Extraction Method Based on Independent Component Analysis [D]. Xiamen: Xiamen University, 2007.

[16] 张卷美.一种新的迭代收敛阶数的证明与推广[J].大学数学，2007,23(6):135-139. ZHANG J M. A new proof and promotion of iteration convergence order [J]. College Mathematics,2007,23(6):135-139.

[17] 于明明,张妍.牛顿迭代法与几种改进格式的效率指数[J].数学的实践与认识,2008,38(18):154-159. YU M M, ZHANG Y. The efficiency index of Newton iterative method and serveral improve formats[J]. Journal of Mathematics in Practice and Theory,2008,38(18):154-159.

[18] 范雪莉,冯海泓,原猛.基于互信息的主成分分析特征选择算法[J].控制与决策，2013,28(6):915-919. FAN X L, FENG H H, YUAN M. Principal components analysis based on mutual information for feature selection algorithm [J]. Control and Decision, 2013,28(6):915-919.

Improved FastICA algorithm for data optimization processing in intrusion detection

DU Ye, ZHANG Ya-dan, LI Mei-hong, ZHANG Da-wei

(School of Computer and Information Technology, Beijing Jiaotong University, Beijing 100044, China)

For the purpose of achieving the better data optimization processing results in intrusion detection, an improved FastICA algorithm was proposed. The weighted correlation coefficient was adopted in the phase of albinism processing to reduce information loss, and the Newton’s iterative method was improved for third-order convergence. The algorithm was introduced concretely, meanwhile the time complexity was analyzed in detail. The experiment shows that the method has the advantages of less times of iteration and fast speed of convergence, which can effectively decrease the losses of data and increase the efficiency of data optimization in intrusion detection.

intrusion detection, fast independent component analysis, data optimization, Newton’s iteration method

TP393

A

10.11959/j.issn.1000-436x.2016006

2014-12-23；

2015-03-11

北京高校青年英才计划基金资助项目（No.YETP0548）；中央高校基本科研业务费基金资助项目（No.2014JBM030）；国家自然科学基金资助项目（No.61102105）

Beijing Higher Education Young Elite Teacher Project (No.YETP0548), The Fundamental Research Funds for the Central Universities (No.2014JBM030), The National Natural Science Foundation of China (No.61102105)

杜晔（1978-），男，黑龙江哈尔滨人，博士，北京交通大学副教授，主要研究方向为网络安全、形式化验证与可靠性分析。

张亚丹（1989-），女，河北石家庄人，北京交通大学硕士生，主要研究方向为入侵检测与响应、安全态势感知。

黎妹红（1975-），男，湖北黄梅人，博士，北京交通大学讲师，主要研究方向为智能卡与生物识别技术、信息保密技术。

张大伟（1974-），男，辽宁沈阳人，博士，北京交通大学讲师，主要研究方向为可信计算、智能卡安全技术。