音速喷嘴内水蒸气自发凝结流动自激振荡和分歧现象

王 超，王 刚，丁红兵



音速喷嘴内水蒸气自发凝结流动自激振荡和分歧现象

王 超1, 2，王 刚1, 2，丁红兵1, 2

(1. 天津大学电气与自动化工程学院，天津 300072；2. 天津市过程检测与控制重点实验室，天津 300072)

气体在喷嘴中流动伴有很大的温降，会使其中的水蒸气发生凝结，并对其计量产生影响．针对音速喷嘴中过热水蒸气自发凝结流动产生的非稳态自激振荡和流动分歧现象，建立了考虑黏性的水蒸气自发凝结数值模型；根据凝结诱导的气动激波的振荡幅度将自激振荡分为3种不同的模式，其中模式Ⅲ的压力波动会波及喉部上方，且会出现非对称流动分歧现象，而模式Ⅰ中气动激波仅在平衡位置附近小幅度振荡；最后研究了自激振荡对喷嘴的质量流量的影响，并给出了相应的修正系数，最小值为0.988，需要加以重视．

音速喷嘴；自发凝结流动；自激振荡模式；流动分歧；质量流量

音速喷嘴具有性能稳定、准确度等级高等特点，因此作为一种流量测量和传递的标准受到了广泛的关注和使用[1]．但是，由于其流量受喷嘴结构尺度、加工精度、压力和湿度等多种因素的影响，目前仍存在很多尚未解决或待确定的问题．特别是由于喷嘴的测量对象多含有水蒸气，而气体在音速喷嘴内高速流动而产生的温度骤降会使水蒸气发生凝结现象，研究其变化规律以及对喷嘴流量计量精度的影响具有重要的意义．

早在1973年，德国的Aschenbrenner等[2]首次针对喷嘴内含湿气体的流动进行了探索性研究，并提出了不考虑凝结的混合气体湿度修正公式．此后，李春辉等[3]、Stewart等[4]均从混合气体热力学关系式角度获得了湿度修正公式，但是并没有形成统一修正标准．韩国的Lim等[5]及澳大利亚的Chahine等[6]分别于2011年和2013年发现实际流量均大幅低于各国的湿度修正公式，极有可能是因为水蒸气“凝结”现象造成，认为需要对音速喷嘴内凝结现象加以重视并进行细致的研究．

自发凝结一般不会在喷嘴喉部之前发生[7-8]．但即便凝结发生在喉部之后的扩散段，凝结也可能对喉部前流场产生影响，并最终影响到喷嘴的流量及其准确计量．Pouring[9]和Skilling[10]均各自从实验角度观测到流动的“非稳态”自激振荡现象，频率范围从数百赫兹至上万赫兹，规律复杂多变．Adam等[11]从实验角度研究了非稳态振荡现象，将其分为不同的振荡模式，并详细分析了不同模式下振荡规律．随着计算机技术的发展，更多学者通过CFD手段研究凝结自激振荡现象．李亮[12]、Ma等[13]、Wróblewski等[14]和Dykas等[15]建立了二维及三维CFD数值模型，用于模拟蒸汽自发凝结流动并观察自激振荡现象．

另外，自激振荡的流动分歧即非对称现象的发现使得凝结现象对喷嘴流量的影响更为复杂难解．Adam等[11]于1997年在超音速风洞实验中观测到由湿空气非稳态凝结引起的流动分歧现象，并通过简单非稳态数值模拟加以验证；随后Simpson等[16]在蒸汽自发凝结过程中也观测到流动分歧现象，并且用非黏性二维模型进行了数值模拟，但只在一种结构一种边界条件下出现了分歧现象；武汉大学Yu等[17]在2015年对前人的工作进行了深入研究，发现对于不同结构的喷嘴，分歧现象出现的条件不同．

但是，以上研究并没有关注凝结自激振荡现象对音速喷嘴流量的影响，且仿真模型大多未考虑流体的黏性，不能真实反映流场状态．为更加系统地研究凝结产生的自激振荡现象，本文建立考虑黏性的欧拉-欧拉坐标系下的水蒸气自发凝结模型，研究自激振荡频率和流量变化与入口过冷度的关系，分析凝结“非稳态”不同振荡模式对流场、流量和流量稳定性造成的影响．

1 喷嘴流动

1.1 计量原理

音速喷嘴主要用于计量单相气体质量流量，其常用结构如图1所示．其中为音速喷嘴入口滞止压力，为出口压力，则为节流压力比[18]，也称背压比．

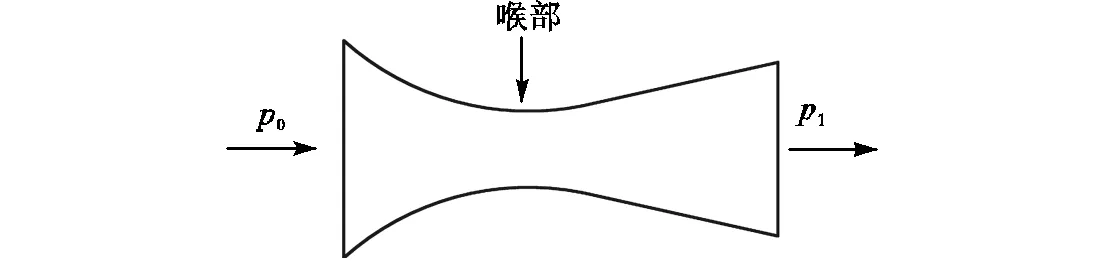
图1 音速喷嘴结构

根据气体动力学原理，存在一个使喉部气体速度最大的背压比，称为临界背压比．当满足临界条件时气体在喉部的速度达到当地音速．若0不变，减小1，流速不再变化，此时流过喷嘴的质量流量[18]为

   (1)

式中：q为质量流量，kg/s；为喉部内截面积，m2；C为流出系数；为临界流函数；0为滞止温度，K；为通用气体常数，约为8.314,41,J/(mol·K)；为气体摩尔质量，kg/mol．

流出系数C是表征音速喷嘴流量特性的重要指标，定义[18]为

   (2)

式中：q,i为相同滞止条件下，气体一维等熵地流过喷嘴的理想质量流量．

当介质不含有可凝气体时，其质量流量q可由上述单相流计算式获得．然而，当介质中含有可凝气体时，需要考虑凝结对入口流量带来的影响，降低其计量精度．以本文研究对象干蒸汽为例，此时喷嘴入口的干蒸汽质量流量为hom．根据定义，凝结引起的入口质量流量变化可由修正系数hom表示，具体形式为

   (3)

1.2 水蒸气自发凝结过程

一般认为蒸汽或者含湿气体在越过饱和线后就会发生凝结，但是当其十分纯净，又没有壁面帮助其在上面发生凝结时，气体在越过饱和线后需要达到一个极限值才能开始发生凝结，这个极限值叫做Wilson点，如图2所示，从不同的滞止点出发可以达到不同的Wilson点，这些点可以连成一条曲线，叫做Wilson线[7]，基本与饱和线平行．对于喷嘴内部的湿蒸汽流动，气体沿着喷嘴膨胀加速，温度和压力逐渐降低，一般在喉部下游某个截面处达到饱和，但凝结不会发生，而是会继续膨胀至过冷区，只有当气体达到Wilson点后凝结核才会突然出现，膨胀过程如图3所示．

在对水蒸气自发非稳态凝结过程进行数值模拟之前，需要从气体动力学角度对该现象进行分析．水蒸气凝结时会释放大量的相变潜热，使得超音速气流向音速点靠近．在不同入口条件下，凝结发生的位置和强度均不同，释放的凝结潜热也不同．对于一定马赫数的流动，存在一个临界加热量c使气体速度由超音速减为音速．因此，凝结放热量与临界加热量c的关系不同，导致自发凝结流动状态也不同[12].

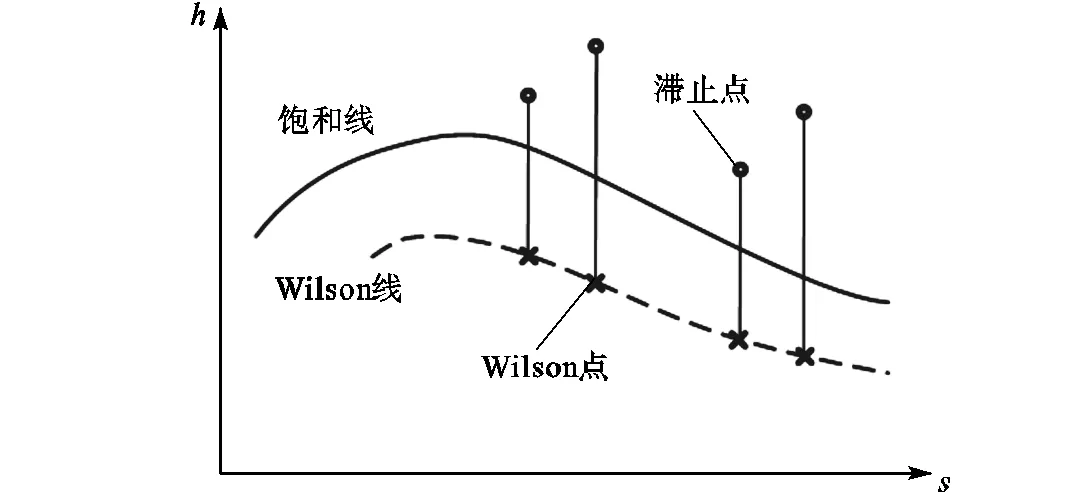
图2 焓熵(h-s)图中的Wilson线

图3 音速喷嘴中湿蒸气膨胀凝结过程

(1) 当＜c时，不足以使气流减速到亚音速，凝结的影响只是使得压力出现突跃，出现“凝结突跃”，流动仍然是稳定的；从控制方程的角度来讲，此时动量方程的微分形式存在实数解[19]．

(2) 当≥c时，出现气动激波，但流动仍然是稳定的，也就是说，此时动量方程需要引入激波才能得到实数解．

可见，自激振荡现象是由凝结过程放热和超音速气流相互作用造成的，这种不稳定的流动状态势必会对喷嘴流量造成影响，当分歧现象导致的流动不对称状态出现时，这种影响将更加复杂多变，针对此问题，本文展开了一系列数值研究与理论分析．

2 数学模型与数值方案

2.1 凝结模型

数值计算采用基于欧拉-欧拉坐标系的Navier-Stokes黏性流动凝结模型，其中蒸汽为连续相，以下标“c”表示，小液滴以均相凝结的形式出现，作为离散相，以下标“d”表示，并且不存在相间滑移，即离散相与连续相以相同的速度移动．

连续相使用SST湍流模型对雷诺平均N-S方程进行求解．其质量守恒方程张量形式为

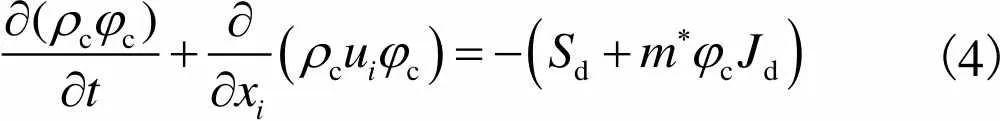
   (4)

式中：c为连续相密度；c为连续相体积分数；u为方向的速度分量；d为液滴总生长率；d为成核率，即单位时间内单位体积的蒸汽生成的液滴数；*为基于临界半径*的成核液滴质量．

连续相动量守恒方程的张量形式为

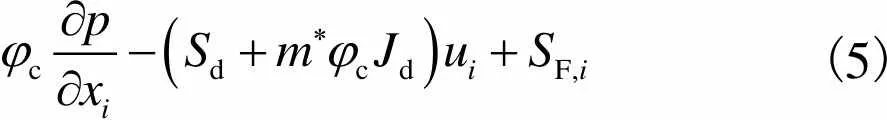
     (5)

其中源相F,i包含雷诺应力张量的最小项，对于可压缩流体，有

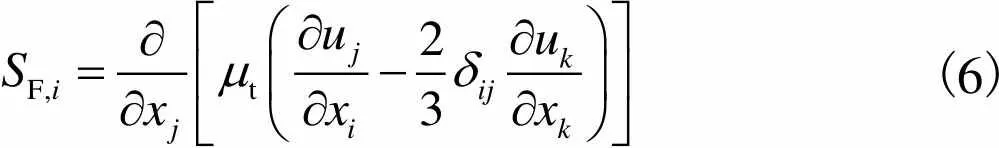
   (6)

另外，将连续相能量方程以总焓c的形式给出，即

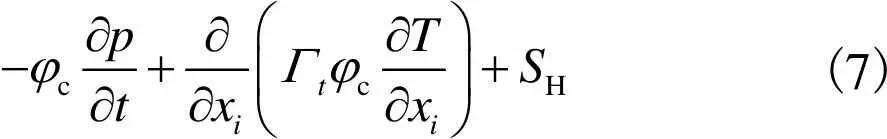
     (7)

其中总焓定义为

   (8)

式中：c为蒸汽静态焓；为湍流动能．源相H包含相间的热交换．

对于离散相，质量守恒方程为

   (9)

其中，离散相体积分数d和连续相体积分数c的约束条件为

   (10)

离散相的能量方程形式与连续相类似．

   (11)

液滴开始成核时的临界半径为

   (12)

式中：∆c为气相Gibbs自由能的变化量，由状态方程决定；为液滴表面张力，可以通过体积表面张力乘以体表面张力系数(取0.94)得到．

根据液滴经典成核理论，成核率公式为

   (13)

式中：c为成核率修正系数；为玻耳兹曼常数；为一个水分子的质量；为Kantrowitz非等温校正因子，且有

   (14)

fc为平衡潜热；为水蒸气的比热比和气体常数．

液滴半径的变化率为液滴生长率，定义为

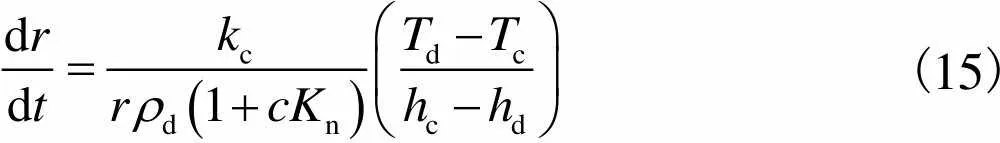
   (15)

式中为经验系数[20]．液滴温度d定义为

   (16)

式中：s()为蒸汽压力对应的饱和温度；∆为气相过冷度；为液滴半径．

2.2 水和水蒸气模型

本文利用IAPWS-IF97(International Association of Properties of Water and Steam-Industrial Formulation 1997)水和水蒸气热力性质模型对介质进行定义．

IAPWS-IF97公式的适用范围[21]为

整个适用范围被划分为5个小分区，每个分区使用不同的模型公式，如图4所示．在分区1和分区2中分别使用比Gibbs自由能函数(，)；分区3使用比Helmholtz自由能函数(，)；饱和线由饱和压力方程s()定义；同时，高温分区5也使用比Gibbs自由能函数．这5个函数共同组成了IAPWS-IF97的“基本方程”[21]．

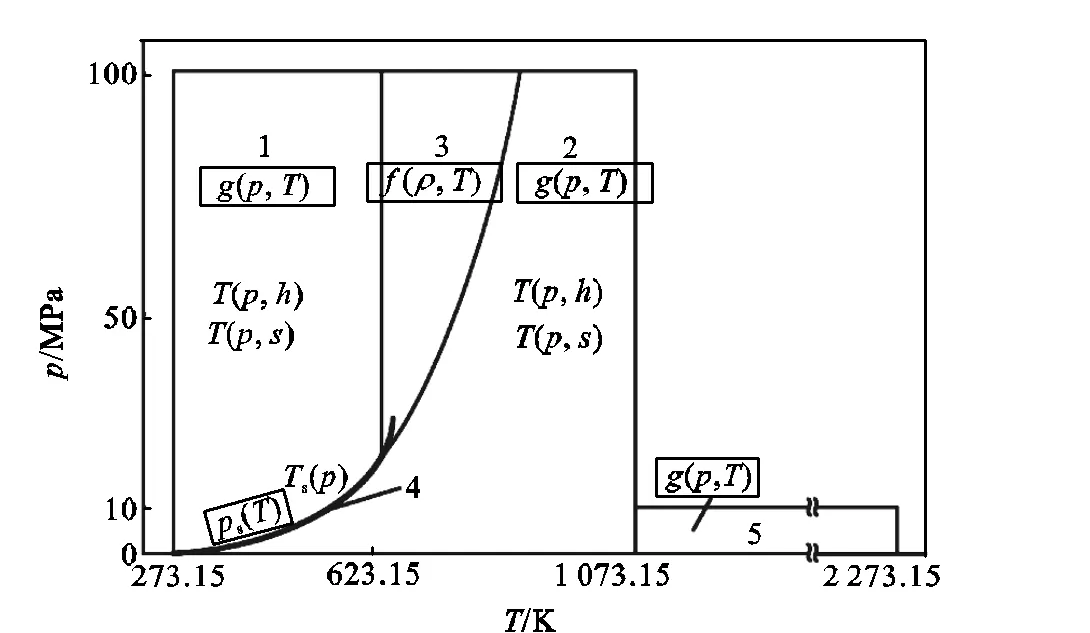
图4 IAPWS-IF97各区域划分及公式

除基本方程外，分区1、分区2和分区4有如图4所示的“后向方程”．对于分区1和分区2其形式为(，)和(，)，在分区4内其形式为s()．方程的具体形式由于篇幅限制不便展开．这些后向方程在数值上与相应的基本方程一致，并可以使方程的计算速度大大提高．

2.3 数值方案

采用四边形结构化网格以及基于有限元的有限体积法全隐式求解器，对上述模型进行数值计算．对流项离散方法采用高分辨率差分格式，输运项离散方法采用二阶后向欧拉格式，湍流项的离散格式采用一阶迎风格式．入口和出口分别设定为亚音速总压入口和超音速出口，导热分别采用第1类和第2类边界条件．流体模型使用SST湍流模型，介质使用IAPWS-IF97模型进行定义．收敛的判定基于计算域内所有控制体积的平均残差．

3 稳态凝结仿真结果与实验对比

利用Moore等[22]所做的编号为B的喷嘴实验数据来验证上述数学模型和数值方案的准确性．当喷嘴入口压力0＝25,kPa、滞止温度0＝357.6,K时，喷嘴中心场稳态压力分布仿真结果与实验对比如图5所示，同时给出不考虑凝结作用时的压力分布计算结果作为参照，如图5中虚线所示．

从图5可以看到，仿真结果与实验数据基本一致，说明本文所述数学模型，包括汽相控制方程(4)、(5)和(7)以及液相控制方程(9)和(11)等，能够有效预测喷嘴内水蒸气自发凝结过程．

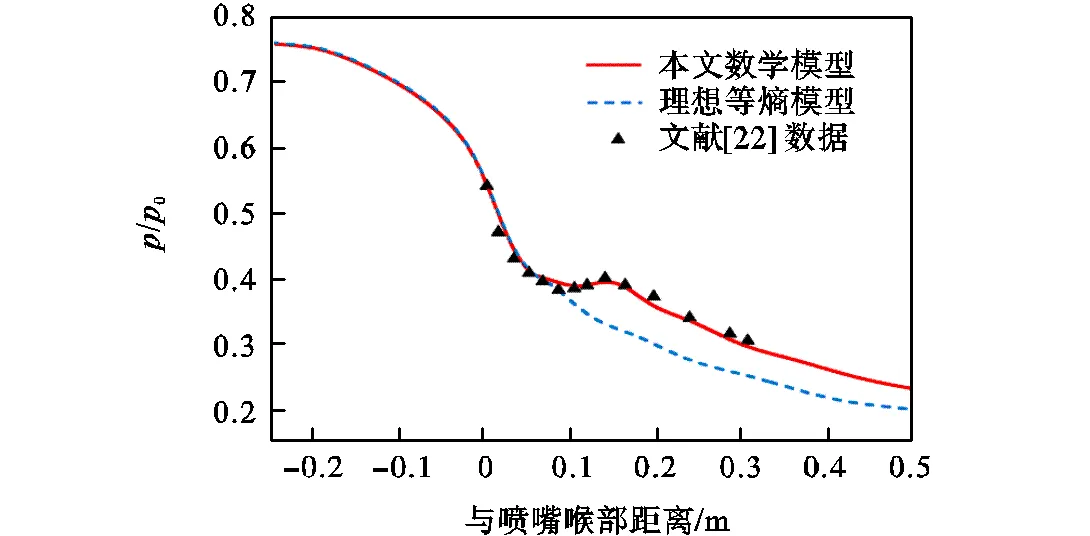
图5 稳态仿真结果与文献[22]实验数据对比

4 非稳态凝结仿真结果及分析

非稳态研究采用Moore等[22]所做实验中的E喷嘴，如图6所示，其喉部直径＝140,mm．2D结构化网格经独立性测试后确定网格数为900×120．时间步长为10-5,s，总迭代时间为1,s，残差值为10-5．边界条件方面，入口气体为干蒸汽，总压为0.1,MPa，对应饱和温度为372.78,K，保持入口为过热状态，改变入口总温，得到不同的凝结自激振荡模式．

图6 E喷嘴物理结构及尺寸

4.1 自激振荡流动模式

定义入口过冷度∆0为入口压力0对应的饱和温度s(0)和入口总温0的差值，即∆0＝s(0)－0．则在本研究中，有s(0)＝372.78,K．

图7所示分别为∆0＝－11.22,K、－10.22,K和－3.22,K时一个周期内喷嘴中心场压力分布．可以看到，在不同入口过冷度下，均出现了气动激波的周期性振荡情况，只是振荡的幅度不同．则根据图7中气动激波的振荡幅度，并结合气体动力学原理，可以将喷嘴内自发凝结引发的自激振荡流动现象分为3种模式.

(1)模式Ⅰ：如图7(a)所示，单一激波在平衡位置附近小幅振荡，伴有凝结强弱的交替变化．

(2)模式Ⅱ：如图7(b)所示，随着激波波动幅度的增大，激波向上游移动，促使成核区上游的气温升高，凝结强度减弱，气动激波强度慢慢衰减直至消失，从而使凝结再次增强，新的气动激波产生，并继续向上游移动，周而复始形成一个循环振荡周期．

(3)模式Ⅲ：如图7(c)所示，激波会一直运行至喉部上游再逐渐衰弱为压缩波，此时，扰动可以传播至喷嘴入口，进而影响整个流场．

图8为0＝0.1,MPa时，喷嘴喉部中心后方70,mm(0.5)处的压力振荡频率和幅值与入口过冷度∆0的关系．根据图8所示压力振荡频率和幅值与∆0的关系，可以得到上述自激振荡模式的气动激波运动规律．在振荡模式Ⅰ和Ⅱ下，随着∆0的增大，激波波动的幅度变大，而波动频率变小；而在振荡模式Ⅲ下，∆0越大，压力波动幅度先继续增大再减小，而对于波动频率，由于∆0增大后凝结区更接近喉部，因此，波动频率会随着∆0增大而增大．

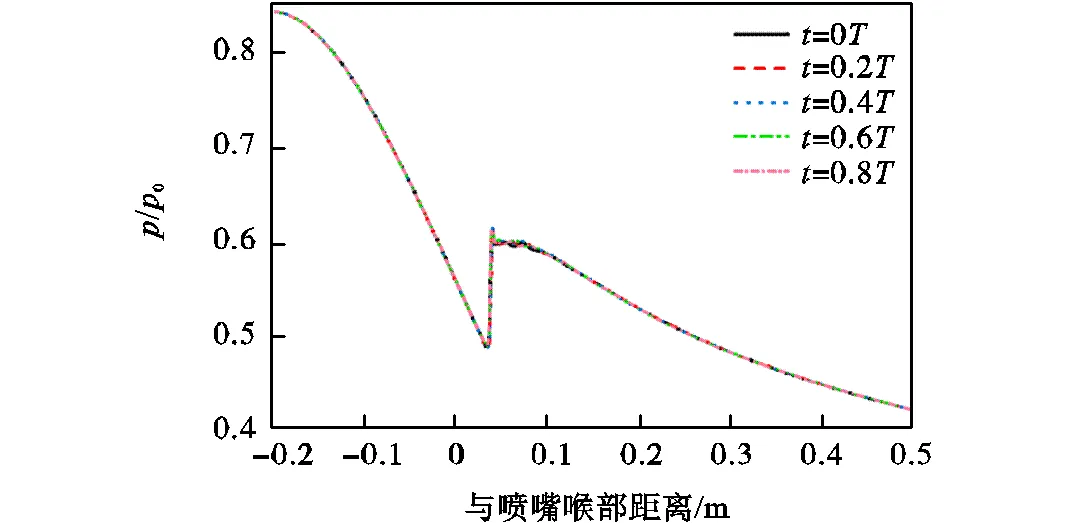
（a）∆0＝-11.22,K(振荡模式Ⅰ)

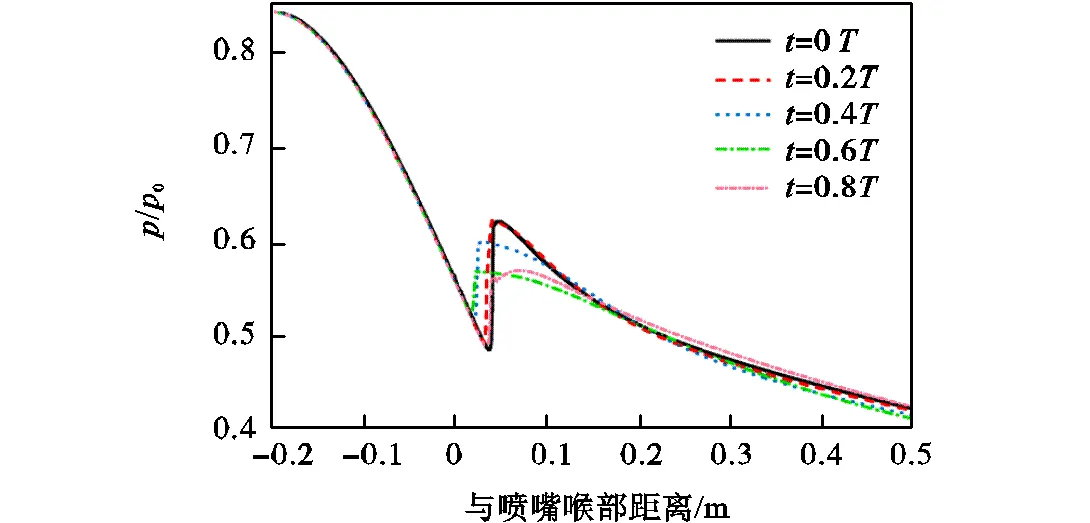
（b）∆0＝-10.22,K(振荡模式Ⅱ)

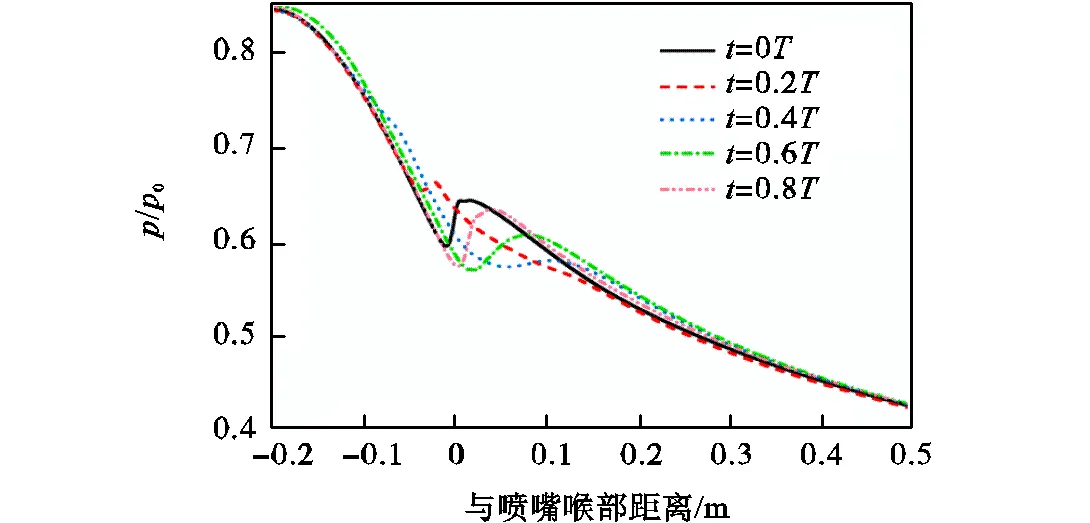
（c）∆0＝-3.22,K(振荡模式Ⅲ)

图7 周期内中心场轴向压力分布

Fig.7 Nozzle central line pressure distribution for one period of oscillation

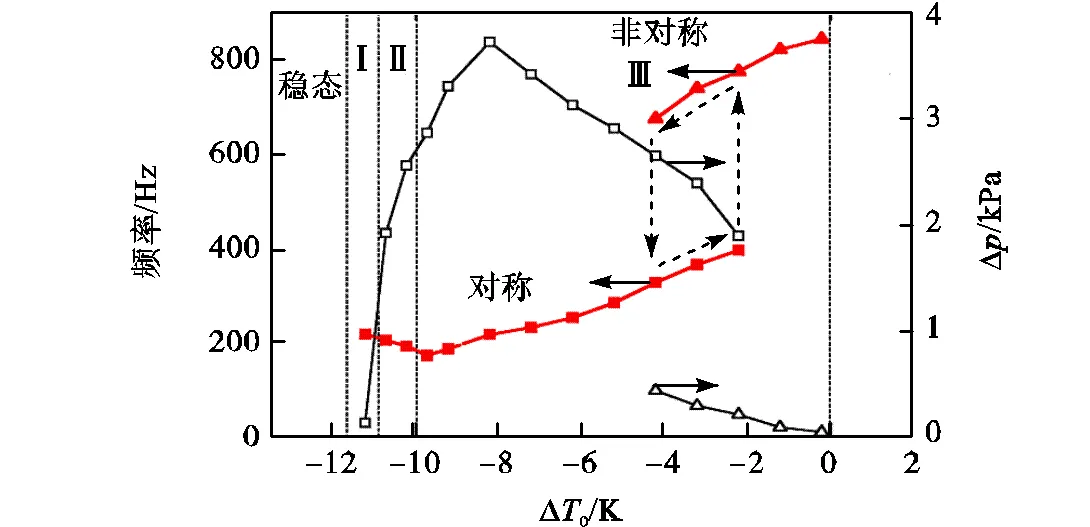
图8 不同自激振荡模式下频率f和幅值Dp

4.2 流动分歧现象

如图8所示，在模式Ⅲ中，当∆0增大到一个临界值(∆0＝－2.22,K)时，喷嘴内产生了流动分歧现象，即自激振荡频率突变为原来的2倍，而振荡幅度减小．观察喷嘴内的流动状态可以看到，流场从以轴线对称的流动模式(图9(a))过渡为非对称的模式(图9(b))．

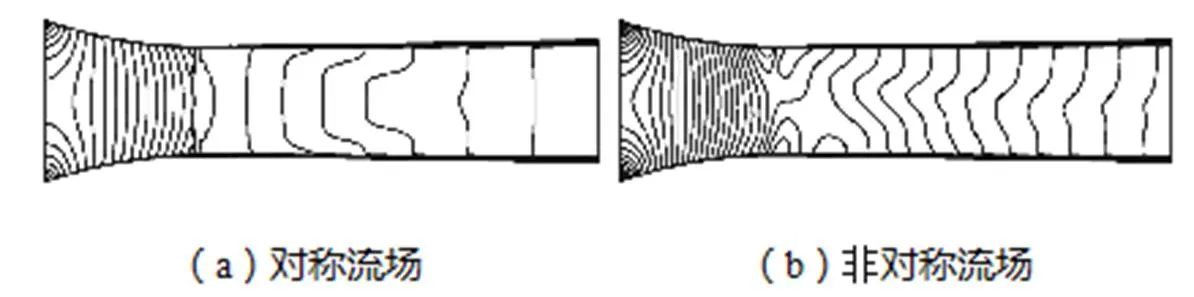
图9 对称和非对称模式下的等马赫数线图

图10为该过渡过程中喷嘴喉部处壁面压力波动曲线．在非对称流动出现之前，流场的自激振荡保持初场状态，若干个振荡周期之后，频率提高到原频率的近2倍，开始出现非对称的自激振荡现象．此时，若继续增大∆0，流场将逐渐转变为稳态，自激振荡的影响逐渐消除；若减小∆0，流场将继续保持非对称状态，直到另一临界值(∆0＝－4.22,K)，流场将再次转为对称状态，非对称与对称的频率特性曲线形成了一个“迟滞环”，如图8中带虚线箭头所示．

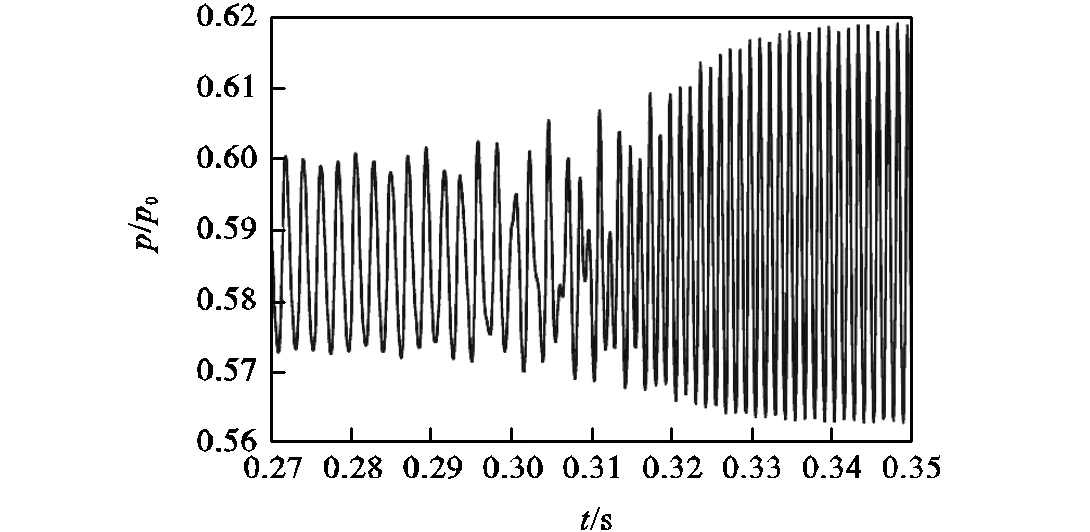
图10 对称模式到非对称模式的过渡过程

当∆0＝-3.22,K时，单个周期内非对称流动模式的∂/∂和lg如图11所示．其中∂/∂相当于喷嘴流场纹影图，可以用来表现气动激波的状态；为液相成核率，lg可呈现出不同的相变情况．可以看到，非对称模式是由凝结诱导的斜激波造成的，在一个周期内，斜激波状态不断变化，并对水蒸气相变过程产生影响．

从气体动力学角度分析，流动分歧现象产生的原因主要是流场中存在以下不稳定因素．

(1)本文所研究的喷嘴E具有大曲率收缩段以及低膨胀率的扩张段，当入口过冷度较高时，凝结区靠近喉部，膨胀率的不均匀分布使壁面附近凝结进程强度大于轴线附近，导致凝结区在轴线两侧都存在较强的法向梯度．

图11 单周期非对称模式∂r/∂x和lg J云图

(2)壁面附近和轴线附近的凝结区之间存在较复杂的耦合作用．

(3)数值模拟中还发现，在分歧段，壁面附近成核区加热的对象是速度接近音速的亚音速汽流，而汽流在一定马赫数范围内被加热温度会降低，此时凝结进程反而会增强，即凝结区附近的温度变化存在两个拐点．

可以知道，以上不稳定因素使流场处于一种亚稳定状态，如果此时呈对称振荡的流场受到较大的扰动，如提高入口过冷度，则只能得到非对称振荡的流场．这样对称和非对称流场在一定条件下就会互相转换，形成了流动分歧现象．

4.3 自激振荡对流量的影响

当凝结引起的气动激波到达喷嘴喉部时，必然引起入口干蒸汽质量流量的波动．同时仿真结果表明，自激振荡现象仅在模式Ⅲ对喷嘴流量造成较大影响．因此主要关注模式Ⅲ下对称和非对称流动的入口质量流量波动．

图12为D0＝－3.22,K时，对称和非对称模式下质量流量波动的对比情况，图中纵坐标为凝结修正系数hom，通过式(3)进行计算．可以看到，自激振荡现象使喷嘴的流量小于稳态值，并且对称流动的质量流量在数值上波动更大，而非对称流动的质量流量仅在小范围内波动或者保持恒定，可以猜想，这是由于流动的非对称性使喉部截面压力处于动态平衡的状态.

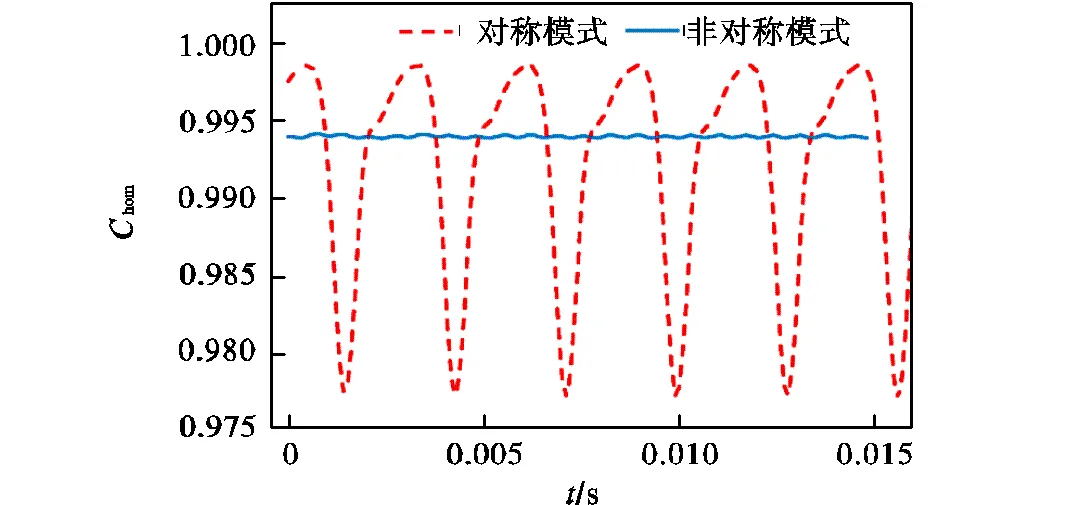
图12DT0＝-3.22,K对称和非对称模式下质量流量波动

Fig.12 Mass flow rate fluctuations of symmetric mode to asymmetric mode whenDT0＝-3.22,K

   (17)

结合式(3)可得凝结自激振荡现象对喷嘴流量影响的修正系数均值为

   (18)

则可以得到凝结对喷嘴质量流量影响的修正系数均值，如图13所示．可以看到，在相同∆0下，对称模式的自激振荡对流量造成了更大的影响．在发生分歧现象后，非对称流场的流量波动较小，但是流量平均值可以达到更大的流量偏差．本研究中自激振荡对流量影响的修正系数最小为0.988，即流量变化量最大为1.2%,，需要加以重视．

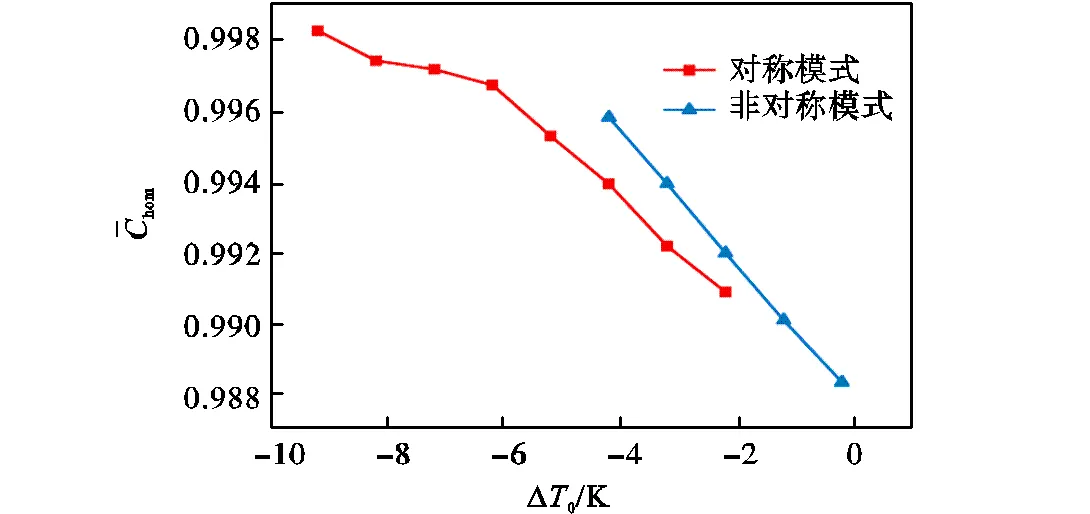
图13 凝结对音速喷嘴质量流量影响的修正系数均值

   (19)

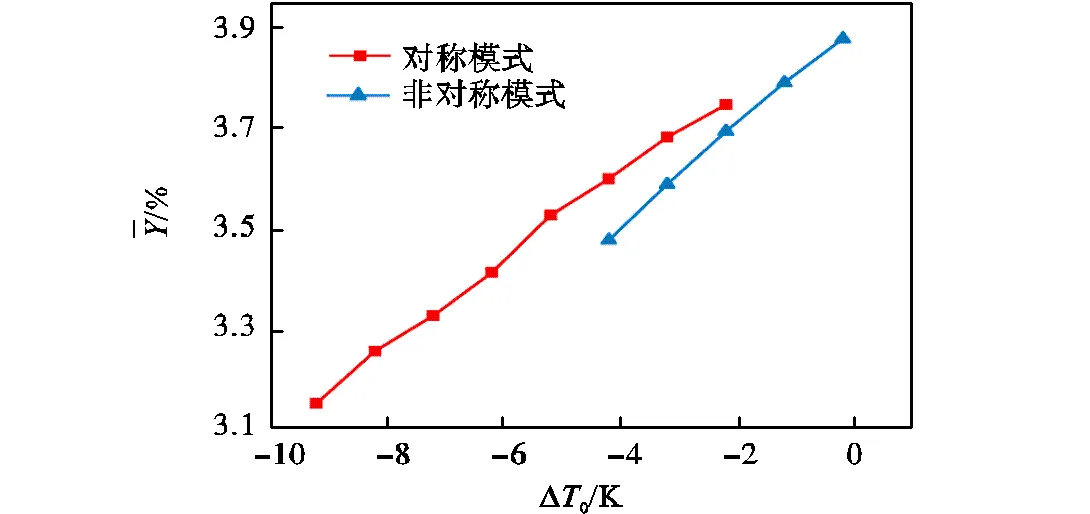
图14 音速喷嘴出口湿度与入口过冷度DT0的关系

5 结 语

本文建立了水蒸气自发凝结非稳态黏性模型，并利用实验数据验证了模型的正确性．利用该模型计算获得了当压力入口为0.1,MPa时凝结自激振荡不同的振荡模式及流动分歧现象．重点分析流动分歧现象发生规律及原因．最后，研究了上述现象对音速喷嘴质量流量的影响，结果表明，凝结引起的变化高达1.2%,，值得注意．因此，研究结果可用来评估水蒸气凝结现象影响，拓宽音速喷嘴应用范围，并提高其计量精度．

［1］ Ding H B，Wang C，Zhao Y K. Flow characteristics of hydrogen gas through a critical nozzle[J].，2014，39(8)：3947-3955.

［2］ Aschenbrenner A，Narjes L. Untersuchung des feuchteeinflusses auf den durchfluss durch düsen bei überkritischem druckverhältnis[J].，1973，84：381-385.

［3］ 李春辉，王 池. 通过音速喷嘴气体流量的湿度修正方法研究[J]. 计量学报，2007(增1)：160-164.

Li Chunhui，Wang Chi. The humidity correction on the flow through sonic nozzle[J].，2007(Suppl 1)：160-164(in Chinese).

［4］ Stewart D G，Watson J T R，Vaidya A M. The effect of using atmospheric air in critical flow nozzles[C]//4Denver，Colorado，USA. 1999.

［5］ Lim J M，Yoon B H，Oh Y K，et al. The humidity effect on air flow rates in a critical flow venturi nozzle [J].，2011，22(5)：402-405.

［6］ Chahine K，Ballico M. Evaluation of the effect of relative humidity of air on the coefficients of critical flow venturi nozzles[C]//. Paris，France，2013：24-26.

［7］ 蔡颐年，王乃宁. 湿蒸汽两相流[M]. 西安：西安交通大学出版社，1985.

Cai Yinian，Wang Naining.[M]. Xi’an：Xi’an Jiaotong University Press，1985(in Chinese).

［8］ Wyslouzil B E，Heath C H，Cheung J L，et al. Binary condensation in a supersonic nozzle[J].，2000，113(17)：7317-7329.

［9］ Pouring A. Thermal choking and condensation in nozzles [J].，1965，8(10)：1802-1810.

［10］ Skilling S A. An Analysis of the Condensation Phenomena Occurring in Wet Steam turbine[D]. Birmingham：University of Birmingham，1987.

［11］ Adam S，Schnerr G. Instabilities and bifurcation of non-equilibrium two-phase flows[J].，1997，348：1-28.

［12］ 李 亮. 存在自发凝结的湿蒸汽两相非平衡凝结流动数值研究[D]. 西安：西安交通大学能源与动力工程学院，2002.

Li Liang，Numerical Study on the Nonequilibrium Wet Steam Two-phase Flows with Spontaneous Condensation [D]. Xi’an：School of Energy and Power Engineering，Xi’an Jiaotong University，2002(in Chinese).

［13］ Ma Q F，Hu D P，Jiang J Z，et al. A turbulent Eulerian multi-fluid model for homogeneous nucleation of water vapour in transonic flow[J].，2009，23(3)：221-231.

［14］ Wróblewski W，Dykas S，Gepert A. Steam condensing flow modeling in turbine channels[J].，2009，35(6)：498-506.

［15］ Dykas S，Wróblewski W. Numerical modelling of steam condensing flow in low and high-pressure nozzles[J].，2012，55(21/22)：6191-6199.

［16］ Simpson D A，White A J. Viscous and unsteady flow calculations of condensing steam in nozzles[J].，2005，26(1)：71-79.

［17］ Yu X G，Xie D，Wang C，et al. Numerical investigation of oscillating flows with nonequilibrium condensation in nozzles[J].，2015，31(3)：837-842.

［18］ 林建忠．流体力学[M]. 北京：清华大学出版社，2013.

Lin Jianzhong．[M]. Beijing：Tsing- hua University Press，2013(in Chinese)．

［19］ Delale C F，Lamanna G，van Dongen M E H. On the stability of stationary shock waves in nozzle flows with homogeneous condensation[J].，2001，13(9)：2706-2719.

［20］ Gerber A G，Kermani M J. A pressure based Eulerian-Eulerian multi-phase model for non-equilibrium condensation in transonic steam flow[J].，2004，47(10)：2217-2231.

［21］ Wagner W，Cooper J R，Dittmann A，et al. The IAPWS industrial formulation 1997 for the thermodynamic properties of water and steam[J].，2000，122(1)：150-184.

［22］ Moore M J，Walters P T，Crane R I，et al. Predicting the fog-drop size in wet-steam turbines[J].，1974，C37/73：101-109.

(责任编辑：孙立华)

Spontaneous Condensation Steam Flow with Self-Excited Oscillation and Bifurcation Phenomenon in Sonic Nozzles

Wang Chao1, 2，Wang Gang1, 2，Ding Hongbing1, 2

(1. School of Electrical Engineering and Automation，Tianjin University，Tianjin 300072，China；2. Tianjin Key Laboratory of Process Measurement and Control，Tianjin 300072，China)

The gas temperature will drop greatly when the gas flows through the nozzle，which leads to the condensation of the vapor．To investigate the phenomenon of self-excited oscillation and bifurcation induced by spontaneous condensation of the pure superheated steam flow，a numerical viscous model of supersonic nozzle flow was established．Three self-excited periodic oscillation modes were classified according to the oscillation amplitude of aerodynamic shock．It is found that the pressure fluctuations spread to the upstream of the nozzle throat in mode Ⅲ，while the shock in modeⅠoscillates with small amplitude．Moreover，the effect of self-excited oscillation on the mass flow rate of nozzle was studied in detail．Correction factor for condensation effect was obtained and the minimum value was 0.988，which calls for pay more attention.

sonicnozzles；spontaneous condensation of flow；self-excited oscillation mode；bifurcation of flow；mass flow rate

10.11784/tdxbz201604052

TH814

A

0493-2137(2016)11-1113-08

2016-04-20；

2016-07-19.

国家青年科学基金资助项目(51506148)；天津市自然科学基金资助项目(15JCYBJC19200，16JCQNJC03700).

王 超（1973—  ），男，博士，教授，wangchao@tju.edu.cn.

丁红兵，hbding@tju.edu.cn.