三相单芯电力电缆芯线等效阻抗和导纳参数计算方法

李博通，张云柯



三相单芯电力电缆芯线等效阻抗和导纳参数计算方法

李博通，张云柯

(天津大学智能电网教育部重点实验室，天津 300072)

含三相单芯电力电缆的高压交流系统继电保护整定及短路电流计算需要获得精确的电缆芯线等效阻抗和导纳参数. 首先对考虑各导体层间互感和电容影响的三相单芯电力电缆阻抗及导纳矩阵特征进行了分析，针对电缆外导体层的不同接地方式给出了外导体层中电压电流的边界条件，在此基础上研究了导体层互感和电容的消去方法，提出了三相单芯高压电力电缆芯线等效阻抗和导纳的计算方法. 针对三相单芯电缆的一点接地、两端接地、交叉互联接地3种常用接地方式搭建了PSCAD模型，并通过仿真验证了本算法的准确性.

单芯电力电缆；芯线；接地方式；阻抗矩阵；导纳矩阵

高压电力电缆在跨江海输电及城市负荷中心供电等方面获得了广泛的应用．为进行电力系统短路电流计算、保护整定等工作，需要获得精确的电缆阻抗和导纳参数，但是，高压电力电缆为多层结构，各导体层之间的电磁及电容耦合使得电缆参数计算比架空线要复杂得多．因此，实际应用中一般采用电能传输载体即芯线的参数进行电力系统分析和计算，以尽量避免多维的复杂矩阵运算，提高运算速度，降低计算误差．如何计及导体层参数的相互影响，进行电缆芯线等效阻抗和导纳的准确计算，是含电缆的电力系统分析和计算的基础．

电缆参数的复杂性已经被业内众多专家学者所重视并开展了针对性研究．文献[1]对同轴导体电磁特性进行了详细分析和理论推导，是电力电缆参数计算的理论基础．文献[2]给出了考虑屏蔽层和铠装层的同轴电缆的阻抗和导纳计算公式．文献[3]考虑了电缆参数的频率相关特性，给出了电缆电磁暂态仿真建模方法．文献[4]建立了电缆阻抗矩阵和导纳矩阵，并对电缆行波传输过程进行了分析．文献[5]阐述了金属屏蔽层不同的接地互联方式下电缆相序阻抗参数特点和各序阻抗之间的关系．文献[6]研究了高压和超高压电力电缆线路参数的现场测试方法，提出能够快速准确测量电力电缆正序和零序阻抗的现场测试技术．文献[7]对交叉互联电缆线路的参数进行了实际测量，分析了金属屏蔽层不同的接地方式对零序阻抗及互感阻抗产生影响的原因．

上述文献重点分析了电缆阻抗及导纳的计算方法，部分文献给出了考虑各导体层间耦合的电缆阻抗矩阵，但均未涉及对考虑电缆多导体层间耦合的芯线等效参数计算方法的研究．本文在分析电缆外导体层接地方式的基础上，研究计及外导体层影响的电缆芯线等效阻抗及导纳计算方法，并对方法的准确性进行了仿真验证．

1 电缆传输方程

35,kV及以上高压电力电缆一般采用同轴结构的三相单芯电缆，其芯线为电能传输载体，芯线外为多绝缘层与导体层的混合结构．目前已广泛应用的6层结构交联聚乙烯XLPE单芯电缆结构如图1所示，除芯线为导体层外，还包含金属屏蔽层及铠装层两个外导体层，绝缘层采用交联聚乙烯材料．图1中为110,kV三相单芯埋地电缆，三相按“品”字形排布．

图1 6层结构三相单芯电缆结构

与架空线路类似，高压电力电缆传输方程为

   (1)

式中：、分别为三相电缆的电压、电流向量；、分别为三相电缆的串联阻抗矩阵和并联导纳矩阵．

根据文献[8]，图1中的每一相单芯电缆可按3个同轴等效回路进行分析，如图2所示．回路1由芯线与返回通路金属屏蔽层内表面组成；回路2由金属屏蔽层外表面与返回通路铠装层内表面组成；回路3由金属铠装层外表面与返回通路大地或海水组成．

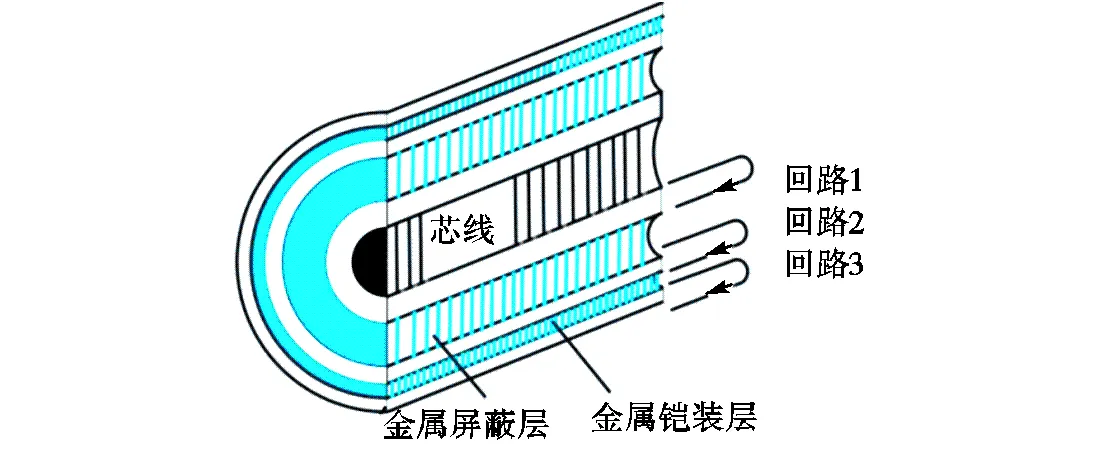
图2 6层结构单芯电缆等效回路示意

1.1 多层电缆阻抗矩阵计算方法

将式(1)中的阻抗方程按相进行分块，三相单芯电缆各回路电压、电流和阻抗的关系为

   (2)

以A相为例，单芯电缆中1、2、3回路中电压向量和电流向量分别为

   (3)

   (4)

考虑各回路间的电磁耦合作用，A相各回路的自阻抗矩阵为

   (5)

通常情况下埋地电缆的三相之间敷设间距较小，除一相内各回路间存在电磁耦合外，三相之间也存在电磁耦合．以A、B两相为例，由于回路3对回路1和2的屏蔽作用，两相相间的耦合只在回路3之间存在，因此A、B相间互阻抗矩阵为

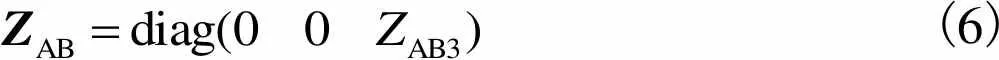
   (6)

同理可得其他各相自阻抗矩阵及两相相间互阻抗矩阵．具体回路阻抗的计算方法参见文献[8]．

因为电缆芯线等效阻抗的计算需根据各导体层电气量特性进行分析，所以下面研究将式(2)的回路方程变化为各导体层间的电气量关系方程的方法．

以A相为例，其芯线、屏蔽层及铠装层与回路1、2、3的电压电流关系为

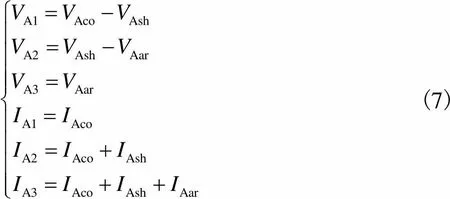
   (7)

将式(7)带入式(2)，消去各回路的电压、电流并按芯线、屏蔽层和铠装层进行矩阵分块，得到其电压、电流和阻抗的关系为

   (8)

各相芯线、屏蔽层及铠装层对地电压向量、电流向量具体为：；；；；；．

各相芯线阻抗矩阵为

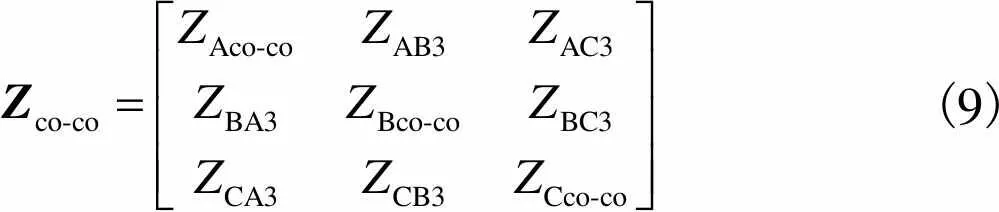
   (9)

各相屏蔽层阻抗矩阵为

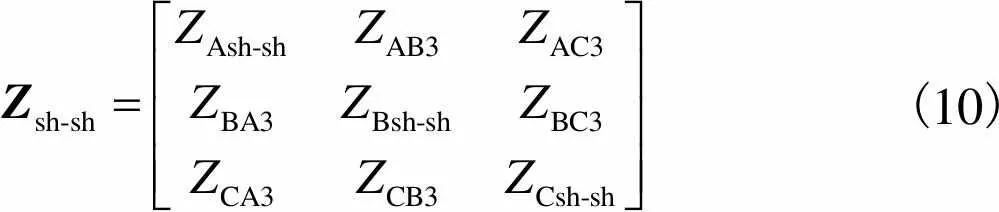
   (10)

各相铠装层阻抗矩阵为

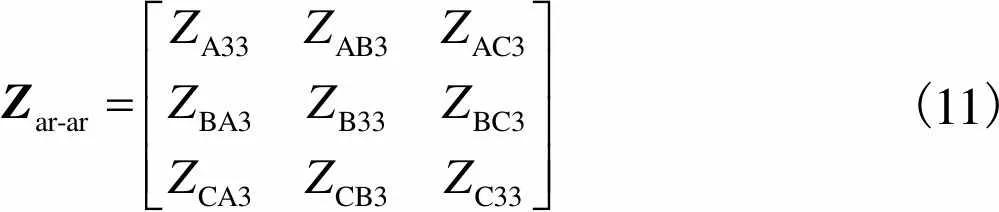
   (11)

各相芯线与屏蔽层间互阻抗矩阵为

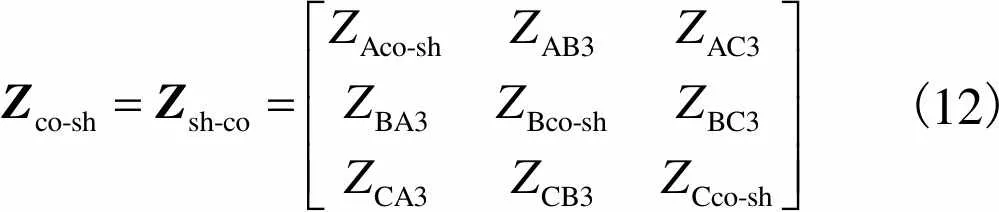
   (12)

各相芯线及屏蔽层与铠装层的互阻抗矩阵为

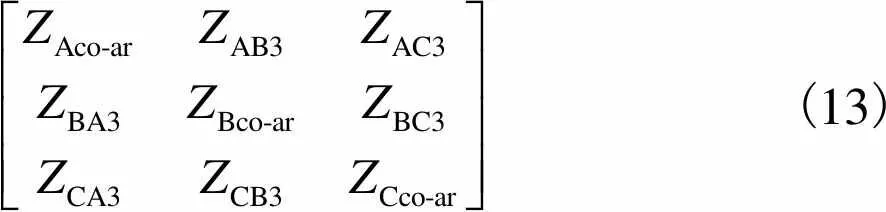
     (13)

1.2 多层电缆导纳矩阵计算方法

将式(1)中的导纳方程按相进行分块，三相单芯电缆各回路电压、电流和导纳的关系为

   (14)

由于大地或海水为等电位体，单芯电缆均外包有直接接地或海水的外导体层，因此各相之间不存在静电场的耦合，各非对角线导纳均为零矩阵[8]．

由图2中可以看出，各回路内部前行通道和返回通道之间为绝缘层，存在静电耦合；两回路之间为等电位金属层，不存在静电耦合，互导纳为零．以A相为例，各回路的自导纳矩阵为

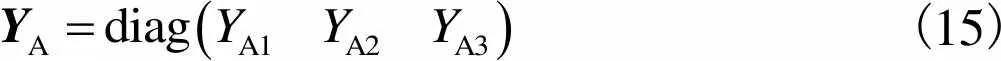
   (15)

同理可得其余各相回路的导纳矩阵．具体回路导纳的计算方法参见文献[8]．

将式(7)代入式(14)，消去各回路的电压、电流并按层进行矩阵分块，得到芯线、屏蔽层及铠装层的电压、电流和导纳的关系为

   (16)

其中，各相芯线自导纳矩阵为

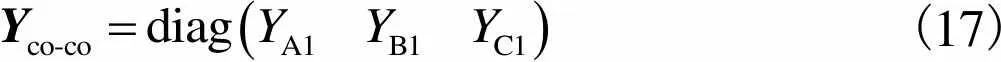
   (17)

各相屏蔽层自导纳矩阵为

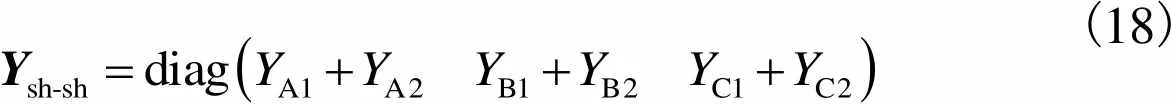
   (18)

各相铠装层自导纳矩阵为

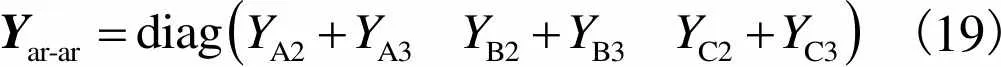
   (19)

各相芯线与屏蔽层间互导纳矩阵为

   (20)

各相屏蔽层与铠装层间互导纳矩阵为

   (21)

2 电缆芯线等效参数计算

由第1节分析可知，包含芯线、金属屏蔽层和铠装层的电缆阻抗和导纳均为9×9矩阵．通过分析金属屏蔽层和铠装层电气量的边界条件，可对9×9矩阵中的外导体层与芯线之间互感和电容进行消去，得到计及外导体层影响的电缆芯线等效阻抗和导纳矩阵为

   (22)

   (23)

2.1 电缆接地方式

电缆屏蔽层及铠装层电气量的边界条件取决于其接地方式．根据设计及运行规范，电力电缆通常采用一点接地、两端接地和交叉互联接地3种方式[9-13]，如图3～图5所示，其中一点接地包括端部接地和中点接地两种方式．

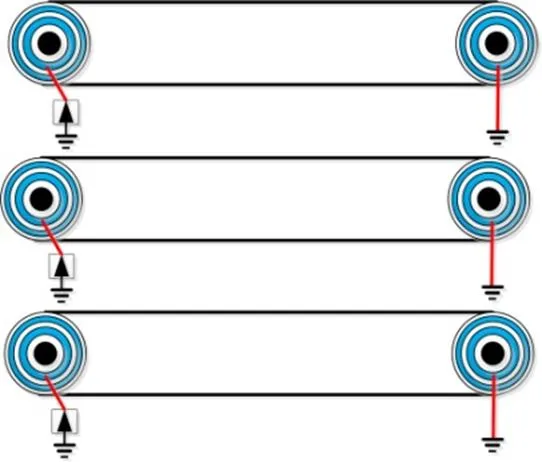
图3 电力电缆单端接地方式

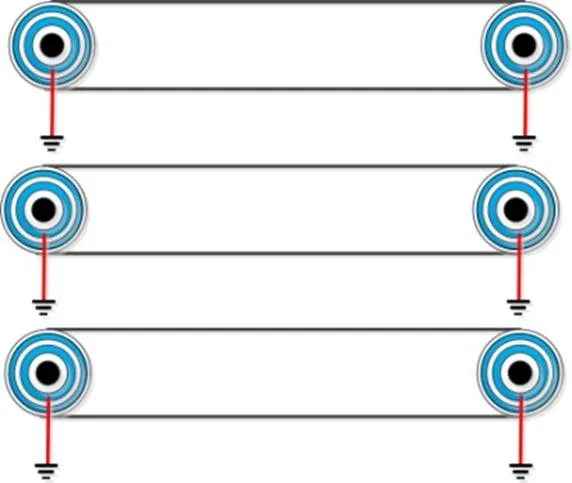
图4 电力电缆两端接地方式

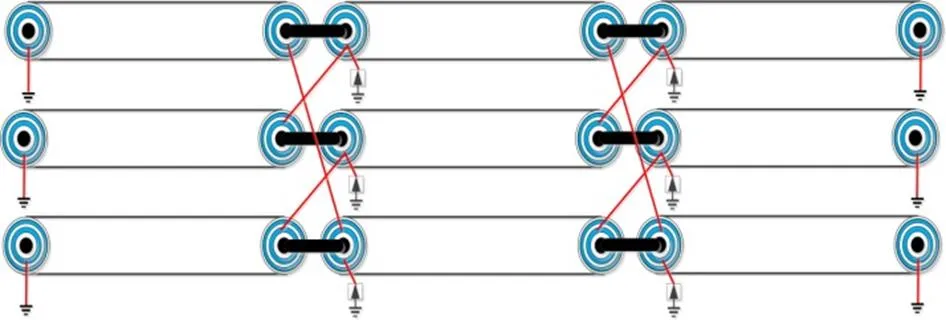
图5 电力电缆交叉互联接地方式

2.2 等效阻抗的计算

在高压电力电缆输送电能过程中，芯线电流会使外导体层产生感应电压，而外导体层接地方式的不同使其流过的电流也不相同．外导体层电流又会对芯线沿线电压产生影响，进而影响芯线的等效阻抗参数．下面分析上述不同接地方式下消除外导体层互阻抗影响的方法．

2.2.1 一点接地

不论电缆是端部接地还是中点接地，外导体层上均无电流回路，因此外导体层中电流为0，即

   (24)

将式(24)带入式(8)，可得

即

   (25)

与式(22)比较，可得计及外导体层影响的芯线等效阻抗矩阵

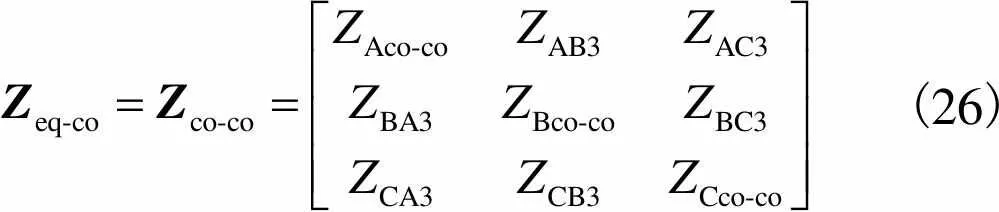
   (26)

可以看出，采用一点接地方式时，外导体层阻抗对芯线等效阻抗参数没有影响．

2.2.2 两端接地

电缆外导体层两端接地时，直接接地点电压为零，当接地点档距远小于研究频段的波长时，可认为外导体层沿线电位处处为零[14-16]，可得

   (27)

将式(27)带入(8)，可得

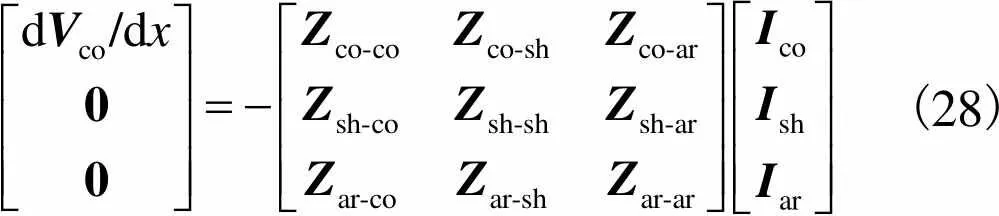
   (28)

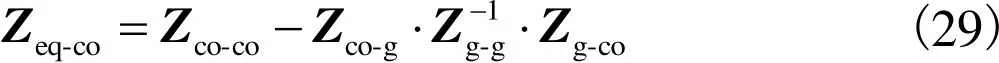
   (29)

2.2.3 交叉互联接地

当电缆采用图5所示的交叉互联接地时，首先将电缆自左(首端)向右(末端)逐段进行分析，再将3段进行整体等效化简．

第段屏蔽层首末端电压为

第段铠装层首末端电压为

流过第段屏蔽层及铠装层的电流分别为

第1段外导体层首端直接接地，因此可得

   (30)

第1段外导体层末端按A、B、C相顺序与第2段外导体层首端按C、A、B相顺序互联，因此可得

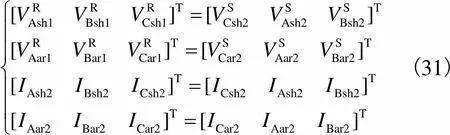
  (31)

第2段外导体层末端按A、B、C相顺序与第3段外导体层首端按C、A、B相顺序互联，因此可得

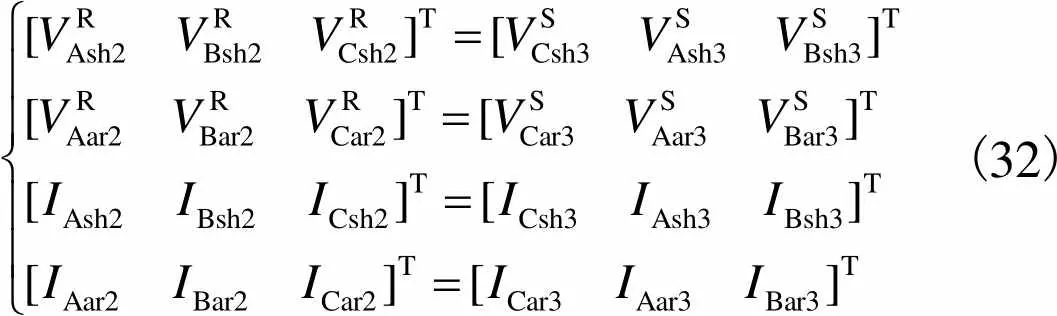
  (32)

第3段外导体层末端接地，因此可得

   (33)

假设每小段电缆长度为，考虑到其长度较短，每段电缆中外导体层电压变换率可近似表示为各段首、末两端的电压差与长度的比值，即

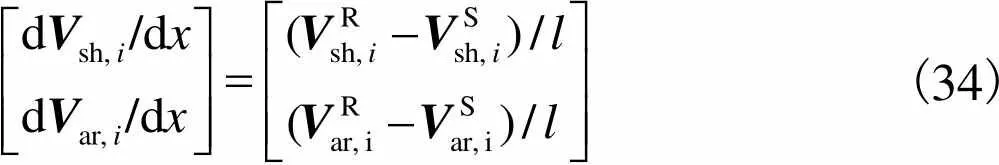
   (34)

电缆的外导体层经过3小段完成一个完全换位，且以3小段为整体将其两端直接接地．

将3小段作为整体分析即把式(30)～(34)带入式(8)，并消去3段的中间连接点处的电压、电流向量可得

   (35)

各分块阻抗矩阵具体表示如下.

芯线阻抗矩阵为

   (36)

屏蔽层阻抗矩阵为

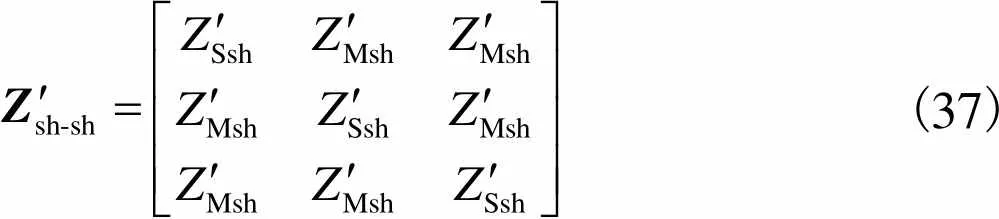
   (37)

铠装层阻抗矩阵为

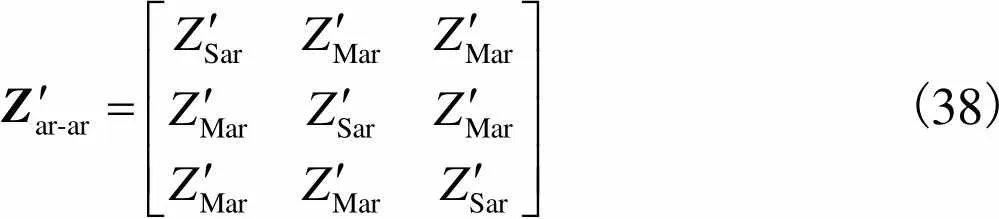
   (38)

芯线与屏蔽层之间的互阻抗矩阵为

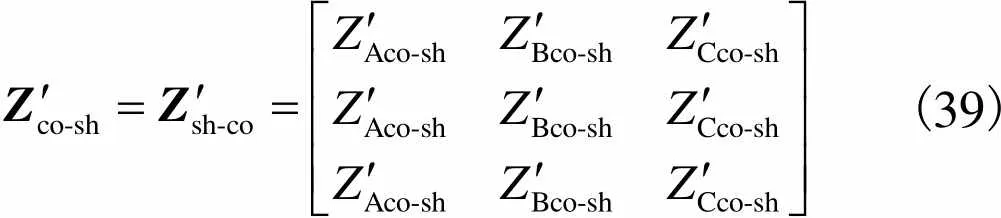
   (39)

芯线及屏蔽层与铠装层之间的互阻抗矩阵为

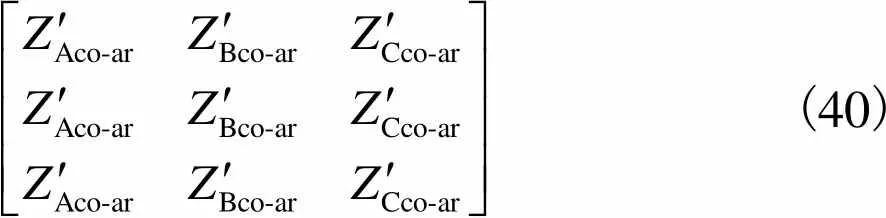
     (40)

   (41)

2.3 芯线等效导纳的计算

采用上述3种接地方式，在进行芯线等效导纳计算时都可认为外导体层电压近似为0[10]．将上述边界条件带入式(16)可知外导体层对芯线的导纳没有影响，三相电缆芯线等效导纳参数与芯线参数导纳相同，即

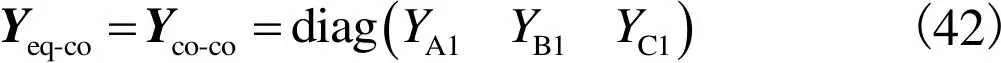
   (42)

针对其他不同层数的高压单芯电缆，由于其导体层均采用短距离焊接方式，可视为等电势体，因此其推导过程与本文6层结构单芯电缆相同．

3 仿真验证

本文采用PSCAD仿真软件对上述芯线等效阻抗和导纳矩阵计算方法的准确性进行验证．电缆采用频率相关模型，其基本结构和敷设方式如图1所示，具体几何尺寸如图6所示，C相埋设深度为0.5,m，相间距离为0.2,m，根据不同接地方式的要求，电缆的长度均取1.5,km．电缆芯线的电阻率为1.68×10-8,W·m，相对磁导率为1.0；外导体层的电阻率分别为2.2×10-7,W·m、1.8×10-7,W·m，相对磁导率分别为1.0和400.0；大地的电阻率为100W·m，相对磁导率为1.0．

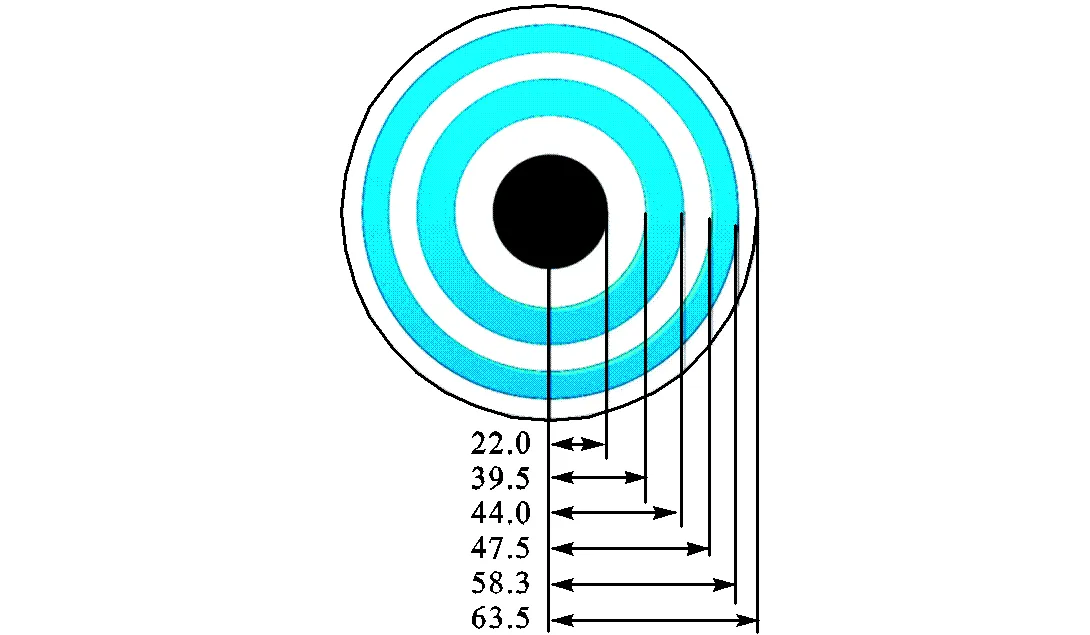
图6 6层结构单芯电缆几何尺寸

首先对不同接地方式下电缆的芯线端部电压电流进行测量，采用式(1)方程的向量形式计算得出芯线等效阻抗及导纳参数(称为测量值)．然后根据PSCAD线路几何模型的OUTPUT输出的工频阻抗及导纳矩阵参数，利用本文提出的方法计算得出进行芯线等效阻抗及导纳参数(称为计算值)．不同接地方式下测量值与计算值如表1～表4所示，其中误差为计算值与测量值相比的幅值绝对误差．

本文选取的三相单芯电缆为同一型号且呈品字形排布，因此芯线等效阻抗矩阵为对称矩阵且非对角线元素相等．由于埋设深度会对各相自阻抗产生影响，因此对角线元素有略微差别，本文采用三相自阻抗的平均值进行验证．

表1 一点接地方式下的等效阻抗参数

Tab.1 Equivalent impedance parameters under the con-dition of one end to earth

表2 两端接地方式下的等效阻抗参数

Tab.2 Equivalent impedance parameters under the con-dition of two ends to earth

表3 交叉互联接地方式下的等效阻抗参数

不同接地方式下的电缆导纳如表4所示，由于电缆的电导相比于电纳要小得多，因此在仿真验证中忽略电导，仅考虑芯线的自电纳参数．

表4 不同接地方式下的导纳参数

Tab.4 Admittance parameters under different grounding modes

由以上数据可以看出，在上述3种接地方式下，运用本文提出的芯线等效阻抗及导纳计算方法计算得到的结果与测量结果的误差不超过2.2%,，证明了算法的准确性．

4 结 语

高压电力电缆为多层结构，各导体层之间存在互感及电容耦合．本文研究了外导体层与芯线间的互感及电容对芯线参数的影响，分析了高压电力电缆的阻抗和导纳矩阵特征．针对电缆不同接地方式下的边界条件，提出了计及外导体层互感和电容影响的三相单芯电力电缆芯线等效阻抗和导纳的计算方法．PSCAD仿真验证表明本算法精度较高，能够满足电力系统计算和分析的需要．

［1］ Schelkunoff S. A. The electromagnetic theory of coaxial transmission lines and cylindrical shields[J].，1934，13(4)：532-579.

［2］ Ametani A. A general formulation of impedance and admittance of cables[J].，1980，99：902-910.

［3］ Matri L. Simulation of Electromagnetic Transients in Underground Cables with Frequency-Dependent Modal Transformation Matrices[D]. Vancouver：University of British Columbia，1986.

［4］ Wedepohl L M，Wilcox D J. Transient analysis of underground power-transmission systems：System-model and wave-propagation characteristics[J].，1973，120：253-260.

［5］ 毛为民. 电力电缆相序阻抗计算与分析[J]. 供用电，2002，19(4)：24-25.

Mao Weimin. Calculation and analysis of sequence impedance for power cable lines[J].，2002，19(4)：24-25(in Chinese).

［6］ 李长益，丁 伟. 高压电缆护层连接方式对线路参数的影响[J]. 江苏电机工程，2003，22(6)：22-23.

Li Changyi，Ding Wei. Effect of sheath connection form of high voltage cable to line parameters[J].，2003，22(6)：22-23(in Chinese).

［7］ 唐庆华，刘宝成，杨 洪，等. 高压电缆金属护套的接地方式对线路参数的影响[J]. 电线电缆，2009(2)：43-46.

Tang Qinghua，Liu Baocheng，Yang Hong，et al. Effect of the earthingmethod of the metal sheath in HV cables on line parameters[J].，2009(2)：43-46(in Chinese).

［8］ Dommel H W.[M]. Vancouver：Microtran Power System Analysis Corporation，1992.

［9］ Hill R J，Brillante S，Leonard P J. Electromagnetic field modeling for transmission line distributed parameters[J].，1999，146：53-59.

［10］ 中华人民共和国建设部. GB 50217—2007 电力工程电缆设计规范[S]. 北京：中国标准出版社，2007.

The Ministry of Construction of the People's Republic of China. GB 50217—2007 Cable Design Specification in Power Project[S]. Beijing：Standards Press of China，2007(in Chinese).

［11］ 欧景茹，祁树文，杨世春，等. 高压单芯电缆线路金属护套接地方式[J]. 吉林电力，2005(2)：19-21.

Ou Jingru，Qi Shuwen，Yang Shichun，et al. Grounding-protection means for metal tacket on high-voltage and single-core cable line[J].，2005(2)：19-21(in Chinese).

［12］ 刘志强，姜芸，李煜. 电力电缆线路参数测试技术的研究[J]. 高电压技术，2003，29(1)：10-11.

Liu Zhiqiang，Jiang Yun，Li Yu. Study on detection technique of power cable parameters[J].，2003，29(1)：10-11(in Chinese).

［13］ 王 波，罗进圣，黄宏新，等. 220,kV高压单芯电力电缆金属护套环流分析[J]. 高压电器，2009，45(5)：141-145.

Wang Bo，Luo Jinsheng，Huang Hongxin，et al. Analysis of circulating current in shealth of 220,kV XLPE single-core cable[J].，2009，45(5)：141-145(in Chinese).

［14］ 徐 政，钱 洁. 电缆电气参数不同计算方法及其比较[J]. 高电压技术，2013，39(3)：689-697.

Xu Zheng，Qian Jie. Comparison of different methods for calculating electrical parameters of power cables[J].，2013，39(3)：389-397(in Chinese).

［15］ 王育学，张 哲，尹项根，等. 平行多回电缆序阻抗参数的计算与分析[J]. 电网技术，2011，35(8)：186-191.

Wang Yuxue，Zhang Zhe，Yin Xianggen，et al. Calculation and analysis of sequence impedances for parallel multi-circuit cable lines[J].，2011，35(8)：186-191(in Chinese).

［16］ 田金虎，刘渝根，赵俊光，等. 多回同相多根并联高压电力电缆电流分布及金属护套环流计算[J]. 高电压技术，2014，40(1)：153-159.

Tian Jinhu，Liu Yugen，Zhao Junguang，et al. Circulating current in sheaths and current distribution on same-phase parallel multi-cable of multi-circuit power cable lines[J].，2014，40(1)：153-159(in Chinese).

(责任编辑：孙立华)

Calculation Method of Equivalent Core Impedance and Admittance Parameters of 3-Phase Single-Core Power Cable

Li Botong，Zhang Yunke

(Key Laboratory of Smart Grid of Ministry of Education，Tianjin University，Tianjin 300072，China)

Accurate core equiralent impedance and admittance parameters of power cable are required for relay protection setting and fault current calculation of power system with power cable．The characteristics of impedance and admittance matrix of three-phase single-core power cable were analyzed，taking into consideration the mutual inductance and capacitance coupling between core and conductive layers．The voltage and current boundary conditions of conductive layers in different grounding modes were presented．How to eliminate the influence of mutual inductance and capacitance of conductive layers on core parameters was studied in detail，and then the method for calculating three-phase single-core power cable core equivalent impedance and admittance parameters was proposed．The precision of the method was verified by PSCAD simulation tests in one end to earth mode，double-end to earth mode and cross bonding to earth mode.

single-core power cable；core；grounding mode；impedance matrix；admittance matrix

10.11784/tdxbz201507042

TM93

A

0493-2137(2016)11-1144-07

2015-07-13；

2016-01-25

国家自然科学基金资助项目(51207102)；高等学校博士学科点专项科研基金新教师类项目(20120032120085).

李博通（1981—  ），男，博士，副教授

李博通，libotong@tju．edu．cn

2016-03-11.

http://www.cnki.net/kcms/detail/12.1127.N.20160311.1511.004.html.