分组激振旋转超声电机弹性振动分析

王世宇，王尧尧



分组激振旋转超声电机弹性振动分析

王世宇1,2，王尧尧1

(1. 天津大学机械工程学院，天津 300072；2. 天津市非线性动力学与混沌控制重点实验室，天津 300072)

为解决电机受传统时空相位限制的这一难题，针对超声电机的激振问题，采用能量方法建立了定子弹性动力学模型．应用解析方法研究了压电片的分组对称拓扑对弹性振动特性的影响，揭示了拓扑结构与行波及驻波之间的映射关系，得到了产生行波的一般条件．结果表明：采用满足该映射关系的工作波数、压电片个数及其分组可生成期望的波动响应；该映射关系提供了保证振幅最大的压电片最优分组方式．研究结果有利于优化激振方式，提高超声定子的激振效率．

超声电机；分组对称；激振方式

旋转超声电机是一种机电一体化直接驱动装置．在过去20年中，该电机的研究取得了相当大的进展．但是，寿命、效率和稳定性问题一直未得到很好的解决．

传统旋转超声电机多为两相驱动．现有研究表明，若采用三相甚至多相，仍然可以激起行波[1]．但文献[2]指出：由于圆盘振子仅存在两个共振模态，因而三相激振不能产生稳定的旋转模态，除非进行强制振动，并允许机械品质因数低下时，才有可能激起稳定的旋转模态．文献[3]深入分析了三相激振问题，发现确实可以产生行波．文献[4]研究了多相驱动问题，比较了传统极化与对称极化分区的激振效果．结果表明，采用对称极化方式有利于激发工作模态，而且不易激发干扰模态．事实上，激励相数与共振模态个数本质上不同，因此能否激起行波与激励的时空相位匹配有关，只要采用合适的相位，三相激振同样可以产生稳定的行波．

应当指出的是，现有研究在分析两相或多相环型或盘型振子的行/驻波生成机理及振动特性时，通常采用简单的平板模型．由于模型过于简化，因而不利于深刻揭示基本运行原理，同时现有分析通常忽略谐波激励对电机性能的影响．

本文提出一种压电片分组拓扑结构，并分析基本激振原理，揭示压电片的拓扑方式与振动响应之间的映射关系，探讨压电片的合理分布问题．

1 数学建模

1.1 分析模型

本节拟建立环形超声定子的动力学模型，事实上现有文献已对该类环状结构开展了深入研究[5-9]，本节仅给出主要建模过程．图1为超声定子的动力学模型．图中和分别为切向和径向位移．假定压电片个数为(，为分组数，为组内压电片个数)，第个分组第个压电片的机械夹角及其相角分别为ψ, j＝ψ＋(－1)D和φ, j＝φ＋(–1)D(＝1，2，…，；＝1，2，…，)．其中和分别为第个压电片的机械夹角及其相角，和分别为相邻分组对应压电片之间的机械夹角及激励相位差．假定机械夹角与相角满足(为整数，表示时空相位比)．假定压电片对应圆心角为，定子支撑为，其与径向的夹角为．定子厚度、高度、刚度、中性圆半径、截面积分别为、、、和()．

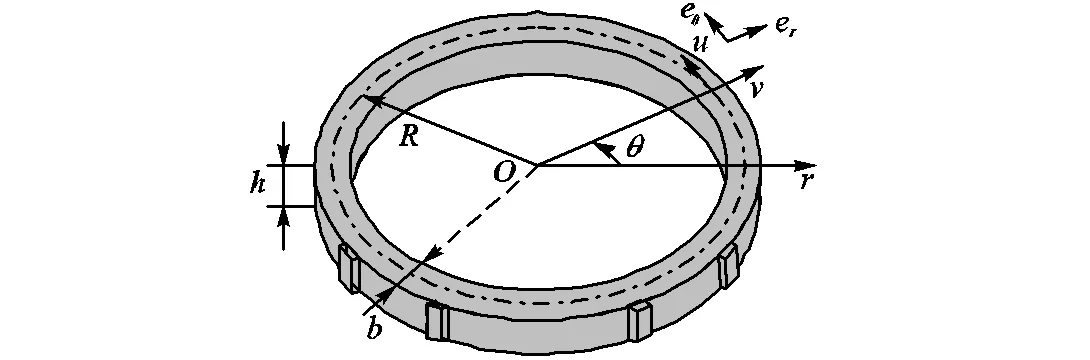
（a）定子

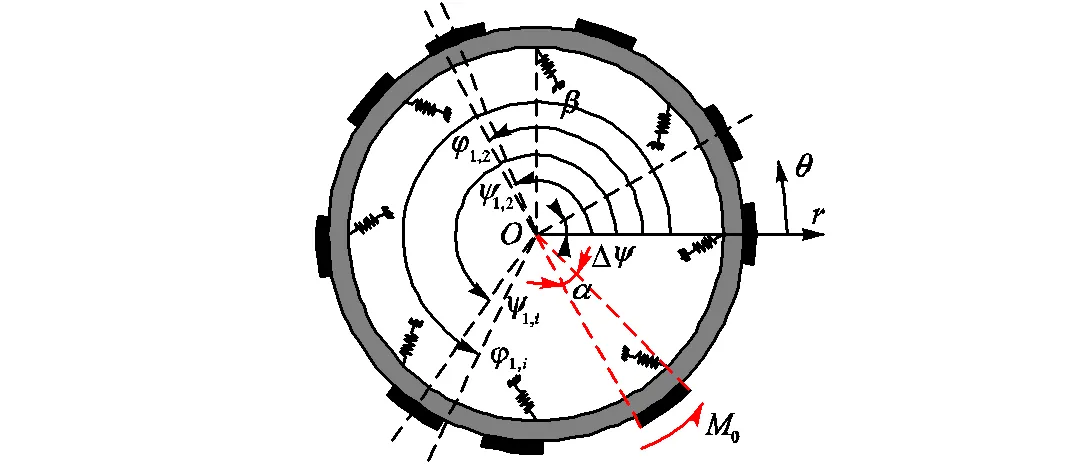
（b）坐标系

图1 分组激振超声定子及坐标系

Fig.1 Ultrasonic stator with grouped excitations and coordinates

1.2 数学建模

本文采用能量方法建模．在计算能量时，忽略压电片影响，仅考虑定子动能、定子势能和压电片弯曲能量．定子上坐标为()质点的切向位移[7]为

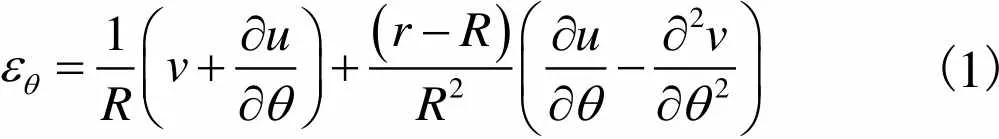
   (1)

定子势能可写为

定子动能为

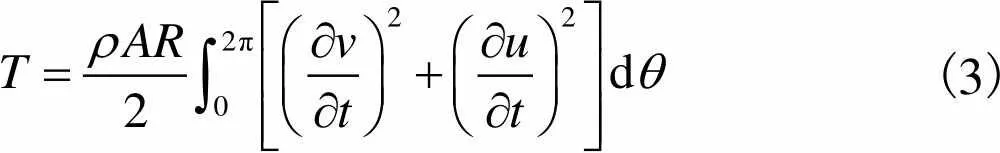
   (3)

弹性支撑势能为

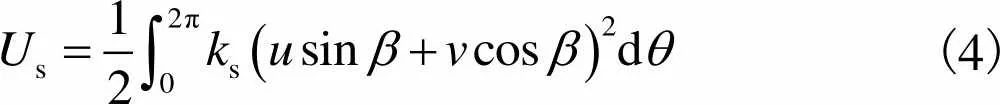
   (4)

压电片产生的弯矩[10]为

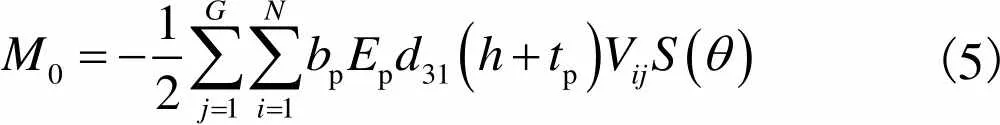
   (5)

其中

   (6)

弯矩做功为

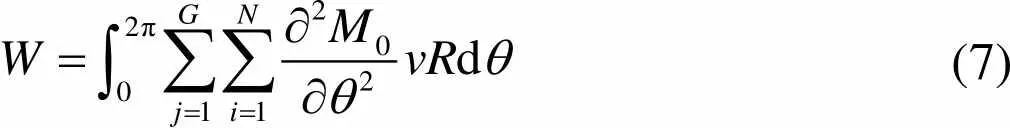
   (7)

根据哈密顿原理有

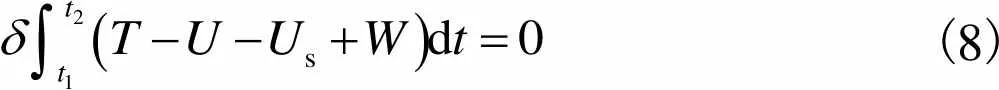
   (8)

代入式(2)～式(4)和式(7)，整理后可得动力学方程．引入无量纲运算()、和，改写方程，并将、和分别用、和代替，可得无量纲受迫振动方程为

   (9)

2 模型求解

采用一项伽辽金离散式(9)，可得

   (10)

   (11)

与式(11)对应的自由振动方程为

   (12)

假设

   (13)

经求解可得正则振型

   (14)

其中

引入正则变换

并将其代入式(11)可得

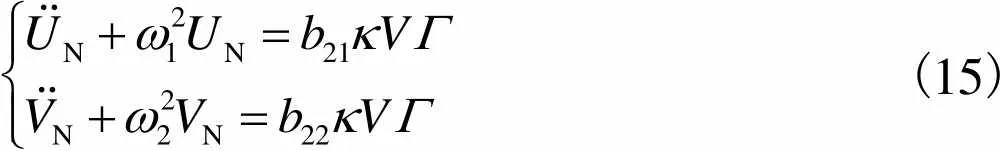
   (15)

假设

   (16)

将式(16)代入式(15)可得

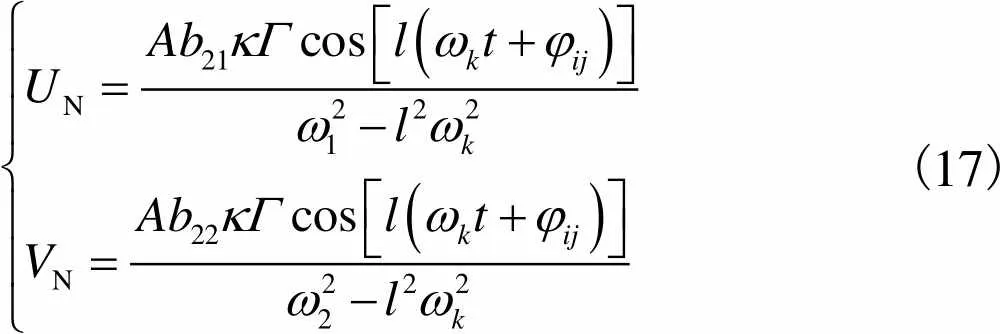
   (17)

经逆变换可得

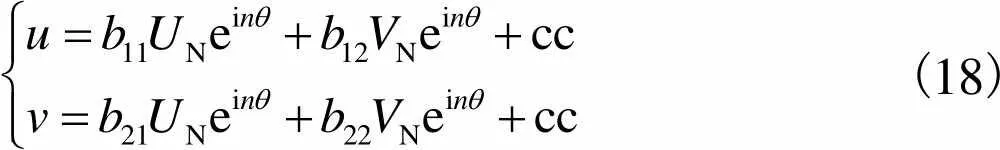
   (18)

分析式(18)可知，若波数、谐波阶次、时空相位及压电片分组数满足一定条件，则定子将产生不同的响应．根据式(18)及不同的参数组合条件，可得如下3种典型响应.

   (19)

其中

显然，此时激起正向行波响应．

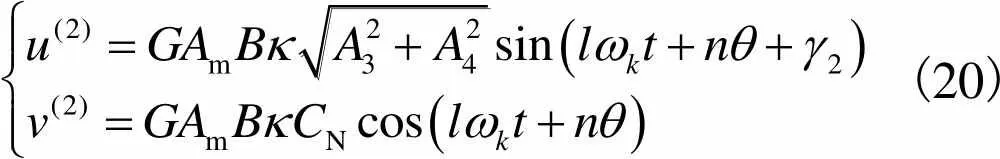
   (20)

其中

在该激振条件下，定子的响应为反向行波．

   (21)

在该激振条件下，响应为驻波．

3 仿真计算及验证

本文揭示了分组对称激励方式与响应之间的映射关系．本节以螺母型超声电机定子[11]为例，对上述解析结论进行对比验证，并给出仿真计算．表1为该电机的基本参数，其中径厚比满足薄环条件．图2为3种典型激振方式．需要指出的是，尽管上述参数与文献[11]可能不同，但不影响本文验证．

表1 基本参数

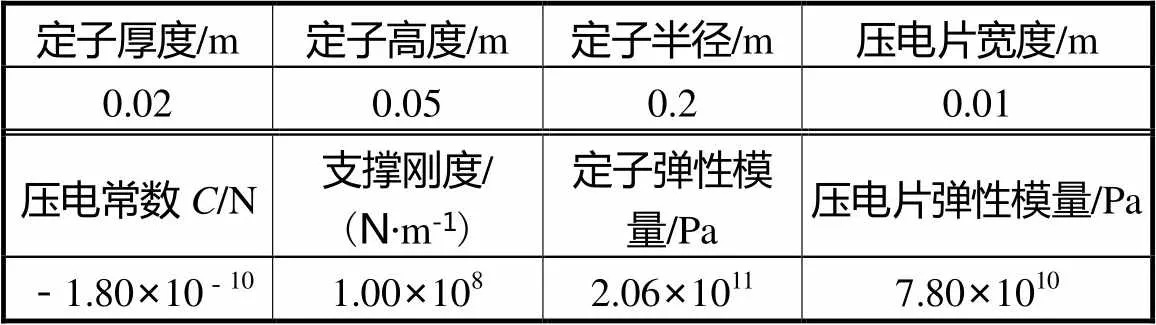
Tab.1 Specifications

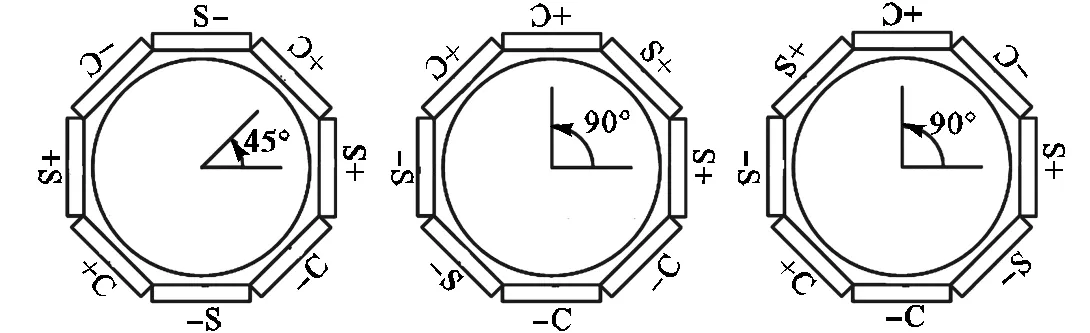
（a）方案A(＝2)  （b）方案B(＝3) （c）方案C(＝3)

图2 3种典型激振方案

Fig.2 Three typical excitation patterns

文献[11]采用了驻波叠加方法分析了超声定子的振动特性，给出了可生成行波的激振信号序列．本文采用严格的数学分析得到了定子的振动响应．考虑超声电机的容性效应[12]，仅取第1阶谐波激励对图2所示3种激振方案进行振动预测．经分析可得分组数、组内压电片个数、组内相邻压电片机械夹角及相位差之间的关系，如表2所述．

表2 参数组合

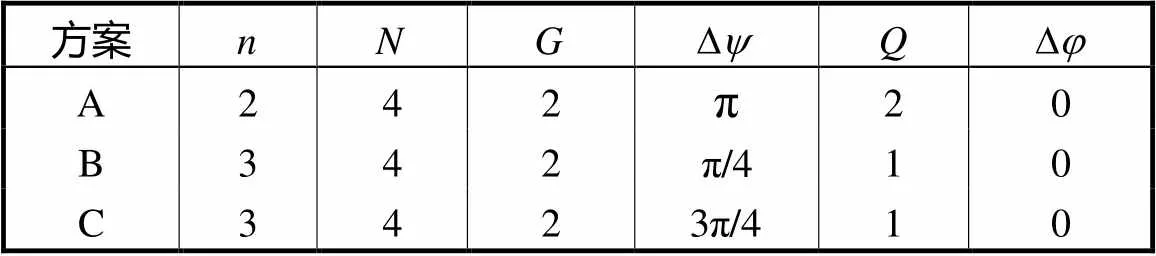
Tab.2 Parameter combinations

3个方案的参数组合分别为{，，，，}＝{2，4，1，2，2}、{3，4，1，1，2}和{3，4，1，1，2}．简单分析可知，均有为整数，且不为整数，根据式(19)可知，3个方案均可激起正向行波．进一步分析可知，对于不同的激励相位，响应的差别仅体现于系数．因此本节仅用该值来衡量激振效果．经计算，3个方案的系数取值分别为2、和．显然，在相同波数下，方案C的激振效果最显著．图3为方案B和C对应不同激振频率的切向及径向响应，图中尖峰位置对应固有频率．显然，方案C的激振效果总体上优于方案B，与上述解析预测一致．因此验证了式(19)所得结论的正确性．

（a）切向响应

（b）径向响应

图3 方案B与C激振幅值比较

Fig.3 Comparison between amplitudes of cases B and C

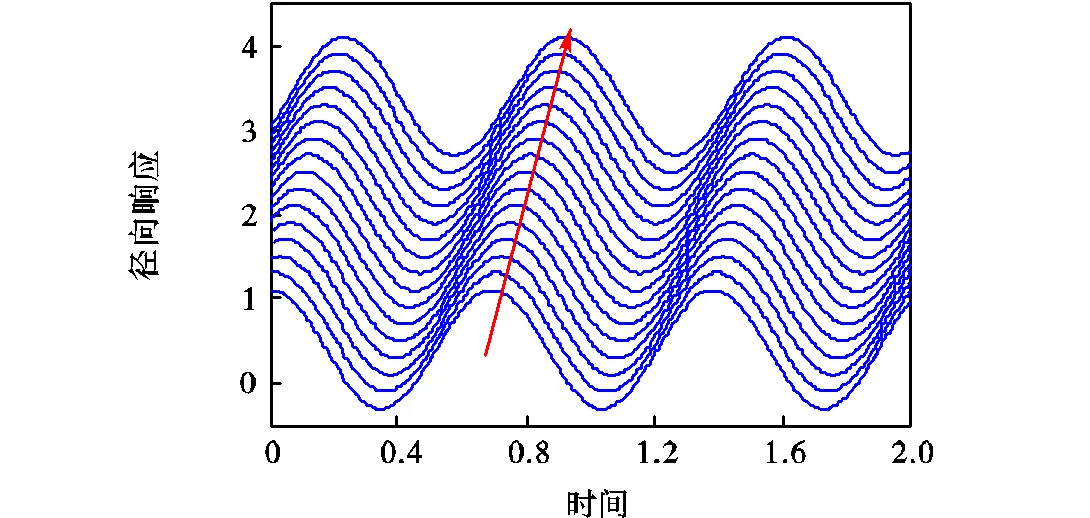
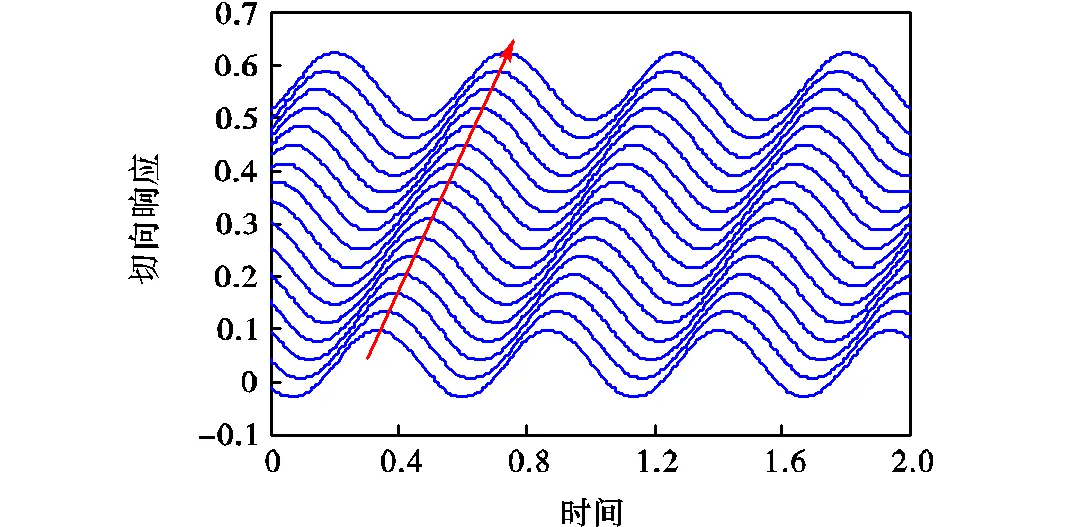
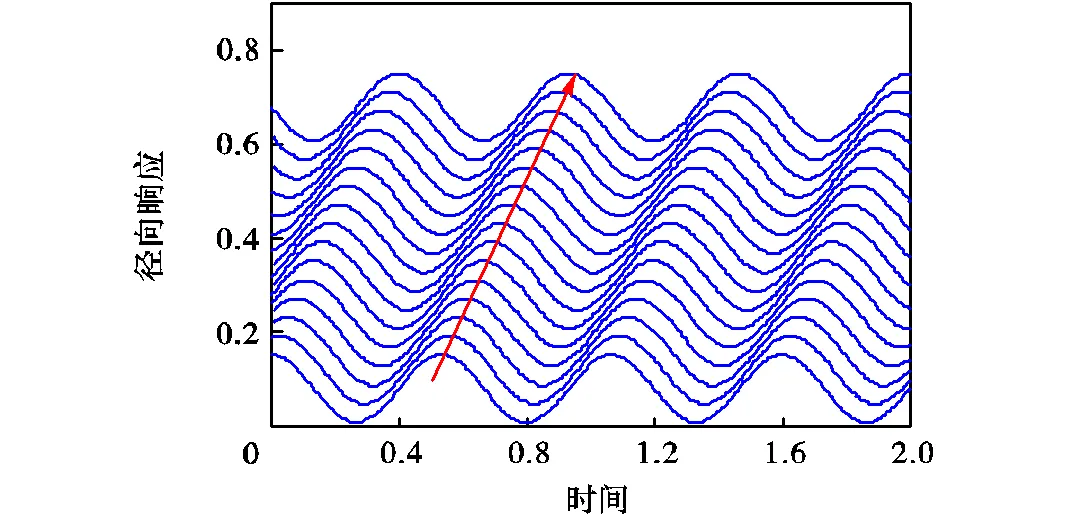
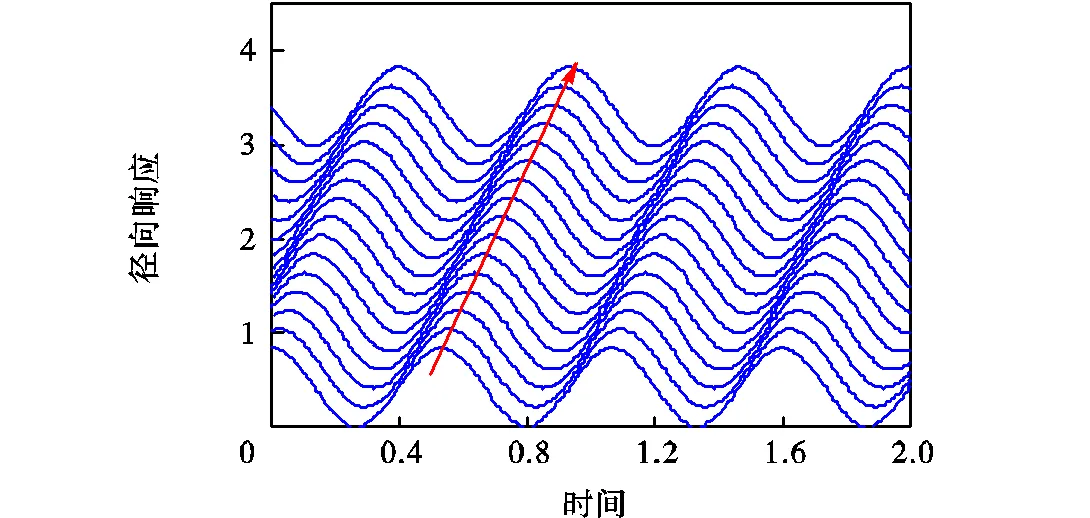
图4～图6为激振频率为110的切向及径向时域响应，为了清晰地显示波动效果，本文给出了均匀分布于定子的16个位置的时域响应．由于参数组合满足第1种典型响应的条件，3个方案均激起正向行波，其中图4对应传统的时空相位，而图5和图6的时空相位均为90°，并且方案C的振幅最大．因此，图4～图6所示与式(19)所预测的响应一致，证明了本文揭示的激振相位的正确性及其激振效果．

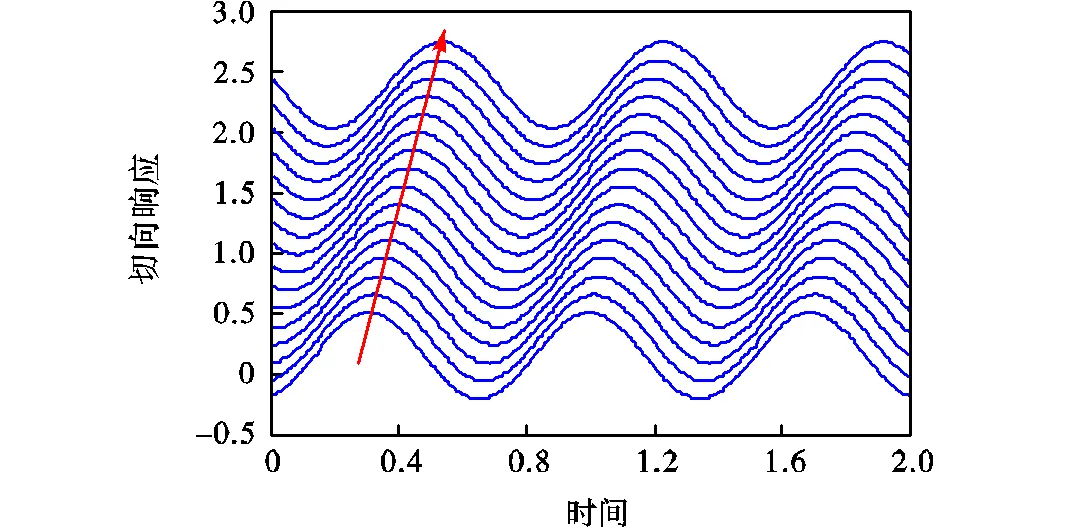
（a）切向响应

（b）径向响应

图4 方案A定子时域响应(＝2，Dy＝p)

Fig.4 Stator time dormain reponse of case A(＝2，Dy＝p)

（a）切向响应

（b）径向响应

图5 方案B定子时域响应(＝3，Dy＝p/4)

Fig.5 Stator time dormain reponse of case B(＝3，Dy＝p/4)

（a）切向响应

（b）径向响应

图6 方案C定子时域响应(＝3，Dy＝3p/4)

Fig.6 Stator time dormain reponse of case C(＝3，Dy＝3p/4)

4 工程应用

本文根据超声电机的结构及激振的对称性，以环形振子为例，采用严格的解析方法得到了一般激振条件，同时探讨了提高激振效率的激振方式．研究结果表明，如果工作波数、组内压电片个数及时空相位比等基本参数满足为整数，即可激起期望的振动．具体而言，在工程实际中可适当组合3个参数，即可激起前行波(为整数)、后行波(为整数)或驻波(均为整数)．同时，还可以根据式(18)～式(20)中的系数～，进一步调整时空激振相位，以提高驱动效率．上述条件还表明，多相激振可生成期望的行/驻波，而且不限于传统的90°时空相位．

5 结 论

(1) 采用能量方法建立了超声定子的机电耦联动力学模型，并采用解析方法对其进行求解．

(2) 揭示了压电片分组对称方式与振动响应之间的映射关系，给出了行波的一般激振条件．

(3) 为了提高激振效率，给出了可激起较大振幅的时间相位及空间相位的最优组合方式．

(4) 与文献[11]对比证明了所得一般激振方法以及最优时空相位激振条件的正确性和有效性．

［1］ 董云朝，刘景全，杨志刚，等. 圆筒压电振子产生周向行波的激励原理[J]. 压电与声光，2002，24(1)：64-67.

Dong Yunzhao，Liu Jingquan，Yang Zhigang，et al. Traveling-wave exciting principle of cylindrical vibrator in circumferential direction[J].，2002，24(1)：64-67(in Chinese).

［2］ 上羽贞行，富川义郎. 超声波马达理论与应用[M]. 杨志刚，译. 上海：上海科学技术出版社，1998.

Ueha S，Tomikawa Y.：[M]. Yang Zhigang，Trans. Shanghai：Shanghai Science Press，1998(in Chinese).

［3］ 曹 辉，林书玉. 三相驱动的平板弯曲行波超声马达研究[J]. 陕西师范大学学报：自然科学版，2005，33(2)：46-48.

Cao Hui，Lin Shuyu. Flexural vibration ultrasonic motor of plain plate of travelling wave of three-phase drive[J].：，2005，33(2)：46-48(in Chinese).

［4］ 赵淳生. 超声电机技术与应用[M]. 北京：科学出版社，2007.

Zhao Chunsheng.[M]. Beijing：Science Press，2007(in Chinese).

［5］ Huang S C，Soedel W. Effects of Coriolis acceleration on the free and forced in-plane vibration of rotating rings on elastic foundation[J].，1987，115(2)：253-274.

［6］ Xie Bang，Wang Shiyu，Wang Yaoyao，et al. Magnetically induced rotor vibration in dual-stator permanent magnet motors[J].，2015，30(3)：390-396.

［7］ Zhao Zhifu，Wang Shiyu. Parametric instability induced by traveling magnetic load within permanent magnet motors[J].，2015，80(1/2)：827-843.

［8］ Zhao Zhifu，Wang Shiyu. Parametric instability of dual-ring structure with motionless and moving supports[J].，2016，11：014501-1-14501-9.

［9］ 王世宇，陈东亮，刘建平，等. 分组对称旋转周期结构固有频率分裂解析模型[J]. 天津大学学报，2012，45(5)：393-399.

Wang Shiyu，Chen Dongliang，Liu Jianping，et al. Analytical analysis on natural frequency splitting of rotationally periodic structure with grouped features[J].，2012，45(5)：393-399(in Chinese).

［10］ Dadfarnia M，Jalili N，Dawson D M. A Lyapunov-based piezoelectric controller for flexible Cartesian robot manipulators[J].，，，2004，126(2)：347-358.

［11］ Zhou T Y，Zhang J，Chen Y. A nut-type ultrasonic motor and its application on focus system[C]//，. Beijing，China，2009：914-920.

［12］ 夏长亮，杨 荣，祁温雅，等. 液体媒质超声波电机驱动系统[J]. 天津大学学报，2005，38(1)：5-8.

Xia Changliang，Yang Rong，Qi Wenya，et al. Driving system of the ultrasonic motor driving fluid directly[J].，2005，38(1)：5-8(in Chinese).

(责任编辑：孙立华)

Elastic Vibration Analysis of Rotary Ultrasonic Motors with Grouping Excitations

Wang Shiyu1,2，Wang Yaoyao1

(1．School of Mechanical Engineering，Tianjin University，Tianjin 300072，China；2．Tianjin Key Laboratory of Nonlinear Dynamics and Chaos Control，Tianjin 300072，China)

The vibration excitation of ultrasonic motor is examined in this paper．In order to improve the efficiency of the traditional motor，an elastic dynamic model of stator was developed by using energy method．The effect of grouping symmetric topology on vibration properties was analytically examined．The mapping relationships and conditions between the topology and traveling/standing wave were identified and the general conditions of traveling wave occurrence were obtained．The results imply that desired wave vibration can be aroused by using a suitable parameter combination satisfying the mapping relationships，where the parameters include the working wavenumber，number of piezoelectric patches and grouping pattern．Thus an optimized grouping pattern inducing remarkable amplitude is obtained．The results contribute to improve the excitation pattern and enhance the excitation efficiency of stator.

ultrasonic motor；grouping symmetry；excitation patterns

10.11784/tdxbz201505059

TK421

A

0493-2137(2016)11-1203-06

2015-05-14；

2015-10-16.

国家自然科学基金资助项目(51175370)；天津市应用基础与前沿技术研究计划重点资助项目(13JCZDJC34300).

王世宇（1974—  ），男，博士，副教授.

王世宇，wangshiyu@tju.edu.cn.

2015-12-07.

http://www.cnki.net/kcms/detail/12.1127.N.20151207.0938.004.html.