单层隔振系统中塑性限位器应用设计

韩　阳，谌　勇，陈　锋

单层隔振系统中塑性限位器应用设计

韩阳，谌勇，陈锋

（上海交通大学 机械系统与振动国家重点实验室，上海 200240）

提出舰船单层隔振系统中采用以聚氨酯泡沫为材料的限位器进行设备限位，研究塑性限位器各参数对舰船设备最大加速度和最大相对位移这两个重要指标的影响，提出确定限位器参数理论方法，采用Matlab软件将塑性限位器理论量化方法和设计计算程序用于单层隔振系统模型，并进行冲击实验，证明该理论方法的正确性。

振动与波；聚氨酯；限位器；冲击

舰船作为水面或水下各种作战装备平台，容易遭受导弹、鱼雷及航空炸弹等各种反舰兵器的攻击［1-3］，其主要威胁来自于水中非接触性爆炸，爆炸冲击波会对舰船设备产生强烈的冲击作用［4］。传统的隔振抗冲击元件往往不能满足系统的抗冲击性能要求，而且大多数情况下进行系统设计时很少考虑其抗冲击能力，使得系统的抗冲击性能不足。因此对隔振系统的抗冲击性能研究以及新型隔振抗冲击元器件的开发是非常必要的。

虽然大多数舰船设备采用了隔振装置，但是由于隔振装置的固有频率一般较低，所以在冲击载荷作用下，设备承受的加速度一般都不大，一般船用机械设备都能满足要求，而设备所承受的冲击位移可能超出容许范围，甚至超出了限位器本身的极限变形能力，导致限位器被破坏或产生刚性接触。因此，如何限制设备的最大相对位移就显得尤为重要。简单地在设备上安装限位器来限制设备的位移，是最直接也最有效的方法之一。

限位器有一定的工作间隙，在设备正常工作时限位器不起作用，对系统没有影响，当设备的位移响应达到一定值时，限位器起作用，限制设备的最大相对位移响应［5］。刚性限位器虽然可以起到限制设备相对位移的作用，但是在承受强冲击作用时，如果限位器不破坏，将会造成极大的二次冲击，具体表现为设备的加速度响应急剧增加。因此，限位器也必须具有一定的柔度，避免在限制设备的位移时使系统产生过大的二次冲击。弹性限位器可以大幅减少系统产生的二次冲击，但代价是其限制设备相对位移的能力下降，因此弹性限位器抗冲击的效果打了很大的折扣。

基于这种情况，本文提出了将采用以聚氨酯泡沫为材料的塑性限位器［6］应用到单层隔振系统中，首先通过理论分析，得出塑性限位器结构参数和工作间隙的理论设计方法，并应用理论设计方法对单层抗冲击模型进行设计计算，接着应用Matlab软件，采用时域直接积分法对系统模型进行仿真分析计算，并对系统模型进行抗冲实验，通过该方法设计塑性限位器的正确性。

1　理论分析

1.1材料本构模型

引入的塑性限位器以泡沫材料为主，弹塑性体压缩应力-应变曲线如图1所示。

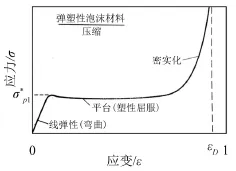
图1　弹塑性体压缩应力-应变

根据文献［7］，当弹性体泡沫材料受到压缩时，它首先以线弹性的方式发生变形，然后它的孔穴产生屈曲，导致非线弹性，最后，孔穴完全坍塌破坏，且随着孔面和孔棱压在一起，其应力急剧上升。塑性泡沫材料的表现方式与此相似，除了线弹性后紧接着是塑性坍塌破坏而不是弹性屈曲。对于脆性泡沫材料，由于其平台期应力不稳定，不利于对限位器参数的定量分析，故本文中不讨论。另外，由于泡沫材料结构复杂，力学影响因子较多，故本文提取了部分对限位器设计起主要作用的参数，并对其压缩应力-应变曲线进行了简化处理。

选取一种弹性或弹塑性泡沫材料，其屈服强度和密实化应变为

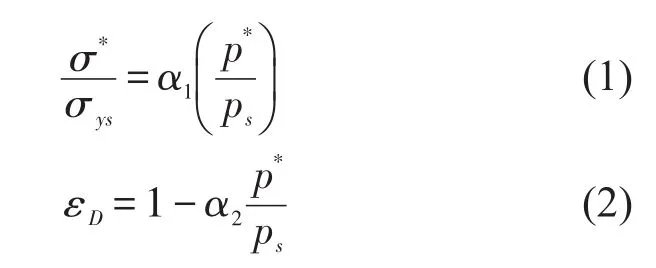
式中σ*为该材料的弹性屈曲应力或塑性坍塌应力，也可称为平台应力；σys为孔壁材料的屈服强度；p*/ ps为泡沫体本身的相对密度。

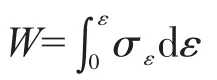
1.2限位器参数分析

塑性限位器物理模型如图1所示，质量为m的设备由支撑刚度为k的单层隔振系统支撑，假定冲击作用为基础的半正弦波加速度输入，幅值为Fa，脉宽为τ。限位器的主要参数是工作间隙U0和结构参数：高度H，横截面积S，本文中限位器为圆柱体，所以其主要参数为截面半径R。

图2　塑性限位器物理模型

为了方便计算，将加速度积分得到冲击结束后基础获得的初速度V0

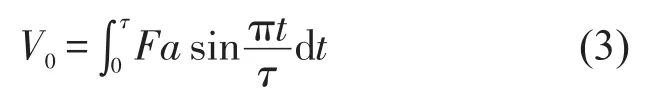
根据文献［8-10］，在没有塑性限位器的情况下，设备的最大响应为

式中Xm0为设备在无聚氨酯限位器下的最大位移，am0的最大加速度值。

在有限位器的情况下，通常U0＜Xm0（否则限位器不起作用），由于冲击时间很短，不考虑阻尼的作用，不考虑限位器碰撞过程中的能量损耗，那么在整个冲击作用的响应过程中机械能守恒。

没有限位器和有限位器时，冲击载荷输入系统的能量为

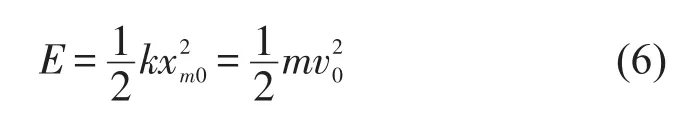
因此，在有塑性限位器且其起作用时有如下的关系

式中σ是聚氨酯平台期应力。

令 f=σS，由上式可得

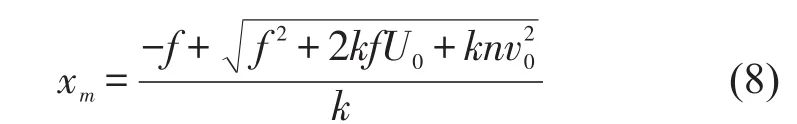
式中xm为设备在有塑性限位器情况下的最大相对位移，am为设备在有塑性限位器情况下的最大加速度。

采用无量纲的量

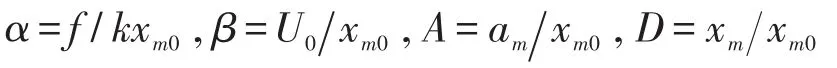
来表示上两式，可得

由上两式可以表示设备的最大相对位移、最大加速度随限位器参数变化的曲线，见图3（a）、图3（b）。

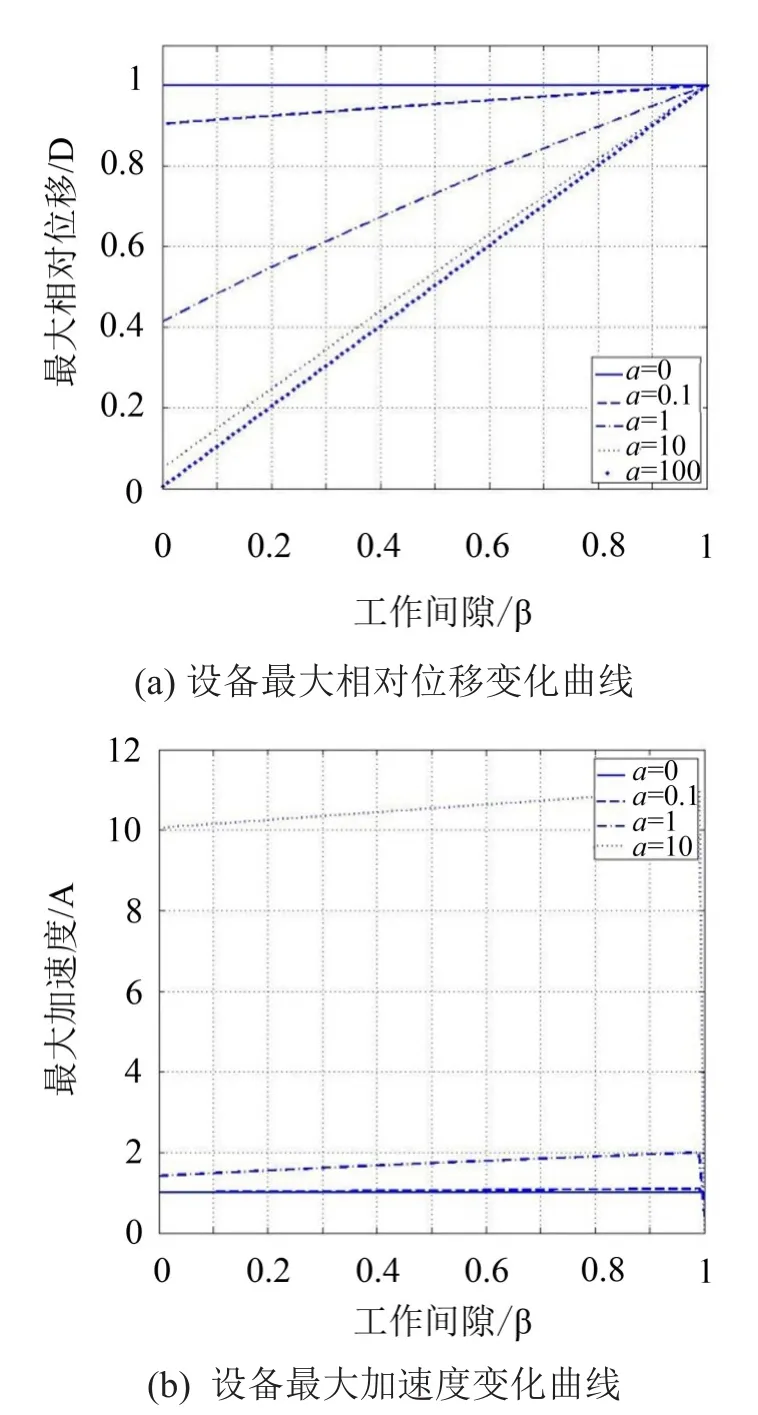
图3　设备响应随限位器参数变化关系

图3中（a）、（b）分别为不同应力的限位器在不同工作间隙U0下设备的最大相对位移D和最大加速度A。限位器的参数α分别为0、0.1、1、10和100。

由参数α本身的性质可知：在确定了设备在无限位器下的最大位移xm0和隔振器刚度k后，α越大表示设备接触限位器时所受的反作用力越大。由图可知：限位器的工作间隙和刚度直接影响最大位移与最大加速度，当α大于100时，最大位移几乎和工作间隙成正比，而加速度增大的幅度和α增大的幅度相当。限位器的f增加可以减少最大相对位移，但随着刚度的增加，最大加速度急剧增加，而最大位移减小不多，因此f不应过大。对于某一α值，从图3（b）中可以看出，增大工作间隙，最大加速度A的增大很小，因此在设计时主要关注的是工作间隙对最大相对位移D的影响。另外需要注意的是，为了不影响隔振器的正常隔振效果，限位器的工作间隙不能过小，需要满足一定要求。

在设计隔振装置时，若选用刚性限位器，即图中α→∞时的情况，此时设备的最大相对位移与限位器的工作间隙相同，而设备的最大加速度会随着工作间隙的减小而急剧增大。因此，为了避免限位器在冲击作用时对系统产生过大的冲击力和限位器的二次冲击，在选用限位器时应选用塑性限位器。

1.3限位器参数设计

在设计隔振装置时，首先根据隔振要求来确定隔振器刚度，然后根据抗冲击要求（相对位移和加速度）来确定限位器参数。

对于单层隔振装置，具体的塑性限位器参数设计过程为：1.设计根据系统的隔振要求来确定隔振系统的支撑刚度k。2.根据设备实际使用情况中要求的最大位移限制或者隔振器的极限变形能力来确定允许的设备最大相地位移xm；根据设备的实际情况，确定允许的最大加速度am。3.根据冲击激励和隔振系统的支撑刚度计算出没有限位器时设备的最大相对位移响应xm0和最大加速度响应am0。4.通过上述参数计算出无量纲最大相对位移D和最大加速度A，求解方程得到无量纲参数α和β，即可确定限位器的工作间隙U0，f确定后，通过选择不同相对密度的聚氨酯，即选择不同的σ，最终可以确定限位器的横截面积，即确定截面半径R。

塑性限位器的设计目标是，满足最大相对位移的前提下，通过设计塑性限位器的f，使设备的冲击加速度相对较小，由于塑性限位器是在设备相对位移超过允许值之前进行预先的限位，需要有一个限位吸收能量的过程，因此塑性限位器势必会减小隔振器的正常隔振位移范围，但是通过合理的设计f，这种影响会降低到最低。

2　模型算例

模型算例是一个单层隔振系统，采用上述方法对该单层隔振装置需选用的塑性限位器进行理论设计，主要确定限位器的参数即工作间隙和f，并用Abaqus和Matlab分别对使用和不使用塑性限位器的隔振系统进行冲击响应计算，从而对比限位器的使用效果以及验证限位器参数的可行性。算例仅确定限位器的垂向参数，横向和纵向参数的确定方法相同。

算例的单层隔振装置中设备重40 kg，所选用的隔振器刚度为100 000 N/m。采用Abaqus大型有限元分析软件对系统进行瞬态响应分析。计算中给定的加速度激励为半正弦时间历程，其中加速度幅值为200 m/s2，加速度激励脉冲宽度为6 ms。计算中加速度激励作用于系统的垂向，横向以及纵向激励时的计算与垂向激励时的计算方法相同。

首先用Abaqus对系统进行响应分析［11］，系统模型如图所示。

图4　有限元模型

为了简化模型，设备和基础均为刚体，设备和基础由4个隔振器连接，圆柱形限位器位于中心，采用显示动力学分析其0.2 s内的时域响应。然后用Matlab对系统进行动力学建模，采用4阶龙格-库塔法直接积分求解。Abaqus有限元仿真结果与Matlab动力学模型求解结果对比如图所示。

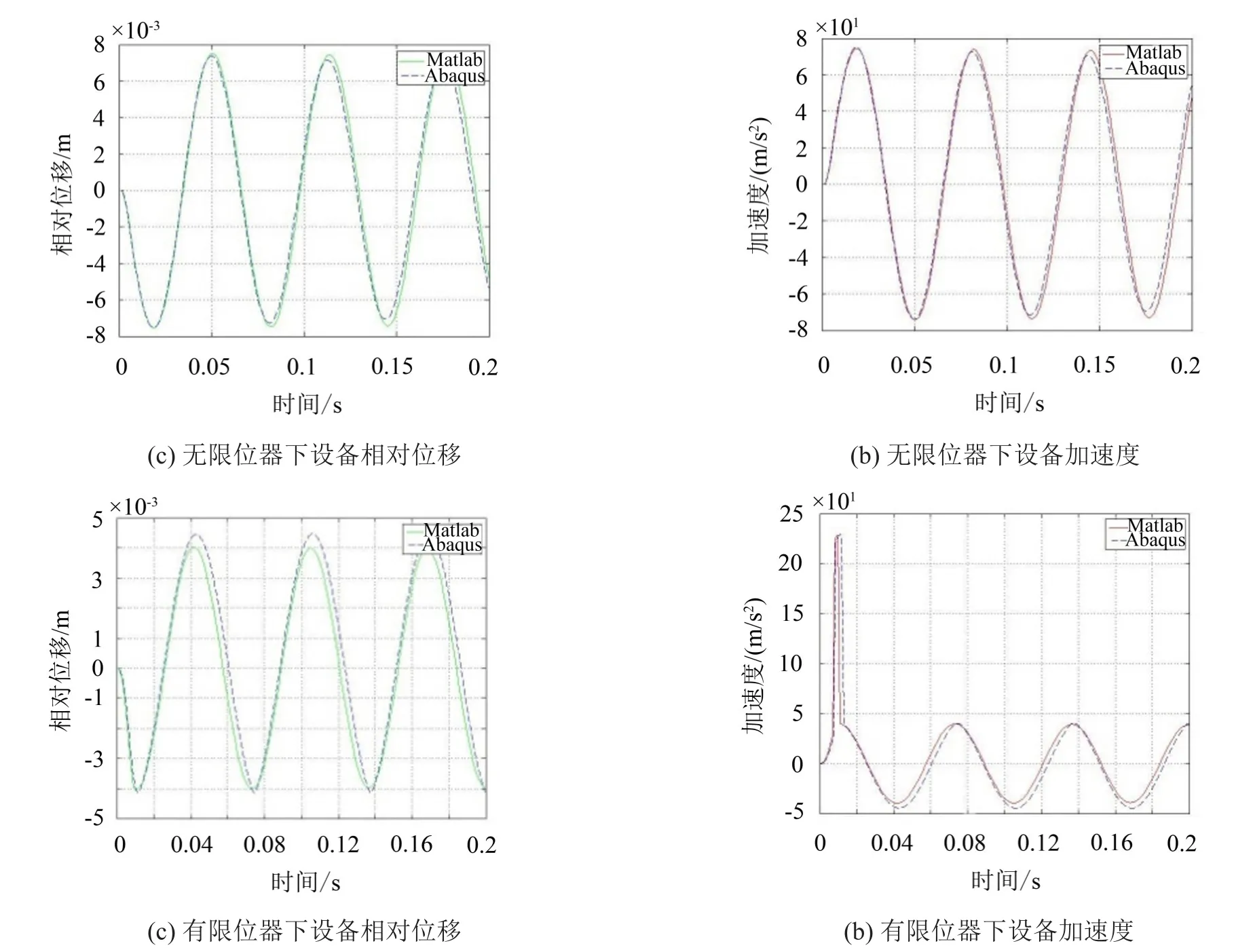
图5　Matlab与Abaqus对设备动力学仿真结果对比

由图5可知，对没有限位器的系统，有限元仿真得到的结果中设备的最大加速度为75 m/s2，设备的最大相对位移为7.49 mm；Matlab计算可得到设备的最大加速度为74.49 m/s2，设备的最大相对位移为7.54 mm。对有限位器的系统，设备的最大加速度为229.18 m/s2，设备的最大相对位移为4.13 mm；Matlab计算可得到设备的最大加速度为228.6 m/s2，设备的最大相对位移为4.05 mm，有限元仿真和Matlab理论解的结果高度吻合，其误差均小于2%。

3　实验结果与分析

3.1实验过程

该实验装置安装在CL-1000冲击跌落试验机的工作台面，通过KCL-2000电控仪操控。冲击测试仪器包括2个冲击加速度传感器、电荷放大器以及LMS数据采集分析仪。限位器材料采用相对密度为100的聚氨酯泡沫，其平台期应力α=65 290。为了加工方便，限位器采用正六面体结构，与设备接触的作用表面分别为60 mm×60 mm、80 mm×80 mm、100 mm×100 mm、120 mm×120 mm的正方形，工作间隙U0=5 mm。质量块质量为40 kg，隔振器选取型号为ZTA-18的弹簧隔振器，其刚度为9 500 N/m。

冲击实验测试方法：实验前将蓄电池冲击防护装置固定在冲击台台面，安装方式及承载方向均为竖直状态。安装2个加速度测量点：第一个在跌落式冲击机台面，第二个在质量块上端。实验中，通过控制柜控制冲击实验台台面上升高度，进行跌落实验。台面上升高度为75 mm～90 mm，高度依次递增，冲击输入脉宽约6 ms～10 ms。每次冲击实验后，通过数据采集系统同时测量和记录输入的冲击加速度信号与质量块的冲击加速度响应信号。

图6　冲击实验装置图

3.2实验结果分析

（1）同一限位器不同冲击高度下质量块加速度及相对位移对比

图7（a）为从75 mm、80 mm、85 mm、90 mm高度跌落后的输入加速度，其值从180 m/s2增加到386 m/s2。

图7（b）和（c）分别为无限位器时和100×100限位器作用下从各高度跌落后输入加速度和质量块加速度大小，表1为各工况下质量块响应情况。从表1中可以看出无限位器时，随着输入加速度的提高，质量块受到的冲击越来越大，加速度二次积分得到的相对位移也逐渐增加。在有限位器的情况下，与无限位器情况相比，虽然质量块与限位器的刚性接触造成了其加速度增大，但是质量块的相对位移有了大幅下降，避免了隔振器直接触底所造成更大的加速度破坏。

表1　实验结果　加速度/（m/s2）、位移/mm

图7　相同限位器下设备响应

（2）同一冲击高度不同限位器下质量块加速度及相对位移对比。

图8（a）和图8（b）为85 mm冲击高度下尺寸分别60×60、80×80、100×100、120×120的4种不同大小限位器作用下质量块的加速度和位移响应曲线，表2为其响应数值。可以看到，随着限位器作用面积的增大，质量块的加速度增大的越来越快，而相对位移逐渐减小，但是当限位器作用面积超过80×80后，质量块的相对位移下降幅度很小，说明此时限位器的作用面积不再是减少质量块相对位移的主要指标。

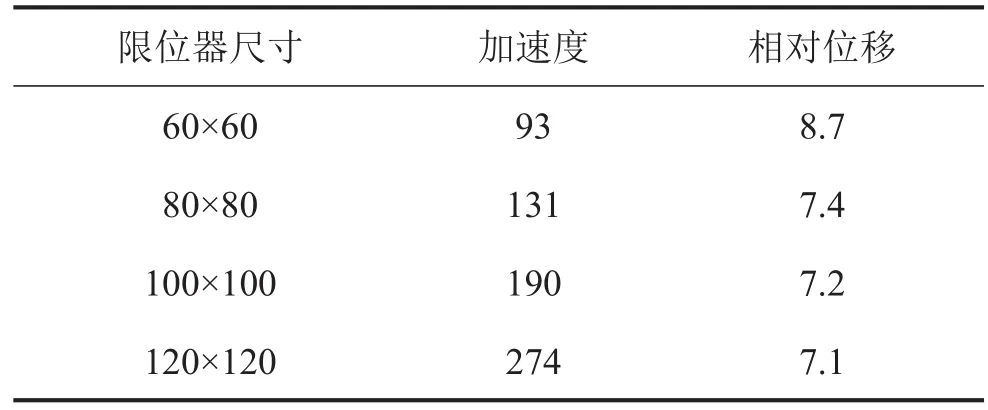
表2　实验结果 单位：加速度/（m/s2）、位移/mm

4　结语

本文提出采用聚氨酯泡沫作为限位器对设备进行限位，研究了舰船隔振装置中塑性限位器的设计方法，给出了塑性限位器的理论设计方法和设计计算流程。针对单层隔振装置计算模型，采用设计方法确定了塑性限位器参数。并采用Matlab对设备动力学响应进行仿真，弥补了Abaqus等有限元软件仿真计算时间过长的缺点，能够保证较高精度下快速得到相同条件下设备加速度和相对位移的时域响应曲线。

图8　相同冲击高度下设备响应

通过冲击高度及限位器大小两个维度进行一系列对比实验，实验结果符合预期，虽然结果的精确度达不到仿真的精度，这是由实验材料和理论模型的差距以及隔振器自身的局限性所导致的，但从实验效果来看，限位器的使用能改善在较高输入加速度情况下设备的相对位移，为塑性限位器的研究提供了新的思路和研究方法。

［1］孟庆国，杜俭业.国外舰艇抗冲击技术发展概况及启示［M］.北京：海潮出版社，2006，3-5.

［2］汪玉，华宏星.舰船现代冲击理论及应用［M］.北京：科学出版社，2005.

［3］SCAVUZZO R J，PUSEY H C.Naval shock analysis and design［M］.FallsChurch：TheShockandVibration InformationAnalysis Center，2000.

［4］刘建湖.舰船非接触水下爆炸动力学的理论与应用［D］.无锡：中国舰船科学研究中心博士论文，2002.

［5］LIN DAO-FU，YU YONG-FENG，HUA HONG-XING. The shock response analysis of a raft isolation system with restrictors［J］.Noise and Vibration Control，2004（1）：6-9.

［6］HANSSEN A G，LANGSETH M，HOPPERSTAD O S. Staticanddynamiccrushingofcircularaluminium extrusions with aluminium foam filler［J］.Int.J.Impact Engng，2000，24（5）：475-507.

［7］GIBSON L J，ASHBY M F.多孔固体结构与性能［M］.刘培生，译.北京：清华大学出版社，2003.

［8］赵应龙，何琳，黄映云，等.限位器对隔振系统抗冲击性能的影响［J］.振动与冲击，2005，24（2）：71-76.

［9］黄炼，吕志强，赵应龙，等.泡沫铝冲击吸能器应用设计［J］.舰船科学技术，2010（5）.

［10］SINGIRESU S RAO.机械振动［M］.李欣业，译.北京：清华大学出版社，2009.

［11］庄茁，由小川，廖剑晖，等.Abaqus的有限元分析和应用［M］.北京：清华大学出版社，2009.

［12］万松林，殷彩玉，焦素娟.塑性泡沫抗冲覆盖层深水爆炸响应分析［J］.噪声与振动控制，2015，35（6）：115-118.

［13］谢华，吴恒亮，车振东.聚氨酯弹性体隔振性能分析［J］.噪声与振动控制，2012，32（1）：154-156.

Design of Plastic Restrictor in a Single-stage Vibration Isolation System

HANYang，CHENYong，CHENFeng
（State Key Laboratory of Mechanical System and Vibration，Shanghai Jiaotong University，Shanghai 200240，China）

A strategy adopting polyurethane foam plastic restrictors to restrict the displacement of shipboard equipment in the single-stage vibration isolation system is proposed.The influence of parameters of the plastic restrictors on the maximum acceleration and maximum relative displacement of the shipboard equipment is studied.A theoretical method for determining the parameters of the restrictor is presented.Matlab code is used to quantify the plastic restrictor theory.The model of the single-stage vibration isolation system is designed and its computation program is done.Shock experiments are carried out to prove the correctness of the theory.

vibration and wave；polyurethane；restrictor；shock

V216.5

ADOI编码：10.3969/j.issn.1006-1335.2016.03.038

1006-1355（2016）03-0184-06

2015-12-08

韩阳（1991-），男，新疆乌鲁木齐市人，硕士生，主要研究方向为设备隔振抗冲研究。

谌勇，男，副研究员，博士生导师。E-mail：chenyong@sjtu.edu.cn