热镀锌线沉没辊动力学建模与稳定性分析
卢增静,肖 彪,李 伟,徐培民
热镀锌线沉没辊动力学建模与稳定性分析
卢增静,肖彪,李伟,徐培民
(安徽工业大学 机械工程学院,安徽 马鞍山 243032)
为弄清热镀锌线锌锅内沉没辊的振动机理,须对其进行动力学建模。对锌锅内组件进行适当简化,分析沉没辊运动和受力情况,建立仅包含部分段带钢、沉没辊和轴承力学模型。在力学模型基础上,利用达朗贝尔原理建立相应的非线性动力学方程。求出系统静平衡位置,得到系统相对于静平衡位置动力学方程。利用李雅普诺夫稳定性理论对沉没辊运动稳定性进行分析,得到稳定性判据。动力学模型建立为以后研究沉没辊振动响应和振动控制奠定了基础。由运动稳定性判据可知适当的初始张力、带速和校正辊上推量有利于沉没辊稳定运行。
振动与波;沉没辊;动力学模型;稳定性判据;达朗贝尔原理
在热镀锌生产线上,锌锅内辊子的振动会引起带钢的抖动,从而影响钢板镀锌质量。此外辊子旋转过程中,其两端的轴套与轴瓦相互接触摩擦,辊子的振动会加剧轴承的磨损,甚至使其失效。王军通过现场测试和有限元仿真分析,对沉没辊及其支架系统进行了模态分析[1]。李蛟龙建立了锌液和沉没辊流固耦合有限元模型,计算得到沉没辊在锌液中的模态,发现锌液中沉没辊的固有频率约为空气中的1/4[2]。王洋等利用广义Hamilton原理建立了出锌锅段带钢—辊子—柔性支承混杂系统的数学模型,并在静平衡位置对系统进行线性化,最后对该系统进行了模态分析[3]。李健等对锌锅区上行段进行动力学建模时将锌锅内辊子对带钢的影响用沿带钢横向的简谐激振力代替,得到了锌锅内辊子对带钢抖动影响较大的结论[4]。上述文献建模时均忽略了辊子两端滑动轴承的影响。
Younes研究了径向滑动轴承在半干摩擦状态下的动力学特性,分析了轴颈和轴瓦间的相互作用,并建立了轴颈沿切线方向的运动方程[5]。通过对状态方程线性化获得系数矩阵,最后利用Lyapunov理论判断系统的运动稳定性。陈锋等研究了润滑不良状态下轴承摩擦激励对螺旋桨推进轴系非线性振动特性的影响,基于拉格朗日方程和模态叠加法建立了系统非线性动力学方程,利用数值法求解系统响应[6]。研究结果表明,轴承摩擦负阻尼易引起系统摩擦自激振动。
本文从热镀锌线锌锅内结构的实际出发,考虑带钢弹性,忽略辊子及其吊臂的弹性,建立仅包含部分段带钢、沉没辊和轴承的振动模型,得到沉没辊非线性振动微分方程组。最后对系统运动稳定性进行分析。
1 沉没辊动力学建模
1.1锌锅内组件简化
热镀锌线锌锅内三个辊子均为被动辊,依靠两端轴套式滑动轴承支撑在辊架上,辊子随带钢轴向运动而转动。本文欲将工艺段带钢在校正辊和4号热张紧辊处截断,然后取这部分作为研究对象。由于沉没辊的最大工作转速nmax与第1阶临界转速nc之比nmax/nc<0.5,可将沉没辊假设为刚体[7]。当不考虑带钢的横向振动时,可忽略其弯曲刚度,将其简化为无质量的线性弹簧[8-9]。在忽略辊架弹性和振动的情况下,轴承可视为固定支承,辊架即为支承基础。用附加惯性来考虑锌液对辊子运动的影响。
为了建立简单而准确的力学模型,还应提出几点简化假设:
(1)不考虑辊子两端轴承的异动,即假设两端轴承同步运动,且不考虑辊子轴向运动,整个辊子的运动关于辊架对称面对称;
(2)轴颈与轴瓦间为干摩擦,且满足库伦摩擦定律;
(3)轴颈跟轴瓦始终接触;
(4)考虑带钢的张力波动;
(5)不考虑轴瓦和轴颈的磨损;
(6)辊子质量均匀分布;
(7)带钢在辊子上不打滑;
(8)带钢与辊子的接触切点不发生变化;
(9)忽略带钢跑偏以及翘曲变形。
1.2沉没辊力学模型
对沉没辊进行力学建模时要先弄清其运动和受力情况。沉没辊受到重力G,锌液浮力Ff,带钢张力Ti(i=1,2),两端轴承切向摩擦力Ft和摩擦力矩M(Ft),带钢与辊面间的静摩擦力矩M(Fs),以及辊架支反力FN的综合作用。
沉没辊的运动包括随带钢轴向运动的转动和沿着轴瓦内表面的涡动,其中辊子的转动又包括定轴匀速转动和转动振动两部分。
在忽略带钢跑偏以及翘曲变形的情况下,带钢、辊子和轴承存在一个纵向对称面,称之为“系统振动平面”,在该平面上建立沉没辊的力学模型,如图1所示。
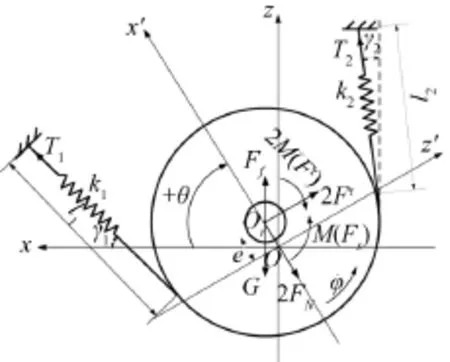
图1 沉没辊力学模型
引入固定坐标系Oxz,原点O为两端轴承中心连线与对称面的交点。辊子几何中心Or与坐标原点O的距离为e。ki(i=1,2)表示带钢的弹性。g1为4号热张紧辊至沉没辊段带钢与x轴的夹角,g2为校正辊上推量Dm给定时沉没辊至校正辊段带钢与z轴的夹角。辊子振动对g1和g2的影响较小,可忽略不计,则g1可作为确定的常数,g2与校正辊的上推量Dm有关。
沉没辊运转过程中任意时刻所处的位置可以用角位移j(t)和q(t)来表示,前者表示沉没辊绕其轴心的自转角位移,后者表示沉没辊中心绕固定坐标系原点O的涡动角位移。

式中q0为静平衡位置,Dq(t)代表相对于静平衡位置的涡动量,常数w0为与带钢运行速度对应的辊子名义角速度,Dj(t)为扭转振动角位移。
此处还需说明的是,从表面上看,图1所示力学模型中两处约束的表示方法似乎限制了带钢的轴向运动和辊子的转动。实际上,本文只是借用这种约束符号来表示4号热张紧辊和校正辊对轴向运动带钢的约束作用。
1.3沉没辊非线性动力学方程
在图2所示的力学模型的基础上,将沉没辊所受力系等效到质心Or处,根据D'Alembert原理,在点Or上虚加惯性力和力偶矩,如图2所示。
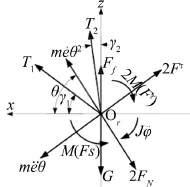
图2 沉没辊质心力系简图
根据力系平衡条件可得沉没辊的涡动和转动非线性动力学方程组,为了使系统更符合实际情况,加上阻尼得

式中m为沉没辊质量,J为其等效转动惯量,有效重力G'=G-Ff,R为沉没辊外半径,rj为轴颈半径,m为轴颈与轴瓦间的摩擦系数,c为黏性阻尼系数,其余参量见(1.2)节。
方程组(2)中张力Ti包括初始张力Ti0,沉没辊涡动引起的动张力DTi1,沉没辊扭转振动产生的动张力DTi2,因上游或下游系统动力学引起的动张力DTi3,而此部分动张力相当于外激励,则带钢总张力为

ki为第i段带钢的刚度系数,li0为第i段带钢初始长度,B为张力波动幅值,wb为张力波动频率,后两者的值来自现场的测试数据。
令系统的微分方程中对时间的导数项为零,波动张力DTij=0,可得到系统的静平衡方程。
沉没辊涡动静平衡方程为
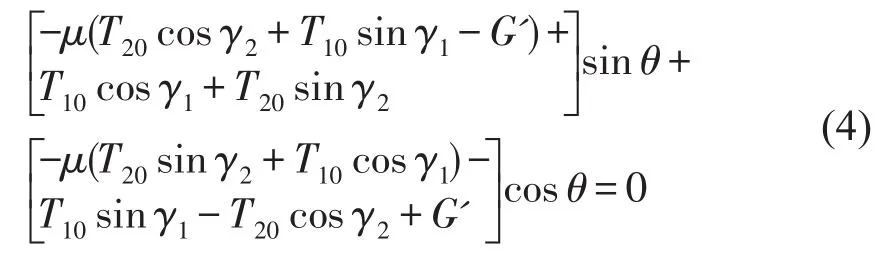
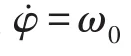

求解式(4)可得涡动静平衡点q0,将其代入式(5)可求得辊子转速w0。这说明,涡动静平衡点与系统构型、初始张力、校正辊上推量有关外,还与带速有关。
将平衡点q0代进(4)式和(5)式后,再将此二式代入方程组(2),即可得到沉没辊相对于平衡位置的非线性动力学方程组
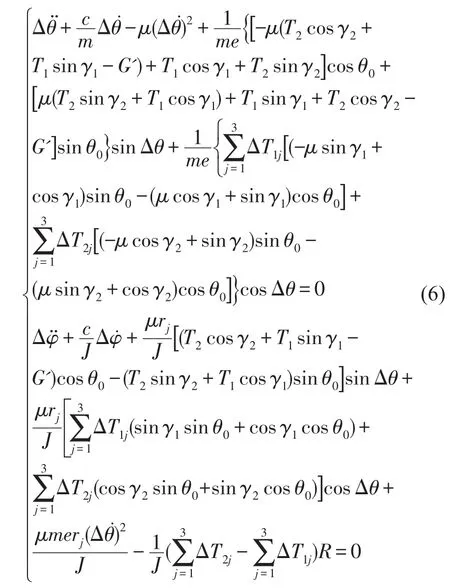
2 稳定性分析
本文是在不考虑动张力DTi3的情况下来分析沉没辊的运动稳定性,此时带钢总张力为

将式(7)代入方程组(6),将方程中sinDq和cosDq在Dq=0处泰勒级数展开,并保留方程组中Dq和Dj的二次以下项得
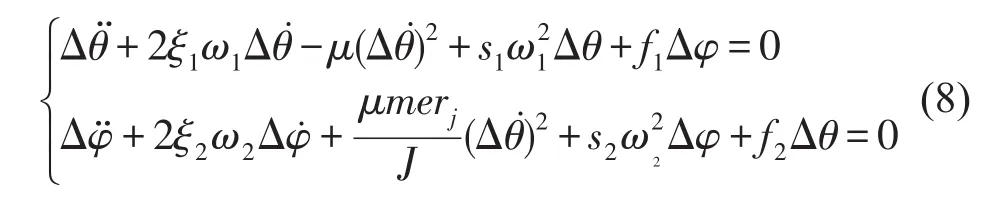

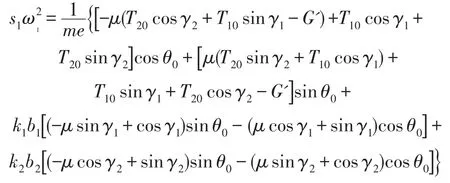
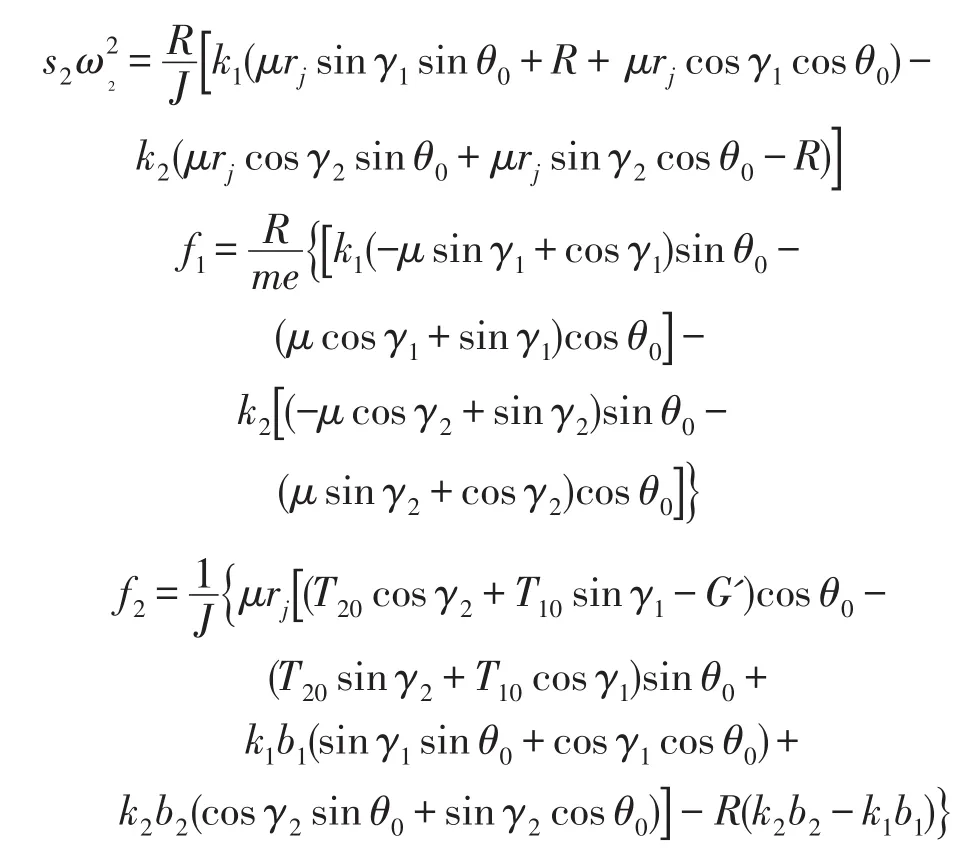
将式(8)表示在状态空间中,即可得到系统在状态空间的1阶运动微分方程组。

状态方程组式(9)的一次近似方程组为

1阶近似方程组式(10)在U1=U2=U3=U4=0处相对于变量U1、U2、U3、U4的雅克比矩阵为
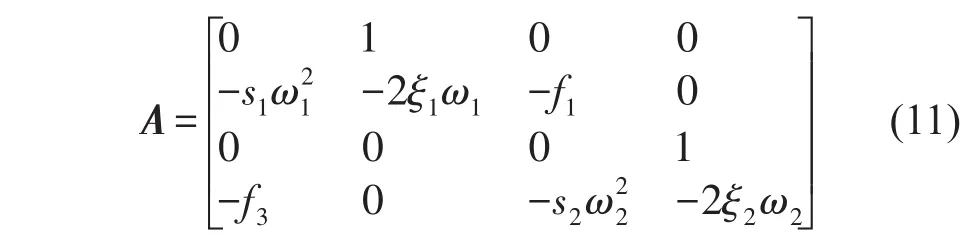
矩阵A对应的特征方程为

特征方程(12)的所有根具有负实部的充要条件为
(1)特征多项式的系数全部为正;
(2)一半Hurwitz(霍尔维茨)行列式大于零。
根据Lyapunov稳定性理论可知:若一次近似方程所有特征值的实部均为负,则原非线性方程的零解渐近稳定。由于微分方程未扰运动的稳定性等价于扰动微分方程零解的稳定性,则沉没辊运动稳定性判据为

当沉没辊的外形尺寸和带钢规格确定后,其相应的几何和物理参数可作为常数考虑。轴承半径间隙e,轴承处滑动摩擦系数m,带钢与辊面间静摩擦系数ms和带钢各段初始长度li0均为确定的常数。因此,沉没辊运动稳定性与带钢初始张力Ti0,校正辊上推量Dm和带速有关,生产实践中通过调节这些参数以满足不等式(12)即可使沉没辊稳定运行。
3 算例
以某热镀锌线为背景,带钢规格为1 mm×1 000 mm,取初始张力T20=32 000 N,带速v=90 m/s,阻尼比x1=x2=0.001,校正辊上推量Dm=30 mm,其它参数按实际情况取值,如表1所示。
根据表1中所列相关参数可计算出沉没辊的质量m=1 727 kg,有效重力G'=9 752 N,带钢的刚度系数k1=2.02×107,k2=4.20×108,参考文献[10-11]计算出有效转动惯量J=422 kg∙m2,根据欧拉公式可求得带钢初始张力T10=30 900 N。求解式(4)可得沉没辊涡动静平衡位置q0=1.10 rad。
将系统各相关参数和q0代入式(11),利用Matlab数值求解器计算出各特征值为

由于一次近似方程所有特征值的实部均为负数,则沉没辊的未扰运动是稳定的。
此外,由于上述系统参数能够满足不等式(12),亦可判断沉没辊的未扰运动是稳定的。
4 结语
利用D'Alembert原理建立了热镀锌线锌锅内沉没辊的动力学模型,该模型考虑了带钢弹性和沉没辊两端干摩擦滑动轴承的影响,比较真实地反映了实际情况。动力学模型的建立为以后研究系统响应,制定沉没辊振动的抑制策略奠定了基础。将Lyapunov稳定性理论与Hurwitz判据相结合得到了沉没辊运动稳定性判据,该判据为生产中调节带钢初始张力、带速和校正辊上推量以实现系统稳定运行提供了依据。

表1 系统几何和物理参数
[1]王军.热镀锌生产线出锌锅段带钢抖动现象动力学研究[D].合肥:安徽工业大学,2010.
[2]李蛟龙.冷轧带钢热镀锌沉没辊服役周期振动特性研究[D].武汉:武汉科技大学,2012.
[3]王洋,许飞,李勇,等.带钢-辊子-柔性支承混杂系统动力学建模与耦合振动研究[J].振动工程学报,2013,26(4):599-607.
[4]李健,颜云辉,郭星辉,等.基于薄板固有特性的连续热镀锌带钢表面质量在线控制[J].机械工程学报,2011,47(9):60-65.
[5]YOUNES Y K.On the dynamics and stability of a semidry journal bearing[J].Wear,1993(169):215-220.
[6]陈锋,张振果,张志谊,等.摩擦激励下螺旋桨推进轴系自激振动特性分析[J].噪声与振动控制,2015,35(2):117-120.
[7]钟一谔,何衍宗,王正,等.转子动力学[M].北京:清华大学出版社,1987:209-210.
[8]BEIKMANN R S.Static and dynamic behavior of serpentine belt drive systems:theory and experiment[D]. Michigan State:University of Michigan,1992.
[9]BEIKMANN R S.PERKINS N C.ULSOY A G.Design and analysis of automotive serpentine belt drive systems for steady state performance[J].Journal of Mechanical Design,1997,119(2):162-168.
[10]马斌捷,刘桢,林宏.航天器贮箱液体的有效转动惯量(上)[J].导弹与航天运载技术,2011(1):21-25.
[11]王基盛,杨庆山.流体环境中结构附加质量的计算[J].北方交通大学学报,2003,27(1):40-43.
Dynamic Modeling and StabilityAnalysis of the Sink Roll in a Hot-dip Galvanizing Line
LU Zeng-jing,XIAOBiao,LIWei,XU Pei-min
(School of Mechanical Engineering,Anhui University of Technology,Ma'anshan 243032,Anhui China)
In order to find out the vibration mechanism of the sink roll in hot-dip galvanizing lines,its dynamic model is established.The zinc pot hardware is appropriately simplified and the kinematic and dynamic perfoprmance of the sink roll is analyzed.A mechanical model including steel strip,sink roll and bearings is established.D'Alembert principle is used to derive the nonlinear dynamic equations.The system equilibrium positions are obtained according to the dynamic equations.Then,the new dynamic equations relative to the steady state of the system are derived.The stability analysis of the sink roll is performed by using Lyapunov stability theory,and the stability criterion is deduced.This dynamic model has provided the foundation for analyzing the vibration response and control measures for the sink rolls.Stability criterion demonstrates that the appropriate initial tension,strip velocity and roll engagement can increase the stability of the sink roll.
vibration and wave;sink roll;dynamic model;stability criterion;D'Alembert principle
TH113.1;O322
ADOI编码:10.3969/j.issn.1006-1335.2016.03.011
1006-1355(2016)03-0052-05
2015-12-30
卢增静(1990-),男,江苏省徐州市人,硕士研究生,主要研究方向为机械系统动力学与振动控制。E-mail:18895558100@163.com
徐培民,男,博士,教授。E-mail:xupeimin@ahut.edu.cn

