非均匀平面对称的Quintessence宇宙模型

王剑苹， 沈 明

(福州大学数学与计算机科学学院， 福建 福州　350116)



非均匀平面对称的Quintessence宇宙模型

王剑苹， 沈 明

(福州大学数学与计算机科学学院， 福建 福州350116)

构造一类特殊的非均匀平面对称度规， 利用理想流体的能动量张量， 在Quintessence模型的假设下求解Einstein场方程， 得到一类带有暗能量性质的非均匀平面对称宇宙模型. 此外， 通过计算模型的Hubble参数和减速因子等物理量， 分析了模型的物理性质.

Einstein场方程； 理想流体； 暗能量； Quintessence模型

0　引言

目前， 天文观测数据显示宇宙正在加速膨胀[1-2]. 加速膨胀现象表明宇宙中存在着暗能量， 暗能量被认为是导致宇宙加速膨胀现象的主要因素， 已成为当前研究热点[3-4]. Quintessence模型[5-6]是一种重要的暗能量模型. 结合Quintessence的状态方程， 并进一步拓展文献[7]中的度规以获得更具物理价值的Einstein场方程严格解[8-9]， 提出以下形式的非均匀平面对称度规：

(1)

其中:a是t的函数;b是t,x,y的函数. 通过求解， 获得三种形式的宇宙模型， 并利用Hubble参数和减速因子对模型的物理性质进行进一步的探索.

1　基本方程

Einstein场方程为

(2)

其中： Gij(i,j=0,1, 2, 3)为Einstein张量； Rij为Ricci曲率张量；R为标量曲率； Tij为能动量张量；κ是不改变所得空间性质的常数； gij为一个未知的洛伦兹度规， 即所需要求解的度规.

理想流体下的能量动量张量Tij由下式给出

(3)

其中:ρ表示理想流体的能量密度；p表示对应的压力； ui代表四维速度并满足

(4)

(5)

在随动坐标系下， 利用能动量张量(3)结合Einstein场方程(2)可得

(6)

(7)

(8)

(9)

(10)

(11)

(12)

由式(12)得到

(13)

通过方程(7)和(8)可得

(14)

将式(13)代入方程(14)有

(15)

其中: e(t)是t的函数.

因此， 可以得f(t， x)和g(t， y)的表达式

(16)

(17)

将式(13)代入方程(10)和(11)得

(18)

(19)

将式(16)和(17)代入式(18)和(19)， 则满足

(20)

即

(21)

由上可得

(22)

其中: c1， c2， c3为积分常数.

因此，

(23)

(24)

(25)

令r(t)=j(t)+n(t)， 则

(26)

观察方程(8)和(9)， 得方程

(27)

将式(26)代入式(27)， 得

(28)

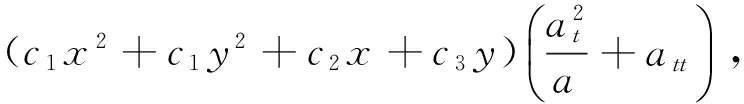
(29)

Quintessence暗能量的状态方程为

(30)

其中: w是w∈[-1， 0]的常数.

将式(30)代入式(6)和(9)得到

(31)

再将式(30)和式(26)代入方程(31)， 并通过移项得到方程

(32)

结合方程(29)， 最终得到方程组

(33)

由于b是x，y的函数， 即c1，c2，c3不全为0， 方程组(33)可转换为

(34)

2　方程的解

根据方程组(34)的特性， 将其分为三种情况分别进行讨论.

2.1w=0的情形

在w=0时， 通过求解方程组(34)的第二个方程， 可得

(35)

将式(35)代入方程组(34)的第一个和第二个方程得到

(36)

其中:a1，a2，a3，c1，c2，c3，r1，r2是积分常数. 在该情况下得到度规：

(37)

在此度规下， 通过方程(6)和(7)， 得到压强和能量密度分别为

(38)

(39)

2.2w=-1的情形

在w=-1时， 通过求解方程组(34), 得到a和b分别为

(40)

(41)

从而度规为

(42)

其中:a1，a2，a3，c1，c2，c3，r1是积分常数. 在此度规下， 得到压强和能量密度分别为

(43)

此时， 压强和能量密度都为常数， 即代表着宇宙是处于一种不变的状态.

2.3w≠-1且w≠0的情形

在w≠-1且w≠0时， 得到a和b为

(44)

(45)

其中:a1，a2，a3，c2，c3，r1是积分常数. 此时度规为

(46)

在此度规下， 将相应的a和b代入式(6)和(9)， 求得压强和能量密度分别为

(47)

(48)

此时度规场下的压强p<0且能量密度ρ>0， 显然符合暗能量模型. 由于该模型的能量密度ρ是关于时间t递减， 即意味宇宙随着时间的推进而膨胀， 并且当时间足够长时， 宇宙的压强和密度就会趋于零， 因此该模型与目前天文观测现象吻合. 并且此时经过验算， 模型的能量动量张量满足能量守恒定律.

观察度规(46)， 可得到平均标准尺度R(t)

(49)

计算Hubble值H和减速因子q， 分别为

(50)

(51)

3　结语

平面对称的时空是一类描述早期宇宙进化形态的重要模型， 对解释宇宙的进化过程有着重要意义. 在一类非均匀的平面对称度规下， 基于Quintessence的状态方程求解Einstein场方程， 得到三种满足能量守恒定律的暗能量宇宙模型， 并分析了其物理性质. 结果显示， 减速因子与状态方程参数有关， 当其取值为(-1， -1/3)时， 宇宙将加速膨胀.

[1] RIESS A G， FILIPPENKO A V， CHALLIS P，etal. Observational evidence from supernovae for an accelerating universe and a cosmological constant[J]. The Astronomical Journal， 1998， 116(3): 1 009-1 038.

[2] SPERGEL D N， BEAN R， DORE O，etal. Wilkinson microwave anisotropy probe (WMAP) three year results[J]. Implications for Cosmology， Astrophysical Journal Supplement Series， 2007， 170(2): 377-408.

[3] ELIZALDE E， NOJIRI S， ODINSTOV S D. Late-time cosmology in a (phantom) scalar-tensor theory: dark energy and the cosmic speed-up[J]. Physical Review D， 2004， 70(4): 636-640.

[4] MARINONI C， BUZZIL A. A geometric measure of dark energy with pairs of galaxies[J]. Nature， 2010， 468(7 323): 539-541.

[5] KATORE S D， ADHAV K S， SHAIKH A Y，etal. Plane symmetric cosmological models with perfect fluid and dark energy[J]. Astrophysics and Space Science， 2011， 333(1): 333-341.

[6] ZIMDAH W， PAVON D. Letter: statefinder parameters for interacting dark energy[J]. General Relativity and Gravitation， 2004， 36(6): 1 483-1 491.

[7] SHEN M， ZHAO L. Plane symmetric solutions to the Einstein’s field equations with dark energy[J]. Astrophysics and Space Science， 2012， 337(2): 753-757.

[8] KONG D X, LIU K L. Time-periodic solutions of the Einstein's field equations I: general framework[J]. Science in China Series A: Mathematics， 2010， 53(5): 1 213-1 230.

[9] STEPHANI H， KRAMER D. MACCALLUM M，etal. Exact solutions of Einstein’s field equations[M]. 2nd ed. Cambridge: Cambridge University Press， 2003.

(责任编辑： 洪江星)

Inhomogeneous plane symmetric cosmological models with Quintessence

WANG Jianping, SHEN Ming

(College of Mathematics and Computer Science, Fuzhou University, Fuzhou, Fujian 350116, China)

We construct an inhomogeneous plane symmetric metric, and solve the Einstein’s field equations in present of Quintessence with the energy momentum tensor of perfect fluid. We obtain the corresponding inhomogeneous plane symmetric cosmological models with dark energy. Moreover, the physical properties of the models with the Hubble parameter and the deceleration parameter are analyzed.

Einstein’s field equations； perfect fluid； dark energy； Quintessence model

10.7631/issn.1000-2243.2016.01.0012

1000-2243(2016)01-0012-05

2013-06-16

沈明(1983-)， 博士， 副教授， 主要从事几何物理中的偏微分方程的研究，shenming0516@fzu.edu.cn

国家自然科学青年基金资助项目(11101085)

O175.24

A