美国百年几何教科书中的棱柱定义

洪燕君，汪晓勤



美国百年几何教科书中的棱柱定义

洪燕君1，2，汪晓勤1

（1．华东师范大学数学系，上海 200241；2．石河子大学师范学院，新疆石河子 832000）

1829—1929年出版的70种美国中学几何教科书中先后给出了棱柱的6种定义，即欧几里得的定义、改进的欧氏定义、基于棱锥的定义、基于棱的定义、基于棱柱面的定义和基于棱柱空间的定义．尽管欧几里得的定义存在缺陷，但由于《几何原本》的深刻影响，该定义在很长时间里一直为教科书所广泛采用；直到19世纪末，才出现多种定义并存的现象，最终，棱柱面定义和改进的欧氏定义逐渐取代了旧定义．棱柱定义的百年演变反映了人们对棱柱概念由直观到严谨的认识过程，为今日教科书编写和课堂教学提供了一面镜子．

几何教科书；棱柱；欧几里得定义；棱柱面定义

棱柱是高中立体几何的重要概念之一，现行各版高中数学教科书所给出的棱柱定义互有不同．人教A版、沪教版、北师大版和湘教版给出了静态的定义，除了两个底面平行、全等外，关注棱柱侧面的属性；苏教版则给出动态定义，关注棱柱的形成过程．

教师在数学时，对一些概念和观点常会做出非正式的解释．从某种程度上讲，这种解释必须保持数学的精确性、逻辑性和规范性[1]．棱柱定义的教学实践表明，学生缺乏对数学知识的深刻理解和整体认识时[2]，很容易凭直觉形成“两个底面平行，侧面都是平行四边形的多面体叫棱柱”这一错误认识．那么，棱柱定义在历史上经历了怎样的演变过程？学生的错误认识是否具有历史相似性？棱柱定义的历史对研究者有何启示？在人教版高中数学教科书即将修订之际，研究者希望对上述问题作出回答．为此，研究者找到了1829—1929年间出版的70种美国几何教科书进行考察．为准确刻画出棱柱定义演变的历史脉络，对于同一作者再版的教科书，若内容无变化，则选取最早的版本；但若内容有变化，则将其视为不同教科书．

1 1829年以前的棱柱定义

在历史上，最早给出棱柱定义的是古希腊数学家欧几里得（Euclid，约公元前330—275年）．他在《几何原本》第11卷中定义棱柱如下：“一个棱柱是一个立体图形，它是由一些平面构成的，其中有两个面是相对的、相等的、相似的且平行的，其它各面均为平行四边形．”[3]虽然这个静态定义比较直观，但存在缺陷，因为存在满足定义条件、但并非棱柱的多面体．

18世纪，法国数学家瓦里格农（P. Varignon, 1654—1722）在其《数学基础》（1731）中摒弃了欧几里得的定义而采用了新的动态定义：“若平面直线形（如）按照平行于自身的方向从点移动到点，则该直线形画出一个界于两个相似且全等的图形和以及所有以图形的边为一边的平行四边形之间的立体．则该立体称为棱柱．”[4]如图1所示．

图1 瓦里格农的棱柱动态定义

之后，克莱罗（A. Clairaut, 1713—1765）在其《几何基础》（1741）中又回到欧氏定义上来：“两个底面为全等多边形，其余各个面均为平行四边形的立体．”[5]而勒让德（A. M. Legendre, 1752—1833）在《几何基础》（1794）中则对欧氏定义稍加改动：“棱柱是一个由若干平行四边形所围、两端为全等且平行的多边形的立体．”[6]勒让德的《几何基础》于1819年由哈佛大学数学教授法拉（J. Farrar, 1779—1853）译成英文，成为当时的美国大学几何教科书（在美国，直到1821年才出现今天意义上的中学）．1829年，英国数学家普雷菲尔（J. Playfair, 1748—1819）的英文版《几何原本》删节本在美国出版，书中完全照搬了欧氏定义[7]．

在棱柱定义上，除了瓦里格农的教材外，1829年以前的绝大多数教科书都打上了《几何原本》的烙印，也对美国早期教科书产生了深刻的影响．

2 百年几何教科书中的棱柱定义

70种几何教科书共计给出了71种棱柱定义，其中Baker（1893）的教科书给出了两种定义[8]．根据详尽的统计和分析，这些定义可分成“欧几里得的定义”、“改进的欧氏定义”、“基于棱锥的定义”、“基于棱的定义”、“基于棱柱面的定义”和“基于棱柱空间的定义”6类．没有出现瓦里格农的动态定义．

2.1 欧氏定义

研究者将用底面和侧面来描述的不完善的静态棱柱定义归为“欧氏定义”[9~50]，这类定义实质上与《几何原本》中的定义并无二致，其中，侧面只有“平行四边形”一个属性，而底面的属性互有不同，见表1．

表1 各种欧氏定义所涉及的底面属性

70种教科书中，只有两种教科书照搬了欧几里得的4个属性，见类型1；其他68种教科书都摒弃了“相似”这一多余属性．在这68种教科书中，只有3种明确保留了“相对”这一属性，见类型2；其它教科书都默认“相对”这一属性而不再提及，见类型3—9．

在侧面为平行四边形且具有平行公共边的条件下，对于底面属性的9种不同刻画本质上都是一致的．但在“侧面均平行四边形”的条件下，无论哪种刻画，都未能排除满足条件的反例．

2.2 改进的欧氏定义

“改进的欧氏定义”在欧氏定义的基础上，增加了侧面是平行四边形以外的其它属性，使得棱柱定义的完整性、严密性、规律性、有序性，有层次地展现出来[51]．所增加的属性有两类，一是侧面是平行四边形且有一组对边为两个底面的对应边．1876年，舒伊勒（A. Schuyler, 1828—1913）最早给出这类定义：“棱柱是一个多面体，它有两个面为全等、平行的多边形且对应边平行，其余各面均为以全等多边形对应边为底的平行四边形．”[52]

在Schuyler之后，Dodd & Chace（1898）、Sanders（1903）和Stone & Millis（1916）相继也给出了改进的欧氏定义[52~55]．其中，Stone & Millis（1916）的定义是：“棱柱是这样的多面体，它的两个面为平行平面上的全等多边形，其余各面均为平行四边形、且有一组对边分别为这两个全等多边形的对应边”，书中首次给出欧氏定义的反例，如图2所示．

图2 Stone & Millis的欧氏定义反例

改进的欧氏定义所增加的第二类侧面属性是“交线平行”．如Baker（1893）给出的定义是：“有两个相对的面为平行多边形，其余各面相交于平行线的多面体，称为棱柱．”[8]Hawkes，Luby & Touton（1922）的定义是：“棱柱是一个多面体，有两个面位于两个平行平面上，其余各面均为平行四边形，且其交线平行．”[56]这个定义与今日中国人教版和北师大版高中数学教科书中的定义一致．书中也给出了欧氏定义的反例，如图3所示．

图3 Hawkes等的欧氏定义反例

Thompson（1896）、Wells & Hart（1916）、Hawkes（1922）和Nyberg（1929）也给出了同类定义[56~59]．

2.3 基于棱锥的定义

只有两种教科书将棱柱视为特殊的棱锥．Dupuis（1893）给出的定义是：“当棱锥顶点沿垂直于底面的方向移动到无限远处，侧棱变成平行线，所得图形的平截体成了具有全等底面的封闭图形，称为棱柱．”[60]Baker（1893）给出的另一个定义是：“棱柱是一种特殊的棱锥，其顶点位于无限远处、侧棱相互平行．”[8]

虽然，将“棱柱”视为特殊的棱锥，不易为中学生所接受，但将两类几何体统一起来，对启发学生的思维、揭示不同数学对象之间的联系却是十分有意义的．这与将抛物线视为特殊的椭圆（有一个焦点位于无穷远处）是类似的．

2.4 基于棱的定义

教科书Bartol（1893）仅根据棱的特点来定义棱柱：“除了两个平行面截其余各面所得的棱以外，其他各棱都互相平行的多面体称为棱柱．”[61]这个定义是正确的，且有所创新．但根据欧拉公式，棱数等于面数与顶点数之和减去2，一个多面体的棱数一般比面数和顶点数多，故仅从棱的角度来看一个多面体，似乎增加了理解的难度．

2.5 基于棱柱面的定义

改进的欧氏定义需要罗列底面和侧面的各种属性，表述起来不简洁．因此，一些教科书编写者开始探讨新的更简洁的定义，于是，“基于棱柱面的定义”应运而生．这类定义又可分成4种情形．

第一种情形是采用一般棱柱面来定义棱柱．如：Keigwin（1897）给出的定义是：“棱柱是由棱柱面与两个平行截面所围成的多面体．”这是最早的“基于棱柱面的定义”[62]．作者将棱柱面定义为“由相交于平行线的平面所构成的图形”，并没有考虑棱柱面的封闭性，而用两个平行平面去截不封闭的棱柱面，并不能得到棱柱，因而相应的棱柱定义不够严谨．Phillips & Fisher（1898）和Hart & Feldman（1912）也采用了类似的定义[63~64]，前者将棱柱面定义为“由依次过一组平行线中的两条平行线的平面构成的面”，后者将棱柱面定义为“始终与一条固定折线相交，且保持与一条固定直线（与折线不共面）平行的动直线所形成的面”，两者都没有考虑棱柱面的封闭性．由此可见，棱柱面的定义也经历了从静态到动态的过程．

第二种情形是不定义棱柱面，而直接用“相交于平行线的一组平面”来代替棱柱面．如Durell（1909）、Shutts（1912）和Durell & Arnold（1917）都将棱柱定义为：“由两个平行平面和一组相交于平行线的平面所围成的多面体．”[65~67]这种定义与第一种情形等价．

第三种情形是采用封闭棱柱面来定义棱柱．Slaught & Lennes（1911）先定义“封闭棱柱面”：“给定一个凸多边形和一条与该多边形不共面的直线．若直线沿多边形运动一周，直线始终与自身平行且与多边形的边界相交，则称直线所生成的面为封闭棱柱面．”再定义棱柱：“封闭棱柱面界于两个平行横截面之间的部分，连同两个横截面，称为棱柱．”[68]这个定义关注棱柱的表面，无法定义棱柱体积，因而有些瑕疵．事实上，该教科书的修订版（Slaught & Lennes，1919）对棱柱定义进行了明显的改进：“由棱柱面和两个与所有母线都相交的平行横截面所围成的多面体称为棱柱．”[69]

Betz & Webb（1916）、Palmer & Taylor（1918）和Sykes & Comstock （1922）都给出了类似的定义[70~72]：“一个封闭棱柱面被两个平行平面所截，所形成的立体称为棱柱．”

第四种情形是缩小棱柱面概念的外延，将其等同于封闭棱柱面．Schultze & Sevenoak（1922）将棱柱面定义为：“始终与给定多边形的边界相交、且平行于不在多边形所在平面上的固定直线的一条动直线所形成的面称为棱柱面．”相应地，将棱柱定义为：“由棱柱面与两个平行平面所围成的多面体．”[73]

引入“封闭棱柱面”概念，或将棱柱面概念特殊化（准线为多边形），都完善了基于一般棱柱面的棱柱定义．

2.6 基于棱柱空间的定义

Edwards（1895）最早将棱柱定义为“任意多个相交于平行线的平面与两个平行平面所围的部分空间”[74]，但并没有给出“棱柱空间”概念．

Beman & Smith（1900）最早给出棱柱空间的定义[75]．他们先定义棱柱面：“由相交于平行线的部分平面所构成的面称为棱柱面”，再定义棱柱空间：“若从棱柱面的某一平面开始，每一个平面与下一个平面相交，最后一个平面与第一个平面相交，则称棱柱面围成一个棱柱空间．”最后再定义棱柱：“棱柱空间界于两个平行横截面之间的部分称为棱柱．”Smith（1913）和Richardson（1914）沿用了这个定义[76~77]．但后者对棱柱面和空间给出了更清晰的数学表述：

“个平面1，2，…m（其中任何3个不共线）依次相交于平行线，则这个平面位于平行线之间的各部分构成棱柱面．若最后一个平面m又与第一个平面1相交，则称棱柱面围成了一个棱柱空间．”

3 棱柱定义的演变

可以用时间轴来表示棱柱定义的历史发展进程，如图4所示．从图中可见，从欧几里得到舒伊勒，棱柱的静态定义从不完善到完善，走过了两千一百多年的漫长岁月；而从欧氏完善定义的诞生，到该定义的反例的出现，匆匆又过了40年！由于《几何原本》的影响、欧几里得的权威性以及欧氏定义的直观性，后世教科书编写者采取了全盘照搬的方式，丝毫不曾怀疑棱柱定义存在缺陷，因而使得该定义谬种流传，甚至在出版于1948年的美国几何教科书中，仍能看到欧氏定义．在基于一般棱柱面的定义和基于封闭棱柱面的定义之间，也间隔了整整14年．

图5给出了6种定义的频数分布情况，从中可见，欧氏定义出现的频数遥遥领先，而基于棱柱面的定义位居第二．

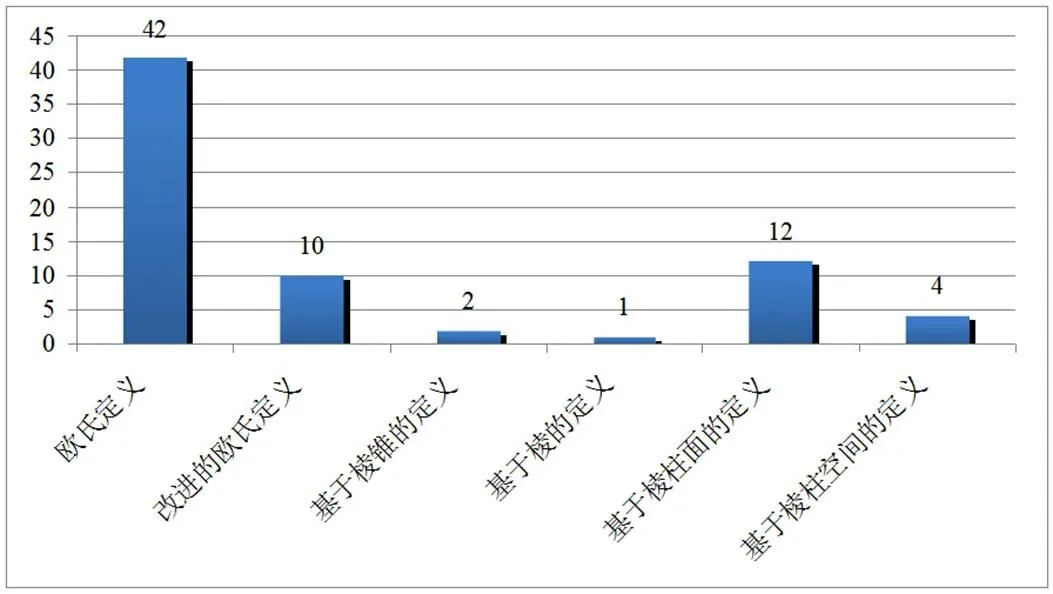
图5 各类定义的总体频数分布

研究者将一百年时间分成5段，各类定义在各段时间的分布如图6．从图6可见，前60年，欧氏定义一统天下．到了后40年，才出现多元化的局面，直到最后20年，欧氏定义一枝独秀的局面才发生了彻底改变．

改进的欧氏棱柱定义于1876年诞生之后，完善的定义与不完善的定义依然交替出现，这一方面说明，由于舒伊勒没有给出欧氏定义的反例，导致后来的教科书编写者未能意识到欧氏定义与改进的欧氏定义之间的区别；另一方面也说明，要动摇欧氏的权威，改变人们心中根深蒂固的概念意象是多么地艰难．无疑，棱柱定义的完善过程中，能否找到欧氏定义的反例至关重要．1916年，Stone和Millis在其教科书中给出反例之后，欧氏定义的权威被彻底颠覆，于是，才看到了棱柱面定义后来居上的局面．随着棱柱面定义的出现，棱柱的正确定义在数量和形式上都逐步显呈上升态势．

图6 各类定义在不同时间段的分布情况

4 结论与教学启示

跨越百年的70种美国早期几何教科书清晰地展现了棱柱定义的历史发展脉络．在半个多世纪里，欧几里得的不完善定义占有绝对统治地位，《几何原本》的权威性以及几何知识结构的思考单一化，导致新定义的姗姗来迟．而在改进的欧氏定义诞生之初，并没有伴随旧定义反例的出现，人们因此忽视新旧定义之间的差异，使得欧氏定义在相当长的时间内依然扮演主角．只有当反例出现之后，人们才逐渐摒弃欧氏定义，棱柱定义趋于多元化，最终，基于棱柱面的定义占据上风．而基于棱柱面的定义又经历了从一般棱柱面到封闭棱柱面的过程，最终才臻于完善．此外，从棱柱面定义又衍生出棱柱空间的定义，这种定义同样经历从不完善到完善的过程．

棱柱定义的历史也为今日课堂教学和教科书编写带来了诸多启示．

（1）对教科书编写者的启示．

18世纪，瓦里格农已经给出了正确的动态定义．但由于他的《数学基础》没有传入美国，因而所考察的美国百年教科书中，没有一种教科书采用这种定义，棱柱的错误定义不断被重复．因此，教科书编写者首先需要有国际视野，广泛阅读、深入研究国外同类教科书，扬长避短，为自己的教科书服务．其次，他们也需要有批判的精神，不能盲目地迷信权威、全盘照搬．再次，教科书编写者也需要有历史感．棱柱定义的历史表明，静态定义绵延不绝而动态定义则无人问津，基于棱柱面的定义后来居上，而基于棱或棱锥的定义则昙花一现．据此可以做出最佳选择．

（2）对课堂教学的启示．

首先，可以借鉴棱柱定义从不完善到完善的演变过程，运用重构历史的方式来设计棱柱概念的教学．通过多媒体技术，演示平面旋转立体图形过程，培养学生的动态观[78]，并让学生从实物中归纳棱柱的共同特征，在此基础上给棱柱下定义；通过反例来修正、完善定义，让学生经历棱柱概念的形成过程，加深让学生对棱柱概念的理解．在这个过程中，老教师要重视与学生的互动，而新教师则更要注重学生的自主参与、学生练习[79]．同时，运用附加历史的方式，在课堂上向学生介绍欧氏定义，让他们了解历史上的数学家也犯过错误，从而正确认识数学活动的本质，树立数学学习的自信心．

其次，可以将棱柱的历史加工为教学素材．在教学中，可以通过复制或顺应的方式，将改进的欧氏定义或其他定义在历史上的不同表述形式呈现给学生，让他们运用立体几何知识来辨析正误、论证异同，加速知识点的完备化进程．

［参考文献］

[1] 张奠宙，戴再平．中国数学教学中的“双基”和开放问题解决[J]．数学教育学报，2005，14（4）：1-8．

[2] 苏红雨，江雪萍．基于几何问题情境的高中教师的数学素养研究[J]．数学教育学报，2010，19（1）：81-85．

[3] 欧几里得．几何原本[M]．兰纪正，朱恩宽译．西安：陕西科技出版社，2003．

[4] Varignon P.[M]. Amsterdam: Francois Changuion, 1731.

[5] Clairaut A.[M]. Paris: Durand, 1741.

[6] Legendre A M.[M]. Cambridge, N. E.: The University Press, 1794.

[7] Playfair J.[M]. Philadelphia: A. Walker, 1829.

[8] Baker A L.[M]. Boston: Ginn and Company, 1893.

[9] Perkins G R.[M]. New York: D. Appleton & Company. 1850.

[10]  Sharpless I.[M]. Philadelphia: Porter & Coates, 1879.

[11]  Hayward J.[M]. Cambridge: Hilliard & Brown, 1829.

[12]  Robbins E R.[M]. New York: American Book Company, 1907.

[13]  Robbins E R.[M]. New York: American Book Company. 1916.

[14]  Robinson H N.[M]. Cincinnati: Jacob Ernst, 1850.

[15]  Robinson H N.[M]. New York: Ivison, Blakeman, Taylor & Company, 1868.

[16]  Wells W.[M]. Boston: Leach, Shewell & Sanborn, 1886.

[17]  Milne W J.[M]. New York: American Book Company, 1899.

[18]  Wells W.[M]. Boston: D. C. Heath & Company, 1908.

[19]  Walker T.[M]. Boston: Richardson & Lord, 1829.

[20]  Peirce B.[M]. Boston: James Munroe & Company, 1837.

[21]  Loomis E.[M]. New York: Harper & Brothers, 1849.

[22]  Perkins G R.[M]. New York: D. Appleton & Company, 1855.

[23]  Benjamin G.[M]. Boston: Robert S. Davis & Company, 1859.

[24]  Evans E W.[M]. Cincinnati: Wilson, Hinkle & Company, 1862.

[25]  Tappan E T.[M]. Cincinnati: Sargent, Wilson & Hinkle, 1864.

[26]  Wentworth G A.[M]. Boston: Ginn & Heath, 1880.

[27]  Wentworth G A.[M]. Boston: Ginn & Heath, 1881.

[28]  Newcomb S.[M]. New York: Henry Holt & Company, 1884.

[29]  Bayma J.[M]. San Francisco: A. Waldteufel, 1885.

[30]  Halsted G B.[M]. New York: John Wiley and Sons, 1885.

[31]  Tappan E T.[M]. New York: D. Appleton & Company, 1885.

[32]  Newcomb S.[M]. New York: Henry Holt & Company, 1889.

[33]  Bowser E A.[M]. New York: D. van Nostrand Company, 1890.

[34]   van Velzer C A, Shutts G C.[M]. Chicago: Atkinson, Mentzer & Grover, 1894.

[35]  Hull G W.[M]. Philadelphia: Butler, Sheldon & Company, 1897.

[36]  Gore J H.[M]. New York: Longmans, Green and Company, 1899.

[37]  Wentworth G A.[M]. Boston: Ginn & Company, 1899.

[38]  Shutts G C.[M]. Chicago: Atkinson, Mentzer & Grover, 1905.

[39]  Failor I N.[M]. New York: The Century Company, 1906.

[40]  Schultze A, Sevenoak F L.[M]. New York: The Macmillan Company, 1908.

[41]  Keller S S.[M]. New York: D. van Nostrand Company, 1908.

[42]  Wentworth G A, Smith D E.[M]. Boston: Ginn & Company, 1911.

[43]  Ford W B, Ammerman C.[M]. New York: The Macmillan Company, 1913.

[44]  Bruce W H, Cody C C.[M]. Dallas: The Southern Publishing Company, 1914.

[45]  Williams J H, Williams K P.[M]. Chicago: Lyons & Carnahan, 1916.

[46]  Newell M J, Harper G A.[M]. Chicago: Row, Peterson & Company, 1918.

[47]  Macnie J.[M]. New York: American Book Company. 1895.

[48]  Stewart S T.[M]. New York: American Book Company, 1891.

[49]  Davies C.[M]. Philadelphia: A. S. Barnes & Company, 1841.

[50]  Bush W N, Clarke J B.[M]. New York: Silver, Burdett & Company, 1905.

[51] 谢汉民．立几教学中的简洁美管见[J]．数学教育学报．1995，4（4）：76-77．

[52]  Schuyler A.[M]. Cincinnati: Wilson, Hinkle & Company, 1876.

[53]  Dodd A A, Chace B T.[M]. Kansas City: Hudson-Kimberly Publishing Company, 1898.

[54]  Sanders A.[M]. New York: American Book Company, 1903.

[55]  Stone J C, Millis J F.[M]. Chicago: B. H. Sanborn & Company, 1916.

[56]  Hawkes H E, Luby W A, Touton F C.[M]. Boston: Ginn & Company, 1922.

[57]  Thompson H D.[M]. New York: The Macmillan Company, 1896.

[58]  Wells W, Hart W W.[M]. Boston: D. C. Heath & Company, 1916.

[59]  Nyberg J A.[M]. New York: American Book Company, 1929.

[60]  Dupuis N F.[M]. New York: Macmillan & Company, 1893.

[61]  Bartol W C.[M]. Boston: Leach, Shewell, and Sanborn, 1893.

[62]  Keigwin H W.[M]. New York: Henry Holt & Company, 1897.

[63]  Phillips A W, Fisher I.[M]. New York: American Book Company, 1898.

[64]  Hart C A, Feldman D D.[M]. New York: American Book Company, 1912.

[65]  Durell F.[M]. New York: Charles E. Merrill Company, 1909.

[66]  Shutts G C.[M]. Boston: Atkinson, Mentzer & Company, 1912.

[67]  Durell F, Arnold E E.[M]. New York: Charles E. Merrill Company, 1917.

[68]  Slaught H E, Lennes N J.[M]. Boston: Allyn and Bacon, 1911.

[69]  Slaught H E, Lennes N J.[M]. Boston: Allyn and Bacon, 1919.

[70]  Betz W, Webb H E.[M]. Boston: Ginn & Company, 1916.

[71]  Palmer C I, Taylor D P.[M]. Chicago: Scott, Forsman & Company, 1918.

[72]  Sykes M, Comstock C E.[M]. Chicago: Rank Mcnally & Company, 1922.

[73]  Schultze A, Sevenoak F L.[M]. New York: The Macmillan Company, 1922.

[74]  Edwards G C.[M]. New York: Macmillan & Company, 1895.

[75]  Beman W W, Smith D E.[M]. Boston: Ginn & Company, 1900.

[76]  Smith E R.[M]. New York: American Book Company, 1913.

[77]  Richardson S F.[M]. Boston: Ginn & Company, 1914.

[78] 黄继蓉，陈光喜．多媒体技术与数学“数形结合”教学[J]．数学教育学报，2009，18（2）：76-78．

[79] 斯海霞，叶立军．新老教师数学抽象概括教学差异的比较研究[J]．数学教育学报，2010，19（6）：53-55．

[责任编校：周学智]

Definitions of the Prism in Geometry Textbooks from 1829 to 1929

HONG Yan-jun1, 2, WANG Xiao-qin1

(1. Department of Mathematics, East China Normal University, Shanghai 200241, China;2. Normal College, Shihezi University, Xinjiang Shihezi 832000, China)

This paper analyzes the prism definitions in 70 US geometry textbooks from 1829 to 1929, namely, Euclid’s definition, improved Euclidean definition, definitions based on the pyramid, the edge, the prismatic surface and the prismatic space. Due to the far-reaching impact of The Elements, the Euclid’s definition, though not perfect, had remained in textbooks for a long time. Not until the end of 19 century, did a variety of definitions coexist. In the end, the improved Euclidean definition and the definition based on the prismatic surface took the place of the old ones. The history of prism definition reveals that our understanding on prism has experienced a gradual process, from intuitive to rigorous, which might provide some inspiration for today’s prism teaching.

geometry textbook; prism; Euclidean definition; the definition based on the prismatic surface

G40-059.3

A

1004–9894（2016）05–0067–06

2016–04–10

人教社课程与教材研究所“十二五”规划课题——数学史融入数学教材研究（KC2014—010）

洪燕君（1972—），女，四川富顺人，石河子大学副教授，华东师范大学数学系博士研究生，主要从事数学史与数学教育研究．