与分担函数相关的正规定则

杨端阳，叶亚盛

（上海理工大学理学院，上海200093）

与分担函数相关的正规定则

杨端阳，叶亚盛

（上海理工大学理学院，上海200093）

本文研究了与分担函数相关的亚纯函数族的正规性的问题.利用Nevanlinna理论的方法，得到了一个正规定则，推广了庞学诚和Zalcman［3］的一个结果.

正规族；分担值；分担函数；亚纯函数

1　引言

设区域D为复平面C上的一个区域，F是区域D内的亚纯函数族.若对于F中任一函数序列均可选出一个子序列在区域D上按球距内闭一致收敛，则称F在区域D内正规.设f（z）和g（z）是区域D内的两个亚纯函数，a和b是两个复数，若当f（z）=a，有g（z）=b，记f（z）=a⇒g（z）=b.若f（z）=a⇒g（z）=b和g（z）=b⇒f（z）=a，记f（z）=a⇔g（z）=b.若f（z）=a⇔g（z）=a.则称f（z）和g（z）是区域D上IM分担a.

1979年，顾永兴证明了Hayman关于正规族的猜想，得到如下著名的正规定则.

定理A［1］设F是区域D内的亚纯函数族，k是一个正整数.若对于F中的每一个函数f，有f（z）/=0，f（k）（z）/=1.则F在区域D内正规.

1986年，杨乐改进了定理A的结果，得到

定理B［2］设F是区域D内的亚纯函数族，k是一个正整数，h（z）（/≡0）是区域D内的全纯函数.若对于任意的f∈F，f（z）/=0，f（k）（z）/=h（z），则F在区域D内正规.

2002年，庞学诚和Zalcman考虑涉及零点重级的亚纯函数的情况，证明了

定理C［3］设k是一个正整数，h（z）（/≡0）是区域D内的全纯函数，F是区域D内的亚纯函数族，其零点重级均至少为k+3.若对于任意的f∈F，f（k）（z）/=h（z），则F在区域D内正规.

推广定理C，得到如下结果

定理1设k是一个正整数，M是正数，h（z）（/≡0）是区域D内的全纯函数，F是区域D内的亚纯函数族，其零点重级均至少为k+3.若对于任意f∈F，f（k）（z）h（z）⇒|f（z）|≥M，则F在区域D内正规.

例1设D=z：|z|≤1，h（z）=z，F=｛fn（z）｝，其中.当时，|fn（z）|=0.然而F在区域D内不正规，这是因为当n→∞时，→∞，fn（0）=0.

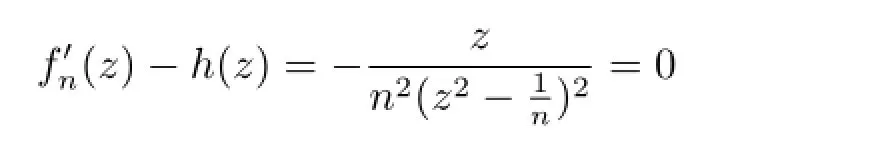
例1说明f（k）（zh（z）⇒|f（z）|≥M是个必要条件.

在文献［3］中的例1说明零点重级均至少为k+3也是必要的.

定理2设k是一个正整数，h（z）（/≡0，∞）是区域D内的亚纯函数，其极点的重级均之多为k-1，F是区域D内的亚纯函数族，其零点重级均至少为k+3.若对于任意的f∈F， f（k）（z）h（z）⇒|f（z）|≥M，则F在区域D内正规.

2　相关引理

为了证明定理，需要下面的引理

引理2.1［4］设k是一个正整数，F是单位圆盘上的亚纯函数族，其零点重级至少为k，且存在A≥1，使得对于任意f，在f零点处，都有|f（k）（z）|≤A.假设F在z0处不正规，则对0≤α≤k任意，必存在

a.点列zn，zn→z0；

b.函数列fn∈F；

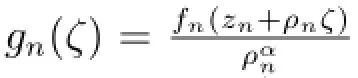
引理2.2［5］设k是一个正整数，f（z）是超越亚纯函数，R（z）（/≡0）是有理函数.若除有限个点外，f（z）的零点重级至少为k+2，那么f（k）（z）-R（z）有无穷多个零点.

引理2.3［6］设k是一个正整数，f（z）是有穷级亚纯函数，其零点重级均至少为k+2.若f（k）（z）/=1，则f（z）是常数.

引理2.4［3］设f（z）是非常数有理函数，k，m是正整数.若f（z）的零点重级均至少为k+3，则对于任意正整数m，在复平面上f（k）（z）=zm有解.

引理2.5［7］设F是单位圆盘上的亚纯函数族，a是一个有穷复数或∞，且每个任意f∈F，f/=a.若F在△＇内正规，在z=0处不正规，则存在F的子列fn，使得fn→a在△＇内.

引理2.6［8］设k，m是一个正整数，f（z）是有理函数，其零点的重级均至少为k.如果f（k）（z）/=z-m，那么f（z）是常数.

引理2.7设｛fn（z）｝是区域D内的亚纯函数列，其零点重级均至少为k+3，｛hn（z）｝是区域D内的全纯函数列，并且一致收敛于全纯函数h（z）（/=0）.若对于任意正整数n，=hn（z）⇒|hn（z）|≥M，则｛fn（z）｝在区域D内正规.

证设z0为D内任意一点，下证｛fn（z）｝在z0处正规.由于h（z）/=0，不妨设h（z0）=1.假设｛fn（z）｝在z0处不正规，由引理2.1，存在点列zn，zn→z0，｛fn（z）｝的子列（仍记为｛fn（z）｝），正数列ρn→0，使得在复平面C上按球距内闭一致收敛于非常数亚纯函数g（ζ），其零点重级至少为k+3，级至多为2.

断言：g（k）（ζ）/=1.

若不然，存在ζ0，使得g（k）（ζ0）=1.显然g（k）/≡1.否则，g（ζ）是次数为k的多项式，这与g（ζ）的零点重级至少为k+3矛盾.又因为（zn+ρnζ）-hn（zn+ρnζ）=-hn（zn+ρnζ）→g（k）（ζ）-1，由Hurwitz定理，存在ζn，ζn→ζ0，使得当n充分大时，（zn+ρnζn）=hn（zn+ρnζn），根据条件可得|fn（zn+ρnζn）|≥M，则

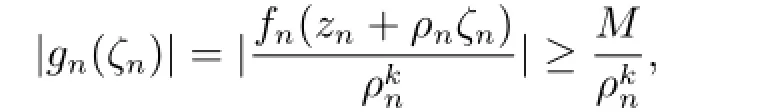
由于g（ζ）的零点重级至少为k+3，由引理2.3，g（ζ）是常数，矛盾.

3　定理的证明

定理1的证明不妨设D为△，z0为△内任意一点.下证F在z0处正规.下面分两种情况讨论.

情形1 h（z0）/=0，则存在δ＞0，使得在△（z0，δ）内，h（z）/=0.由引理2.7，F在z0处正规.

情形2 h（z0）=0.不失一般性，令z0=0，h（z）=zmφ（z），其中在△内φ（0）=1，φ（z）/= 0.由情形1，F在△＇=△｛0｝内正规，下证F在z0=0处正规.

令F∞：｛F（z）=，f∈F｝.显然f（0）/=0.否则，f（0）=0.由于f零点重级均至少为k+3，则f（k）（0）=0，即f（k）（0）=h（0），根据条件0=|f（0）|≥M，矛盾.由于f（0）/=0，则F（0）=∞.下证F∞在z0=0处正规.

假设F∞在z0=0处不正规，由引理2.1，存在点列zn，zn→0，函数列Fn∈F∞，正数列ρn→0+，使得

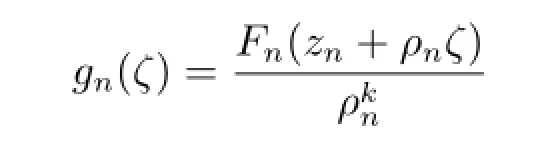
在复平面C上按球距内闭一致收敛于非常数亚纯函数g（ζ），其零点重级至少为k+3，级至多为2.

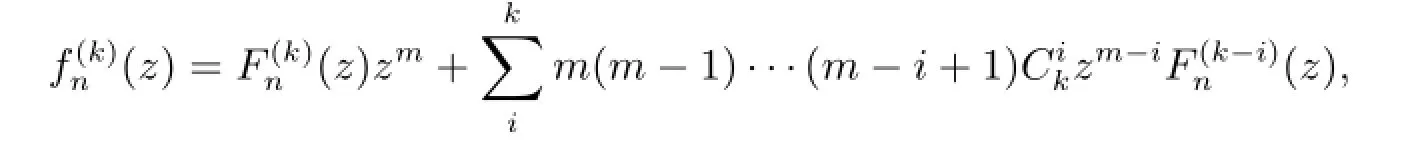
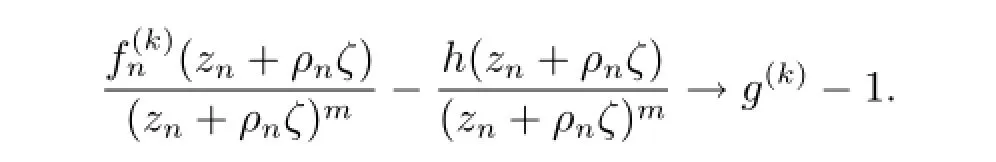
断言：g（k）（ζ）/=1.

若不然，存在ζ0，使得g（k）（ζ0）=1.显然，g（k）（ζ）/=1.否则，g（ζ）是次数为k的多项式，这与g（ζ）的零点重级至少为k+3矛盾.由Hurwitz定理，存在ζn，ζn→ζ0，使得当n充分大时，（zn+ρnζn）=h（zn+ρnζn）.根据条件可得|fn（zn+ρnζ）|≥M，则

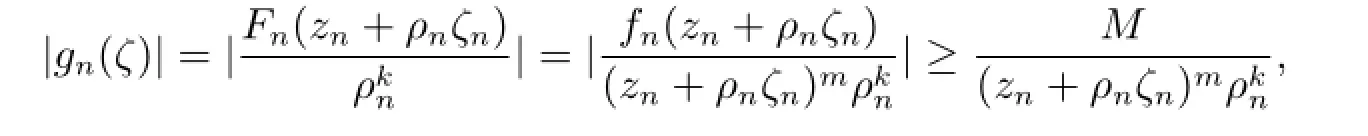
由于g（ζ）的零点重级至少为k+3，由引理2.3，g（ζ）是常数，矛盾.

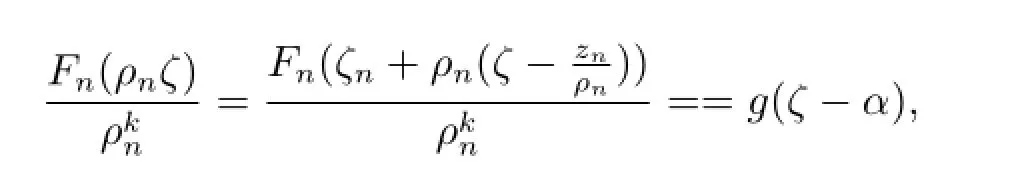
所以g（ζ-α）的零点重级至少为k+3，并且0是g（ζ-α）的重级至少为m的极点.

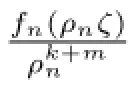
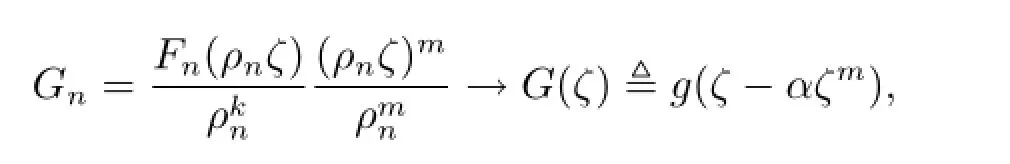
其中G（ζ）的零点重级至少为k+3.由于0是g（ζ-α）的重级至少为m的极点，所以G（0）/=0.

断言：G（k）（ζ）/=ζm.

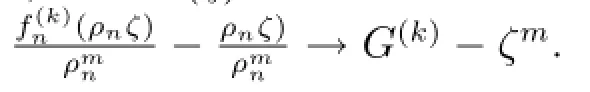
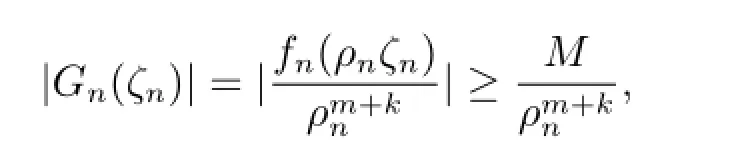
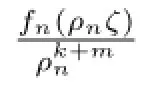
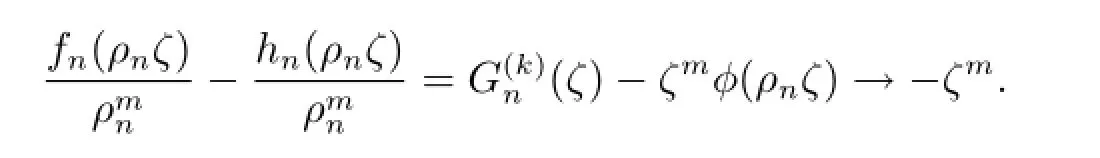
首先假设fn（z）在△δ∈△内上全纯函数.因为fn（z）在内正规，但是在0处不正规，由最大模型原理fn（z）→∞于内.

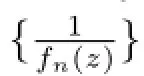
令

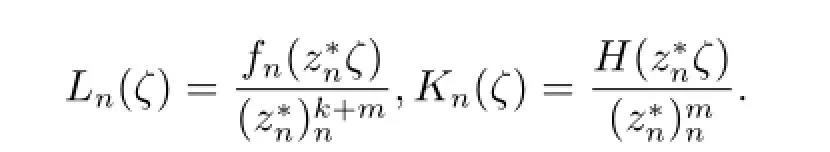
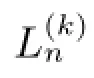
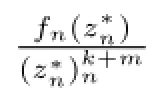
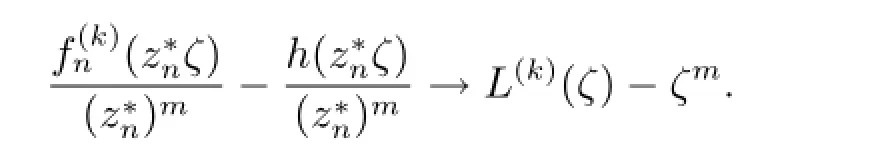
由Hurwitz定理，存在ζn，ζn→ζ0，使得当n分大时，，根据条件可得≥M，则

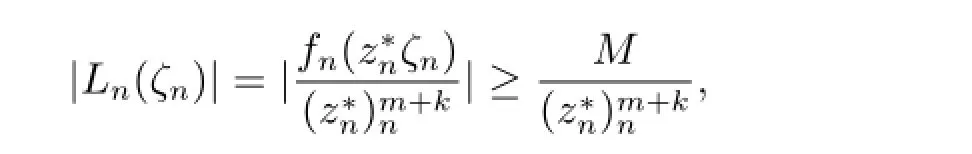
令

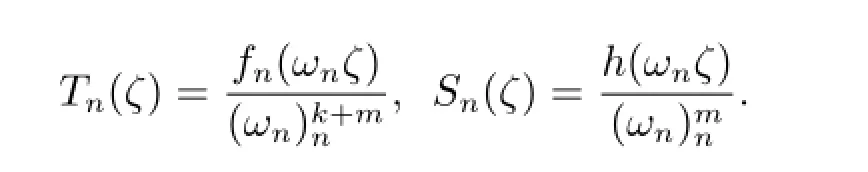
于是Tn（ζ）为复平面上的亚纯函数列，其零点的重级至少为k+3，Sn（ζ）为全纯函数列且一致收敛于ζm.根据条件可得（ζ）=Sn（ζ）⇒|Tn（ζ）|≥M，由引理2.7，Tn（ζ）在C｛0｝内正规.显然

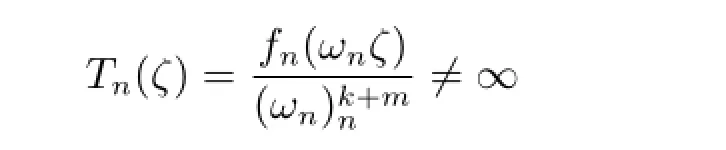
在△内.否则，存在ηn，使得Tn（ηn）=∞，则fn（ωnηn）=∞.显然|ωnηn|=|ωn||ηn|＜|ωn|，这与ωn是fn模最小的极点矛盾.再根据最大模原理以及Montel定则，故Tn（ζ）在C内正规.

设Tn（ζ）→T（ζ），其中T（ζ）的零点重级至少为k+3.显然，T（k）（ζ）-ζm有零点.否则，T（k）（ζ）/=ζm，从而T（k）（0）/=0m.又因为Tn（0）=Gn（0）→0，而且T（ζ）的零点重级至少为k+3，则T（k）（0）=0，矛盾.显然，T（k）（ζ）≡ζm.否则，T（k）（1）≡1m.又由于

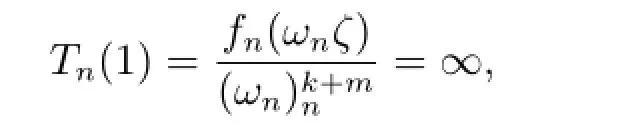
矛盾.于是设ζ0是T（k）（ζ）-ζm的零点，又因为

由Hurwitz定理，存在ζn，ζn→ζ0，使得当n分大时，（ωnζn）-h（ωnζn），根据条件可得|fn（ωnζn）|≥M，则

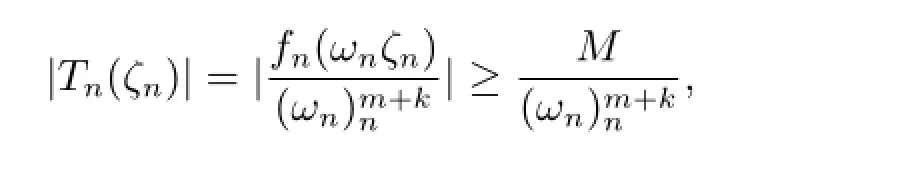
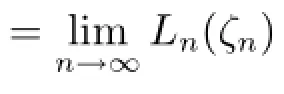
由于F∞在z0处正规，由条件知对于任意Fn∈F∞，有Fn（0）=∞，存在δ＞0，使得|F（z）|≥1在△δ内，所以当n充分大时，|Fn（z）|≥.故在△δ1内fn（z）/=0，则在△δ1内是全纯函数列，因此

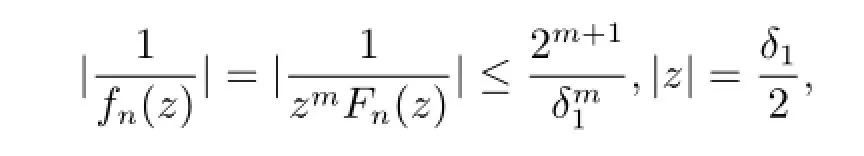
再由最大模原理以及Montel定则知F在z0处正规.故F在区域D内正规.

定理2的证明利用引理2.2和2.6，类似于定理1方法可证得.

［1］Gu Y X.A normal criterion of meromorphic families［J］.Sci.Sinica，Math.，1979，（I）：267-374.

［2］Yang L.Normality of families of meromorphic functions［J］.Scientia.Sinica.，1986，A（9）：898-908.

［3］Pang X C，Yang D G，Zalcman L.Normality families of meromorphic functions whose derivatives omit a function［J］.Comput.Meth.Funct.The.，2002，2：257-265.

［4］Pang X C，Zalcman L.Normal families and shared values［J］.Bull.London.Math.Soc.，2000，32：325-331.

［5］Xu Y.Picard Values and derivatives of meromorphic functions［J］.Kodai.Math.J.，2005，28：99-105.

［6］Wang Y F，Fang M L.Picard values and normal families of meromorphic functions with multiple zeros［J］.Acta Math.Sci.，1998，1：17-26.

［7］杨刘，陈巧玉.与例外函数相关的正规族［J］.华东师范大学学报，2013，2：154-159.

［8］Xu Y.Normal families and exceptional functions［J］.J.Math.Anal.Appl.，2007，329：1343-1354.

［9］李铭，黄斌.亚纯函数族的一个正规定则［J］.数学杂志，2014，3（34）：539-545.

［10］徐焱.亚纯函数的正规族［J］.数学杂志，2001，4（21）：381-386.

NORMALITY ON SHARING FUNCTIONS

YANG Duan-yang，YE Ya-sheng
（School of Science，University of Shanghai for Science and Technology，Shanghai 200093，China）

In this paper，we study the normality of the family of meromorphic functions about sharing functions.By using Nevanlinna theory method，we obtain a normal criterion，which improves a results got by Pang and Zalcman［3］.

normal family；sharing values；sharing functions；meromorphic function

MR（2010）主题分类号：30D45O174.52

A

0255-7797（2016）05-1091-06

2015-05-02接收日期：2015-06-02

国家自然科学基金项目（11371139）.

杨端阳（1989-），女，河南信阳，硕士，主要研究方向：复分析.

2010 MR Subject Classification：30D45