连续时间非时齐马氏过程的广义Dobrushin系数的估计

宋娟，张铭

（1.湖北经济学院统计学院，湖北武汉430205）

（2.中国政法大学科学技术教学部，北京102249）

连续时间非时齐马氏过程的广义Dobrushin系数的估计

宋娟1，张铭2

（1.湖北经济学院统计学院，湖北武汉430205）

（2.中国政法大学科学技术教学部，北京102249）

本文研究了非时齐马氏过程的广义Dobrushin系数的估计问题.在将经典Dobrushin遍历系数推广为加权的遍历系数的基础上，利用了矩阵拆分的方法，得到了对这种广义遍历系数的估计方法，推广了时齐马氏过程关于遍历系数的估计结果，借此可进一步得到有关遍历性的判定结论.

非时齐马氏过程；遍历系数；V范数

1　引言

在研究遍历性的问题时会涉及到很多不同的方法：如最小非负解理论，谱理论，泛函不等式以及遍历系数等，其中应用遍历系数来进行遍历性推断的的方法是一种较为简便且实用的方法.

遍历系数有很多种，其中最重要也是最常用的一种就是Dobrushin遍历系数δ（P）. Rhodius［10］和Neumann，Schneider［9］都曾研究过一些不同范数下的遍历系数，并证明了这些遍历系数都可以被Dobrushin遍历系数所控制.

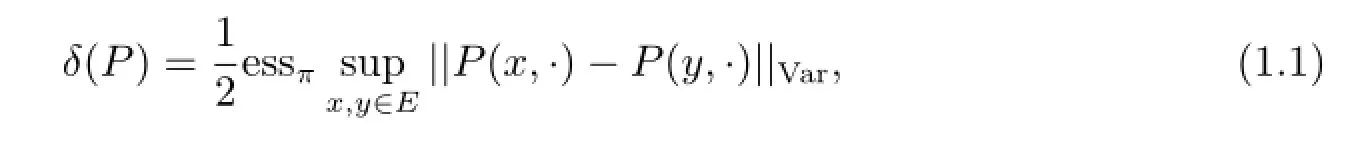
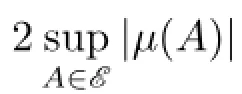
关于δ系数的研究已经进行了很多年，并且得到了很多重要的结果［2］.

近些年来，Hairer，Mattingly［5，6］等人在Meyn，Tweedie［8］的基础上，通过引入V范数，推广得到了LV空间及其对偶空间，并在其上讨论指数收敛、多项式收敛、次指数收敛等一系列问题，综合了drift条件、Lyapunov函数等得到了很好的结果.V范数实际上可以看作是一般常用范数的推广，在应用其进行具体研究时，可以发现它开拓了研究视野，提供了新的方法和理念，使研究过程得到简化.因此，越来越多的人投身于V范数的相关研究中，并将其推广到了更广泛的领域.文献［7］就是将V范数的概念与δ系数、遍历性相联系，推广得到了δV系数：定义符号测度µ的V范数为||µ||V：=sup｛∫Efdµ：||f||V≤1｝，其中V：E→［1，∞］是一个π-a.s.的有限函数，

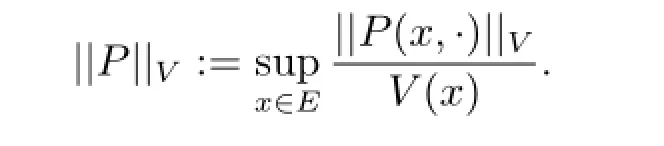
由此就将δ（P）推广为δV（P）.

定义1对于函数V：E→［1，∞），定义随机概率矩阵P关于V的广义Dobrushin系数为

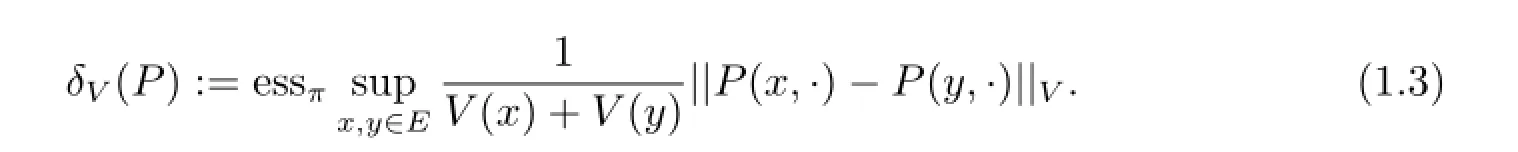
根据这个定义，显然有δV（I）=1.并且由此得到了指数遍历的另一种判定方法.

一个ψ不可约非周期的马氏链X=（Xn）n≥0是指数遍历的当且仅当X是遍历的且其不变测度为π，还存在一个π-a.s.有限函数V：E→［1，∞］使得π（V）＜∞并且当n足够大时有δV（Pn）＜1.

由此可以看出δV（P）与遍历性有直接的联系，因此对遍历性的判定就转换为了对δV（P）的估计问题.其实从文献［7］中的相关性质可以很明显的看出，对于离散时间的马氏链来说有

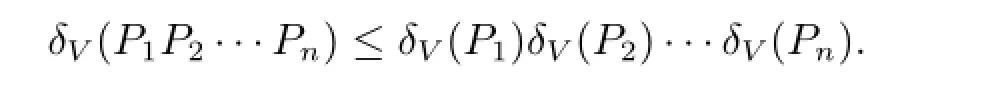
既然离散时间的δV（P）是被连乘积的形式控制的，那么连续时间时又是怎样的情形呢？

2　主要结果和证明

为了结果陈述的方便，先给出一些基本符号及假设.假设状态空间E上的非时齐的连续时间马氏过程Ps，t满足以下条件

（1）对任意的t≥u≥s≥0，都有Ps，t=Ps，uPu，t；

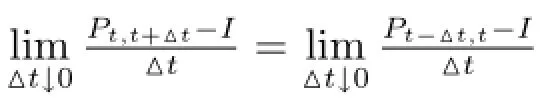
定理2对于非时齐的连续时间马氏过程Ps，t，若有supiqi（t）＜∞，t≥0，则

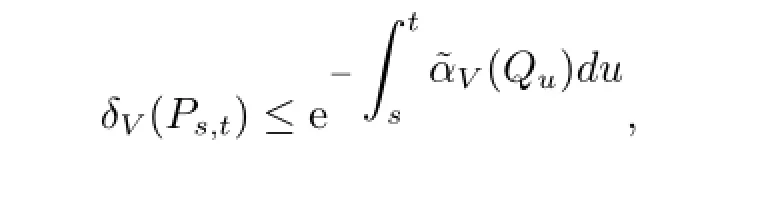
其中

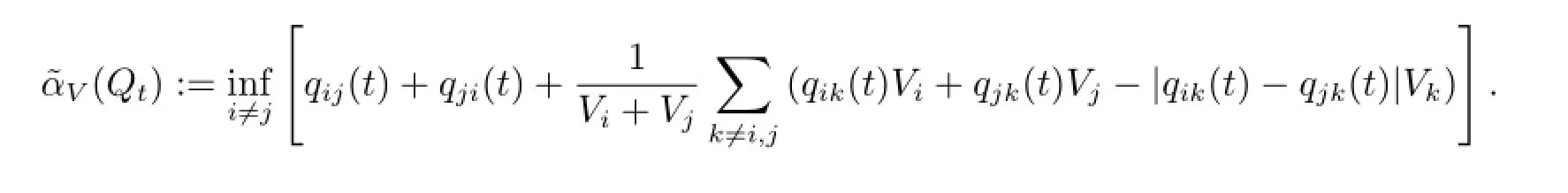
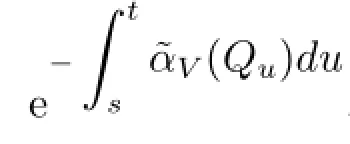
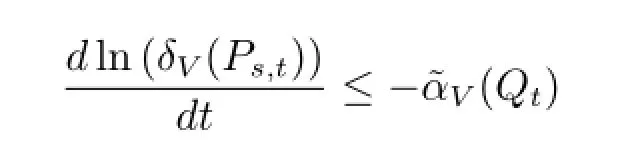
即可.这里用到文献［7］中证得的关于δV（P）系数的一个非常重要的性质

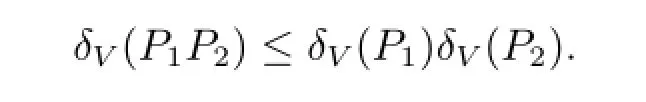
由此可以得出对于所有的s＜t，都有

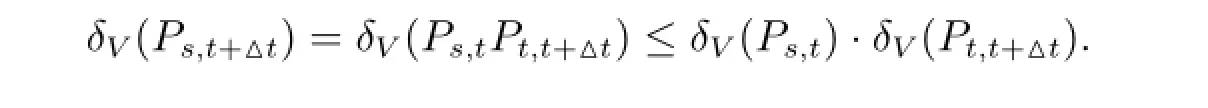
也就是

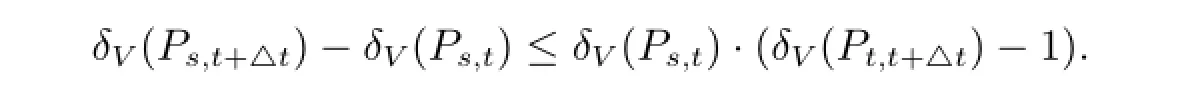
那么对于所有的△t＞0来说就有

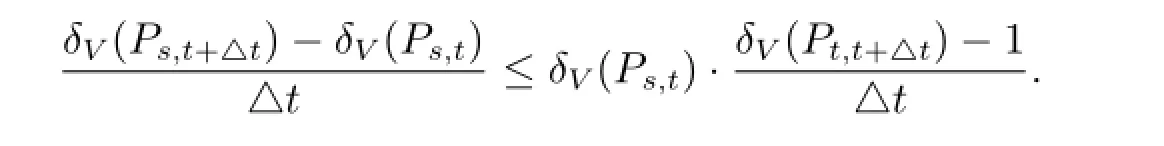
此时再令△t↓0，即得

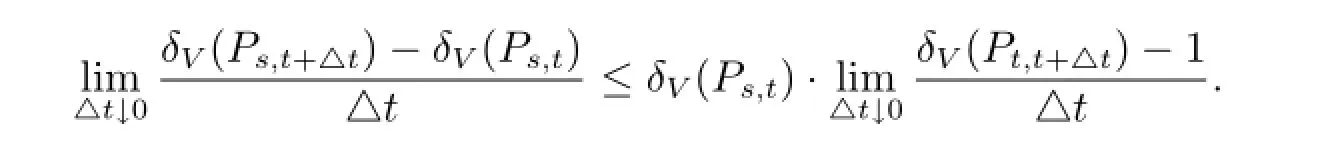
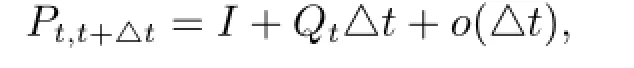
也就是Pt，t+△t具有如下矩阵形式

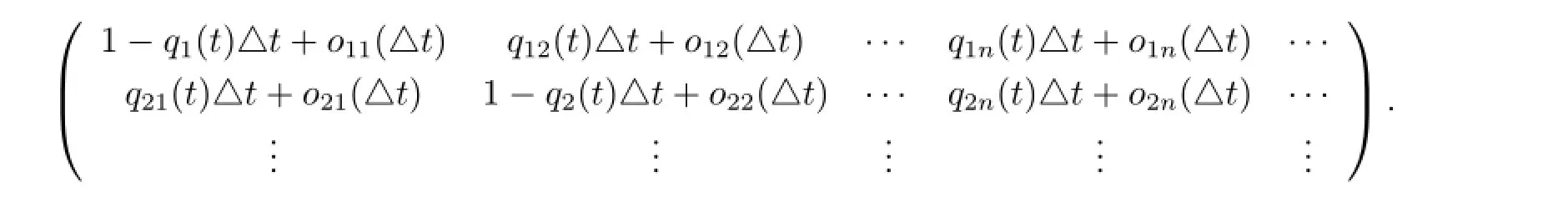
再根据δV（P）的定义，有

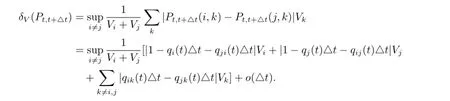
此时考虑到，由于supiqi（t）＜∞，所以存在εt＞0，使得对于任意的△t＜εt时都有

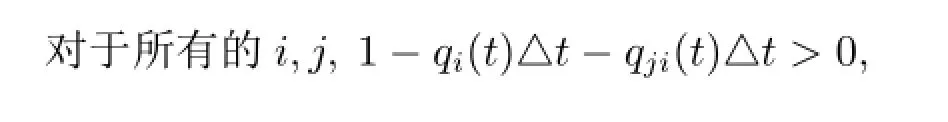
于是可以得到

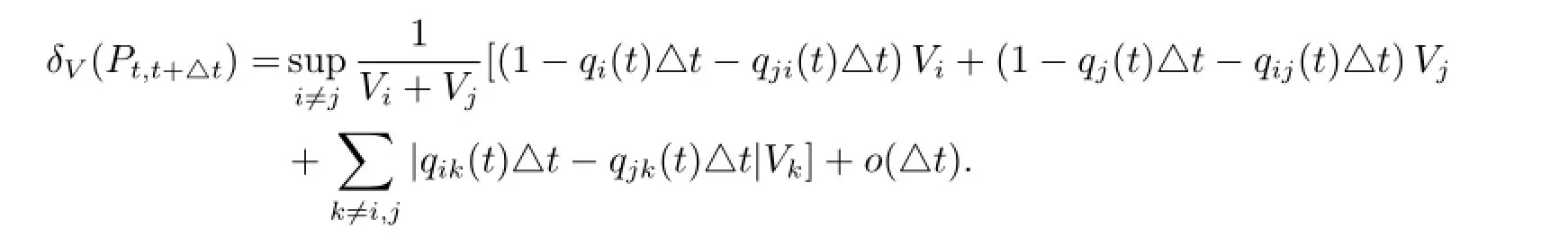
则综上有

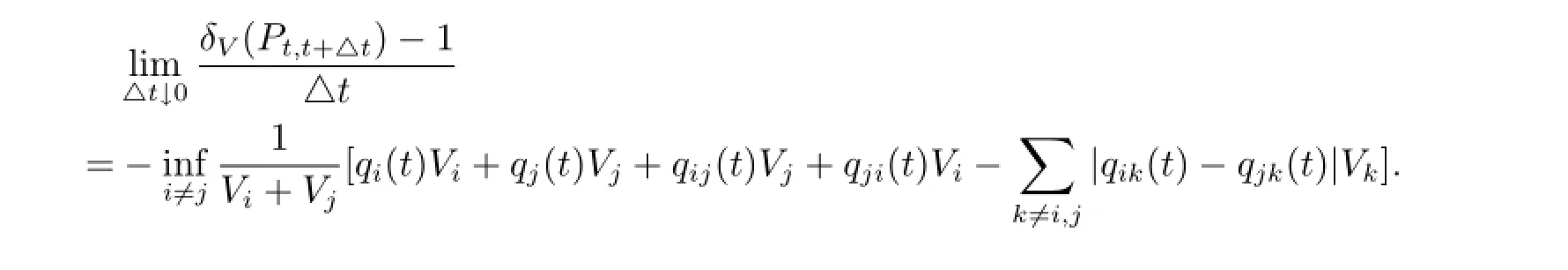
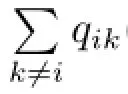
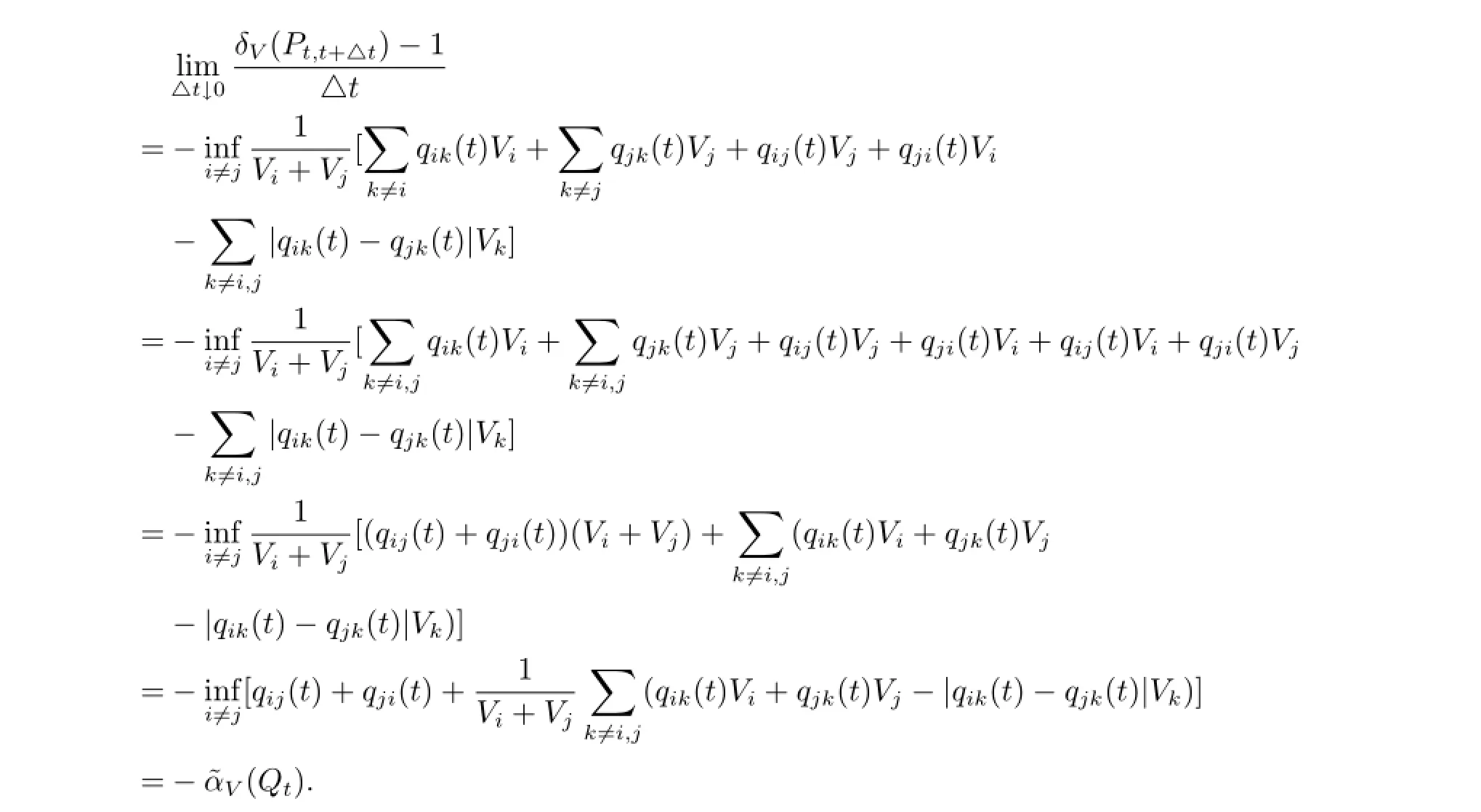
于是综上可知

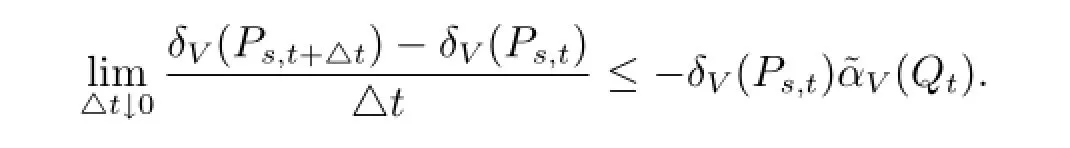
类似的方法，也可以得到

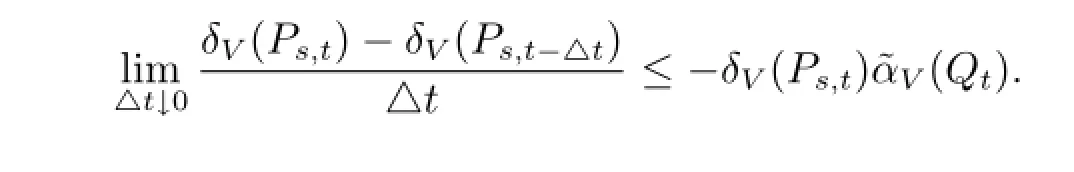
于是最终得到所要的

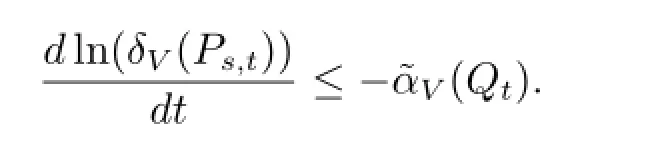
至此证明完毕.

根据前面的定义可知经典Dobrushin遍历系数就是当V（x）≡1时的特例，于是可得

推论3对于非时齐的连续时间马氏链Ps，t，若有supiqi（t）＜∞，t≥0，则

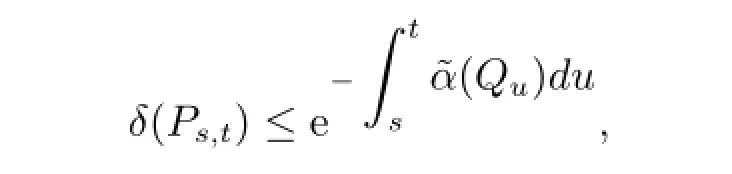
其中

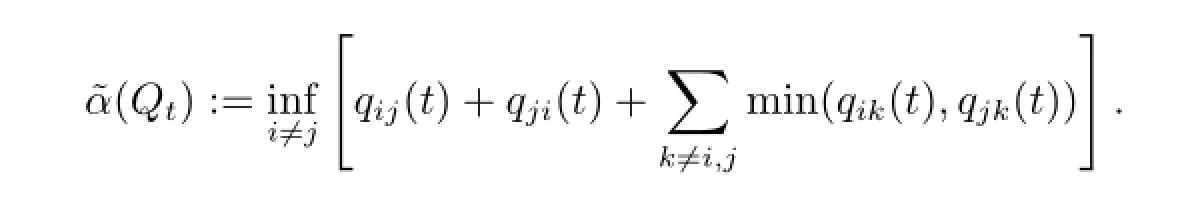
证此处只需令定理2中的V=1，即得

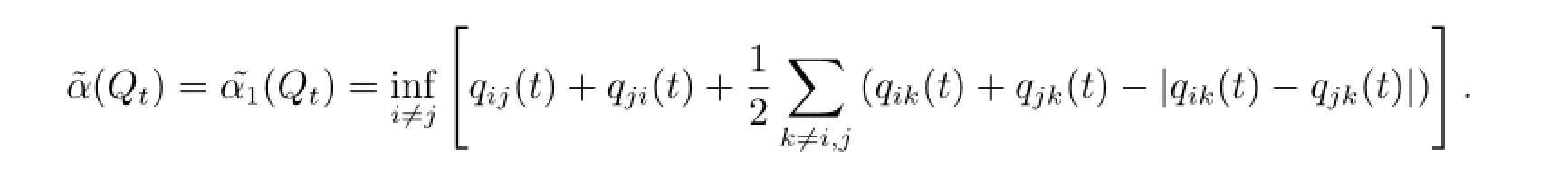
再由已知事实（a+b）-|a-b|=2min（a，b），即可得到结论.

这里的证明方法是从遍历系数本身的定义出发，使本文对其控制上界中的˜α和˜αV的来源有了更清楚的认识.由以上得到的结果可以看出，无论是δ系数还是δV系数，其在连续时间情形的控制上界都是由指数形式的控制量所控制的，这恰恰与离散时间的情况是相对应的.

［1］王伟刚，一般随机环境中马氏链的强大数律［J］.数学杂志，2011，31（3）：481-487.

［2］Anderson W J.Continuous-time Markov chains an applications-oriented approach［M］.New York：Springer-Verlag，1991.

［3］Chen Mufa.From Markov chains to non-equilibrium particle systems［M］.Beijing：World Scientufic，Second Edition，2004.

［4］Dobrushin R L.Central limit theorem for non-stationary Markov chains I，II［J］.The.Prob.Appl.，1956，1：63-80，329-383.

［5］Hairer M，Mattingly J C.Spectral gaps in Wassersttein distances and the 2D stochastic Navier-Stokes equations［J］.Ann.Prob.，2008，36（6）：2050-2091.

［6］Hairer M，Mattingly J C.Yet another look at Harris'ergodic theorem for Markov chains［J］.Seminar Stoch.Anal.Rand.Fiel.Appl.VI，Prog.Prob.，2011，63：109-117.

［7］Mao Yonghua，Zhang Ming，Zhang Yuhui.A generalization of Dobrushin coefficient［J］.Chinese J. Appl.Prob.Stat.，2013，29（5）：489-494.

［8］Meyn S P，Tweedie R L.Markov chains and stochastic stability［M］.London：Springer-Verlag，1996.

［9］Neumann M，Schneider H.The convergence of general products of matrices and the weak ergodicity of Markov chains［J］.Linear Alg.Appl.，1999，287：307-314.

［10］Rhodius A.On the maximum of ergodicity coefficients，the Dobrushin ergodicity coefficient，and products of stochastic matrices［J］.Linear Alg.Appl.，1997，253：141-154.

THE ESTIMATE OF GENERALIZED ERGODIC COEFFICIENT FOR CONTINUOUS-TIME INHOMOGENEOUS MARKOV PROCESSES

SONG Juan1，ZHANG Ming2
（1.School of Statistics，Hubei University of Economics，Wuhan 430205，China）
（2.Department of Science and Technology，China University of Political Science and Law，Beijing 102249，China）

In this paper，we study the estimate of the generalized ergodic coefficient for inhomogeneous Markov processes.On the basis of the generalization of the classical Dobrushin ergodic coefficient and using the matrix，we obtain the estimate of the generalized ergodic coefficient，which extends the result of the estimation of the ergodic coefficient for homogeneous Markov processes，with which we can get a criterion for the geometric ergodicity.

inhomogeneous Markov processes；ergodic coefficient；V-norm

MR（2010）主题分类号：37A30；60J27O211.62

A

0255-7797（2016）05-1097-06

2015-11-05接收日期：2015-12-23

中国政法大学青年教师科研启动资助项目（10816108）；国家社科项目“社交网络对社会稳定性影响的统计研究”（15CTJ006）.

宋娟（1981-），女，湖北武汉，讲师，主要研究方向：基础数学.

张铭.

2010 MR Subject Classification：37A30；60J27