ESSENTIAL NORMS OF THE GENERALIZED VOLTERRA COMPOSITION OPERATORS
JIANG Zhi-jie
(School of Science,Sichuan University of Science and Engineering,Zigong 643000,China)
ESSENTIAL NORMS OF THE GENERALIZED VOLTERRA COMPOSITION OPERATORS
JIANG Zhi-jie
(School of Science,Sichuan University of Science and Engineering,Zigong 643000,China)

Bergman-type space;weighted Zygmund space;generalized Volterra composition operator;essential norm
2010 MR Subject Classification:47B37;47B38
Document code:AArticle ID:0255-7797(2016)05-0929-11
1 Introduction
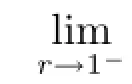

and

For 0<p<∞and the normal weight function u,the Bergman-type space Apuon D is defined by

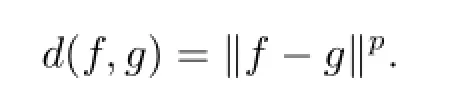
For this space and some operators,see,e.g.,[2]and[3].
For 0<β<∞,the weighted Bloch space Bβconsists of all f∈H(D)such that
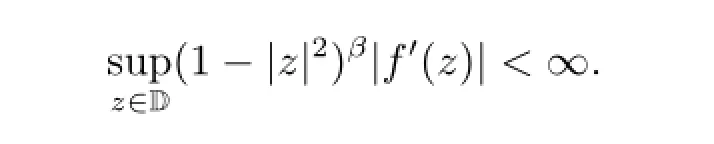
It is a Banach space under the norm
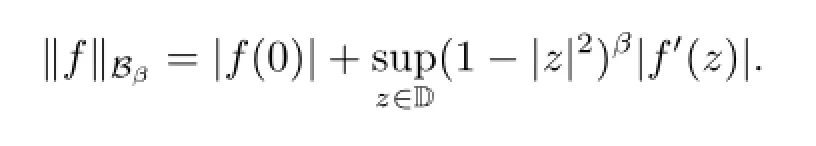
Similar to the weighted Bloch space,the weighted Zygmund spaceis defined by
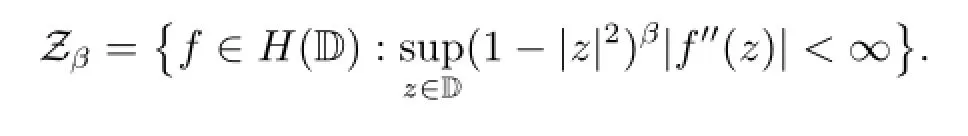
The norm on this space is

and under this norm it is a Banach space.There are a lot of papers to study weighted Bloch spaces,weighted Zygmund spaces and operators between weighted Bloch spaces or weighted Zygmund spaces and some other analytic function spaces.We refer the readers to see,e.g.,[4-8]and the references therein.
Let φ be an analytic self-map of D and g∈H(D).The Volterra composition operator Jφ,gon H(D)is

In the beginning,people studied this operator for the case φ(z)=z(see[1,9-12]).For this case,it is called the integral operator or the Volterra operator.People pay a lot of attention to this operator on analytic function spaces,due to it's relation with other branches of complex analysis such as,Bekoll´e-Bonami weights,univalent functions,Littlewood-Paley type formula,conformal invariance spaces and Carleson measures(see[1,9,10,13-15]). Recently,Li characterized the bounded and compact Volterra composition operators between weighted Bergman spaces and Bloch type spaces in[16].Wolf characterized the bounded and compact Volterra composition operators between weighted Bergman spaces and weighted Bloch type spaces in[17].The present author studied the bounded and compact Volterra composition operators from Bergman-type spaces to Bloch-type spaces and obtained an asymptotic expression of the essential norm in[2].
Let n be a nonnegative integer,φ an analytic self-map of D and g∈H(D).We define a generalized Volterra composition operatoron H(D)by

where f(0)=f.It is easy to see that this operator is a generalization of the Volterra composition operator.A natural problem is how to provide a function theoretic characterization of φ and g when they induce the bounded and compact operator between analytic function spaces in the unit disk.In this paper,we consider this problem for operatorfrom Bergman-type spaces to weighted Zygmund spaces and weighted Bloch spaces.We obtain the following Theorems 3.1,3.3.
Throughout this paper,constants are denoted by C,they are positive and may differ from one occurrence to the other.The notation ab means that there is a positive constant C such that a/C≤b≤Ca.
2 Prerequisites
First,we have the following lemma.Since the proof is standard,it is omitted(see Proposition 3.11 in[13]).
Lemma 2.1Suppose that φ is an analytic self-map of D,g∈H(D),Y=Bβor, and the operator→Y is bounded,then the operator→Y is compact if and only if for bounded sequence{fj}insuch that fj→0 uniformly on every compact subset of D as j→∞,it follows that

For the cases of j=0 and j=1,the next lemma was proved in[4].For the general positive integer j,it can be proved similarly,and it is omitted here.
Lemma 2.2For j∈N+,there is a positive constant C independent of f∈such that for every z∈D the following inequality holds
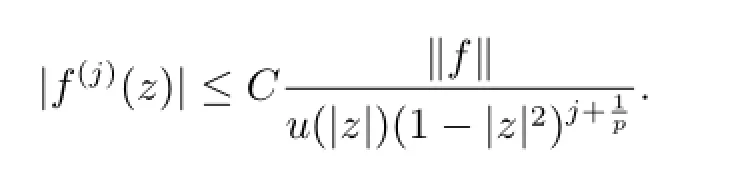
The next Lemma 2.3 can be found in[4].
Lemma 2.3Suppose that w∈D,then for t≥0 the function

Using the function fw,t,we have
Lemma 2.4Suppose that w∈D,then for each fixed j∈{1,2,···,n}there exist constants c1,c2,···,cnsuch that the function

satisfying
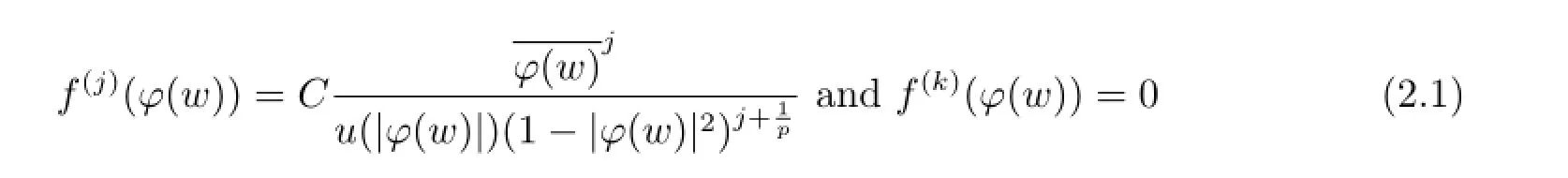
for each k∈{1,2,···,n}{j},where C is a constant related to j.
ProofFor a fixed w∈D and arbitrary constants d1,d2,···,dn,define the function

To finish the proof,we only need to show that there exist constants d1,d2,···,dnsuch that f satisfying assertion(2.1).By calculating f(k)for each k∈{1,···,n},we obtain the following linear system

If we can show that the determinant of this linear system is different from zero,the problem will be solved.Applying Lemma 2.3 in[18]with a=n+1/p>0,we see that it is different from zero.Let ci=di/(n-2+i+),and then proof is end.
The following lemma is also a folklore.
Lemma 2.5H∞⊆In particular,every polynomial function belongs to
3 Main Results
We first give the conditions forto be a bounded operator.
Theorem 3.1Suppose that φ is an analytic self-map of D and g∈H(D),then the operatoris bounded if and only if the following conditions are satisfied

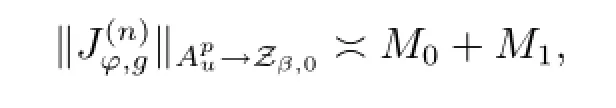
ProofFirst suppose that the operatoris bounded.Take the function f(z)=zn/n!.Then from Lemma 2.5 it follows that f∈Since the operatoris bounded,we have

that is

Considering f(z)=zn+1/(n+1)!,by the boundedness of the operatorwe have

From(3.1),(3.2)and the fact|φ(z)|<1 on D,it follows that

For w∈D,taking the function f in Lemma 2.4,we know that there exist constants c1,c2,···,cn+1such that
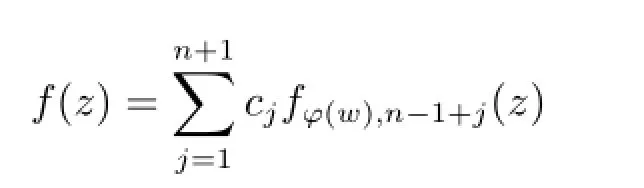
satisfying

and f(k)(φ(w))=0 for each k∈{1,2,···,n}.Then by the boundedness of the operator,we get
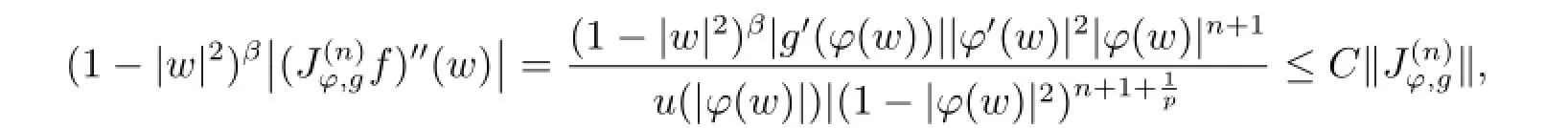
i.e.,we have
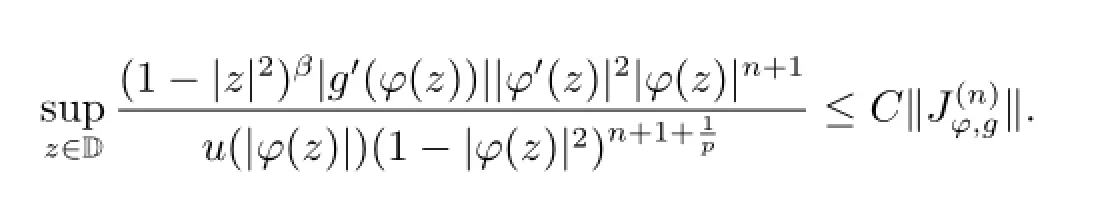
So for δ∈(0,1),
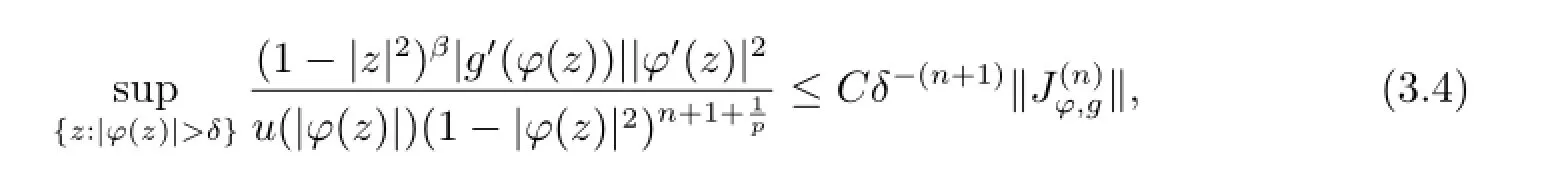
and by(3.3),
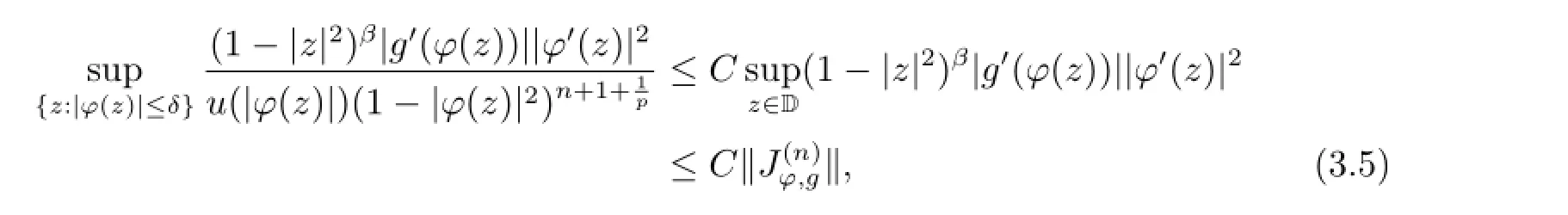
where the first constant

From(3.4)and(3.5),assertion(i)follows.
Once again choose the function f in Lemma 2.4 which satisfies

and f(k)(φ(w))=0 for each k∈{1,2,···,n-1,n+1}.Then by the similar method,we can prove that assertion(ii)is true,and the proof is omitted here.
Conversely,suppose that assertions(i)and(ii)hold.For f∈by Lemma 2.2 we have

From assertions(i),(ii)and(3.6),it follows thatis bounded.From the above inequalities,we also obtain the asymptotic expression
The following result can be similarly proved.
Theorem 3.2Suppose that φ is an analytic self-map of D and g∈H(D),then the operatoris bounded if and only if
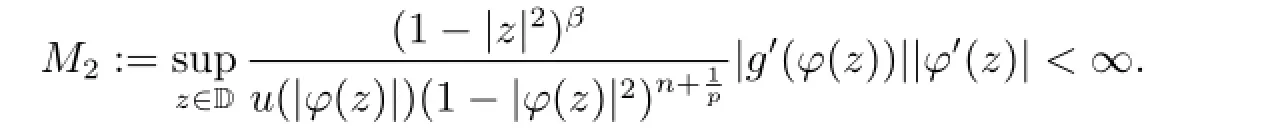
We begin to estimate the essential norm of the generalized Voterra composition operators.Let us recall the definition of the essential norm of the bounded linear operators. Suppose that X and Y are Banach spaces and T:X→Y is a bounded linear operator,then the essential norm of the operator T:X→Y is defined by

where K denotes the set of all compact linear operators from X to Y.By the definition,it is clear that the bounded linear operator T:X→Y is compact if and only if
Theorem 3.3Suppose that φ is an analytic self-map of D,g∈H(D)andis bounded,then

where the sequence{zj}satisfies|φ(zj)|→1-as j→∞.
ProofSuppose that{zj}is a sequence in D such that|φ(zj)|→1-as j→∞. For each φ(zj),taking fjthe function in the proof of Theorem 3.1,we have seen that maxj∈N‖fj‖≤C,and it is obvious that fj→0 uniformly on compacta of D as j→∞. Hence for every compact operator K:→,we have‖Kfj‖→0 as j→∞.Thus it follows that
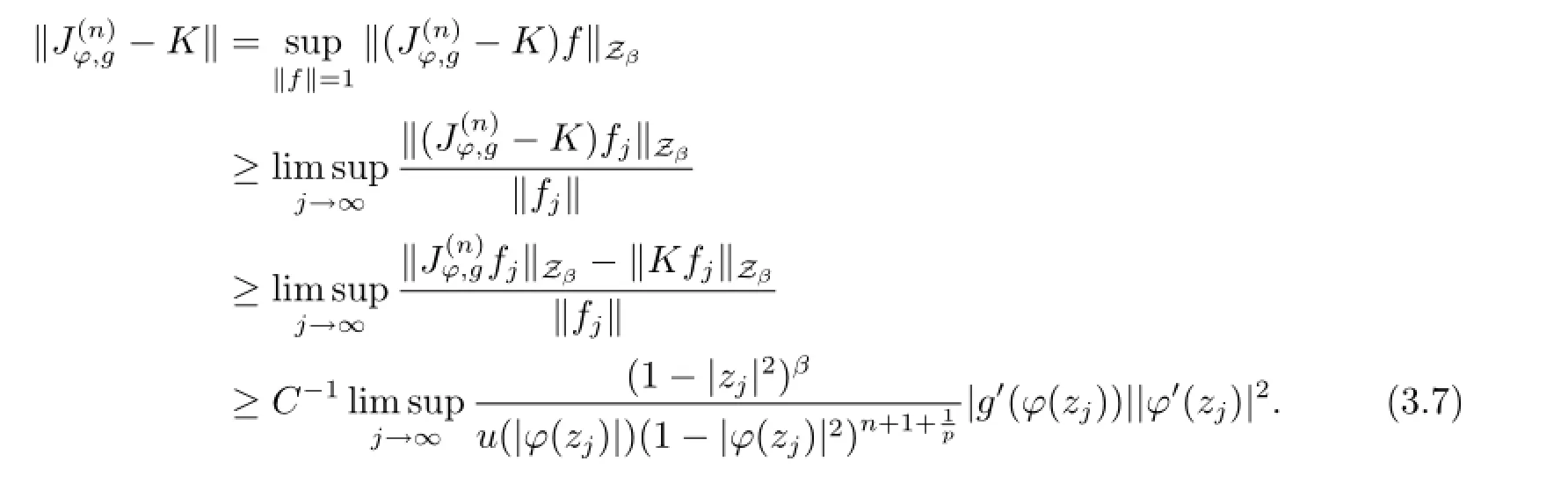
By taking the infimum in(3.7)over the set of all compact operators K:,we obtain

Using the similar method,we also have

Combing these inequalities,we have got

Now suppose that{rj}is a positive sequence which increasingly converges to 1.For every rj,we define the operator by








Similar to the proof of Theorem 3.3,we can also prove the next result.
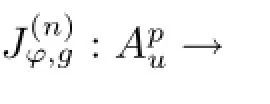
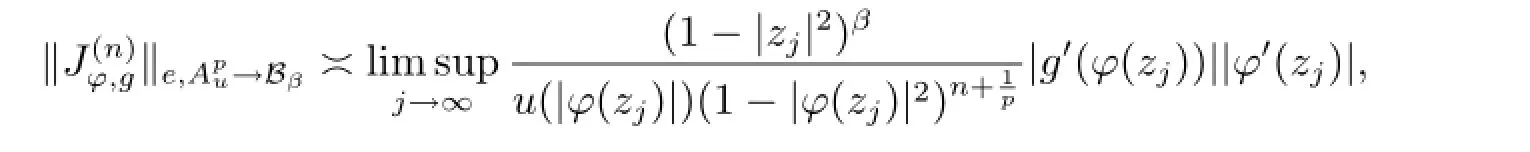
where the sequence{zj}satisfies|φ(zj)|→1-as j→∞.
So we have


References
[1]Aleman A,Cima J A.An integral operator on Hpand Hardy's inequality[J].J.Anal.Math.,2001,85:157-176.
[2]Jiang Z J.On Volterra compositon operators from Bergman-type space to Bloch-type space[J]. Czech.Math.J.,2011,61(136):993-1005.
[3]Li X S,Stevi´c S.Weighted composition operators from Bergman-type spaces into Bloch spaces[J]. Proc.Indian Acad.Sci.,2007,117:371-385.
[4]Jiang Z J.On a class of opertors from weighted Bergman spaces to some spaces of analytic functions[J].Taiwan.J.Math.Soc.,2011,15(5):2095-2121.
[5]Li X S,Stevi´c S.Weighted composition operators from Zygmund spaces into Bloch spaces[J].Appl. Math.Comput.,2008,206(2):825-831.
[6]Ohno S.Weighted composition operators between H∞and the Bloch space[J].Taiwan.J.Math. Soc.,2001,5(3):555-563.
[7]Ohno S.Products of composition and differentiation on Bloch spaces[J].Bull.Korean Math.Soc.,2009,46(6):1135-1140.
[8]Yang W.Weighted composition operators from Bloch-type spaces to weighted-type spaces[J].Ars. Combin.,2009,93:265-274.
[9]Aleman A,Siskakis A G.An integral operator on Hp[J].Compl.Var.The.Appl.,1995,28:149-158.
[10]Aleman A,Siskakis A G.Integration operators on Bergman spaces[J].Indiana Univ.Math.J.,1997,46:337-356.
[11]Siskakis A G,Zhao R H.An Volterra type operator on spaces of analytic functions[J].Funct.Spaces (Edwardville IL),1998:299-311.
[12]Xiao J.Riemann-Stieltjes operators on weighted Bloch and Bergman spaces of unit ball[J].J.London.Math.Soc.,2004,70(2):199-214.
[13]Cowen C C,MacCluer B D.Composition operators on spaces of analytic functions[M].New York:CRC Press,1995.
[14]Pommerenke Ch.Schlichte funktionen und analytische funktionen von beschr¨ankter mittlerer oszillation[J].Comment.Math.Helv.,1977,52:591-602.
[15]Shapiro J H.Composition operators and classical function theory[M].New York:Springer-Verlag,1993.
[16]Li X S.Volterra composition operators between weighted Bergman spaces and Bloch type spaces[J]. J.Korean Math.Soc.,2008,45:229-248.
[17]Wolf E.Volterra composition operators between weighted Bergman spaces and weighted Bloch type spaces[J].Collect.Math.,2010,61:57-63.
[18]Stevi´c S.Composition operators from weighted Bergman spaces to the n-th weighted spaces on the unit disc[J].Discr.Dyn.Nat.Soc.,Vol.2009,Artical ID 742019,11 page.
推广的Volterra复合算子的本性范数
江治杰
(四川理工学院理学院,四川自贡643000)
本文研究单位圆盘上Bergman型空间到Zygmund型空间上的一类推广的Volterra复合算子.利用符号函数φ和g刻画这类算子的有界性、紧性,并计算其本性范数.
Bergman型空间;加权Zygmund空间;推广的Volterra复合算子;本性范数
MR(2010)主题分类号:47B37;47B38O174.56
date:2014-03-13Accepted date:2014-06-23
Supported by the National Natural Science Foundation of China(11201323);the Sichuan Province University Key Laboratory of Bridge Non-destruction Detecting and Engineering Computing(2013QZJ01)and the Introduction of Talent Project of SUSE(2014RC04).
Biography:Jiang Zhijie(1979-),male,born at Anqiu,Shandong,associate professor,major in functional analysis.
———理学院

