关于一类广义Ramanujan-Nagell方程的正整数解

张正萍，赵开明

（1.重庆科技学院数理学院，重庆401331）

（2.重庆求精中学，重庆400015）

关于一类广义Ramanujan-Nagell方程的正整数解

张正萍1，赵开明2

（1.重庆科技学院数理学院，重庆401331）

（2.重庆求精中学，重庆400015）

本文研究了一类广义Ramanujan-Nagell方程有正整数解的条件.利用二次域中的重要理论，给出了一个典型的Ramanujan-Nagell方程的所有正整数解，推广了文献［1］和［2］的结果.

广义Ramanujan-Nagell方程；正整数解；二次域

1　引言

设Z和N分别表示全体整数和正整数组成的集合，p是奇素数，D是适合p/|D的正整数.此时，方程

是一类基本而重要的广义Ramanujan-Nagell方程.多年来，关于该类方程的整数解一直是指数Diophantus方程的一个引人关注的问题，但主要是其解数N（D，p）的上界估计，乐茂华［1］证明了当（D，p）=（2，3）或（3s2+1，4s2+1），其中s是正整数时方程（1.1）恰有2组正整数解，否则，该方程至多有1组正整数解；曹珍富［2］仅给出了方程x2+2=3n仅有（1，1）、（5，3）两组正整数解.

作为代数数论中的重要组成部分，二次域的有关类数、理想等相关性质和理想数唯一分解定理对研究该类方程的整数解有着重要作用.对某些D＞0，不是Euclid域，若其类数=1，可以利用代数整数环中唯一分解定理的相关知识去研究方程的整数解问题；若其类数/=1，可以利用二次域中整数环上的理想唯一分解定理去研究方程的整数解问题.为此，先引入同余式、二次域的有关类数、理想及其相关性质和理想唯一分解定理.

定义1.1［3］若ε和ε-1都是代数整数，则ε称为单位数.

定义1.2［4］环R的非空子集S叫做R的理想，是指满足下面条件：（1）如果a，b∈S，则a±b∈S；（2）如果r∈R，a∈S，则ar，ra∈S.

定义1.3［4］由一个元素x∈R生成的理想（x）叫做环R的主理想，如果R是整环，并且R中每个理想都是主理想（x）=xR，则R叫做主理想整环.

定义1.4［5］数域K的子集I叫做K的分式理想，是指存在0/=µ∈Ok（数域K的整数环），使得µI为Ok的非零理想，用I（K）表示K的全体分式理想组成的集合，且I（K）构成群，叫做数域K的分式理想群；对于α∈K，称αOk（0/=α∈Ok）为主分式理想，而I（K）中主分式理想的全体构成一个群，叫做K的主分式理想群，记作P（K）；商群C（K）=I（K）/P（K），叫做K的（分式）理想类群，C（K）中的每一个元素叫做K的（分式）理想类.

定义1.5［5］理想类群的阶h（K）=|C（K）|叫做数域K的类数.

定义1.6［6］设是一个代数整数环，α1，α2，···，αs∈，把集合

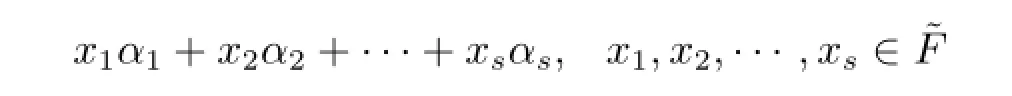
称为是由α1，α2，···，αs生成的˜F中的理想数.

定义1.7［6］设α，β∈M，若存在ε使β=ε⊙α，则称β是α的相伴数，记作β～α.

定理1.1［7］若a≡b（modmi），其中i=1，2，···，n，则a≡b（mod［m1，m2，···，mn］）.

引理1.1［6］α∈A2（全体Q上的2次代数数组成的集合）的充要条件是α=r+其中r，s∈Q，s/=0以及D/=0是无平方因子的有理整数全体Q上的2次代数整数组成的集合）的充要条件是除以上所说的外还要满足2r∈Z，～r2-Ds2∈Z.

引理1.2［6］设D满足引理1.1的条件，及

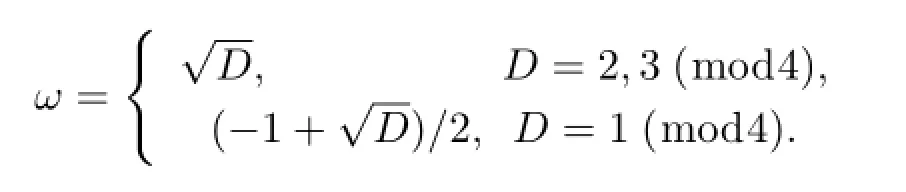
那么α是二次代数整数的充要条件是它可以表为

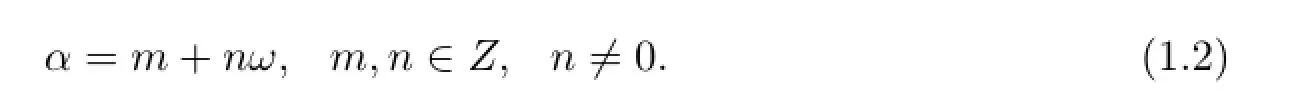
定理1.2［6］当D≤-1时，仅当D=-1，-3时才有形如（1.2）的单位数.仅当D=-1时，这种单位数是±i，当D=-3时，这种单位数是

定理1.3［6］主理想整环是唯一分解整环.

定理1.4［6］设M是唯一分解环，正整数k≥2，以及α，β∈M，（α，β）=，那么若αβ=γk，γ∈M，则有α=ε1µk，β=ε2νk，µ，ν∈M，其中ε1，ε2是M中的单位，且ε1ε2=εk，ε为单位.

2　x2+5=pn（n∈N）有正整数解的必要条件

利用二次域中整数环上的理想唯一分解定理，以下证明广义Ramanujan-Nagell方程

有正整数解的必要条件.

证情形（1）若n是偶数，则由（2.1）式可得

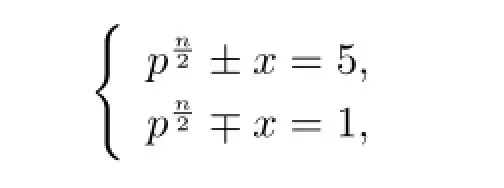
情形（2）若n是奇数，在虚二次域中，由定义1.4和定义1.5可得的类数=2，且有单位数±1，其中1和是一组整基［6］，从而整环的整数形如的形式，其中a，b∈Z.由此可得方程（2.1）的理想分解为

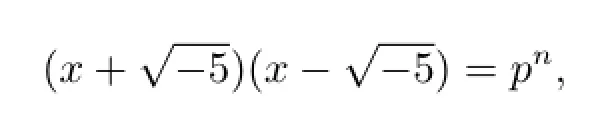
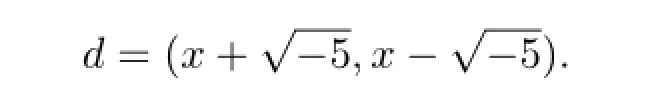
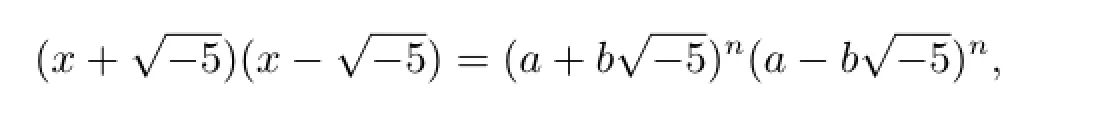
其中a2+5b2=p.从而由定理1.4得

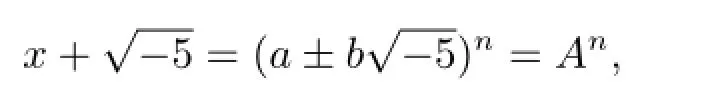
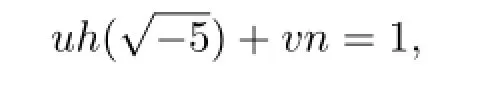
于是有

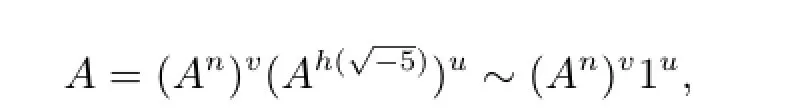
由An～1得A～1v，1u～1，即A是中的主理想.又由中的单位数是±1，则有

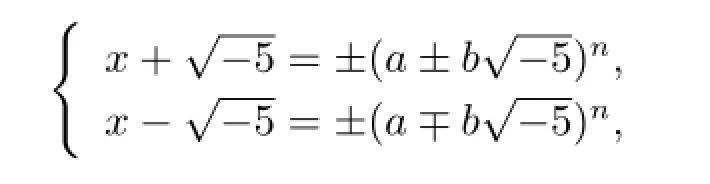
进而有

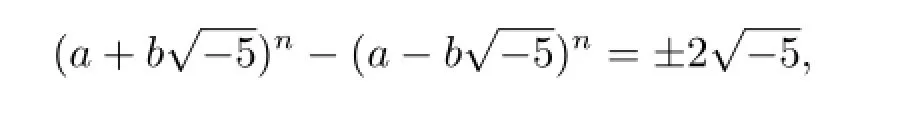
则

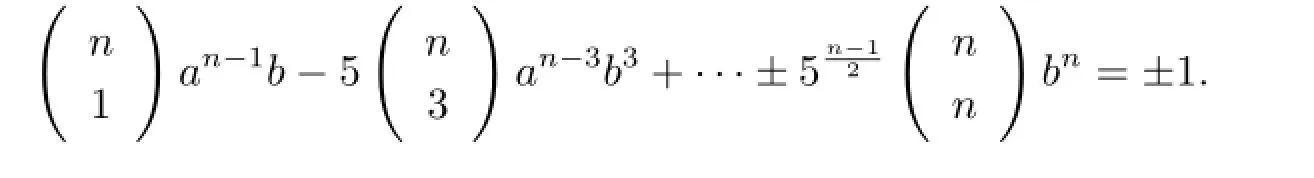
即

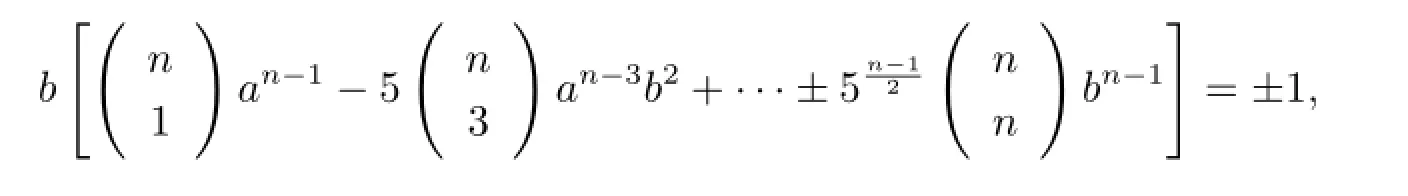
从而b=±1，得证.

3　x2+5=pn（n∈N）正整数解的证明

以下证明广义Ramanujan-Nagell方程

仅有正整数解（4，1）.

证情形（1）若n是偶数，则由（3.1）式可得

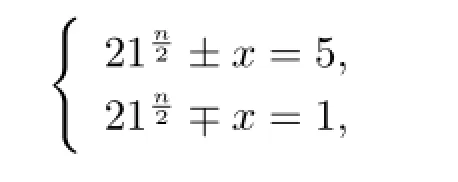
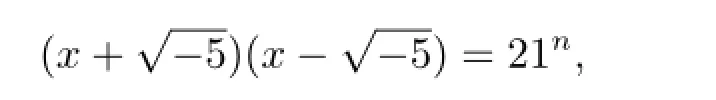
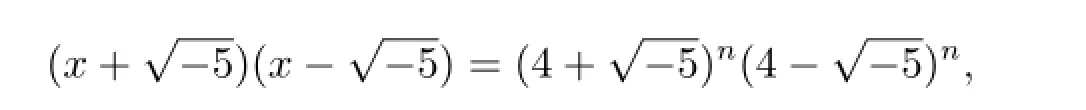
从而有

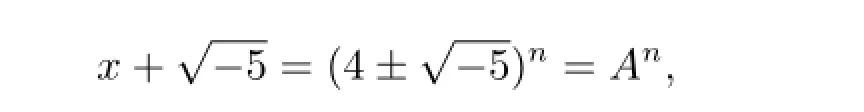
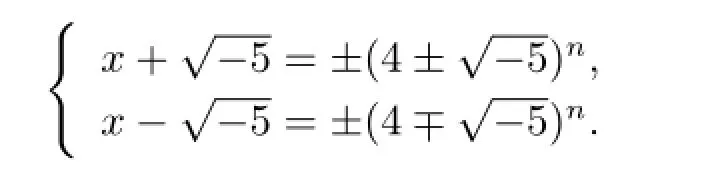
进而有

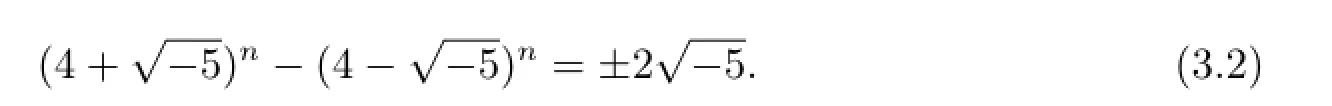
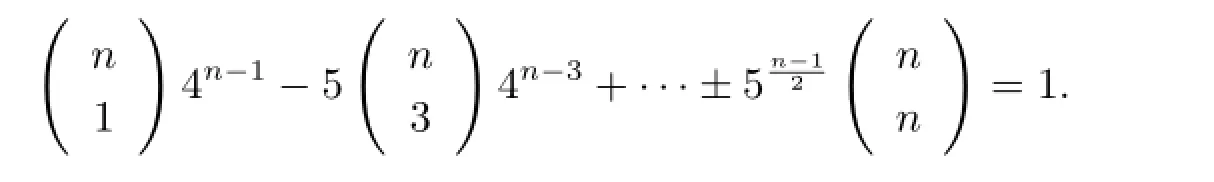
所以n·4n-1≡1（mod5）.故n·（-1）n-1≡1（mod5）.令f（n）≡n·（-1）n-1（mod5），由于其周期为10.即f（10n+k）≡f（k）（mod5）.故n≡1，4（mod10），又由条件n是奇数知n≡1（mod2），从而由定理1.1得n≡1（mod10）.当n=1时，方程有正整数解（x，n）=（4，1）.

下证方程（3.1）的指数n不能有两个不同的解n1和n2，满足n1-n2≡0（mod10）.否则，可设

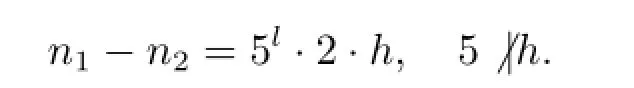
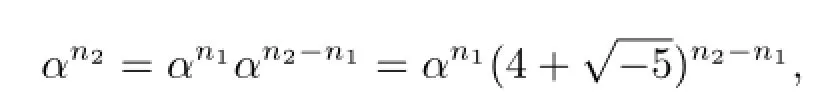
对于5l+1的方幂实行数学归纳法可证

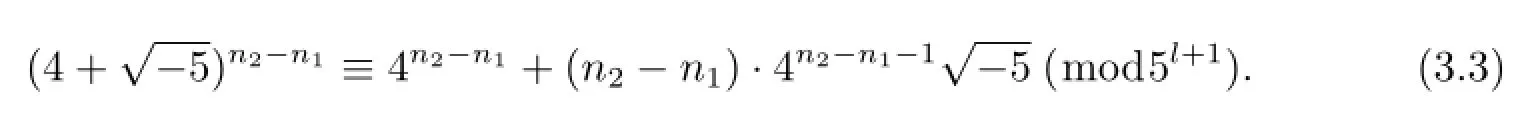
又因

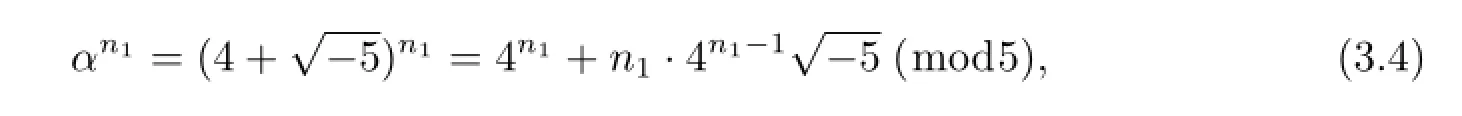
由（3.3）式和（3.4）式知

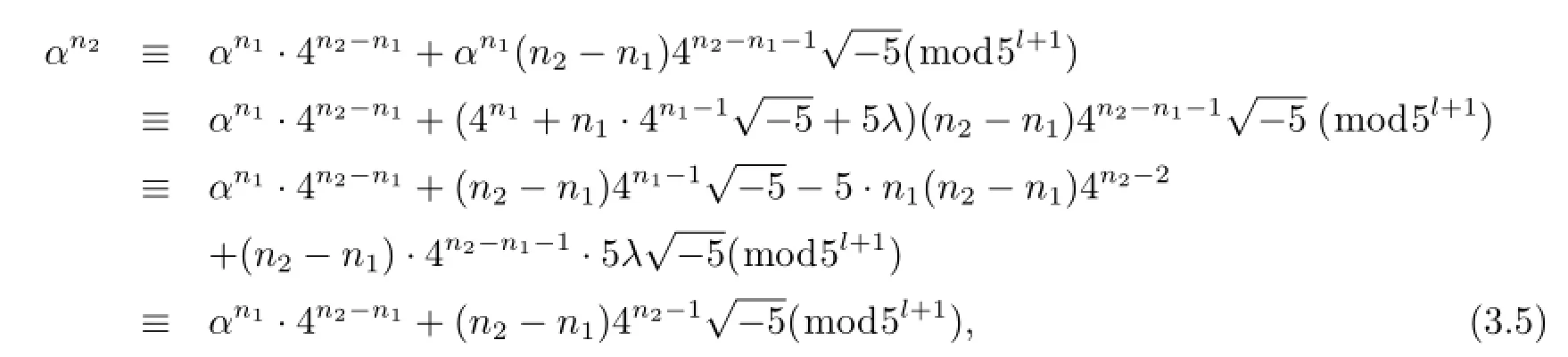
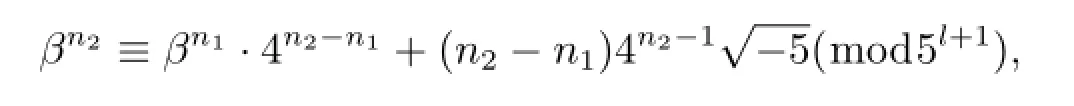
由于（3.2）式中的右端不能够取负号，即αn1-βn1=αn2-βn2.故

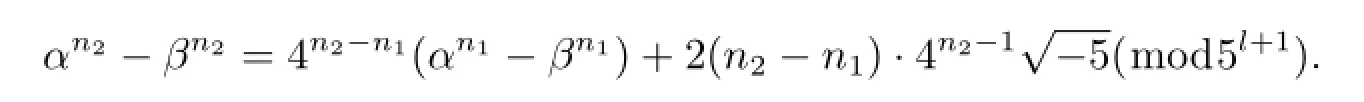
又因为n2-n1≡0（mod10），n1-1≡0（mod2），且4|n2-n1.即4n2-n1≡1（mod5）.所以有4n2-1≡±1（mod5）.故有

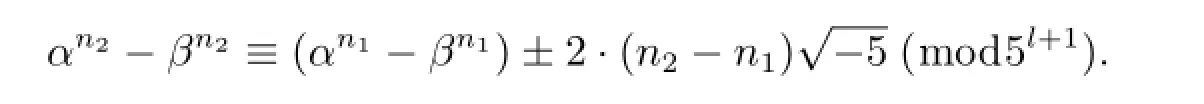
进而有

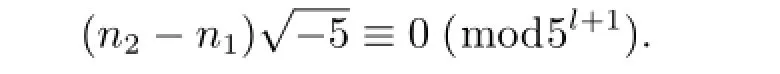
即

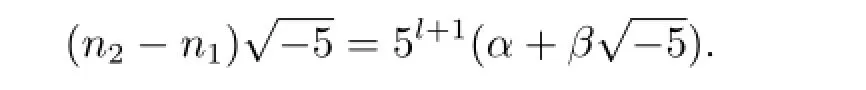
亦即

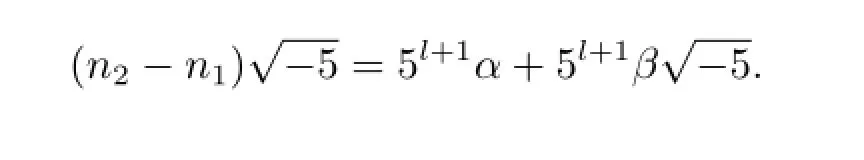
于是得

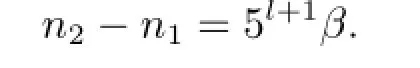
即n2-n1≡0（mod5l+1）.与5l/|n2-n1矛盾.故方程（3.1）的正整数解唯一，仅有（x，n）=（4，1），证毕.

［1］乐茂华.关于广义Ramanujan-Nagell方程x2+D=pn的解数［J］.常德师范学院学报（自然科学版），2002，14（1）：1-2.

［2］曹珍富.丢番图方程引论［M］.哈尔滨：哈尔滨工业大学出版社，2012.

［3］华罗庚.数论导引［M］.北京：科学出版社，1979.

［4］张禾瑞.近世代数基础（修订本）［M］.北京：高等教育出版社，2010.

［5］冯克勤.代数数论［M］.北京：科学出版社，2000.

［6］潘承洞，潘承彪.代数数论（第二版）［M］.济南：山东大学出版社，2001.

［7］闵嗣鹤，严士健.初等数论（第三版）［M］.北京：高等教育出版社，2003.

［8］杨仕椿.广义Ramanujan-Nagell方程x2+Dm=pn的解的注记［J］.数学学报，2007，50（4）：943-948.

［9］乐茂华.关于广义Ramanujan-Nagell方程的一点注记［J］.数学杂志，2007，27（2）：219-221.

［10］杨继明.广义Ramanujan-Nagell方程x2-D=3n的解数［J］.数学学报，2008，51（2）：351-356.

［11］陈候炎.关于广义Ramanujan-Nagell方程的一个猜想［J］.数学杂志，2010，50（4）：567-569.

［12］乐茂华，胡永忠.广义Lebesgue-Ramanujan-Nagell方程研究的新进展［J］.数学进展，2012，41（4）：385-393.

ON THE POSITIVE INTEGER SOLUTIONS OF A CLASS OF GENERALIZED RAMANUJAN-NAGELL EQUATION

ZHANG Zheng-ping1，ZHAO Kai-ming2
（1.School of Mathematics and Physics，Chongqing University of Science and Technology，Chongqing 401331，China）
（2.Chongqing Refinement School，Chongqing 400015，China）

In this paper，we studied the necessary condition for existence of the positive integer solutions of a class of generalized Ramanujan-Nagell equation.On the base of it，we gave all the positive integer solutions of a typical Ramanujan-Nagell equations，and generalized some results of reference［1］and［2］.

generalized Ramanujan-Nagell equation；positive integer solution；quadratic fields

MR（2010）主题分类号：11D45；11D75O156.7

A

0255-7797（2016）05-1077-06

2014-10-08接收日期：2014-12-24

重庆市自然科学基金项目（cstc2013jcyjA10049）；重庆科技学院本科教育教学改革研究项目（201249）.

张正萍（1973-），女，四川泸州，讲师，研究方向：数论.

2010 MR Subject Classification：11D45；11D75