3×3阶上三角算子矩阵的点谱和剩余谱扰动

黄俊杰，吴秀峰，阿拉坦仓

（内蒙古大学数学科学学院，内蒙古呼和浩特010021）

3×3阶上三角算子矩阵的点谱和剩余谱扰动

黄俊杰，吴秀峰，阿拉坦仓

（内蒙古大学数学科学学院，内蒙古呼和浩特010021）

基于值域的稠密性和闭性，有界线性算子T的点谱和剩余谱可分别细分为σp，1（T），σp，2（T）和σr，1（T），σr，2（T）.设H1，H2，H3为无穷维复可分Hilbert空间，给定A∈B（H1），B∈B（H2），C∈B（H3），结合分析方法与算子分块技巧给出了MD，E，F的上述四种谱随D，E，F扰动的完全描述.

算子矩阵；点谱；剩余谱；扰动

1　引言

缺少了某些元素的算子矩阵称为缺项算子矩阵.算子矩阵的谱补问题旨在讨论缺项算子矩阵中所缺的元素对整个算子矩阵谱的影响，在换位提升理论，插值理论，以及系统控制理论中具有重要应用.算子矩阵的谱扰动属于谱补问题的研究范畴，它是当所缺的元素跑遍特定的集合时整个算子矩阵谱的稳定的组成部分.

设H1，H2，H3为无穷维复可分Hilbert空间.以B（Hi，Hj）表示从Hi到Hj的所有有界（线性）算子构成的集合，B（Hi，Hi）简记为B（Hi），其中i，j=1，2，3.给定A∈B（H1），B∈B（H2），C∈B（H3），记

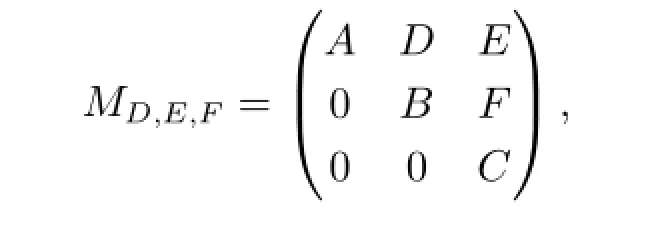
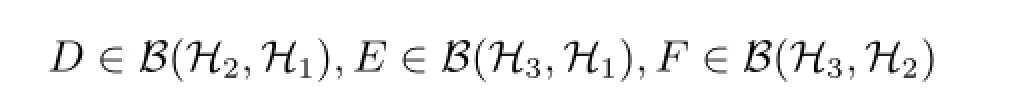
其中为待定的未知算子.显然，MD，E，F是H1⊕H2⊕H3上的缺项上三角算子矩阵.为叙述方便，对于给定算子A∈B（H1），B∈B（H2），以MD表示缺项2×2阶上三角算子矩阵

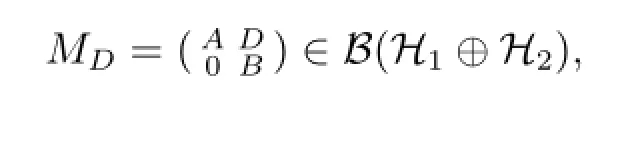
其中D∈B（H2，H1）待定.

经过近二十年的积累，2×2阶上三角算子矩阵的谱扰动研究已日臻完善，涌现出诸如谱，点谱，剩余谱，连续谱，近似点谱，亏谱，本质谱，Weyl谱，以及Browder谱等的扰动结果［2，3，5-8，10-18］.例如，文［15］研究了上三角算子矩阵MD的点谱和剩余谱扰动，得到如下结果

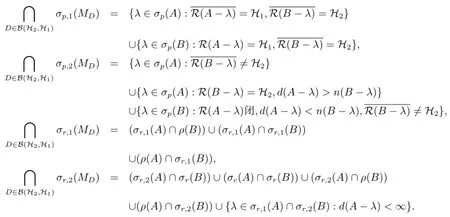
最近，文［4，18］分别研究了上三角算子矩阵MD，E，F的左（右）本质谱，以及点谱，剩余谱和连续谱的扰动；文［9］给出了MD，E，F的点谱，连续谱和剩余谱之并集的描述.本文在文［15］的基础上探讨了3×3阶情形，得到

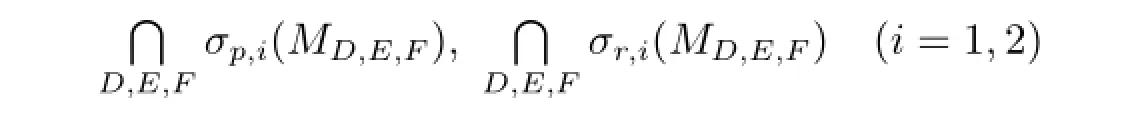
的完全描述.

对于有界算子T，分别以T∗，N（T）和R（T）表示T的共轭算子，零空间和值域；以n（T），d（T）分别表示N（T），N（T∗）的维数，即n（T）=dimN（T），d（T）=dimN（T∗）.下面给出文中涉及的一些基本概念和辅助引理.

定义1.1［1］设T为Banach空间X中的有界线性算子，则T的预解集ρ（T）定义为

ρ（T）=｛λ∈C：T-λ具有定义于X上的有界逆｝，并称集合σ（T）=Cρ（T）为T的谱.

由闭图象定理，λ∈ρ（T）当且仅当T-λ是双射.显然，σ（T）可分成下述互不相交的组成部分σ（T）=σp（T）∪σr（T）∪σc（T），其中

分别为T的点谱，剩余谱和连续谱.类似于文［1］，可对点谱和剩余谱进一步细分为

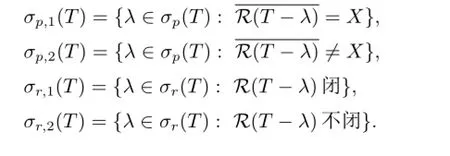
此外，称集合

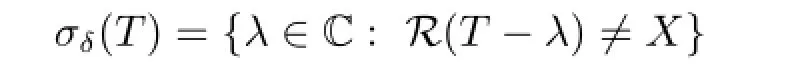
为T的亏谱.为叙述方便，记

如所熟知，λ∈ρm（T）当且仅当R（T-λ）闭；λ∈ρl（T）当且仅当T-λ为具有闭值域的单射.显然，σp，1（T）=σp（T）∩ρco（T），σp，2（T）=σp（T）∩σco（T），σr，1（T）=σr（T）∩ρm（T），σr，2（T）=σr（T）∩σm（T）.

引理1.1［9］设X，Y为Banach空间，T∈B（X，Y）.若R（T）不闭，则存在无穷维子空间使得

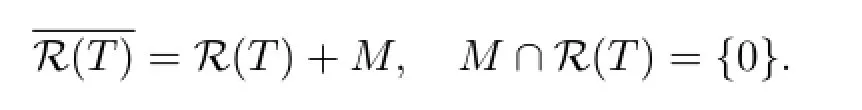
引理1.2设X，Y为Banach空间，T∈B（X，Y）.下述结论显然成立.

（i）若S∈B（X，Y）为有限秩算子，则R（T）闭当且仅当R（T+S）闭；

（ii）若U∈B（Y），V∈B（X）为可逆算子，则R（T）闭当且仅当R（UTV）闭.

引理1.3设A∈B（H1），B∈B（H2），C∈B（H3）为给定算子，则任给D，E，F均有λ∈ρin（MD，E，F）的充要条件为λ∈ρin（A）∩ρin（B）∩ρin（C）.

引理1.4设A∈B（H1），B∈B（H2），C∈B（H3）为给定算子，则任给D，E，F均有λ∈ρco（MD，E，F）的充要条件为λ∈ρco（A）∩ρco（B）∩ρco（C）.

引理1.1的证明见［9，推论1］；引理1.2是熟知的，引理1.3，1.4是显然的，证明从略.

2　主要结论及其证明

本节给出本文的主要结果和证明.为便于叙述，以下记

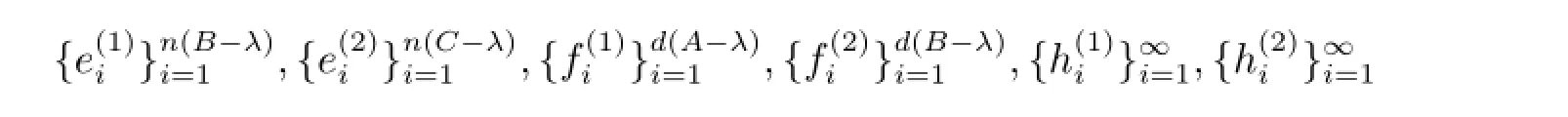
分别为N（B-λ），N（C-λ），R（A-λ）⊥，R（B-λ）⊥，H1，H2的规范正交基，其中A∈B（H1），B∈B（H2），C∈B（H3）.

定理2.1设A∈B（H1），B∈B（H2），C∈B（H3）为给定算子，则

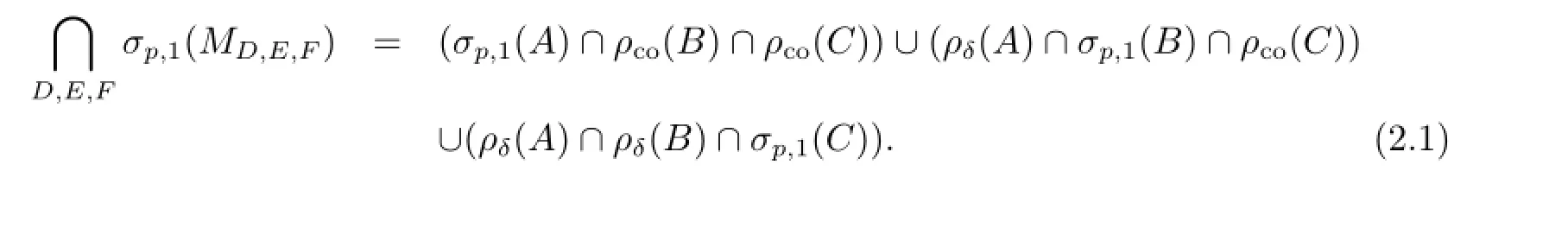
若λ∈Σ1，则λ∈σp（A），显然任给D，E，F均有λ∈σp（MD，E，F）.若λ∈Σ2Σ1，则λ∈ρ（A）∩σp，1（B）∩ρco（C），所以任给D，E，F均存在可逆算子V使得

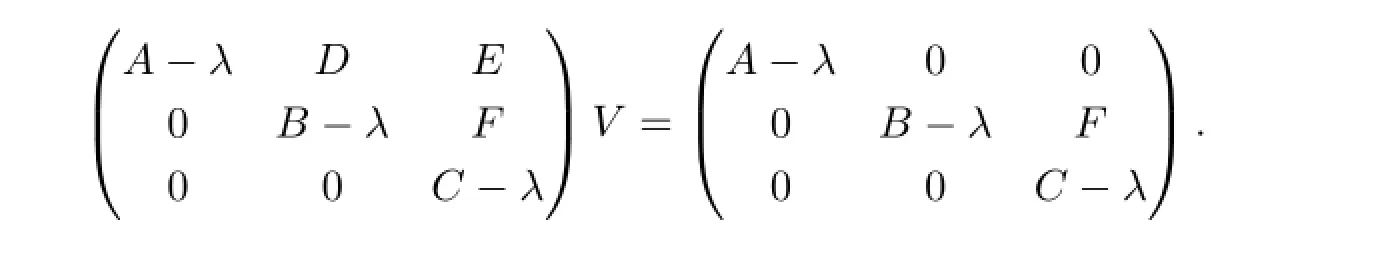
注意到λ∈σp（B）和V的可逆性，显然任给D，E，F均有λ∈σp（MD，E，F）.若λ∈Σ3（Σ1∪Σ2），则λ∈ρ（A）∩ρ（B）∩σp，1（C），同上讨论即可，不再赘述.

下面证明Σ⊂Σ1∪Σ2∪Σ3.为此，只须证若λ/∈Σ1∪Σ2∪Σ3必有λ/∈Σ，可分以下4种情形讨论.

情形1 λ∈σco（A）∪σco（B）∪σco（C）.此时，取D，E，F均为零算子，显然= H1⊕H2⊕H3，因此λ/∈Σ.

情形2 λ∈ρco（A）∩ρco（B）∩ρco（C）∩ρin（A）∩σm（A）.此时，由引理1.1，存在无穷维子空间M使得M∩R（A-λ）=｛0｝.记M的某个含有无穷多元素的规范正交集为.定义F=0，

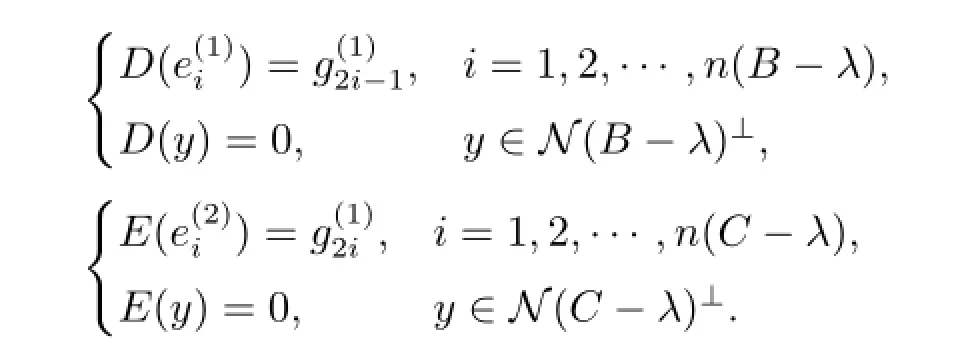
则MD，E，F-λ为单射，显然λ/∈Σ.

情形3 λ∈ρco（A∩ρco（C）∩ρin（A）∩ρin（B）∩σm（B）.此时，类似于情形2，存在无穷维子空间N⊂R（B-λ）使得N∩R（B-λ）=｛0｝.记N的某个含有无穷多元素的规范正交集为.取D，E均为零算子，并定义

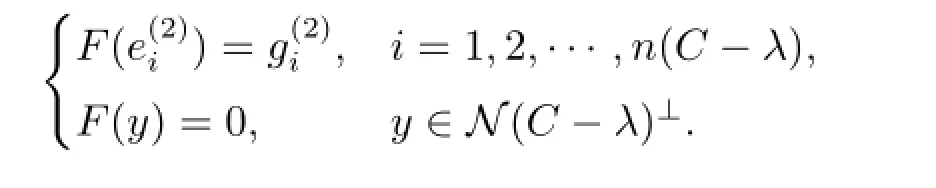
显然MD，E，F-λ为单射，因此λ/∈Σ.

情形4 λ∈ρco（A）∩ρco（B）∩ρco（C）∩ρin（A）∩ρin（B）∩ρin（C）.此时，由引理1.3，取D，E，F均为零算子便有MD，E，F-λ为单射，因此λ/∈Σ.

定理2.2设A∈B（H1），B∈B（H2），C∈B（H3）为给定算子，则

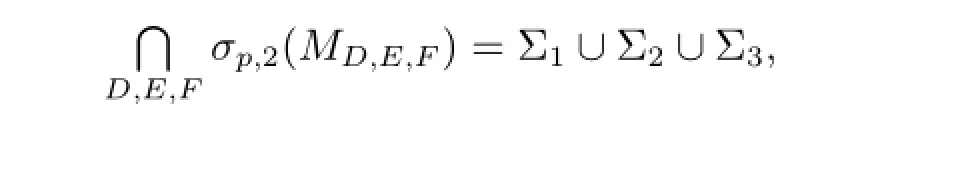
其中

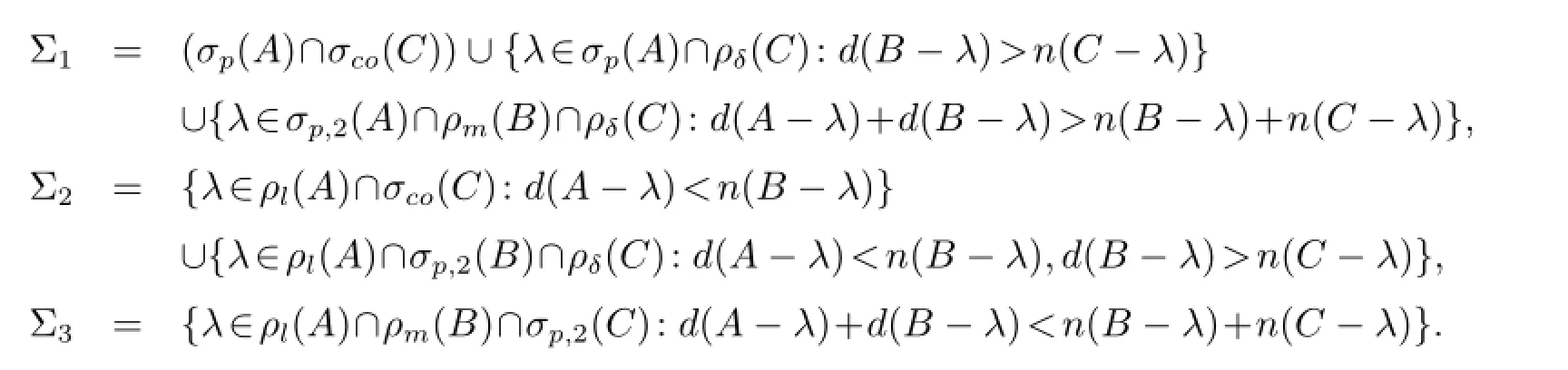
若λ∈Σ11，则λ∈σp（A）且/=H3.显然λ∈Σ.现设λ∈Σ12.由λ∈ρδ（C）可知任给D，E，F算子矩阵MD，E，F-λ均有如下分块表示

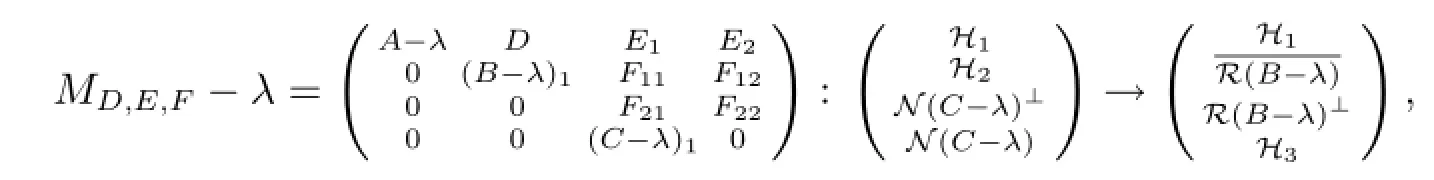
其中（C-λ）1为可逆算子.因此存在可逆算子U使得

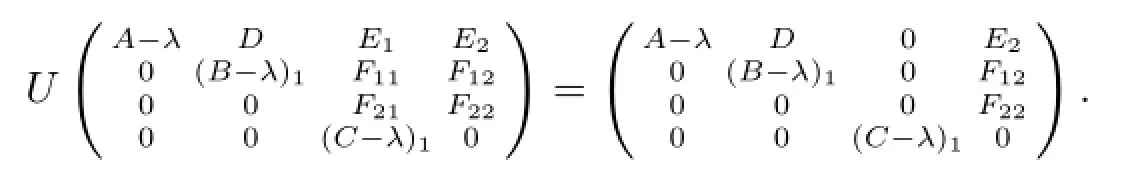
注意到d（B-λ）＞n（C-λ）可知无论如何选取D，E，F均有F22具有闭值域且不是满射，进而由U的可逆性得到λ∈σco（MD，E，F）.再由λ∈σp（A），显然λ∈Σ.以下假设λ∈Σ13.由于λ∈ρδ（C）∩ρm（B），所以任给D，E，F均有

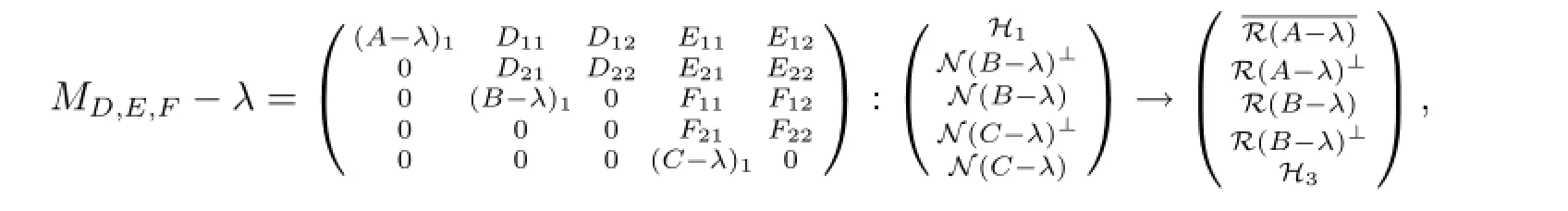
其中（B-λ）1，（C-λ）1为可逆算子.因此存在可逆算子U使得

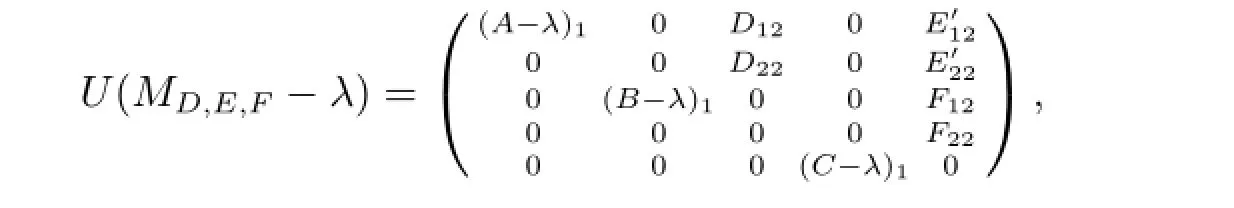
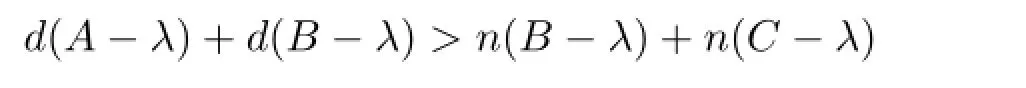
设λ∈Σ2.由于λ∈ρl（A），所以任给D，E，F均有

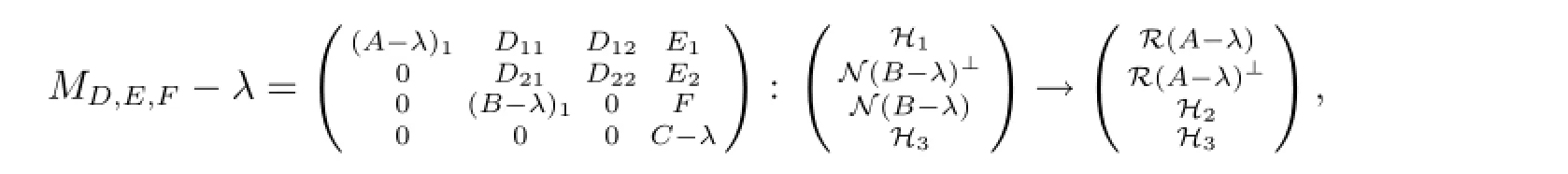
其中（A-λ）1为可逆算子.因此存在可逆算子V使得

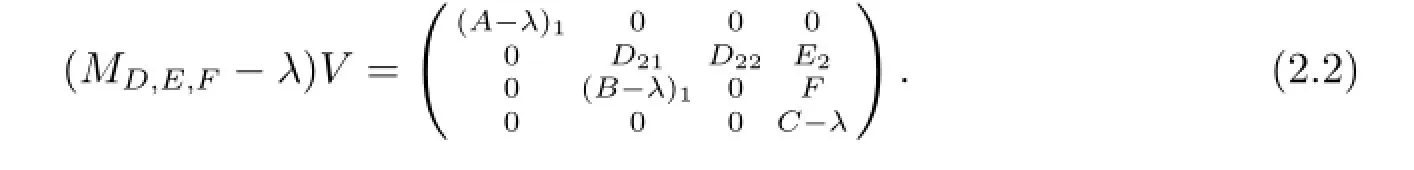
注意到n（B-λ）＞d（A-λ），显然无论如何选取D，E，F均有D22不是单射，进而由式（2.2）便知λ∈σp（MD，E，F）.这样，若λ∈σco（C），则任给D，E，F均有λ∈σco（MD，E，F），显然λ∈Σ；若λ∈ρδ（C）且d（B-λ）＞n（C-λ），则由Σ12的证明可知任给D，E，F均有λ∈σco（MD，E，F），从而λ∈Σ.于是Σ⊃Σ2.

现设λ∈Σ3.由λ∈ρl（A）∩ρm（B）可知任给D，E，F均有

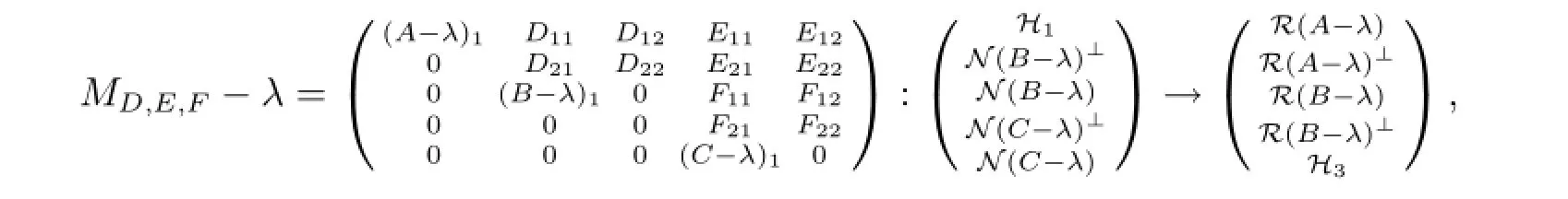
其中（A-λ）1，（B-λ）1均为可逆算子，（C-λ）1为单射.因此存在可逆算子U，V使得

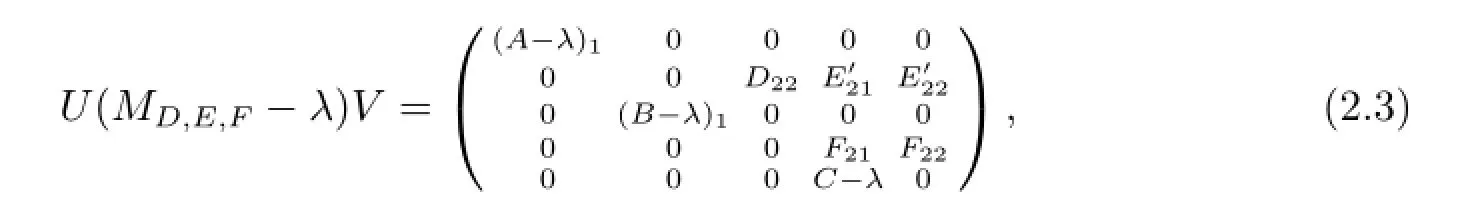
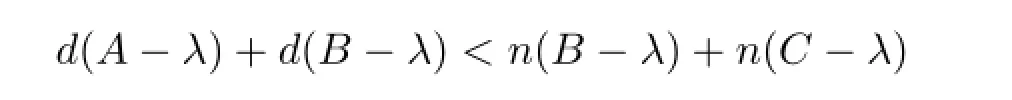
下面证明相反的包含关系.为此只须证若λ/∈Σ1∪Σ2∪Σ3必有λ/∈Σ，可分以下6种情形讨论.

情形1 λ∈ρin（A）∩σm（A）.此时，取定理2.1中情形2的D，E，F便有MD，E，F-λ为单射，因此λ/∈Σ.

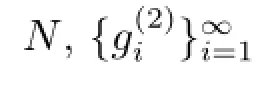
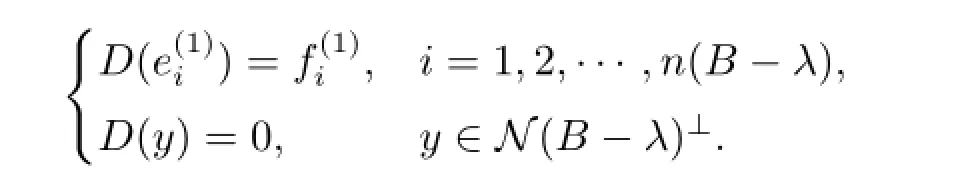
则MD，E，F-λ为单射，显然λ/∈Σ.

情形3 λ∈ρl（A）∩ρm（B），d（A-λ）≥n（B-λ）且d（A-λ）+d（B-λ）≥n（B-λ）+ n（C-λ）.此时，定义

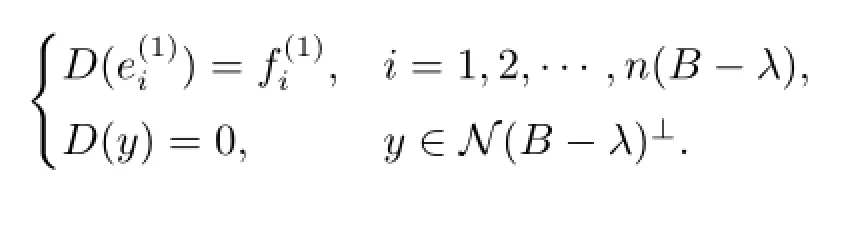
若d（B-λ）≥n（C-λ），则定义E=0，

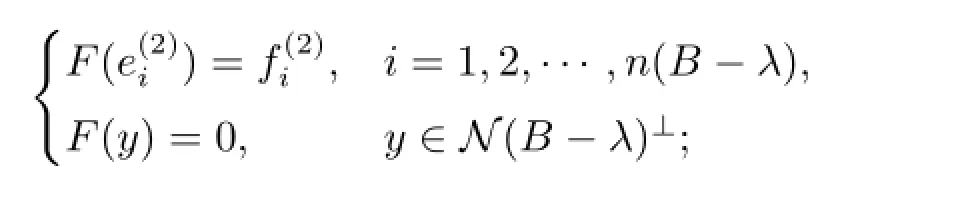
若d（B-λ）＜n（C-λ），由d（A-λ）+d（B-λ）≥n（B-λ）+n（C-λ）可知

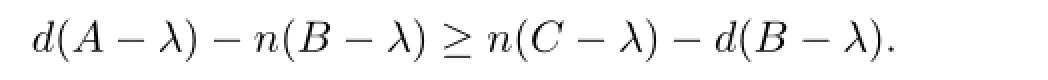
则定义

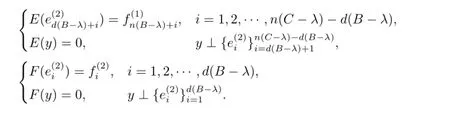
容易验证MD，E，F-λ为单射，显然λ/∈Σ.

情形4 λ∈ρco（C）∩σm（C）.此时，注意到λ∈σm（C）当且仅当.由引理1.1，存在无穷维子空间=N（C-λ）⊥使得=｛0｝.记Z的某个含有无穷多元素的规范正交集为.定义D=0，

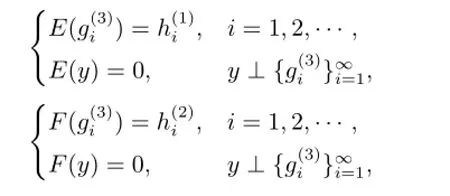
则E∗∈B（H1，H3），F∗∈B（H2，H3）均为单射，而且R（E∗）=R（F∗）=：i= 1，2，···｝.注意到=｛0｝和λ∈ρco（C），所以立即得到是单射.即 MD，E，F-λ具有稠值域，从而λ/∈Σ.

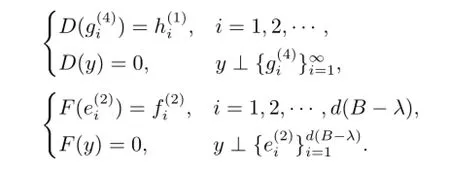
显然，MD，E，F-λ具有稠值域，因此λ/∈Σ.

情形6 λ∈ρm（B）∩ρδ（C），d（B-λ）≤n（C-λ）且d（A-λ）+d（B-λ）≤n（B-λ）+ n（C-λ）.此时，定义

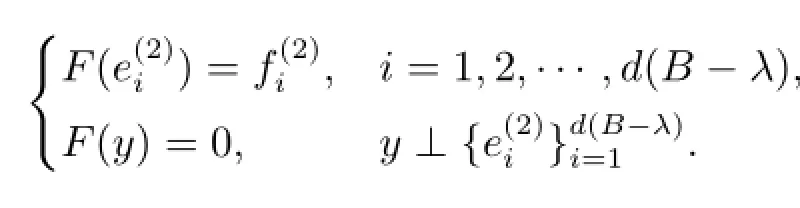
若d（A-λ）≤n（B-λ），则定义E=0，

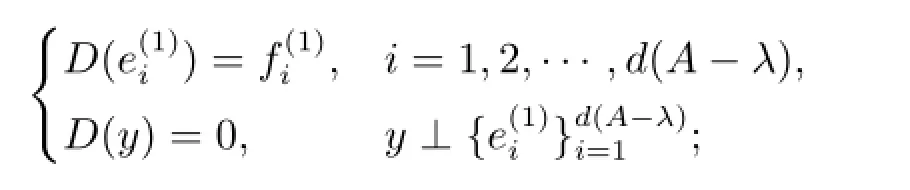
否则注意到d（A-λ）-n（B-λ）≤n（C-λ）-d（B-λ），定义

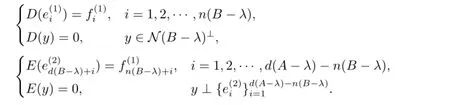
不难看出MD，E，F-λ是满射，从而λ/∈Σ.

定理2.3设A∈B（H1），B∈B（H2），C∈B（H3）为给定算子，则

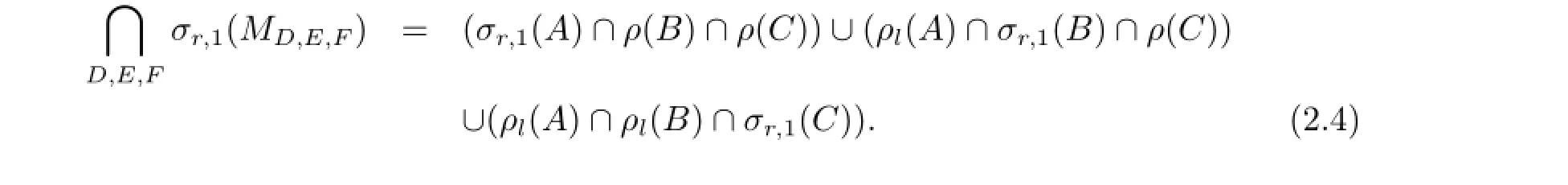
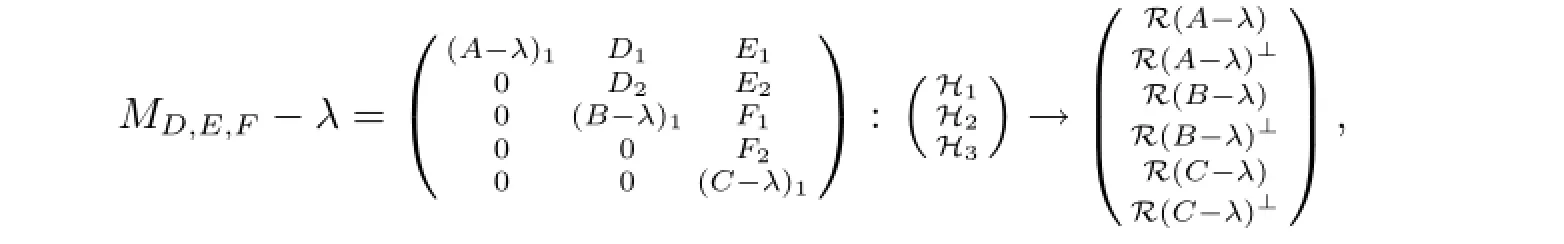
其中（A-λ）1，（B-λ）1，（C-λ）1均为可逆算子.因此存在可逆算子U使得

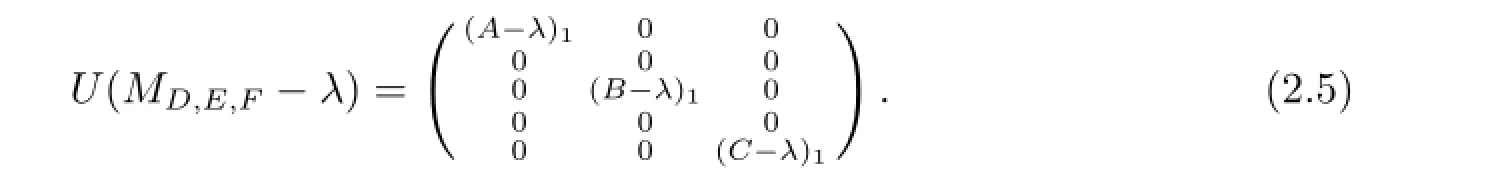
注意到d（A-λ），d（B-λ），d（C-λ）至少有一个大于零，由式（2.5）可知无论如何选取D，E，F均有MD，E，F-λ左可逆且R（MD，E，F-λ）/=H1⊕H2⊕H3.因此λ∈Σ.于是Σ⊃Σ1∪Σ2∪Σ3.

再证相反的包含关系.本文断言：λ∈Σ蕴含λ∈ρl（A）∩ρl（B）∩ρl（C）.若不然，取D，E，F皆为零算子便有λ∈σl（MD，E，F），这与λ∈Σ矛盾.因此只须证若λ∈（ρl（A）∩ρl（B）∩ρl（C））（Σ1∪Σ2∪Σ3）便有λ/∈Σ.这是显然的，因为λ∈Σ1∪Σ2∪Σ3蕴含λ∈ρl（A）∩ρl（B）∩ρl（C）且A-λ，B-λ，C-λ至少有一个值域不稠，从而若λ∈（ρl（A）∩ρl（B）∩ρl（C））（Σ1∪Σ2∪Σ3）便有λ∈ρ（A）∩ρ（B）∩ρ（C）.

定理2.4设A∈B（H1），B∈B（H2），C∈B（H3）为给定算子，则

其中

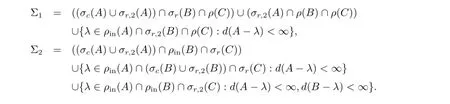
现记Σi的表达式中等号右端的集合依次为Σi1，Σi2，Σi3（i=1，2）.若λ∈Σ11∪Σ12∪Σ21，则必有λ∈σm（A）.显然任给D，E，F均有λ∈σm（MD，E，F）.若λ∈Σ13，则任给D，E，F均有

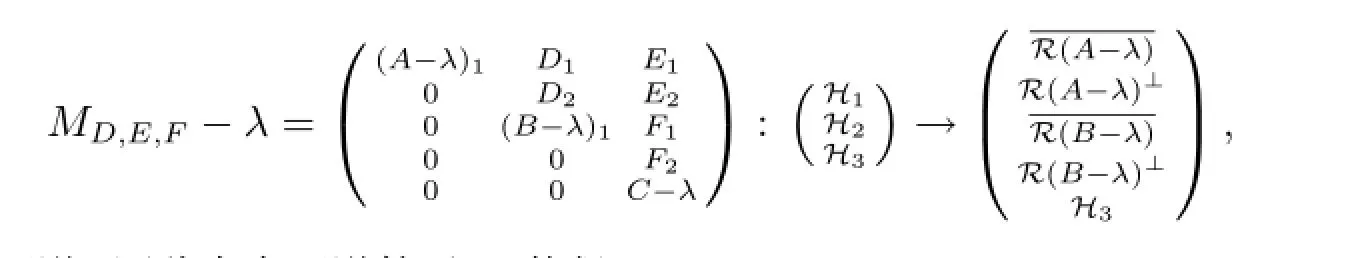
其中C-λ可逆.因此存在可逆算子U使得

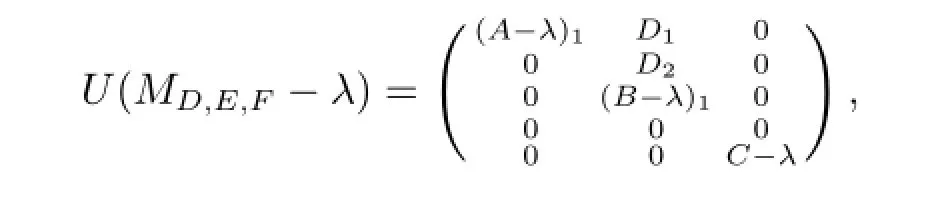
结合d（A-λ）＜∞，应用引理1.2可有λ∈σm（MD，E，F）当且仅当

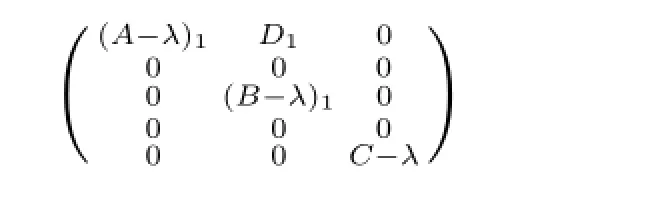
的值域不闭.这样若λ∈σm（A），同前述讨论可知，任给D，E，F均有λ∈σm（MD，E，F）；若λ/∈σm（A），则（A-λ）1为可逆算子，注意到λ∈σr，2（B）容易得到任给D，E，F均有λ∈σm（MD，E，F）.类似地，容易证明若λ∈Σ22∪Σ23，则任给D，E，F仍有λ∈σm（MD，E，F）.

再证Σ⊂Σ1∪Σ2.注意到任给D，E，F均有σr，2（MD，E，F）⊂σm（MD，E，F）.所以要证λ/∈Σ1∪Σ2蕴含λ/∈Σ，只须考虑如下3种情形即可.

情形1 λ∈σc（C），d（A-λ）＜∞且d（B-λ）＜∞.此时，注意到λ∈σm（C），取形如定理2.2中情形4的D，E，F可知MD，E，F-λ具有稠值域，显然λ/∈Σ.

情形2 λ∈σr，1（A）∩σc（B）∩ρ（C）且d（A-λ）＜∞.此时，取E，F均为零算子并定义，显然MD，E，F-λ具有稠值域，从而λ/∈Σ.

情形3 λ∈（ρ（A）∩σc（B）∩ρ（C））∪（σc（A）∩（ρ（B）∪σc（B））∩ρ（C））∪（σc（A）∩σc（B）∩ρ（C））.此时，取D，E，F均为零算子，显然MD，E，F-λ具有稠值域，因此λ/∈Σ.

注由上述定理，文［15］的结果可描述为

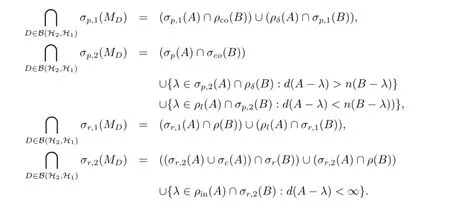
［1］Azizov T Ya，Iokhvidov I S.Linear operators in spaces with an indefinite metric［M］.Chichester：John Wiley&Sons Ltd.，1989.

［2］Cao X，Meng B.Essential approximate point spectra and Weyl's theorem for operator matrices［J］. J.Math.Anal.Appl.，2005，304：759-771.

［3］Cao X.Browder essential approximate point spectra and hypercyclicity for operator matrices［J］. Lin.Alg.Appl.，2007，426：317-324.

［4］曹小红.3×3阶上三角算子矩阵的Weyl型定理［J］.数学学报（中文版），2006，49：529-538.

［5］Djordjevi´c D S.Perturbations of spectra of operator matrices［J］.J.Oper.The.，2002，48：467-486.

［6］Djordjevi´c S V，Zguitti H.Essential point spectra of operator matrices through local spectral theory［J］.J.Math.Anal.Appl.，2008，338：285-291.

［7］Du H，Pan J.Perturbation of spectrums of 2×2 operator matrices［J］.Proc.Amer.Math.Soc.，1994，121：761-766.

［8］Hai G.，Chen A.On the right（left）invertible completions for operator matrices［J］.Integr.Equ. Oper.The.，2010，67：79-93.

［9］Hai G，Alatancang.Possible spectrums of 3×3 upper triangular operator matrices［J］.J.Math.Res. Expo.，2009，29：649-661.

［10］黄俊杰，阿拉坦仓，王华.上三角算子矩阵谱的自伴扰动［J］.数学学报（中文版），2010，53：1193-1200.

［11］Hwang I S，Lee W Y.The boundedness below of 2×2 upper triangular operator matrices［J］.Integr. Equ.Oper.The.，2001，39：267-276.

［12］Li Y，Du H.The intersection of essential approximate point spectra of operator matrices［J］.J.Math. Anal.Appl.，2006，323：1171-1183.

［13］Li Y，Sun X，Du H.The intersection of left（right）spectra of 2×2 upper triangular operator matrices［J］.Lin.Algebra Appl.，2006，418：112-121.

［14］Zerouali E H，Zguitti H.Perturbation of spectra of operator matrices and local spectral theory［J］. J.Math.Anal.Appl.，2006，324：992-1005.

［15］张澜，阿拉坦仓.一类缺项算子矩阵的谱扰动［J］.应用数学学报，2010，33：59-65.

［16］Zhang H，Du H.Browder spectra of upper-triangular operator matrices［J］.J.Math.Anal.Appl.，2006，323：700-707.

［17］Zhang S，Wu Z，Zhong H.Continuous spectrum，point spectrum and residual spectrum of operator matrices［J］.Lin.Algebra Appl.，2010，433：653-661.

［18］吴秀峰，黄俊杰，阿拉坦仓.三阶上三角算子矩阵点谱，连续谱和剩余谱的扰动［J］.数学学报，2015，35（3）：423-430.

PERTURBATION OF THE POINT AND RESIDUAL SPECTRA OF 3×3 UPPER TRIANGULAR OPERATOR MATRICES

HUANG Jun-jie，WU Xiu-feng，Alatancang
（School of Mathematical Sciences，Inner Mongolia University，Hohhot 010021，China）

The point and residual spectra of a bounded operator T are，respectively，split into σp，1（T），σp，2（T）and σr，1（T），σr，2（T），based on the denseness and closedness of its range. Let H1，H2，H3be infinite dimensional complex separable Hilbert spaces.Given the operators A∈B（H1），B∈B（H2）and C∈B（H3），some complete characterizations on the perturbations of the previous four spectra for the partial operator matrix MD，E，Fare given by means of the analysis method and block operator technique.

operator matrix；point spectrum；residual spectrum；perturbation

MR（2010）主题分类号：47A10；47A55O177.1；O177.7

A

0255-7797（2016）05-1056-11

2014-04-11接收日期：2014-06-23

国家自然科学基金资助（11461049；11371185）；内蒙古自治区自然科学基金资助（2013JQ01）.作者简介：黄俊杰（1977-），男，蒙古族，内蒙古兴安盟，教授，主要研究方向：算子矩阵理论及应用.

2010 MR Subject Classification：47A10；47A55