Existence of Solutions to Elliptic Equations with Variable Exponents and a Singular Term

CHEN XU-SHENG

(School of Mathematics,Jilin University,Changchun,130012)

Communicated by Gao Wen-jie



Existence of Solutions to Elliptic Equations with Variable Exponents and a Singular Term

CHEN XU-SHENG

(School of Mathematics,Jilin University,Changchun,130012)

Communicated by Gao Wen-jie

The purpose of this paper is to study a class of elliptic equations with variable exponents.By using the method of regularization and a priori estimates,we obtain the existence of weak solutions to these problems.

variable exponent,singular,existence

2010 MR subject classification:35J25,35J62

Document code:A

Article ID:1674-5647(2016)02-0185-08

1　Introduction

In this paper,we focus on the existence of solutions to the following quasi-linear elliptic equation

where Ω is a bounded domain in RN(N≥1)with smooth boundary∂Ω,f≥,/≡0,α≥1, p(x)is continuous in Ω satisfying

and the following logarithmic module of continuity condition

The p(x)-Laplace equation is naturally arisen in physical phenomenon,which could be used to describe the non-linear heat-exchanging problem,inhomogeneous material motionand image processing problem(see[1]–[4]).When p=2,the equation has been completely solved.When f∈Cβ(0＜β＜1),Lazer and Mckenna[5]declared that there exists a solution inif and only if α＜3,while for α＞1,the solution of the equation does not belong to C1(¯Ω).Boccardo and Orsina[6]discussed how the integrability of f and the value of α influence the existence,regularity and non-existence of the weak solutions.After Lazer’s results,Lair and Shaker[7]proved the existence of weak and classical solutions for semi-linear elliptic equations with general singular terms.

As to the quasi-linear case,Giacomoni et al.[8]considered the following equation

where 0＜ α＜1,p−1＜q≤p∗−1(p∗is the Sobolev conjugate exponent of p)and showed the existence and the multiplicity of the positive solutions.Later,Loc and Schmitt[9]improved the results under weaker assumptions.

To show the existence of such solutions,we combine the regularization method with a priori estimates to overcome the difficulties caused by the p(x)-Laplace operator and the singular term.

2　Main Result

We define some notations and introduce some elementary lemmas before stating and proving our main results,and the interested readers may refer to[10]for the proofs.

We denote by Lp(·)(Ω)the space of all measurable functions on Ω such that

This is a Banach space with respect to the Luxemburg norm

Lemma 2.1[10]For any u∈Lp(·)(Ω),

Lemma 2.2([10],H¨older’s inequality)For anyand

a.a.x∈Ω,q(x)satisfies

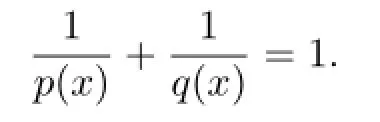
In order to prove the existence of the weak solution of(1.1),we consider the regularization problem as follows

where n∈N,fn(x)=min{f(x),n}.

Lemma 2.4For some fixed n∈N,f∈L1(Ω),(2.1)has the uniqueness non-negative solution

Proof.Fix n∈N.By using the theory of variation and the De Giorgi’s iteration,we know that for anythe following problem

Then we have

Lemma 2.5The solution sequence{un}of(2.1)is increasing in n.For any Ω′⊂⊂Ω, we have un＞0 in Ω′,and there exists a positive constant CΩ′(independent of n)such that for all n∈N the following holds

Proof.Since 0≤fn≤fn+1and α＞0,we have

Note that

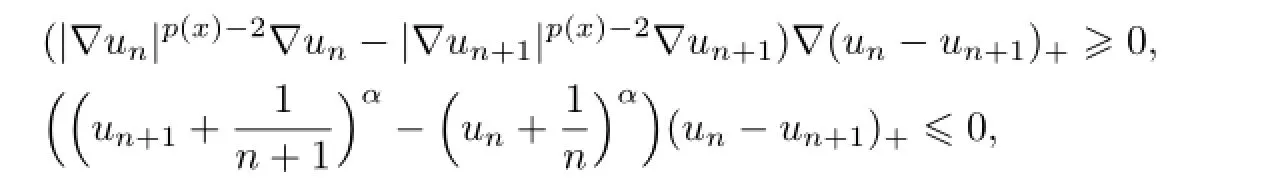
so we have

which implies

that is,for every n∈N,it holds that

Since the sequence{un}is increasing in n,we only need to prove(2.4)for u1.According to Lemma 2.4,we know the existence of a positive constant C with

Therefore,we have

Lemma 2.6Assume that there exists 0＜ β＜ 1 such that p(x)∈Cβ(¯Ω).Then the solution u1of(2.1)for n=1 satisfies

Proof.It is known from Theorem 1.2 in[12]that there exists 0＜γ＜1 such that u1∈Then the lemma can be proved by applying the arguments similar to those in[5], and the details are omitted.

With the preparation above,we are now going to prove the main result.

Theorem 2.1Suppose that f∈L1(Ω),f≥,/≡0 and α=1.Then(1.1)has a solution

Proof.Multiplying the first equation of(2.1)by unthen integrate over Ω,we have

By using Lemma 2.1 again,we can get

Therefore,there exist a subsequence of{un}(still denoted byandsuch that

where Ω′={x:φ/=0}.Therefore,the Lebesgue’s dominated convergence theorem gives us that

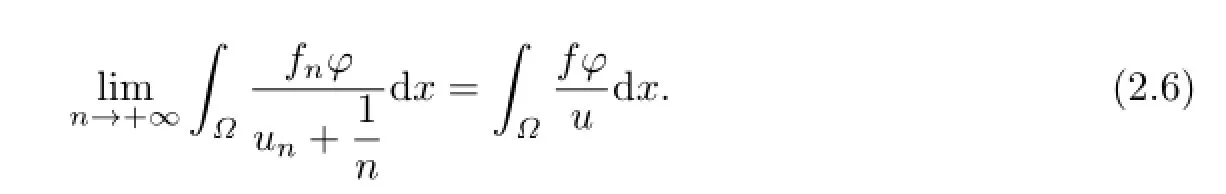
On the other hand,unsatisfies

Thus,by combining the above two equalities,we have

Then we need to prove

It is not hard to know that(2.7)and(2.8)hold for allwith compact support. Thus,choosing φ=(un−ξ)ζ,whereandwe have

Letting n→∞in(2.10)and recalling(2.8),we obtain

which implies that

Taking ξ=u−εψ in(2.11),where ψ is any function in W1,p(x)(Ω)and ε＞0 is a constant to yield∫

that is,

It follows by letting ε→0+that

Then,by the arbitrariness of ψ,we know that

Let ψ=ax,where a∈RNis any constant vector.Then the above equality becomes

which implies that

Thus we have shown that if f(x)∈L1(Ω),then u is the weak solution of(1.1).The proof is completed.

When α＞1,f needs to satisfy higher integrability to guarantee the existence of weak solution of(1.1).

Proof.Multiplying the first equation of(2.1)by unand integrating over Ω to get

Applying H¨older’s inequality to the right hand side of(2.13),recalling the monotonicity of {un}and Lemma 2.6,we have

Again by Lemma 2.1,we have

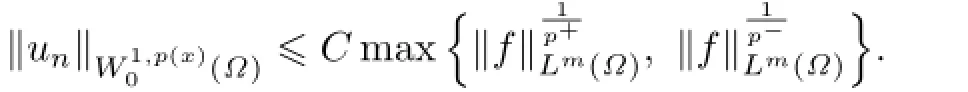
By the processes which are mostly the same to Theorem 2.1,we can prove the existence of solution to(1.1)in

[1]Acerbi E,Mingione G.Regularity results for stationary eletro-rheological fluids.Arch.Ration. Mech.Anal.,2002,164:213–359.

[2]Rajagopal K,Ruzicka M.Mathematical modelling of electro-rheological fluids.Contin.Mech. Thermodyn.,2001,13:59–78.

[3]Antontsev S N,Rodrigues J F.On stationary thermo-rheological viscous flows.Ann.Univ. Ferrara Sez.VII Sci.Mat.,2006,52:19–36.

[4]Chen Y,Levine S,Rao M.Variable exponent,linear growth functionals in image restoration. SIAM J.Appl.Math.,2006,66:1383–1406.

[5]Lazer A C,McKenna P J.On a singular nonlinear elliptic boundary value problems.Proc. Amer.Math.Soc.,1991,111:720–730.

[6]Boccardo L,Orsina L.Semilinear elliptic equations with singular nonlinearities.Calc.Var. Partial Differential Equations,2010,37:363–380.

[7]Lair A V,Shaker A W.Classical and weak solutions of a singular semilinear elliptic problem. J.Math.Anal.Appl.,1997,211(2):371–385.

[8]Giacomoni J,Schindler I,Tak´a˘c P.Sobolev versus H¨older local minimizers and existence of multiple solutions for a singular quasilinear equation.Ann.Sc.Norm.Super.Pisa Cl.Sci.(5), 2007,6:117–158.

[9]Loc N H,Schmitt K.Boundary value problems for singular elliptic equations.Rocky Mountain J.Math.,2011,41:555–572.

[10]Mih˘ailescu M,R˘adulescu V.On a nonhomogeneous quasilinear eigenvalue problem in Sobolev spaces with variable exponent.Proc.Amer.Math.Soc.,2007,135(9):2929–2937.

[11]Fan X L,Zhao Y Z,Zhang Q H.A strong maximum principle for p(x)-Laplace equations. Chinese Ann.Math.Ser.A,2003,24(4):495–500.

[12]Fan X L.Global C1,αregularity for variable exponent elliptic equations in divergence form.J. Differential Equations,2007,235(2):397–417.

10.13447/j.1674-5647.2016.02.11

date:July 1,2015.

E-mail address:chenxs@jlu.edu.cn(Chen X S).