Several Hermite-Hadamard Type Inequalities for Harmonically Convex Functions in the Second Sense with Applications

WANG WEN,YANG SHI-GUOAND LIU XUE-YING

(1.School of Mathematics and Statistics,Hefei Normal University,Hefei,230601)

(2.School of Mathematical Science,University of Science and Technology of China, Hefei,230026)

Communicated by Wang De-hui



Several Hermite-Hadamard Type Inequalities for Harmonically Convex Functions in the Second Sense with Applications

WANG WEN1,2,YANG SHI-GUO1AND LIU XUE-YING1

(1.School of Mathematics and Statistics,Hefei Normal University,Hefei,230601)

(2.School of Mathematical Science,University of Science and Technology of China, Hefei,230026)

Communicated by Wang De-hui

In this paper,we first introduce the concept“harmonically convex functions”in the second sense and establish several Hermite-Hadamard type inequalities for harmonically convex functions in the second sense.Finally,some applications to special mean are shown.

Hermite-Hadamard’s inequality,harmonically convex function,mean, inequality

2010 MR subject classification:26D15,26A51

Document code:A

Article ID:1674-5647(2016)02-0105-06

1　　Introduction

Throughout this paper,we let R=(−∞,+∞),R++=(0,+∞).We first recall some definitions of various convex functions.

Definition 1.1[1]–[2]A function f:I⊂R→R is said to be a convex function on I if

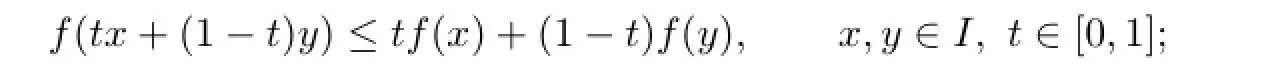
f is a concave function if−f is a convex function.

Definition 1.2[3]–[4]A function f:I⊂R{0}→R is said to be a harmonically convex function on I if

f is said to be a harmonically concave function if−f is a harmonically convex function.

Definition 1.3[5]A function f:I⊂R++→R++is said to be an m-AH convex function on I if

f is said to be an m-AH concave function if−f is an m-AH convex function.

Let f:I⊂R→R be a convex function.The following inequality is the well-known Hadamard’s inequality

We now recall some integral inequalities of Hermite-Hadamard type for some special functions.

Theorem 1.1[3]–[4]Let f:I⊂ R{0}→ R be a harmonically convex function,and a,b∈I with a＜b.If f∈L[a,b],then

For many recent results related to Hermite-Hadamard type inequalities,see[6]–[22].

The aim of this paper is first to introduce the concept“harmonically convex function”in the second sense and establish some Hermite-Hadamard type inequalities for harmonically convex functions in the second sense.Finally,some applications to special mean are shown.

2　　Definition and Lemma

The concept of harmonically convex function in the second sense can be introduced as follows.

Definition 2.1[20]A function f:I⊂R{0}→ R{0}is said to be a harmonically convex function in the second sense on I if

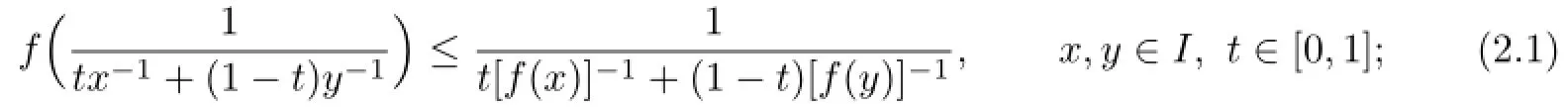
f is said to be a harmonically concave function in the second sense if−f is a harmonically convex function in the second sense.

Lemma 2.1Let f(x)=xr(x∈R++).If r≤0 or r≥1,then f(x)=xris a harmonically concave function in the second sense;If 0＜r＜1,then f(x)=xris a harmonically convex function in the second sense.

Proof.According to the properties of the function f(x)=xr(x∈R++),the following results is valid:

(1)For r≤0 or r≥1,f(x)=xris a convex function;

(2)For 0＜r＜1,f(x)=xris a concave function.

So,for x,y∈R++and t∈[0,1],we have

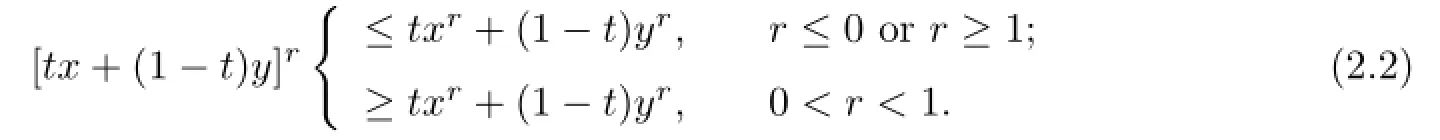
From(2.2),we get

By Definition 2.1 and using(2.3),it follows that Lemma 2.1 is valid.

3　　Main Results

Our main results are stated as follows.

Theorem 3.1Let f:I⊂R{0}→ R++be a harmonically convex function in the second sense,and a,b∈I with a＜b.If f∈L[a,b],then

Proof.Since f(x)is harmonically convex in the second sense,for all x,y∈I,we have

Further,by integrating for t∈[0,1]with respect to(3.3),we obtain

On the other hand,taking x=b and y=a in(2.1),we have

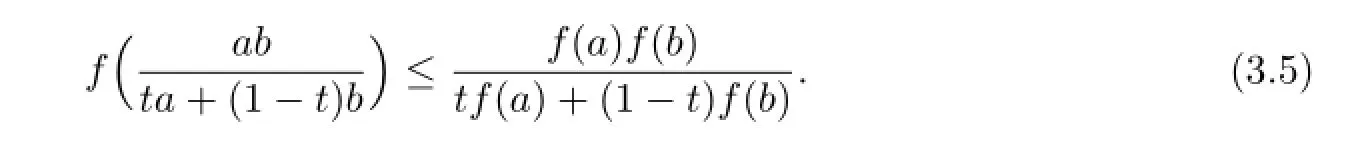
Further,by integrating for t∈[0,1],we obtain

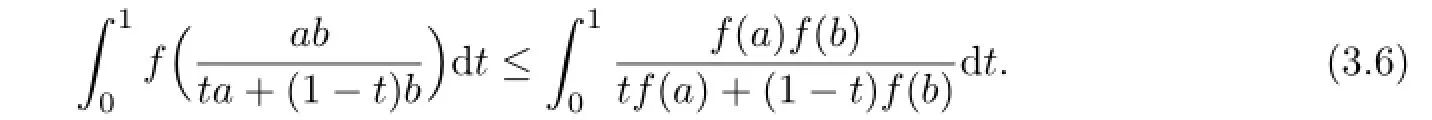
By computation we get

and

From(3.4)and(3.6)–(3.8),we obtain(3.1).

Corollary 3.1Let f:I⊂R{0}→ R++be a harmonically concave function in the second sense,and a,b∈I with a＜b.If f∈L[a,b],then

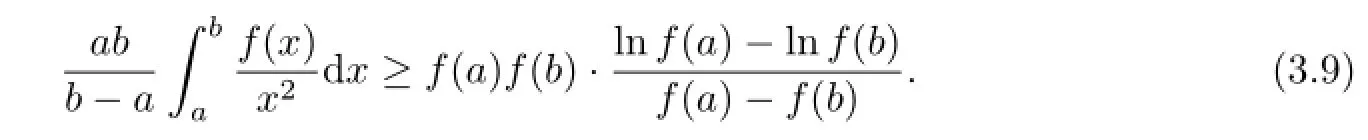
Proof.Since f(x)is harmonically concave in the second sense,inequalities(3.5)and(3.6) are reversed,and combining(3.7)and(3.8)we get(3.9).

Theorem 3.2Let f:I⊂R{0}→ R{0}be a harmonically convex function in the second sense,and a,b∈I with a＜b.If f∈L[a,b],then

Proof.Since f(x)is harmonically convex in the second sense,for all x,y∈I withwe have

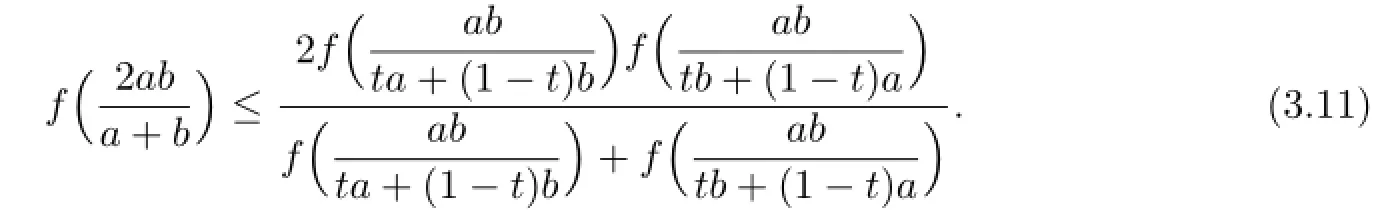
(3.11)can be written as

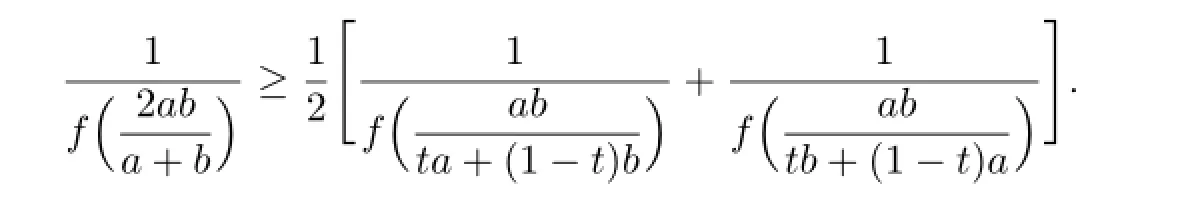
Further,by integrating for t∈[0,1],we obtain

Theorem 3.3Let f:I⊂R{0}→ R++be a harmonically convex function in the second sense,and a,b∈I with a＜b.If f∈L[a,b],then

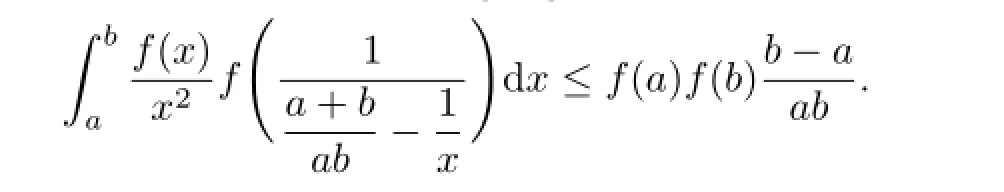
The proof is completed.

4　　Applications

Let I⊂R,a,b∈I with 0＜a＜b,and

Theorem 4.1Let a,b∈I,b＞a＞0 and 0≤r＜1.Then

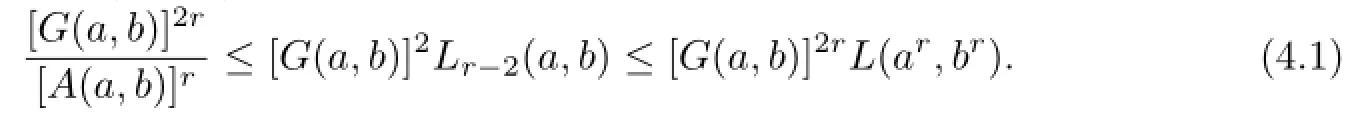
Proof.By Lemma 2.1 and Theorem 3.1,we get(4.1).

Theorem 4.2Let a,b∈I,b＞a＞0 and 0≥r or r＞1.Then

Proof.By Lemma 2.1 and Corollary 3.1,we get(4.2).

Theorem 4.3Let a,b∈I,b＞a＞0 and 0≤r≤1.Then

Proof.By Lemma 2.1 and Theorem 3.3,we obtain(4.3).

[1]Dragomir S S,Agarwal R P.Two inequalities for differentiable mappings and applications to special means of real numbers and to trapezoidal formula.Appl.Math.Lett.1998,5:91–95.

[2]Peˇcari´c J E,Proschan F,Tong Y L.Convex Functions,Partial Orderings and Statistical Applications.New York:Academic Press,1991.

[3]Iscan I.Hermite-Hadamard type inequalities for harmonically convex functions.Hacet.J. Math.Stat.,arXiv:1303.6089[math.CA].Submitted on 25 March 2013.

[4]Set E,Iscan I.Hermite-Hadamard type inequalities for harmaonically convex functions on the co-ordinates.arXiv:1404.6397v1[math.CA].Submitted on 25 April 2014.

[5]Zhang T Y,Qi F.Integral inequalities of Hermite-Hadamard type for m-AH convex functions. Turkish J.Anal.Number Theory,2014,2(3):60–64.

[6]Kirmaci U S.Inequalities for differentiable mappings and applications to special means of real numbers and to midpoint formula.Appl.Math.Comput.,2004,147:137–146.

[7]Iscan I,Wu S H.Hermite-Hadamard type inequalities for harmonically convex functions via fractional intergrals.Appl.Math.Comput.,2014,238:237–244.

[8]Iscan I.Hermite-Hadamard and Simpson-like type inequalities for differentiable harmonically convex functions.J.Math.,2014:Article ID 346305,10 pp.

[9]Kavurmaci H,Avci M,¨Odemir M E.New inequalities of Hermite-Hadamard type for convex functions with applications.arXiv:1006.1593vl[math.CA].Submitted on 1 Jan.2011.

[10]Avci M,Kavurmaci H,¨Odemir M E.New inequalities of Hermite-Hadamard type via s-convex functions in the second sense with applications.Appl.Math.Comput.,2011,217:5171–5176.

[11]Mevl¨ut T.Some integral inequalities for logarithmically convex functions.J.Egyptian Math. Soc.,2013.http://dx.doi.org/10.1016/j.joems.2013.07.004.

[12]¨Ozdemir M E.A theorem on mappings with bounded derivatives with applications to quadrature rules and means.Appl.Math.Comput.,2003,138:425–434.

[13]Tseng K L,Hwang S H,Dragomirc S S.New Hermite-Hadamard-type inequalities for convex functions(II).Comput.Math.Appl.,2011,62:401–418.

[14]Constantin P N.The Hermite-Hadamard inequality for log-convex functions.Nonlinear Anal., 2012,75:662–669.

[15]Wang W,Yang S G.Schur m-power convexity of a class of multiplicatively convex functions and applications.Abstr.Appl.Anal.,2014:Article ID 258108,12 pp.

[16]Kirmaci U S,et al.Hadamard-type inequalities for s-convex functions.Appl.Math.Comput., 2007,193:26–35.

[17]Dragomir S S.Hermite-Hadamard’s type inequalities for operator convex functions.Appl. Math.Comput.,2011,218:766–772.

[18]Shi H N.Theory of Majorization and Analytic Inequalities(in Chinese).Harbin:Harbin Institute of Technology Press,2013.

[19]Akdemir A O,¨Ozdemir M E,Varo˘sanec S.On some inequalities for h-convex functions.Math. Comput.Modelling,2012,55:746–753.

[20]Wu S H.Harmaonically convex functions and Jensen inequality(in Chinese).J.Sichuan Normal Univ.(Nat.Sci.),2004,27(4):382–386.

[21]Zhang T Y,He H,Ji A P.Some properties on harmonic convex function(in Chinese).J.Inner Mongolia Univ.Nationalities(Nat.Sci.),2006,21(4):361–363.

[22]Song Z Y.Hadamard inequality of harmonic average type for harmonic convex function(in Chinese).J.Hubei Polytech.Inst.,2011,14(1):105–108.

10.13447/j.1674-5647.2016.02.02

date:Dec.10,2014.

The Doctoral Programs Foundation(20113401110009)of Education Ministry of China, Natural Science Research Project(2012kj11)of Hefei Normal University,Universities Natural Science Foundation (KJ2013A220)of Anhui Province,and Research Project of Graduates Innovation Fund(2014yjs02).

E-mail address:wenwang1985@163.com(Wang W).