Multiple Solutions for the Eigenvalue Problem of Nonlinear Fractional Differential Equations

LIN XIAO-LI,LI HUI-LAI,*AND DAI QUN

(1.College of Mathematics,Jilin University,Changchun,130012)

(2.Institution of Science,Changchun University of Science and Technology,Changchun,130022)

Communicated by Wang Chun-peng



Multiple Solutions for the Eigenvalue Problem of Nonlinear Fractional Differential Equations

LIN XIAO-LI1,LI HUI-LAI1,*AND DAI QUN2

(1.College of Mathematics,Jilin University,Changchun,130012)

(2.Institution of Science,Changchun University of Science and Technology,Changchun,130022)

Communicated by Wang Chun-peng

In this article,multiple solutions for the eigenvalue problem of nonlinear fractional differential equation is considered.We obtain the existence and multiplicity results of positive solutions by using some fixed point theorems.

fraction differential equation,positive solution,fixed point,cone,eigenvalue problem

2010 MR subject classification:34B18

Document code:A

Article ID:1674-5647(2016)02-0173-12

1　Introduction

In this paper,we investigate the existence and multiplicity of positive solutions for eigenvalue problem of nonlinear fractional differential equations:

where 2＜α≤3 is a real number,is the Caputo derivative,λ is a positive parameter and a(t)∈C([0,1],[0,∞)),f(t,u)∈C([0,1]×[0,∞),[0,∞)).Firstly,we establish intervals of the parameter λ,which yield the conclusion that the problem(1.1)-(1.2)has a positive solution.Then we give some conditions about f(t,u),which also yield the existence of positive solutions using of fixed point theorem.At the end,by placing certain restrictions on the nonlinearity,we prove the existence of at least one,at least two,at least three,and infinitely many positive solutions of the problem(1.1)-(1.2)by applying some known fixed point theorems.

2　Preliminaries

Definition 2.1The Riemann-Liouville fractional integral of order α＞0 of a function f:(0,∞)→R is given by

provided that the right hand side is pointwise defined on(0,∞).

Definition 2.2The Caputo’s derivative of order α＞0 of a continuous function f: (0,∞)→R is given by

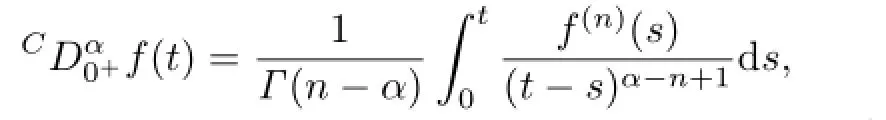
where n−1＜α≤n,provided that the right hand side is pointwise defined on(0,∞).

Lemma 2.1[10]Given f∈C([0,1]),and 2＜α≤3,the unique solution of

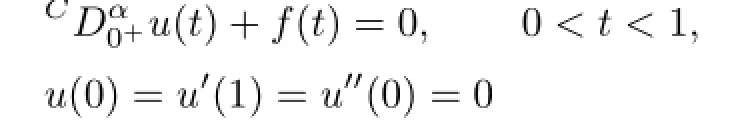
is

where

Proposition 2.1The Green’s function G(t,s)satisfies the following conditions:

(1)0＜G(t,s)≤G(1,s),t,s∈(0,1);

Lemma 2.2[11]Let X be a Banach space,K ⊆X is a cone,and Ω1,Ω2⊂K are two relatively non-empty open sets,Suppose that F:Ω2−→ K is a completely continuous operator such that either

(1)∥F(x)∥≤∥x∥,x∈∂Ω1;∥F(x)∥≥∥x∥,x∈∂Ω2,or

(2)∥F(x)∥≥∥x∥,x∈∂Ω1;∥F(x)∥≤∥x∥,x∈∂Ω2holds.Then F has a fixed point in¯Ω2Ω1.

Lemma 2.3[11]Let K be a cone in Banach space E.Suppose that T:is a completely continuous operator.

(i)If there exits a u0∈K{θ}such that u−Tu/=µu0for any u∈∂Krandµ≥0, then i(T,Kr,K)=0;

(ii)If Tu/=µu for any u∈∂Krandµ≥1,then i(T,Kr,K)=1.

Lemma 2.4[11]Let P be a cone in Banach space X.Suppose that T:P→P is a completely continuous operator.If there exists a bounded open set Ω(P)such that each solution of

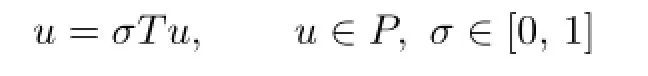
satisfies u∈Ω(P),then the fixed point index i(T,Ω(P),P)=1.

3　Main Results

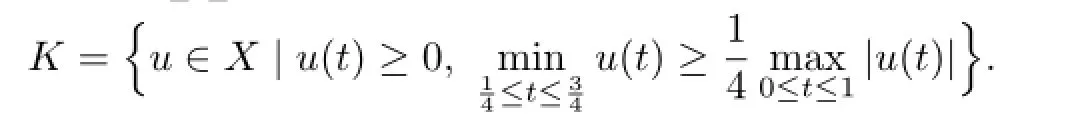
Define an operator T,

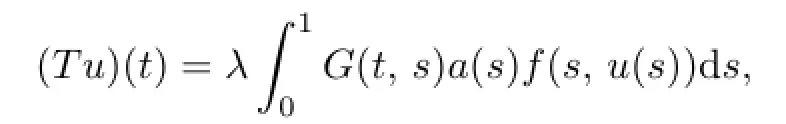
and a(t)∈C([0,1],[0,∞)),f(t,u)∈C([0,1]×[0,∞),[0,∞)).So T:K → K is a completely operator.

Let

We assume the following conditions hold:

(A1)a(t)∈C([0,1],[0,∞)),a(t)/=0;

(A2)f(t,u)∈C([0,1]×[0,∞),[0,∞)),and there exists a g∈C([0,∞),[0,∞))such that

Set

Obviously,L1,L2are completely continuous linear operators,and L1(P)⊂K,L2(P)⊂K. By virtue of the Krein-Ruman theorem and Proposition 2.1,we have the following lemma.

Lemma 3.1Assume that(A1)and(A2)hold.Then the spectral radius r(L1)＞ 0, r(L2)＞0 and L1,L2respectively have a positive eigenfunction ϕ1,ϕ2corresponding to its first eigenvalue λ1=(r(L1))−1,λ2=(r(L2))−1,that is,ϕ1=λ1L1ϕ1,ϕ2=λ2L2ϕ2.

It is clear that L1(ϕ1)⊂K,L2(ϕ2)⊂K.So ϕ1∈K,ϕ2∈K.

For convenience,we introduce the following notations:

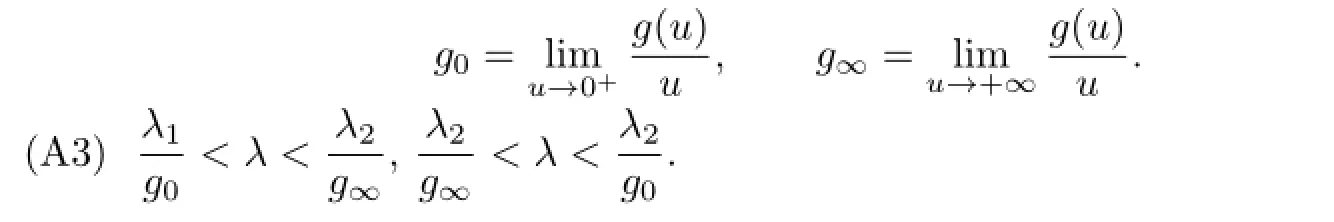
Theorem 3.1Suppose that(A1),(A2)and(A3)hold.Then the problem(1.1)-(1.2)has at least one positive solution.

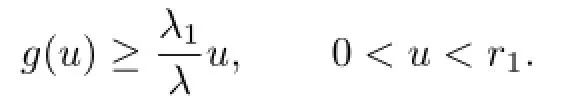
Then,for u∈∂Kr1,we have

By Lemma 3.1,we have

Assume that there is no fixed point on∂Kr1(otherwise,the proof is finished).Now we show that

where ψ1∈K{θ}and ψ1is not the first eigenfunction of L1.Suppose that u−Tu=µψ1held,then there would exist u1∈∂Kr1andµ1＞0 such that

Let

Then

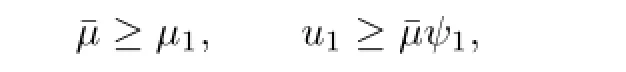
and

Thus

which contradicts the definition of¯µ.So(3.1)is true.By Lemma 2.3,we have

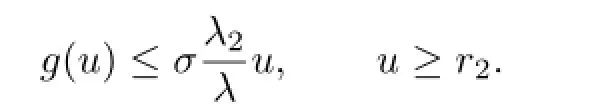
Let

Then L:C[0,1]→C[0,1]is a bounded linear operator and L(K)⊂K.Denote

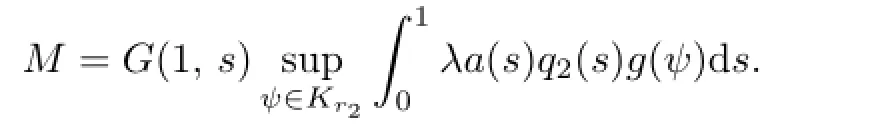
It is clear that M＜+∞.

Let

We proof that W is bounded.For any ψ∈W,set

and denote

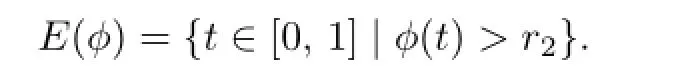
Then

Thus,

Since λ2is the first eigenvalue of L2,and for 0＜σ＜1,σλ2L2ψ=Lψ,so(r(L))−1＞1, the inverse operator(I−L)−1exists and

It follows from L(K)⊂K that(I−L)−1(K)⊂K.So we have

and W is bounded.

Choose r3＞max{r2,∥(I−L)−1M∥}.Then,by Lemma 2.4,we have

Since

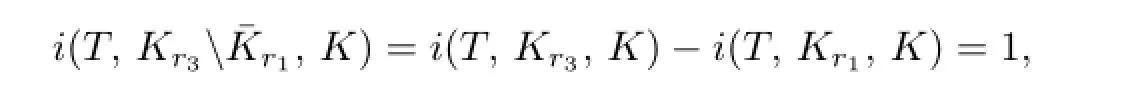
it is easy to know that T has at least one fixed point on¯Kr3Kr1.That is to say,the problem(1.1)–(1.2)has at least one positive solution.

In the following,we give some results under some conditions concerning the function f(t,u).

Define

Assume that

(B1)f0=∞,f∝=∞.

(B2)There exists a p＞0 such that for 0＜u＜p,f(t,u)＜Kp,and

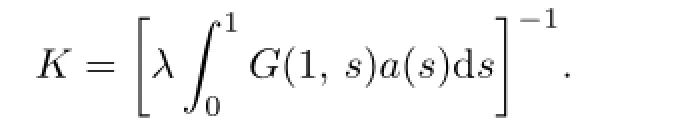
Theorem 3.2Assume that(B1)and(B2)hold.Then the problem(1.1)-(1.2)has at least two positive solutions.

Let

For u∈K∩∂Ωr,we have

Thus

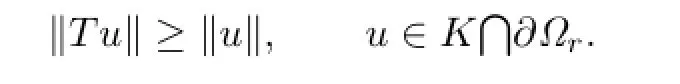
Let

Thus

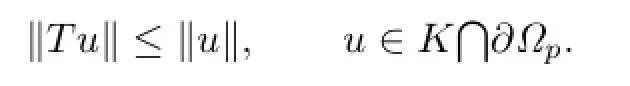
On the other hand,by(B1)f∝=∞,we know that there exists a positive number M∗such that for any u＞4M∗,

where ρ satisfies

Let

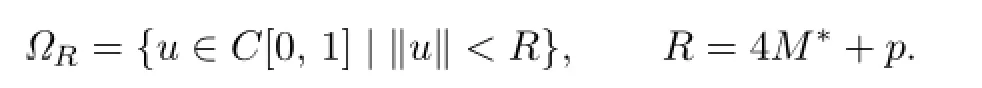
Thus

Therefore,the problem(1.1)-(1.2)has at least two positive solutions u1,u2satisfying

Corollary 3.1Assume that the following conditions hold:

(B3)f0=0,f∝=0;

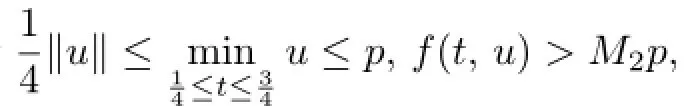
Then the problem(1.1)–(1.2)has at least two positive solutions.

Proof.The proof is similar to that of Theorem 3.2 and hence is omitted here.

Corollary 3.2Assume that f0=0,f∝=∞hold.Then the problem(1.1)-(1.2)has at least one positive solution.

Corollary 3.3Assume that f0=∞,f∝=0 hold.Then the problem(1.1)-(1.2)has at least one positive solution.

In the following discussions we need the constants

For the forthcoming analysis,we need the following assumptions:

(C1)There exists a p＞0 such that f(t,u)≤kp for t∈[0,1]and 0≤u≤p.

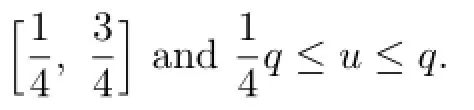
Theorem 3.3Assume that there exists positive numbers p/=q such that the condition (C1)is satisfied with respect to p,(C2)is satisfied with respect to q.Then the problem (1.1)-(1.2)has a positive solution u with p≤∥u∥＜q.

Proof.Without loss of generality,we assume that 0＜p＜q.Define the open sets

Thus

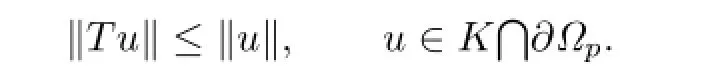
Thus

By Lemma 2.2,we know that there exists one fixed point on∩which means that the problem(1.1)–(1.2)has a positive solution u,and p≤∥u∥＜q.

Theorem 3.4If either

holds,where k,m,f0and f∝are as previously defined,then the problem(1.1)-(1.2)has a positive solution.

Proof.Assume that(C3)holds.Then there exist a sufficiently small p＞0 and a sufficiently large q＞0 such that

and

Then

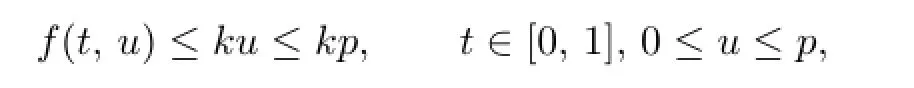
and

In particular,both(C1)and(C2)hold.By Theorem 3.3,we know that the problem (1.1)-(1.2)has a positive solution.

Now we assume that(C4)holds.Then there exist 0＜p＜q such that

From(3.2)we have

Now we consider(3.3)and discuss two cases.

Case 1.Assume that there exists an N＞0 such that

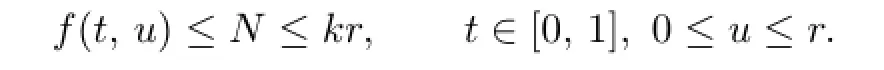
Thus(C1)is satisfied with respect to r.

Case 2.Assume that f is unbounded.Then there exist t0∈[0,1]andsuch that

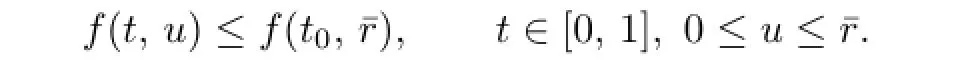
Then

and(C1)is satisfied with respect to¯r.

Thus in both cases condition(C1)is satisfied,Theorem 3.3 yields the conclusion.

Theorem 3.5Assume that(C1)is satisfied for some p＞0 and,in addition,

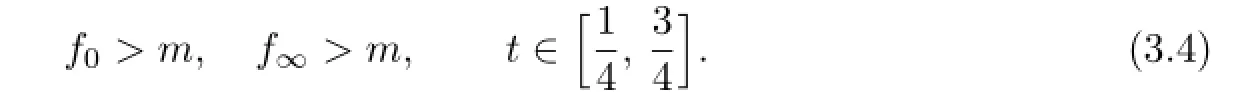
Then the problem(1.1)-(1.2)has at least two positive solutions u1,u2,and 0＜∥u1∥＜p＜∥u2∥.

Proof.Similar to the proof of Theorem 3.4,there exist 0＜p1＜p＜p2such that

and

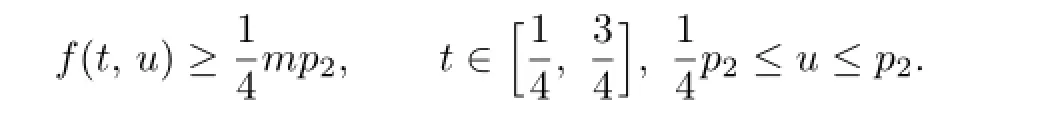
By Theorem 3.3,we know that there exist two solutions u1and u2of the problem(1.1)–(1.2) and 0＜p1＜∥u1∥＜p＜∥u2∥＜p2.

In a completely analogous manner,the following result is also obtained.

Theorem 3.6Assume that(C2)is satisfied for some q＞0 and,in addition,

Then the problem(1.1)-(1.2)has at least two positive solutions u1,u2and 0＜∥u1∥＜q＜∥u2∥.

Now we state a result for the existence of at least three positive solutions.

Corollary 3.4Assume that(C3)(or resp.,(C4))is satisfied,and suppose that there exist 0＜p1＜p2such that(C1)holds with respect to p=p2(resp.,p=p1),and(C2)holds respect to q=p1(resp.,q=p2).Then the problem(1.1)-(1.2)has at least three positive solutions u1,u2and u3satisfying 0＜∥u1∥＜p1＜∥u2∥＜p2＜∥u3∥.

In the following we state some sufficient conditions which yield the result about n positive solutions of the problem(1.1)-(1.2).

Corollary 3.5Let n=2j+1,where j is an integer.Assume that(C3)(or resp.,(C4)) is satisfied,and suppose that there exist 0＜p1＜···＜pn−1such that(C2)(resp.,(C1)) holds with respect to p2i−1,1≤i≤j,and(C1)(resp.,(C2))holds respect to p2i,1≤i≤j. Then the problem(1.1)-(1.2)has at least n positive solutions u1,u2,···,unand 0＜∥u1∥＜p1＜∥u2∥＜···＜∥un−1∥＜pn−1＜∥un∥.

Proof.By(C3)f0＜k,there exists an r∈(0,p1)such that

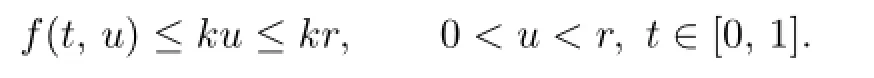
By(C1),we have

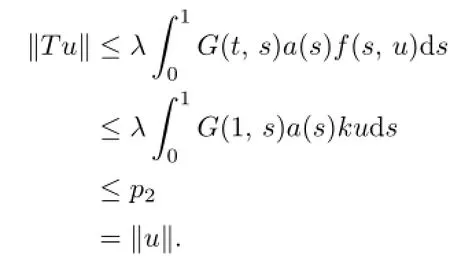
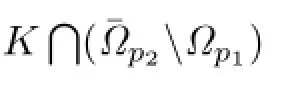
Furthermore,in the same way,we can get n positive solutions.

Corollary 3.6Let n=2j,where j is an integer.Assume that(C3)(or resp.,(C4))is satisfied,and suppose that there exist 0＜p1＜ ···＜pn−1such that(C1)(resp.,(C2)) holds with respect to p2i,1≤i≤j,and(C2)(resp.,(C1))holds with respect to p2i−1, 1≤i≤j−1.Then the problem(1.1)-(1.2)has at least n positive solutions u1,u2,···,un, and 0＜∥u1∥＜p1＜∥u2∥＜···＜∥un−1∥＜pn−1＜∥un∥.

[1]Anderson D R.Multiple solutions and eigenvalues for third-order right focal boundary value problems.J.Math.Anal.Appl.,2002,276:135–157.

[2]Miller K S,Ross B.An Introduction to the Fractional Calculus and Fractional Differential Equations.New York:Wiley,1993.

[3]Podlubny I.Fractional Differential Equations,Mathematics in Science and Engineering.New York:Academic Press,1999.

[4]Zhang J,Xu C.Trust region dogleg path algorithms for unconstrained minimization.Ann. Oper.Res.,1999,87:407–418.

[5]El-sayed A M A.Nonlinear functional differential equations of arbitrary order.Nonlinear Anal., 1998,33:181–186.

[6]Samko S G,Kilbas A A,Marichev O I.Fractional Integrals and Derivatives,Theory and Applications.Yverdon:Gordon and Breach,1993.

[7]Lakshmikantham V,Vatsala A S.Theory of fractional differential inequalities and applications. Commun.Appl.Anal.,2007,11:395–402.

[8]Lakshmikantham V,Vatsala A S.Basic theory of fractional differential equations.Nonlinear Anal.TMA,2008,69:2677–2682.

[9]Lakshmikantham V,Vatsala A S.General uniqueness and monotone iterative technique for fractional differential equations.Appl.Math.Lett.,2008,21:828–834.

[10]Bai Z B,Qiu T T.Existence of positive solution for singular fractional differential equation. Appl.Math.Comput.,2009,215:2761–2767.

[11]Krasnoselskii M A.Positive Solutions of Operator Equations.Groningen:P.Noordhoff Ltd., 1964.

[12]Wang Y Q,Liu L Y,Wu Y H.Positive solutions for a nonlocal fractional differential equation. Nonlinear Anal.,2011,74:3599–3605.

[13]Han X L,Gao H L.Existence of positive solutions for eigenvalue problem of nonlinear fractional differential equation.Adv.Difference Equ.,2012,66:1–8.

10.13447/j.1674-5647.2016.02.10

date:March 9,2015.

The NSF(10771085)of China.

.

E-mail address:linxl13@mails.jlu.edu.cn(Lin X L),lihuilai@jlu.edu.cn(Li H L).