A Note on General Third Geometric-arithmetic Index of Special Chemical Molecular Structures

GAO WEI

(School of Information Science and Technology,Yunnan Normal University,Kunming,650500)

Communicated by Du Xian-kun



A Note on General Third Geometric-arithmetic Index of Special Chemical Molecular Structures

GAO WEI

(School of Information Science and Technology,Yunnan Normal University,Kunming,650500)

Communicated by Du Xian-kun

In theoretical chemistry,the geometric-arithmetic indices were introduced to measure the stability of alkanes and the strain energy of cycloalkanes.In this note, we report the general third geometric-arithmetic index of unilateral polyomino chain and unilateral hexagonal chain.Also,the third geometric-arithmetic index of these chemical structures are presented.

molecular graph,general third geometric-arithmetic index,unilateral polyomino chain,unilateral hexagonal chain

2010 MR subject classification:05C15

Document code:A

Article ID:1674-5647(2016)02-0131-11

1　Introduction

One of the most important applications of chemical graph theory is to measure chemical, physical and pharmaceutical properties of molecules called alkanes.Several indices relied on the graphical structure of the alkanes are defined and employed to model both the melting point and boiling point of the molecules.Molecular graph is a topological representation of a molecule such that each vertex represents an atom of molecule,and covalent bounds between atoms are represented by edges between the corresponding vertices.

Specifically,topological index can be regarded as a score function f:G→R+with this property that f(G1)=f(G2)if two molecular graphs G1and G2are isomorphic.There are several vertex distance-based and degree-based indices which are introduced to analyze the chemical properties of molecule graph.For instance,Wiener index,PI index,Szeged index, atom-bond connectivity index and geometric-arithmetic index.Several papers contributedto determine the indices of special molecular graphs(see[1]–[9]).

All(molecular)graphs considered in this paper are finite,loopless,and without multiple edges.Let G be a(molecular)graph with vertex set V(G)and edge set E(G).All graph notations and terminologies used but undefined in this paper can be found in[10].

By considering the degrees of vertices in G,Vukicevic and Furtula[11]developed the geometric-arithmetic index,shortly GA index,which is defined by

where d(u)denotes the degree of vertex u∈V(G).

Yuan et al.[12]obtained the lower and upper bounds for GA index of molecular graphs in terms of the numbers of vertices and edges.They also determined the n-vertex molecular trees with the minimum,the second and the third minimum,as well as the second and the third maximum GA indices.Das et al.[13]obtained the lower and upper bounds on GA indices and characterize molecular graphs for which these bounds are best possible. Moreover,they discussed the effect on GA index of inserting an edge into a molecular graph. Madanshekaf and Moradi[14]calculated the geometric-arithmetic index of two infinite classes of dendrimers.

Fath-Tabar et al.[15]defined a new version of the geometric-arithmetic index,i.e.,the second geometric-arithmetic index:

where n(u)is the number of vertices closer to vertex u than vertex v and n(v)defines similarly.In[16],the maximum and the minimum second geometric-arithmetic index of the star-like tree are learned in view of an increasing or decreasing transformation of the second geometric arithmetic index of trees.Furthermore,they determine the corresponding extremal trees.

Let e=uv be an edge of the molecular graph G.The number of edges of G whose distance to the vertex u is smaller than the distance to the vertex v is denoted by mu(e). Analogously,mv(e)is the number of edges of G whose distance to the vertex v is smaller than the distance to the vertex u.Zhou et al.[17]proposed a third class of geometric-arithmetic index:

For more chemical engineering applications,the extension version of geometric-arithmetic indices are given by researches.Eliasi and Iranmanesh[18]defined the ordinary geometricarithmetic index(or,general geometric-arithmetic index)as follows:

where γ is a real number.For a real number γ,the general second geometric-arithmeticindex is given by

In this note,we expand the third geometric-arithmetic index,and raise the general geometric-arithmetic index as

where γ is a real number.

Although there have been several advances in geometric-arithmetic index and second geometric-arithmetic index of molecular graphs,the study of third geometric-arithmetic index of special chemical structures has been largely limited.In addition,as widespread and critical chemical structures,polyomino system and hexagonal system are widely used in medical science and pharmaceutical field.As an example,polyomino chain is one of the basic chemical structures,and exists widely in benzene and alkali molecular structures.For these reasons,we have attracted tremendous academic and industrial interests to research the third geometric-arithmetic index and its general version of these molecular structure from a mathematical point of view.

The contributions of our note are two-fold.First,we compute the general third geometricarithmetic index of unilateral polyomino chain.Then,the general third geometric-arithmetic index of unilateral hexagonal chain is calculated.

2　General Third Geometric-arithmetic Index of Polyomino Chain

From the view of graph theory,polyomino is a finite 2-connected planar graph and each interior face is surrounded by a square with length 4.Polyomino chain is one class of polyomino such that the connection of centres for adjacent squares constitute a path c1c2···cn,where ciis the centre of i-th square.Polyomino chainis called a linear chain if the subgraph induced by all 3-degree vertices is a graph with n−2 squares.Furthermore,polyomino chainis called a Zig-zag chain if the subgraph induced by all vertices with degree＞2 is path with n−1 edges.In what follows,we useandto denote linear polyomino chain and Zig-zag polyomino chain,respectively.The structure ofandcan refer to Fig.2.1.

Fig.2.1　The structure ofand

Use the similar technology raised in[8]and[19]–[20],the terminology of elementary cut described as follows.Choose an edge e of the polyomino system and draw a straight line through the center of e,orthogonal on e.This line will intersect the perimeter in two end points P1and P2.The straight line segment C whose end points are P1and P2is the elementary cut,intersecting the edge e.A fragment S in polyomino chain is just maximal linear chain which includes the squares in start and end vertices.Let l(S)be the length of fragment which denotes the number of squares it is contained.Letbe a polyomino chain with n squares and consist of fragment sequence S1,S2,···,Sm(m≥1).Denote l(Si)=li(i=1,···,m).It is not difficult to verify that l1+l2+···+lm=n+m−1 andFor the k-th fragment of polyomino chain,the cut of this fragment is the cut which intersects with lk+1 parallel edges of squares in this fragment. A fragment is called horizontal fragment if its cut parallels to the horizontal direction,and called vertical fragment if its cut parallels to the vertical direction.Unilateral polyomino chain is a special kind of polyomino chain such that for each vertical fragment,two horizontal fragments(if exists)adjacent it appear in the left and right sides,respectively.

Fig.2.2　I-type cut and II-type cut of unilateral polyomino chain

Case 1.Edge e is I-type in j-th square of k-th fragment(i.e.,e is edge which is passed by dotted line in Fig.2.2).

For this case,we observe that there lk+1 such edges in k-th fragment.Then,we have

and

Case 2.Edge e is II-type in j-th square of k-th fragment(i.e.,e is edge which is passed by real line in Fig.2.2).

For this case,we get

and

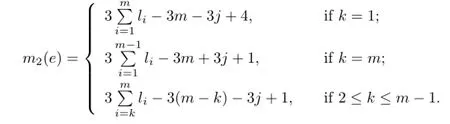
By using the definition of the general third geometric-arithmetic index,we present the general third geometric-arithmetic index of unilateral polyomino chain as follows.

By the definition of linear chain,we have m=1,l1=n,l2=···=lm=0.In terms of Theorem 2.1,we immediately get the following result.

Corollary 2.1Let L4nbe the linear chain with n squares.Then we have

By virtue of the definition of Zig-zag chain,we have m=n−1,and l1=l2=···=lm=2. In view of Theorem 2.1,the following corollary is immediately obtained.

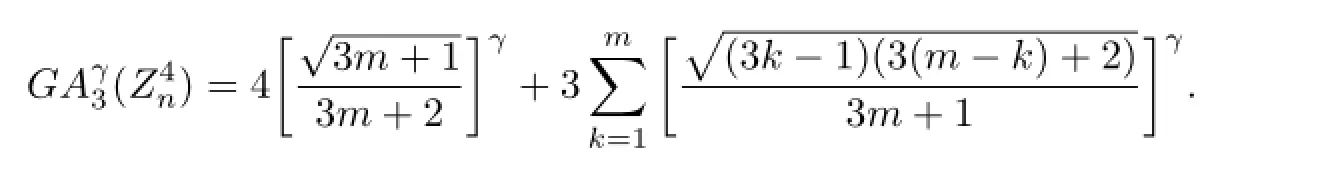
Let γ=1.We can infer the following corollaries for third geometric-arithmetic index.

3　General Third Geometric-arithmetic Index of Hexagonal Chain

Hexagonal chain is one class of hexagonal system which is consisted by hexagonal.In hexagonal chain,each two hexagonals has one common edge or no common vertex.Two hexagonals are adjacented if they have common edge.No three or more hexagonals share one vertex.Each hexagonal has two adjacent hexagonals except hexagonals in terminus, and each hexagonal chain has two hexagonals in terminus.

It is easy to verify that the hexagonal chain with n hexagonals has 4n+2 vertices and 5n+1 edges.Letandbe the linear hexagonal chain and Zig-zag hexagonal chain, respectively.The chemical structure ofandcan refer to Fig.3.1 for more details.

Fig.3.1　The structure ofand

Again,we use the similar trick which was presented in[8]and[19]–[20].We define elementary cut as follows.Choose an edge e of the hexagonal system and draw a straight line through the center of e,orthogonal on e.This line will intersect the perimeter in two end points P1and P2.The straight line segment C whose end points are P1and P2is theelementary cut,intersecting the edge e.A fragment S in hexagonal chain is just maximal linear chain which include the hexagonals in start and end vertices.Let l′(S)be the length of fragment which denotes the number of hexagonals it is contained.Letbe a hexagonal chain with n hexagonals and consist of fragment sequence S1,S2,···,Sm(m≥1).DenoteThen,we verify thatsince each two adjacent fragment have one common hexagonal.For the k-th fragment of hexagonal chain, the cut of this fragment is the cut which intersects withparallel edges of hexagonals in this fragment.A fragment called horizontal fragment if its cut parallels to the horizontal direction,otherwise called inclined fragment.Unilateral hexagonal chain is a special class of hexagonal chain such that the cut for each inclined fragment at the same angle with a horizontal direction.As an example,Fig.3.2 shows a structure of unilateral hexagonal chain.Clearly,linear hexagonal chainis a unilateral hexagonal chain with one fragment, and Zig-zag is a unilateral hexagonal chain with n−1 fragments.

Fig.3.2　I-type cut and II-type cut of unilateral hexagonal chain

Case 1.Edge e is I-type in j-th square of k-th fragment(i.e.,e is edge which is passed by dotted line in Fig.3.2).

For this case,the values of m1(e)and m2(e)are calculated as follows:

Case 2.The edge e is II-type in j-th square of k-th fragment(i.e.,e is edge which is passed by real lines in Fig.3.2).Then,we deduce

Hence,we get the general third geometric-arithmetic index of unilateral hexagonal chain by combining the above cases and the definition.

By the definition of linear chain,we check that m=1,l′1=n,l′2=···=l′m=0.In terms of Theorem 3.1,we shortly deduce the following result.

By using the definition of Zig-zag chain,we verify that m=n−1 andIn view of Theorem 3.1,the following corollary is immediately yielded.

Let γ=1.Then we can obtain the following corollaries for third geometric-arithmetic index.

[1]Yan L,Li Y,Gao W,Li J.PI index for some special graphs.J.Chemical Pharmaceutical Res., 2013,5:260–264.

[2]Yan L,Li Y,Gao W,Li J.On the extremal hyper-wiener index of graphs.J.Chemical Pharmaceutical Res.,2014,6:477–481.

[3]Gao W,Shi L.Wiener index of gear fan graph and gear wheel graph.Asian J.Chemistry, 2014,26:3397–3400.

[4]Gao W,Liang L,Gao Y.Some results on wiener related index and shultz index of molecular graphs.Energy Education Science and Technology:Part A,2014,32:8961–8970.

[5]Xi W F,Gao W.Geometric-arithmetic index and Zagreb indices of certain special molecular graphs.J.Adv.Chem.,2014,10:2254–2261.

[6]Xi W F,Gao W.λ-modified extremal hyper-wiener index of molecular graphs.J.Appl.Comput. Sci.Math.,2014,18:43–46.

[7]Xi W F,Gao W,Li Y.Three indices calculation of certain crown molecular graphs.J.Adv. Math.,2014,9:2696–2304.

[8]Gao W,Wang W F.Second atom-bond connectivity index of special chemical molecular structures.J.Chem.,2014,Article ID 906254,8 pp.,http://dx.doi.org/10.1155/2014/906254.

[9]Gao Y,Gao W,Liang L.Revised Szeged index and revised edge Szeged index of certain special molecular graphs.International J.Appl.Phys.Math.,2014,4:417–425.

[10]Bondy J A,Mutry U S R.Graph Theory.Berlin:Spring,2008.

[11]Vukicevic D,Furtula B.Topological index based on the ratios of geometrical and arithmetical means of end-vertex degrees of edges.J.Math.Chem.,2009,4:1369–1376.

[12]Yuan Y,Zhou B,Trinajstic N.On geometric-arithmetic index.J.Math.Chem.,2010,47: 833–841.

[13]Das K Ch,Gutman I,Furtula B.On the first geometric-arithmetic index of graphs.Discrete Appl.Math.,2011,159:2030–2037.

[14]Madanshekaf A,Moradi M.The first geometric-arithmetic index of some nanostar dendrimers. Iranian J.Math.Chem.,2014,5:1–6.

[15]Fath-Tabar G,Purtula B,Gutman I.A new geometric-arithmetic index.J.Math.Chem.,2010, 47:477–486.

[16]Zhan F Q,Qiao Y F.The second geometric-arithmetic index of the starlike tree with kcomponent.Math.Practice Theory,2014,44:226–229.

[17]Zhou B,Gutman I,Furtula B,Du Z B.On two types of geometric-arithmetic index.Chem. Phys.Lett.,2009,482:153–155.

[18]Eliasi M,Iranmanesh A.On ordinary generalized geometric-arithmetic index.Appl.Math. Lett.,2011,24:582–587.

[19]Gutman I,Klavzar S.An algorithm for the calculation of the Szeged index of benzenoid hydrocarbons.J.Chemical Inform.Comput.Sci.,1995,35:1011–1014.

[20]Wang S,Liu B.A method of calculating the edge-Szeged index of Hexagonal chain.MATCH Commun.Math.Comput.Chem.,2012,68:91–96.

10.13447/j.1674-5647.2016.02.06

date:Dec.23,2014.

The NSF(11401519,11371328,11471293)of China.

E-mail address:gaowei@ynnu.edu.cn(Gao W).