A Concentration Theorem of(R,p)-anders on Hadamard Manifolds

SHAN LIN

(Department of Mathematics,University of Puerto Rico,Rio Piedras Campus, San Juan,Puerto Rico,00923,USA)

Communicated by Gong Gui-hua



A Concentration Theorem of(R,p)-anders on Hadamard Manifolds

SHAN LIN

(Department of Mathematics,University of Puerto Rico,Rio Piedras Campus, San Juan,Puerto Rico,00923,USA)

Communicated by Gong Gui-hua

In this note,we prove a concentration theorem of(R,p)-anders.As a simple corollary,one can prove that(X,p)-anders do not admit coarse embeddings into Hadamard manifolds with bounded sectional curvatures.

expander,(R,p)-ander,concentration theorem,coarse embedding

2010 MR subject classification:46B99,58C99

Document code:A

Article ID:1674-5647(2016)02-0097-08

Coarse Baum-Connes Conjecture is one of the most important conjectures in the noncommutative geometry.It provides an algorithm of calculation of indices of certain differential operators.For example,it implies the zero-in-the-specturm conjecture stating that the Laplacian operator acting on the space of all L2-forms of a uniformly contractible Riemannian manifold has zero in its spectrum(see[1]).The celebrated work of Yu[2]asserts that any metric spaces which can be coarsely embedded into Hilbert space satisfy the Coarse Baum-Connes Conjecture.Later Yu and Kasparov[1]prove that any metric spaces which can be coarsely embedded into a uniformly convex Banach space satisfy the injectivity of Coarse Baum-Connes Conjecture.Recently,Chen et al.[3]prove the maximal Coarse Baum-Connes Conjecture for spaces which admit a fibred coarse embedding into Hilbert space. On the other hand,now it is well-known that expanders do not admit a coarse embedding into Hilbert spaces and there exist expanders which do not admit a coarse embedding into uniformly convex Banach space(see[4]).Gong et al.[5]prove the Coarse Geometric Novikov Conjecture for a large class of expanders,especially the expanders in[4].The Coarse Novikov Conjecture,or the maximal Coarse Novikov Conjecture,is known to be true for more classes of expanders by[6]–[9].Moreover,Oyono-Oyono and Yu[8]also prove isomorphism of the maximal version of the coarse assembly map.These facts make the study of expandersextremely important in the non-commutative geometry.

The non-coarse embeddability of expanders into Hilbert space is triggered by a concentration theorem of expanders.In[10],a concentration theorem of expanders for Banach space whose unit balls are uniformly embeddable into Hilbert space is proved.In[11],the author proves a concentration theorem of expanders for Hadamard manifolds.

Recently,Mimura[12]introduces Banach spectral gap and(X,p)-anders.Here we prove a concentration theorem for(R,p)-anders for Hadamard manifolds.

First,let us recall basics of(X,p)-anders(see[12]).Let G=(V,E)be a finite graph with the vertex set V and the edge set E.Denote the cardinality of V and E by|V|and|E|, respectively.The degree of a vertex v is the number of edges incident to v.The maximum degree of G,denoted by∆(G),is the maximum degree of its vertices.We equip G with the path metric and regard as a metric space.

Definition 1[12]Let(X,p)be a pair of a Banach space X and an exponent p＞0.

(I)The Banach spectral gap is defined as follows:the(X,p)-spectral gap of G,written as λ1(G;X,p),is

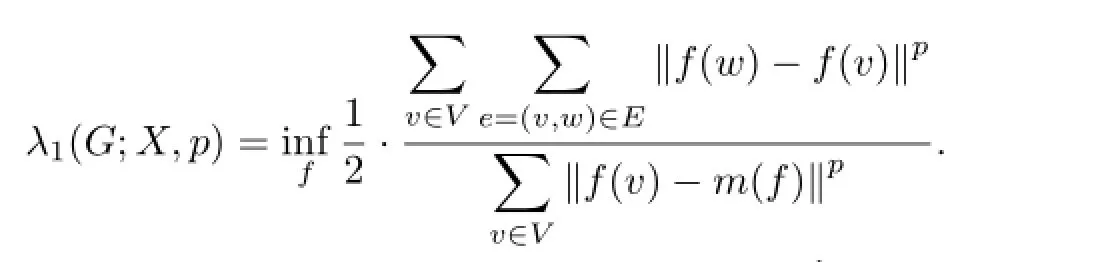
(II)A sequence of finite connected graphs{Gn}is called(X,p)-anders if the following three conditions are satisfied:

A graph is called regular if every vertex has the same degree.A graph is called simple if there is no edge connecting a vertex to itself.From now on,we focus on regular and simple graphs.

Since R can be isometrically embedded into any non-trivial Banach space X,we have

Hence(X,p)-anders are(R,p)-anders.

In the following calculations,we repeatedly use Jensen’s inequality

for convex function ϕ.Norm functions and xpwith p≥1 are convex functions.

Proposition 1(Concentration Property for Euclidean spaces)Let G=(V,E)be a regular, simple graph with∆(G)=k.For any f:V→Rr,

Proof.If f is constant,then the proposition is trivial.Now assume that f is not constant. Take the standard orthonormal basisof Rrand write f in this basis.Let fidenote the i-th coordinate of f,i.e.,fi=〈f,ei〉.Then fi:V→R.Without loss of generality,we assume that all fi’s are not constant.Applying the definition of λ1(G;R,p),

Hence

This completes the proof.

This proposition implies that regular,simple(R,p)-anders cannot admit coarse embeddings into Euclidean space for all p≥2.

Let M be a Hadamard manifold,i.e.,M is a simply-connected complete Riemannian manifold with nonpositive sectional curvatures.For any m ∈M,the exponential map expm:TmM → M is a diffeomorphism and the inverse of exponential map logm:M →TmM is a Lipschitz map with Lipschitz constant 1.

For any m∈M and r＞0,define

By comparison theorem,we have the following lemma.

Lemma 1Let M be a Hadamard manifold with bounded sectional curvatures.Then there exists a ω(r)such that for any m∈M,ωm(r)＜ω(r)for all r＞0 andrli→m0ω(r)=0.

Any n points in Hadamard manifold can have a mean in the following sense.

To prove the main theorem,the following simple inequalities are useful.

Proof.The proof consists of two simple computations.That is,

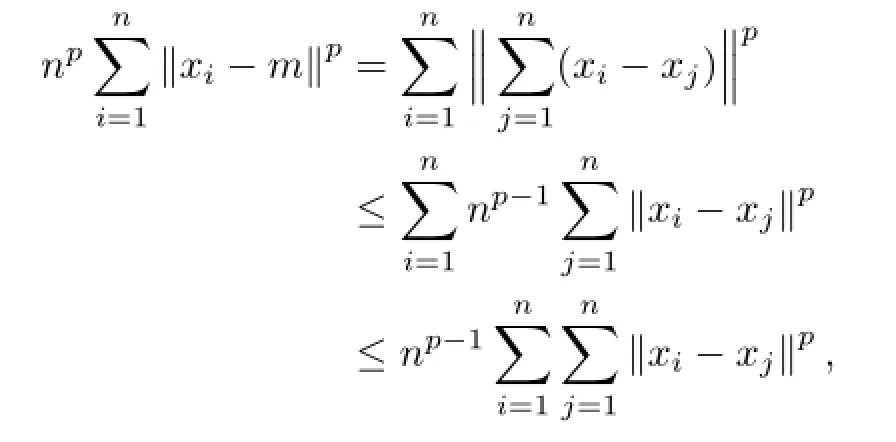
and

Hence

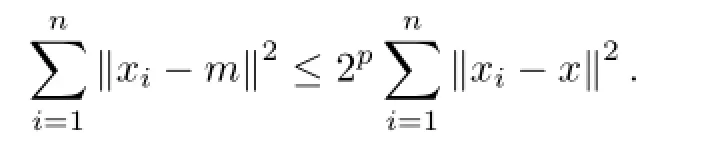
Lemma 4Let G=(V,E)be a regular and simple graph with∆(G)=k,λ=λ1(G;R,p).

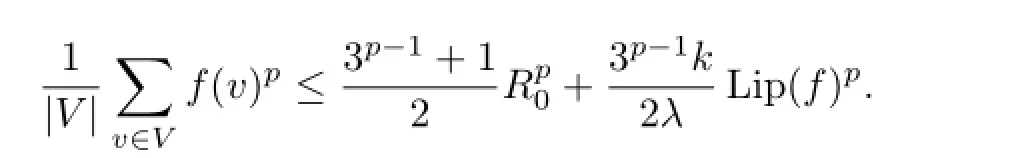
Then

where

by Proposition 1.This completes the proof.

These proofs do not work for 0＜p＜1 since the function xpis not convex.

Let G=(V,E)be a regular simple graphs with∆(G)=k and λ=λ1(G;R,p),and M be a Hadamard manifold.For f:V→M,define

Then

Define αv:[0,1]→M such that the image of αvis the geodesic connecting m and f(v)with αv(0)=m,αv(1)=f(v)and d(αv(t),m)=td(m,f(v)).Since the distance function of M is convex,we have d(αv(t),αw(t))≤td(f(v),f(w))for any v,w∈V.Hence Lip＜1.

Now let us prove the main theorem.

Theorem 1Let M be an r-dimensional Hadamard manifold with bounded sectional curvatures.And let G=(V,E)be a regular simple(R,p)-anders with∆(G)=k,λ= λ1(G;R,p),p≥2.Then there exists an R＞0 such that for any f:V→M,

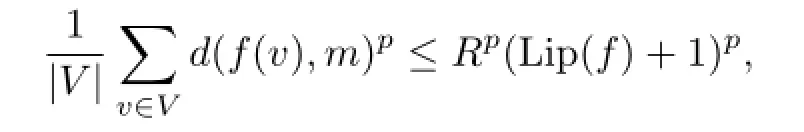
where m is a point such that∑

Proof.We prove the theorem by contradiction.Choose an R＞0 large enough such that

for some integer N to be determined,where ω is defined in Lemma 1.Suppose that there exists a map f:V→M such that

Without loss of generality,we assume that

with Lip(f)＜1.Choose an R0＞0 such that there exists a v0∈V such that

We assume that R0attains its infimum with v0under this condition.Define∥f∥:V→R+by∥f∥(v)=∥logm(f(v))−logm(f(v0))∥for all v∈V.Then

So,by Lemmas 3 and 4,we have

Hence,

Define

Then

So by Proposition 1,we have

where

1we haveChoose v∈A.Note that for11

v∈A1,we have∥g(v)−g(v1)∥≤8δ and hence

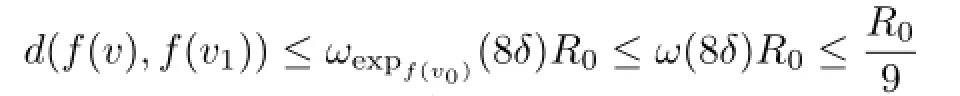
by the assumption on R and Lemma 4.It follows that

Choose a sufficiently large N(N depends on p)such that

Therefore,we get the cardinality

i.e.,

which contradicts the minimality of R0.This completes the proof.

Let X and Y be two metric spaces.ϕ:X→Y is said to be a coarse embedding if there exist two non-decreasing maps ρ1,ρ2:[0,∞)→[0,∞)such that for all x,y∈X,

and

A sequence of metric space{Xn}is said to be equi-coarsely embeddable into a metric space Y if there exist ϕn:Xn→Y for all n∈N and two non-decreasing maps ρ1,ρ2: [0,∞)→[0,∞)such that for all xn,yn∈Xn

and

The sequence{ϕn}is called an equi-coarse embedding of{Xn}into Y.

As a simple application of Theorem 1,we have the following corollary.

Corollary 1An(X,p)-ander with p≥2 does not admit an equi-coarse embedding into finite dimensional Hadamard manifolds with bounded sectional curvature.

See[14]–[15]for the relation with the Coarse Geometric Novikov Conjecture in this case.

[1]Kasparov G,Yu G.The coarse geometric Novikov conjecture and uniform convexity.Adv. Math.,2006,206(1):1–56.

[2]Yu G.The coarse Baum-Connes conjecture for spaces which admit a uniform embedding into Hilbert space.Invent.Math.,2000,139(1):201–240.

[3]Chen X,Wang Q,Yu G.The maximal coarse Baum-Connes conjecture for spaces which admit a fibred coarse embedding into Hilbert space.Adv.Math.,2013,249:88–130.

[4]Lafforgue V.Un renforcement de la propri´et´e(T).Duke Math.J.,2008,143(3):559–602.

[5]Gong G,Wang Q,Yu G.Geometrization of the strong Novikov conjecture for residually finite groups.J.Reine Angew.Math.,2008,621:159–189.

[6]Chen X,Tessera R,Wang X,Yu G.Metric sparsification and operator norm localization.Adv. Math.,2008,218(5):1496–1511.

[7]Guentner E,Tessera R,Yu G.Operator norm localization for linear groups and its applications to K-theory.Adv.Math.,2010,226(4):3495–3510.

[8]Oyono-Oyono H,Yu G.K-theory for the maximal Roe algebra of certain expanders.J.Funct. Anal.,2009,257(10):3239–3292.

[9]Willett R,Yu G.Higher index theory for certain expanders and Gromov monster groups I. Adv.Math.,2012,229:1380–1416.

[10]Ozawa N.A note on non-amenability of B(ℓp)for p=1,2.Internat.J.Math.,2004,15: 557–565.

[11]Shan L.A concentration theorem of expanders on Hadamard manifolds.J.Funct.Anal.,2012, 263(1):109–114.

[12]Mimura M.Sphere equivalence,Banach expanders,and extrapolation.preprint.

[13]Dranishnikov A N.Dimension theory local and global properties.preprint.

[14]Shan L.An equivariant higher index theory and nonpositively curved manifolds.J.Funct. Anal.,2008,255(6):1480–1496.

[15]Shan L,Wang Q.The coarse geometric Novikov conjecture for subspaces of non-positively curved manifolds.J.Funct.Anal.,2007,248(2):448–471.

10.13447/j.1674-5647.2016.02.01

date:Sept.2,2014.

E-mail address:lin.shan@upr.edu(Shan L).