On the Adomian Decomposition Method for Solving PDEs

ZHU SONG-pINGAND LEE JONU

(1.School of Mathematics,Jilin University,Changchun,130012)

(2.School of Mathematics and Applied Statistics,University of Wollongong, Wollongong,NSW 2522,Australia)

Communicated by Wang De-hui



On the Adomian Decomposition Method for Solving PDEs

ZHU SONG-pING1,2AND LEE JONU2

(1.School of Mathematics,Jilin University,Changchun,130012)

(2.School of Mathematics and Applied Statistics,University of Wollongong, Wollongong,NSW 2522,Australia)

Communicated by Wang De-hui

In this paper,we explore some issues related to adopting the Adomian decomposition method(ADM)to solve partial differential equations(PDEs),particularly linear diffusion equations.Through a proposition,we show that extending the ADM from ODEs to PDEs poses some strong requirements on the initial and boundary conditions,which quite often are violated for problems encountered in engineering,physics and applied mathematics.We then propose a modified approach, based on combining the ADM with the Fourier series decomposition,to provide solutions for those problems when these conditions are not met.In passing,we shall also present an argument that would address a long-term standing“pitfall”of the original ADM and make this powerful approach much more rigorous in its setup.Numerical examples are provided to show that our modified approach can be used to solve any linear diffusion equation(homogeneous or non-homogeneous),with reasonable smoothness of the initial and boundary data.

Adomian decomposition method,non-smooth initial condition,linear PDEs

2010 MR subject classification:49M27,35Q79

Document code:A

Article ID:1674-5647(2016)02-0151-16

1　Introduction

The Adomian decomposition method(ADM),as a powerful numerical approach initially proposed by Adomian[1]–[4]in 1980s,has been successfully applied to solve various ordinary differential equations(ODEs).And yet,its extension to solving partial differential equations(PDEs)are far less investigated and many issues remain to be resolved before the powerfulness of this method can be further stretched into the territory of PDEs.In this paper, we discuss the applicability of the ADM to the simplest PDE,the linear parabolic PDEs with inhomogeneous terms and demonstrate,through a proposition,that one needs to be careful in extending ADM to PDEs as there is a very strong requirement of the smoothness of the boundary and initial data.On the other hand,quite a lot of problems frequently encountered in engineering and applied mathematics do not have sufficient smoothness in terms of boundary and/or initial conditions and a direct imposition of the ADM,as some authors did,would lead to a wrong solution.For example,the solutions of Example 4 in[5] and Examples 1 and 2 in[6]satisfy the given PDEs and initial conditions but they do not satisfy the given boundary conditions.To rectify the problem,we have proposed a modified approach,which combines the ADM and Fourier expansion and leads to a much robust approach to solve linear PDEs.

Using ADM to solved ODEs has been extensively documented in the literature.The method was initially proposed by Adomian[1]–[4]and then later extended to solve various ODEs,ranging from single ones(see[7])to systems of ODEs(see[8]),from ODEs with variable coefficients(see[9])to highly nonlinear ones(see[10]–[11]),and from deterministic ODEs(see[12])to stochastic equations(see[13]–[14])or even nonlinear ODEs that exhibit singular behavior at the origin(see[9]).One of the main advantages of the ADM is that the convergence of the Adomian series solution has been proven in the context of its applications in solving ODEs(see[15]–[20]).

On the other hand,the ADM has also been applied to solve various PDEs.For example, PDEs with Dirichlet boundary conditions were studied in[21]–[23],and those with Neumann boundary conditions were studied in[12].In terms of PDEs with very strong application backgrounds,Tatari et al.[24]applied the ADM to solve the Fokker-Planck equation,which is frequently used in mathematical finance,while Inc and Cherruault[25]applied it to the KdV (Korteweg-de Vries)equation,which appears frequently in mathematical physics and Arafa and Rida[26]applied it to solve the nonlinear Schr¨odinger equation,which often governs soliton propagation in optical fibers.In most of the papers showing ADM being applied to solve PDEs with both initial and boundary conditions(e.g.,[5]–[6],[27]–[28]),all given boundary and initial conditions are composed of smooth functions.For example,using smooth boundary conditions,Wazwaz[29]and Aly et al.[12]suggested some strategies for finding exact solutions of nonlinear PDEs.There are also researchers who have applied ADM to coupled nonlinear PDEs(see[30]–[31])with smooth initial conditions.Unfortunately, until now,there has been no attempt to get approximate or analytic solutions of PDEs, using the ADM,with non-smooth boundary or initial conditions.

Despite some limited attempts to extend the ADM to solve PDEs,the application of ADM to solve PDEs are relatively rare in comparison with their ODE counterparts and one of the main reasons is the lack of theoretical studies in terms of guaranteeing the solution to satisfy all the initial and boundary conditions.This is because when ADM is extended from ODEs to PDEs,its characteristic of repeatedly integrating in one direction remains,whichresults in the solution of a PDE be written in a form that deviates quite away from a solution that would satisfy the boundary conditions in the direction in which the integration is not performed.Also,non-smooth boundary or initial conditions are frequently encountered in applied mathematics and physics.For instance,a typical heat transfer problem is presented in Example 4.1 of this paper.We shall demonstrate,through a proposition,the reason why the conventional ADM does not work for the PDE system(4.1)with the initial profile being of the form(4.2),as well as some appropriate requirement on the smoothness of the given boundary and initial information,under which all the boundary conditions are satisfied.

In the remaining paper,we shall first prove a proposition that forms the theoretic base for the ADM to be extended to solve linear homogeneous diffusion equations.We shall show through this proposition that the extension of the ADM to this simplest PDE system poses some very strong conditions on the smoothness of the boundary and initial condition before a solution can be worked through the ADM.These conditions are so strong that some frequently encountered problems in applied mathematics and engineering could not be tackled by this power method anymore.Therefore,we propose a modified ADM,which will can be used to deal with those cases for which a direct application of the ADM will fail.Of course,as shall be shown later,there are some degrees of resemblance between out modified ADM and eigenfunction expansion in solving linear PDEs.But,we believe that our modified ADM will shed some lights in using this powerful method to solve nonlinear PDEs eventually,because the application of ADM in solving nonlinear ODEs has been well documented in the literature as mentioned earlier.

2　Application of ADM to Solve PDEs

The extension of ADM to solve PDEs may not be as trivial as one would initially thought, simply because the method is based on recursively integrating the PDE with respect to a particular direction to construct a solution in series form.Naturally,one would raise questions such as

•Under what conditions,the method would lead to a convergent solution,for a given set of boundary and initial data;

•Unlike ODEs,there are at least two independent variables for PDEs.Therefore,the solution obtained after integrating with respect to a particular variable and thus has satisfied all the boundary/initial conditions in that direction also satisfies other boundary/initial conditions,which do not explicitly appear in the solution process when one extend the ADM from solving ODEs to PDEs;

•Above all,we would like to know the condition under which the solutions obtained from integrating with respect to different independent variables are essentially the same solution.

Let us first explore the solution of the following PDE system using the classic ADM and establish some sufficient conditions for the ADM to render consistent solutions no matter which direction one chooses to integrate with respect to.

Consider

where a is a constant,p,q and f are given functions.

Proposition 2.1If the given functions p,q and f in(2.1)satisfy the following conditions:

(iii)f,p,q∈C∝,f is analytic(see[32])at 0,1 and p and q are analytic at 0, then

(1)the solution of the PDE in(2.1)can be written as

if one integrates(2.1)in the t-direction through the ADM and

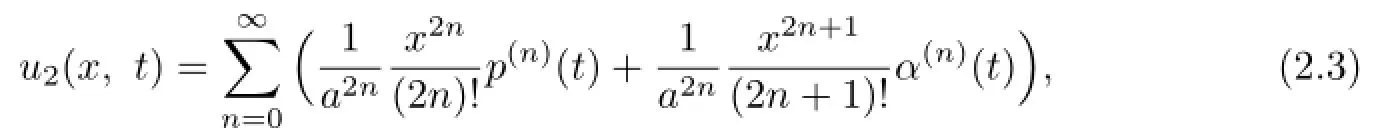
if one integrates(2.1)in the x-direction,where

(2)two forms are equivalent,and

(3)all BCs and the IC are satisfied.

In the above,f(n)denotes the nth derivative of f with respect to x.

Proof.(1)(i),(ii)and(iii)are equivalent to(i′),(ii)and(iii).

First,we prove that“If f(x)/≡0,then p(t)/≡0 or q(t)/≡0”.

Suppose f(x)/≡0.Let us assume for the sake of contradiction that p(t)≡0 and q(t)≡0. From Condition(ii),i.e.,for all n=0,1,2,···,we have

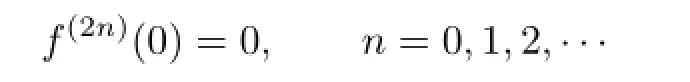
Now,we need to prove that the odd derivatives of f at x=0 are zero too.From Condition(iii),we have

Therefore,

and we can calculate

From Conditions(ii)and(iii),(2.5)leads to

upon utilizing the above proven fact thatfor all n=0,1,2,···

Therefore,q(t)≡0 implies thatfor any m and n,because(2.6)holds for any t.Or equivalently,we conclude that

Now,since f is also assumed to analytic at 0(Condition(iii)),for all n=0,1,2,···leads to the conclusion that f(x)≡0.Therefore a contradiction has been reached,which implies that p(t)/≡0 or q(t)/≡0.

On the other hand,we need to show that“If p(t)/≡0 or q(t)/≡0,then f(x)/≡0”.

Now we start with p(t)/≡0 or q(t)/≡0.If we also assume that f(x)≡0,then,from Condition(ii),we have

Thus,from Condition(iii),we conclude that p(t)≡0 and q(t)≡0,which are contradictory to the given conditions that p(t)/≡0 or q(t)/≡0.Therefore,f(x)/≡0.

(2)u1(x,t)given in(2.2)and u2(x,t)in(2.3)are solutions of(2.1).

The satisfaction of the PDE in(2.1)by both u1(x,t)and u2(x,t)can be easily verified by taking the partial derivatives against t once and x twice.

On the other hand,we need verify that u1(x,t)and u2(x,t)satisfy all BCs and the IC in PDE system(2.1).The proof for the satisfaction of the BCs and the IC by u1(x,t)is straightforward,as

upon a direct substitution of the boundary and initial values into u1(x,t),together with Conditions(ii)and(iii).

The verification of the BC by u2(x,t)at x=0 is easy:

However,the proof of the satisfaction of the BC at the right end x=1 is not so straightforward and we need to use mathematical induction to show

With k=0,we can easily verify,from(2.3),(2.4)and(2.5),that

Hence we conclude that

which leads to

Having shown the satisfaction of the BCs,let us now show the satisfaction of the IC of u2(x,t).From(2.3),we have

We now can conclude that the classic ADM can indeed be extended to solve(2.1),yielding the solution of u1(x,t),if Conditions(i),(ii)and(iii)are met,or u2(x,t),if Conditions(i′), (ii)and(iii)are met.If all these conditions are met,then one can adopt either u1(x,t)or u2(x,t)as the solution.One naturally wonders if these two are the same in this case,which is discussed next.

(3)u1(x,t)=u2(x,t),if(i),(i′),(ii)and(iii)all hold at the same time.

In(2),we have shown that u1(x,t)and u2(x,t)are two different forms of solution, satisfying(2.1).But,from the uniqueness of(2.1)(cf.[33]),we should be able to show that these two“seemingly-different”solutions are actually the same.This is indeed so as we can prove as below1.

The proof of Proposition 2.1 is completed.

It is quite interesting to have observed that only the even order of derivatives f(2n)(x) are used in Proposition 2.1;one may wonder why the odd derivatives are not used at all.In fact,the information contained in the odd derivatives of f(2n+1)(x)is used to compute the first order derivative of u with respect to x,as shown in the following Corollary.

1In the proof,we need to use the nth order derivative of the Taylor expansion of p(t)and α(t):

Corollary 2.1

Before leaving this section,it should be remarked that it is extremely important to pay attention to the conditions in Proposition 2.1,if the ADM is to be used to solve PDEs.In the ADM literature,there were cases where authors just bluntly apply the ADM to solve a PDE system,without paying any attention to the conditions in Proposition 2.1.Naturally, when these conditions are not satisfied,the ADM has led to totally wrong results.[5]–[6] are examples in this category,among others.

3　A Modified ADM

In light of the strong conditions required by the classic ADM,which are quite often not met in many problems encountered in engineering,physics and applied mathematics,we propose a modified ADM to solve linear PDEs with much more relaxed requirements on the initial and boundary conditions.

Our modified ADM is introduced for the linear diffusion equation with non-homogeneous source term but with homogeneous boundary conditions

where g and r are given functions.The extension of this approach to a more general PDE system with inhomogeneous boundary conditions are discussed later.

Taking advantage of the homogeneous boundary conditions in(3.1),the modified ADM begins with expanding g(x,t)and r(x)in Fourier sine series of functions as

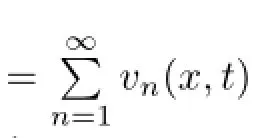
So,now we can solve for each individual component vn(x,t)by solving the PDE system

This is of course a system that perfectly satisfies all the conditions required by the classic ADM as stated in Proposition 2.1.

PDE system(3.5)can be further split intowithandsatisfying the following two PDE systems,respectively,

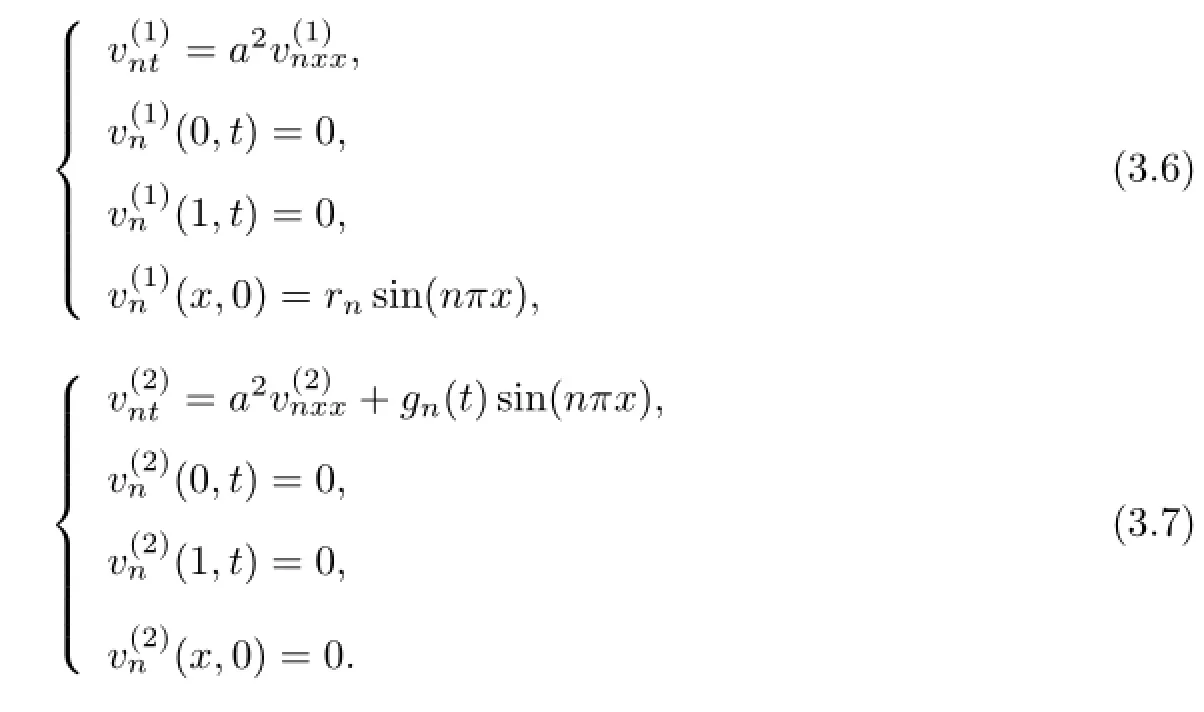
Now we can apply the ADM to(3.6)first.Let us consider the operator Ltand Lxxdefined by

Applying the inverse operatoron both sides of(3.8)yields

Let

Then we have

Thus,the solution of the first PDE system(3.6)becomes

Now,for the second PDE system(3.7),the solution for the inhomogeneous governing PDE is of the form

Upon substituting this into the governing equation in(3.7),we obtain an ODE system

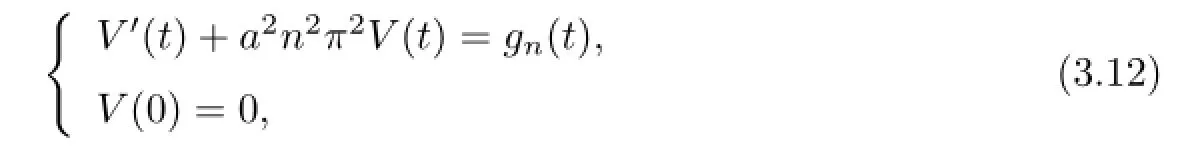
the solution of which can be easily obtained as

Combing the two solutions(3.11)and(3.14),we obtain the desired solution for(3.5)as

and hence we finally obtain the solution of the PDE system(3.1)as

where gn(t)and rnare given in(3.2)and(3.3),respectively.

Although the above approach is limited to the linear inhomogeneous diffusion problems with homogeneous boundary conditions,extending its coverage to a more general case without the restrictions to the homogeneity of the boundary conditions can be easily completedwith construction of a functional transform.Consider the most general initial boundary value problem for the heat equation as follows

where G,P,Q and F are given functions and P and Q are differentiable.If we take

where

then(3.17)is equivalent to(3.1)provided

and

So the solution w(x,t)can be found by using formula(3.16)as

where,in this case,

Before finishing this section,we should remark that one can easily verify,as expected, the formula(2.2)for the solution of(2.1)presented in Proposition 2.1 is a special case of (3.18)by letting G(x,t)≡0,while(3.18)degenerates to(3.16)when P(t)≡0 and Q(t)≡0.

0

4　Examples

In this section,we present a couple of examples,showing the application of ADM to linear diffusion problems.

Example 4.1Consider the following homogeneous heat equation system with non-smooth initial conditionwhere h(x)is of the following form

If the classic ADM is directly applied to solve this problem,with an integration along the t direction,it will lead to a failure,as a result of the initial condition h(x)does not have enough smoothness to satisfy the condition(iii)in Proposition 2.1.On the other hand,if one applies the modified ADM as proposed in Section 3,one can then use the formulae (3.16),(3.2)and(3.3)with a=1,g(x,t)=0,to obtain

with which we can easily obtain the solution in an infinite series form as

Of course,one can easily verify that the obtained solution is identical to the one obtained with the method of separation of variables for this problem.This is not surprising at all because the essence of our modified ADM is to decompose a case not debatable by the classic ADM into a sum of infinite many cases,each of which satisfies the conditions in Proposition 2.1.

Example 4.2Now,we consider a linear inhomogeneous diffusion problem with source term described by the following PDE system:

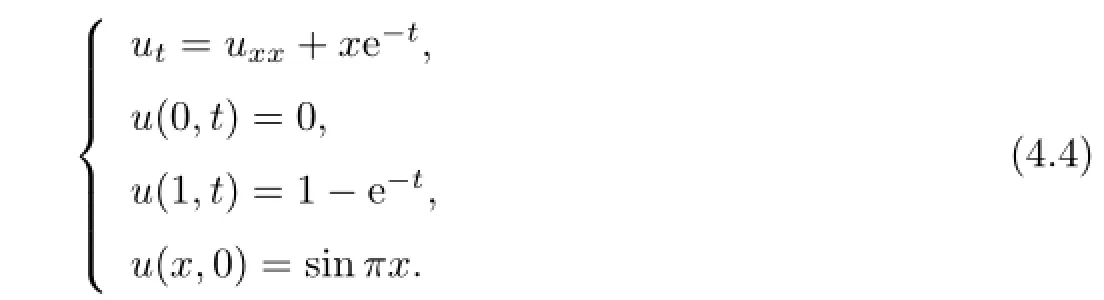
Using the formulae(3.18)–(3.20)with v(x,t)=u(x,t)−H(x,t),a=1,H(x,t)=x(1−e−t), g(x,t)=0,r(x)=sinπx,and

we can easily recover the exact solution

without the need of involving an infinite series at all.Of course,the main reason is that there is only one Fourier component involved in the initial condition.

Example 4.3Consider the following inhomogeneous heat equation system:

Through a similar way as that shown in Example 4.2,we know that v(x,t)=u(x,t)−H(x,t), a=2,So we obtain that

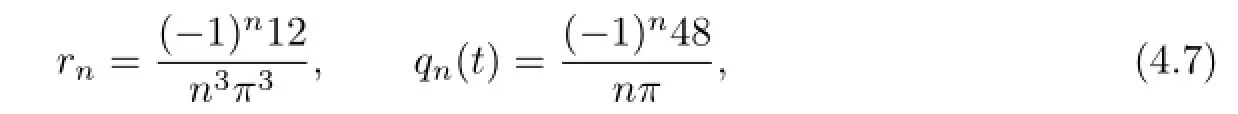
with which the solution of(4.6)can be easily constructed as

Of course,this solution is identical to the exact solution of the problem

if one realizes that the infinite series contained in(4.8)is nothing but x3−x.

5　Conclusion

Through the proposition presented in this paper,we have found that extending the classic ADM method from solving ODEs to solving PDEs requires some very strong conditions on the smoothness of the initial and boundary data.These conditions may not be met in most of the problems encountered in applied mathematics and engineering.We have then proposed a modified ADM based on the Fourier series expansion on the initial and boundary conditions first and applied this modified ADM to solve the most general linear non-homogeneous diffusion equation with the source term being independent of the unknown function.Our numerical examples show that the proposed modified ADM can indeed produce excellent results after we have verified this approach through comparing the results obtained from this modified ADM with those obtained from the exact solution.

Appendix

In this Appendix,we show the solutions(2.2)and(2.3)in Proposition 2.1 are obtained by adopting the ADM to integrate along the t-direction and x-direction,respectively.

Case IIntegrate along the t-direction

The ADM procedure begins with rewriting the PDE in the form

one can then apply this inverse operator on both sides of(A1)and obtain

upon imposingthe initial condition u(x,0)=f(x).Next,the solution u(x,t)is written in the form of an infinite series,with the nth component being denoted as un(x,t)in the ADM solution approach

and u0(x,t)is usually assigned with the initial condition u(x,0).Substituting(A4)into (A3)yields

which then leads to a recursive solution for each component un(x,t)

Then,as a result of the split of operatorsand Lxxin(A6),the recursive procedure can actually be carried out,yielding an explicit solution of the component un(x,t)in terms of the 2n-th order of the derivative of the initial data f(x)

Clearly,summing up all these components leads to(2.2),which is the first solution form in Proposition 2.1.

Case IIIntegrate along the x-direction

On the other hand,one can also rewrite the PDE in(2.1)as follows:

If one assumes that the inverse operatorof Lxxexists and it can be taken as the double integral

one can then apply this inverse operator on both sides of(A8),upon using the boundary condition u(0,t)=p(t),to produce

where α(t)is an unknown function to be determined.

Substituting(A4)into(A10)yields

which then leads to a recursive solution for each component un(x,t)

Then,as a result of the split of operatorsand Ltin(A12),the recursive procedure can be actually carried out,yielding an explicit solution of the component un(x,t)in terms of the n-th order of the derivatives of p(t)and α(t)

Summing up all these components leads to(2.3),which is the second solution form in Proposition 2.1.

Finally,using the initial condition in(2.1),we can easily obtain the α(t)as stated in (2.4).

[1]Adomian G.Stochastic Systems.New York:Academic,1983.

[2]Adomian G.Nonlinear Stochastic Operator Equations.Orlando:Academic,1986.

[3]Adomian G.Nonlinear Stochastic Systems Theory and Applications to Physics.Dorderecht: Kluwer Academic,1989.

[4]Adomian G.Solving Frontier Problems of Physics:The Decomposition Method.Dorderecht: Kluwer Academic,1994.

[5]Wazwaz A M.Equality of partial solutions in the decomposition method for partial differential equations.Internat.J.Comput.Math.,1997,65(3–4):293–308.

[6]Gorguis A,Benny Chan W K.Heat equation and its comparative solutions.Comput.Math. Appl.,2008,55(12):2973–2980.

[7]Duan J S,Rach R.A new modification of the Adomian decomposition method for solving boundary value problems for higher order nonlinear differential equations.Appl.Math.Comput.,2011,218(8):4090–4118.

[8]Duan J S.Convenient analytic recurrence algorithms for the adomian polynomials.Appl.Math. Comput.,2011,217(13):6337–6348.

[9]Wazwaz A-M,Rach R,Duan J-S.Adomian decomposition method for solving the Volterra integral form of the Lane-Emden equations with initial values and boundary conditions.Appl. Math.Comput.,2013,219(10):5004–5019.

[10]Rach R,Wazwaz A M,Duan J S.A reliable modification of the Adomian decomposition method for higher-order nonlinear differential equations.Kybernetes,2013,42(2),282–308.

[11]El-Kalla I L.A new result on the analytic summation of Adomian series for linear and nonlinear differential equations.Internat.J.Appl.Math.Comput.,2010,2(2):1–10.

[12]Aly E H,Ebaid A,Rach R.Advances in the Adomian decomposition method for solving twopoint nonlinear boundary value problems with Neumann boundary conditions.Comput.Math. Appl.,2012,63(6):1056–1065.

[13]Adomian G,Rach R.Inversion of nonlinear stochastic operators.J.Math.Anal.Appl.,1983, 91(1):39–46.

[14]Adomian G,Rach R.Nonlinear stochastic differential delay equations.J.Math.Anal.Appl., 1983,91(1):94–101.

[15]Rach R.A new definition of the Adomian polynomials.Kybernetes,2008,37(7):910–955.

[16]Cherruault Y.Convergence of Adomian’s method.Kybernetes,1989,18(2):31–38.

[17]R`epaci A.Nonlinear dynamical systems:On the accuracy of adomian’s decomposition method. Appl.Math.Lett.,1990,3(4):35–39.

[18]Abbaoui K,Cherruault Y.Convergence of Adomian’s method applied to differential equations. Comput.Math.Appl.,1994,28(5),103–109.

[19]Gabet L.The theoretical foundation of the Adomian method.Comput.Math.Appl.,1994, 27(12):41–52.

[20]Abdelrazec A,Pelinovsky D.Convergence of the Adomian decomposition method for initialvalue problems.Numer.Methods Partial Differential Equations,2011,27(4):749–766.

[21]Adomian G.Solutions of nonlinear P.D.E.Appl.Math.Lett.,1998,11(3):121–123.

[22]Garcia-Olivares A.Analytic solution of partial differential equations with Adomian’s decomposition.Kybernetes,2003,32(3):354–368.

[23]Zhang B,Lu J.Exact solutions of homogeneous partial differential equation by a new adomian decomposition method.Procedia Environmental Sciences,2011,11(Part A),440–446.

[24]Tatari M,Dehghan M,Razzaghi M.Application of the adomian decomposition method for the Fokker-Planck equation.Math.Comput.Modelling,2007,45(5-6):639–650.

[25]Inc M,Cherruault Y.A reliable approach to the Korteweg-de Vries equation:An application of the decomposition method.Kybernetes,2005,34(7/8):951–959.

[26]Arafa A A M,Rida S Z.Numerical solutions for some generalized coupled nonlinear evolution equations.Math.Comput.Modelling,2012,56(11-12):268–277.

[27]Luo X G.A two-step adomian decomposition method.Appl.Math.Comput.,2005,170(1): 570–583.

[28]Mustafa I.Decomposition method for solving parabolic equations in finite domains.J.Zhejiang Univ.Science,2005,6A(10):1058–1064.

[29]Wazwaz A M.A note on using Adomian decomposition method for solving boundary value problems.Found.Phys.Lett.,2000,13(5):493–498.

[30]Ray S S.An application of the modified decomposition method for the solution of the coupled Klein-Gordon-Schr¨odinger equation.Comm.Nonlinear Sci.Numer.Simulation,2008,13(7): 1311–1317.

[31]Alharbi A,Fahmy E S.ADM-Pad´e solutions for generalized Burgers and Burgers-Huxley systems with two coupled equations.J.Comput.Appl.Math.,2010,233(8):2071–2080.

[32]Thomson B S,Bruckner A M,Bruckner J B.Elementary Real Analysis(2nd Edition).ClassicalRealAnalysis.com.,2008.

[33]Kevorkian J.Partial Differential Equations:Analytical Solution Techniques.California:Pacific Grove,1990.

10.13447/j.1674-5647.2016.02.08

date:Sept.5,2014.

E-mail address:spz@uow.edu.au(Zhu S P).