A Fixed Point Approach to the Fuzzy Stability of a Mixed Type Functional Equation

CHENG LI-HUAAND ZHANG JUN-MIN

(1.School of Science,Xi’an Polytechnic University,Xi’an,710048)

(2.School of Science,Xi’an University of Architecture and Technology,Xi’an,710055)

Communicated by Ji You-qing



A Fixed Point Approach to the Fuzzy Stability of a Mixed Type Functional Equation

CHENG LI-HUA1AND ZHANG JUN-MIN2

(1.School of Science,Xi’an Polytechnic University,Xi’an,710048)

(2.School of Science,Xi’an University of Architecture and Technology,Xi’an,710055)

Communicated by Ji You-qing

Through the paper,a general solution of a mixed type functional equation in fuzzy Banach space is obtained and by using the fixed point method a generalized Hyers-Ulam-Rassias stability of the mixed type functional equation in fuzzy Banach space is proved.

mixed functional equation,Hyers-Ulam stability,Fuzzy Banach space, fixed point

2010 MR subject classification:46S40,47S40,47H10,39B52

Document code:A

Article ID:1674-5647(2016)02-0122-09

1　Introduction

The stability problem of functional equation originated from a question of Ulam[1]in 1940, concerning the stability of a group hmomorphisms.Heyers[2]gave a first affirmative partial answers to the question of Ulam for Banach spaces.Heyers theorem was generalized by Aoki[3]for additive mapping and by Rassias[4]for linear mappings by considering an unbounded Cauchy difference.A generalization of the Rassias theorem was obtained by Gˇavruta[5]by replacing the unbounded Cauchy difference by a general control function in the spirit of Rassias’approach.

The functional equation is said to be a quadratic function.

The following cubic functional equation was introduced by Rassias[6]:

The function f(x)=x3satisfies(1.2),which is called cubic functional equation.And he established the general solution and the generalized Hyers-Ulam-Rassias stability for(1.2).

Later,Gordji et al.[7]studied solution and stability of mixed type additive-quadraticcubic functional equation:

Choonkil[8]gave a fixed point approach to the fuzzy stability of an additive-quadraticcubic functional equation:

By using the fixed point methods,the stability problems of several functional equations have been extensively investigated by a number of authors,more reference can be seen in [9]–[10].

In this sequel,we adopt the usual terminology,notations and conventions of the theory in[10].

Definition 1.1[10]Let X be a real linear space.A function N:X×R→[0,1]is said to be fuzzy norm on X,if for all x,y∈X and all a,b∈R,

(1)N(x,a)=0 for a≤0;

(2)x=0 if and only if N(x,a)=1 for a＞0;

(4)N(x+y,a+b)≥min{N(x,a),N(x,b)};

(6)for x/=0,is continuous on R.

The pair(X,N)is called a fuzzy normed linear space,where X is a linear space and N is a fuzzy norm on X.In the following,we suppose that N(x,a)is left continuous for every x.A sequence{xn}in X is said to be convergent if there exists an x∈X such thatIn that case,x is called N-convergent,and denoted by.A sequence{xn}in fuzzy normed space(X,N)is called Cauchy sequence if for each ε＞0 and δ＞0,there exists an n0∈N such that

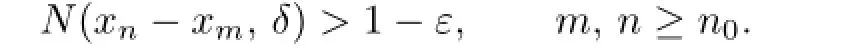
If each Cauchy sequence is convergent,then the fuzzy norm is said to be complete and the fuzzy normed space is called a fuzzy Banach space.

Let X be a set.A function d:X×X→[0,+∞]is called a generalized metric on X if d satisfies:

(1)d(x,y)=0 if and only if x=y;

(2)d(x,y)=d(y,x)for all x,y∈X;

(3)d(x,z)≤d(x,y)+d(y,z).

Theorem 1.1Let(Ω,d)be a complete generalized metric space,and T:Ω→Ω be a strictly contractive mapping with Lipschitz constant L＜1.Then for each given element x∈Ω,either

for all nonnegative integers n,or there exists a positive integer n0∈N,such that

(1)for all n＞n0,d(Tnx,Tn+1x)＜∞;

(2)for all n＞n0,the sequence{Tnx}converges to a fixed point y∗of T;

(3)y∗is the unique fixed point of T in the set∆=

By using fixed point methods,we establish the generalized Hyers-Ulam-Rassias stability of the equation(1.3)in a fuzzy Banach space.Throughout this paper,assume that X is a vector space and(Y,N)is a fuzzy Banach space.

2　Generalized Hyers-Ulam-Rassias Stability of(1.3)

For a given mapping f:X→Y for x,y∈X,we define

We now investigate the generalized Hyers-Ulam-Rassias stability problem of the mixed functional equation(1.3)in a fuzzy Banach space.

Theorem 2.1Let s∈{1,−1},and φ:X×X→[0,∞]be a function such that there exists an L＜1 with

Let f be an even mapping satisfying f(0)=0 and

Then a unique quardratic mapping

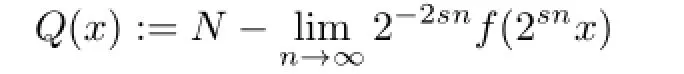
exists for each x∈X and Q:X→Y satisfies

Proof.Putting x=0 in(2.3),we see that

On the other hand,by replacing x by y in(2.3),we obtain

By two inequalities above,it follows

Let us first prove the case of s=1.

Consider the set

and introduce the generalized metric on S:

It is easy to show that(S,d)is complete,see the proof in[8].Now,we define a map J:S→S such that

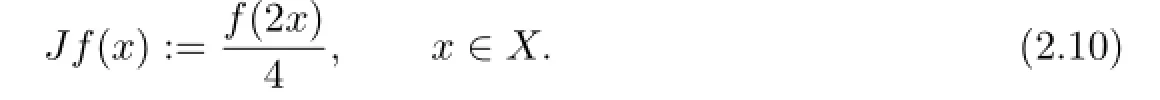
Let g,h∈S,and c∈[0,∞]be an arbitrary constant with d(g,h)=c.Then for x∈X and g,h∈S,we obtain

So d(g,h)=c implies that

This means

It follows from(2.7)that

By Theorem 1.1,there exists a mapping Q:X→Y satisfying

(1)Q is a fixed point of J,that is,

Since f is even,Q is even,too,the mapping Q is the unique fixed point of J in the set S.

This implies that Q is a unique mapping satisfying(2.13)such that there exists a c∈(0,∞) satisfying

(2)d(Jnf,Q)→0 as n→∞.This implies

Thus,

By(2.3),

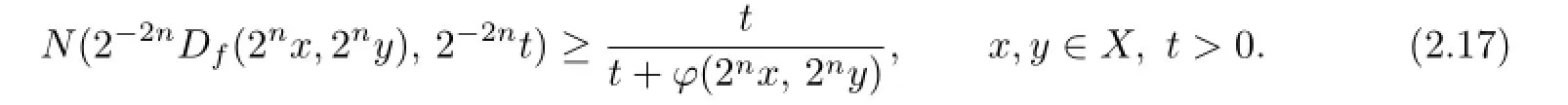
Replacing 2−2nt by t in(2.17),for all x,y∈X,t＞0 and all n∈N,we have

Since

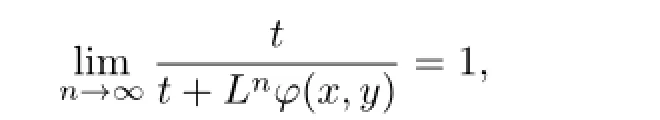
we obtain

Thus the mapping Q:X→Y is quadratic,as desired.

By(2.2),for all y∈X,t＞0,we have

Then the rest of proof is similar to the proof of the case of s=1,we can obtain the following inequality, in the left hand of(2.20),we get

and we can find the unique fixed point Q of J,which satisfies

Corollary 2.1Let θ＞0,and p be a real number with 0＜p＜2,X be a normed vector space with norm∥·∥.Let f be an even mapping satisfying f(0)=0 and

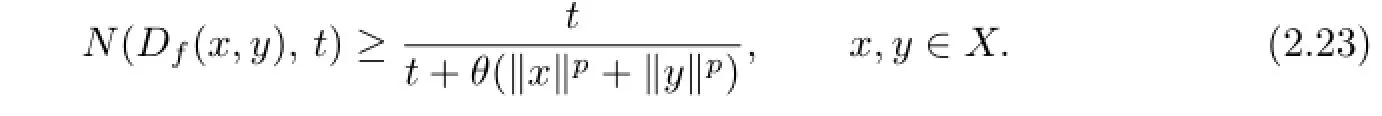
Then a unique quardratic mapping

exists for each x∈X and Q:X→Y satisfies

Proof.The proof follows from Theorem 2.1 by taking s=1 and φ(x,y):=θ(∥x∥p+∥y∥p) for all x,y∈X,we can choose by L=2p−2and we get the desired result.

Corollary 2.2Let θ＞0,p be a real number with p＞2,and X be a normed vector space with norm∥·∥.Let f be an even mapping satisfying f(0)=0 and

Then a unique quardratic mapping

exists for each x∈X and Q:X→Y satisfies

Proof.The proof follows from Theorem 2.1 by taking s=−1 and φ(x,y):=θ(∥x∥p+∥y∥p) for all x,y∈X,we can choose by L=22−pand we get the desired result.

Theorem 2.2Let s∈{1,−1}and φ:X×X→[0,∞]be a function such that there exists an L＜1 with

Let f be an odd mapping satisfying f(0)=0 and

Then a unique additive mapping

exists for each x∈X and A:X→Y satisfies

Proof.Putting x=0 in(2.3).For all x∈X,one has

Then by replacing x by 2y in(2.3),we obtain

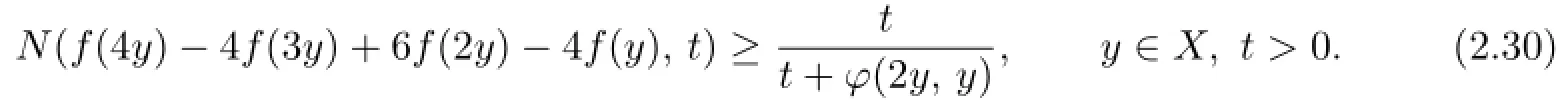
Combining(2.29)and(2.30),we lead to

Putting y:=x and g(x):=f(2x)−8f(x)for all x∈X,we obtain

Let us first prove the case of s=1.

Let the set(S,d)be the generalized metric space defined in the proof of Theorem 2.1, and define a map J:S→S as

Let g,h∈S such that d(g,h)=c.Then for all x∈X,g,h∈S,we obtain

So d(g,h)=c implies that the inequality d(Jg,Jh)≤Lc.This means

It follows from(2.7)that

By Theorem 1.2,there exists a mapping A:X→Y satisfying

(1)A is a fixed point of J,that is,A(2x)=2A(x)for all x∈X.Since f is odd,A is odd,too.The mapping A is the unique fixed point of J in the set S.This implies that A is a unique mapping satisfying(2.13)such that there exists a c∈(0,∞)satisfying

(2)d(Jng,A)→0 as n→∞.This implies

Thus,

By(2.3),we get

Then,for all x,y∈X,t＞0 and all n∈N,we have

Since

we obtain

Thus the mapping A:X→Y is additive,as desired.

It follows that

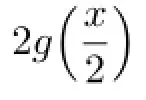
Combining above conclusion,we obtain

The rest of the proof is similar to Theorem 2.1.There exists a mapping A:X→ Y satisfying

Theorem 2.3Let s∈{1,−1},and φ:X×X→[0,∞]be a function such that there exists an L＜1 with

Let f be an odd mapping satisfying f(0)=0 and

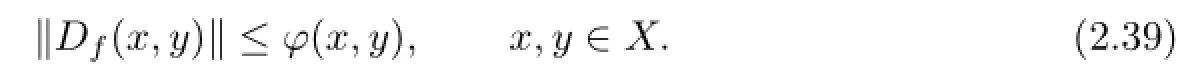
Then a unique cubic mapping

exists for each x∈X and C:X→Y satisfies

Proof.By(2.31),

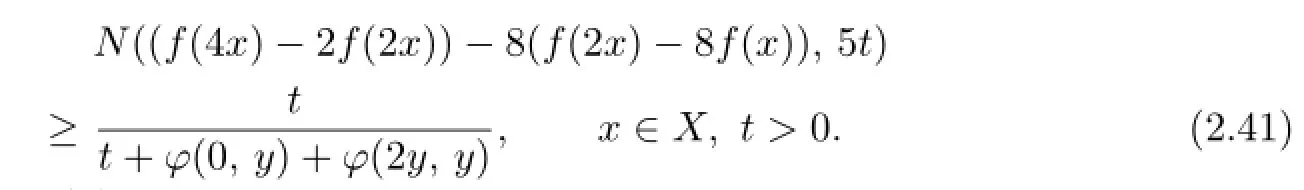
Let g(x):=f(2x)−2f(x)for all x∈X.Then we obtain

The rest proof is similar to Theorem 2.1.

[1]Ulam S M.A Collection of Mathematical Problems.New York:Interscience,1960.

[2]Hyers D H.On the stability of the linear functional equation.Proc.Nat.Acad.Sci.,1941,27: 222–224.

[3]Aoki T.On the stability of the linear transformation in Banach spaces.J.Math.Soc.Japan, 1950,2:64–66.

[4]Rassias J M,Semrl P.On the Hyers-Ulam stability of an approximately additive mappings.J. Math.Anal.Appl.,1993,173:325–338.

[5]Gˇavruta P.A generalization of the Hyers-Ulam-Rassias stability of approximately additive mappings.J.Math.Anal.Appl.,1994,184(3):431–436.

[6]Rassias J M.Solution of the Ulam stability problem for quartic mappings.Glasnik Matematiˇcki, 1999,34(2):243–252.

[7]Gotdji M E,Gharetapeh S K,Rassias J M,Zolfaghari S.Solution and stability of a mixed type additive,quadratic and cubic functional equation.Adv.Difference Equ.,2009,doi: 10.1155/2009/826130.

[8]Choonkil P.A fixed point approach to the fuzzy stability of an additive-quadratic-cubic functional equation.Fixed Point Theory Appl.,2009,doi:10.1155/2009/918785.

[9]Isac G,Rassias T M.Stability of φ-additive mappings:applications to nonlinear analysis.Int. J.Math.Math.Sci.,1996,19(2):219–228.

[10]Kenary H A.On the stability of a cubic functional equational equation in random normed spaces.J.Math.Extension.,2009,4(1):105–113.

10.13447/j.1674-5647.2016.02.05

date:Dec.8,2014.

The NSF(11101323)of China and the SRP(14JK1300)of Shaanxi Education Office.

E-mail address:chenglihua2002@126.com(Cheng L H).