Fixed Point Theorems of the Iterated Function Systems

JI YOU-QING,LIU ZHI,*AND RI SONG-IL

(1.School of Mathematics,Jilin University,Changchun,130012)

(2.Department of Mathematics,University of Science,Pyongyang,D.P.R.of Korea)



Fixed Point Theorems of the Iterated Function Systems

JI YOU-QING1,LIU ZHI1,*AND RI SONG-IL2

(1.School of Mathematics,Jilin University,Changchun,130012)

(2.Department of Mathematics,University of Science,Pyongyang,D.P.R.of Korea)

In this paper,we present some fixed point theorems of iterated function systems consisting of α-ψ-contractive type mappings in Fractal space constituted by the compact subset of metric space and iterated function systems consisting of Banach contractive mappings in Fractal space constituted by the compact subset of generalized metric space,which is also extensively applied in topological dynamic system.

fixed point,α-ψ-contractive mapping,iterated function system,generalized metric space

2010 MR subject classification:47H10,54H25

Document code:A

Article ID:1674-5647(2016)02-0142-09

1　Introduction and Preparatory Results

The most well known result in the theory of fixed points is Banach’s contraction mapping principle.Samet et al.[1]proved the theorem of existence of fixed point of an α-ψ-contractive mapping in complete metric space.They discussed the Banach contraction principle with some generalized contraction conditions and weakened the usual contraction condition.

A lot of generalizations of metric spaces exist.Most of them were introduced in an attempt to extend some fixed point theorems known from the metric case(see[2]–[4]). Hence a generalized metric space(g.m.s)has been defined as a metric space in which the triangle inequality is replaced by the quadrilateral inequality.Many researches have studied the fixed point theorem on the complete metric space(X,d),however,there are few results for the existence of fixed point on the complete metric space(H(X),h)with the use of fixed point theorem on(X,d)(see[5]–[9]).In general,even though f is ψ-contraction on(X,d), it cannot be concluded that Ffis ψ-contraction on(H(X),h).

The aim of this paper is to obtain the fixed point theorems of the some generalizedcontractions in metric space(H(X),h)and present the fixed point theorems of Banach contractions in metric space(H(X)∗,h∗).

Before we establish the fixed point theorems in metric space(H(X),h),we discuss some basic results.Samet et al.[1]proved the following results in the complete metric space.

Denote by Ψ the family of non-decreasing functions ψ:[0,+∞)→[0,+∞)such that＜+∞for each t＞0,where ψnis the n-th iteration of ψ.

Definition 1.1([1],Def.2.1)Let(X,d)be a metric space and f:X→ X be a given mapping.We say that f is an α-ψ-contractive mapping if there exist two functions α: X×X→[0,+∞)and ψ∈Ψ such that

for all x,y∈X.

If α(x,y)=1 for all x,y∈X and ψ(t)=kt for all t≥0 and some k∈[0,1),then f:X → X satisfies the Banach contraction principle.There is an example involving a function f that is not continuous(see[1],Example 2.4).

If α(x,y)=1 for all x,y∈X andfor all t＞ 0(not necessarilyfor all t＞0),then f:X → X satisfies a condition of the Matkowski’s contraction theorem(see[10],Th.1.6).

Definition 1.2([1],Def.2.2)Let f:X→X and α:X×X→[0,+∞).We say that f is α-admissible if for all x,y∈X,

Theorem 1.1([1],Th.2.1)Let(X,d)be a complete metric space and f:X→X be an α−ψ-contractive mapping satisfying the following conditions:

(1)f is α-admissible;

(2)There is an x0∈X such that α(x0,f(x0))≥1;

(3)f is continuous.

Then f has a fixed point,that is,there exists an x∗∈X such that f(x∗)=x∗.

To assure the uniqueness of the fixed point,we consider the following hypothesis:

(H)For all x,y∈X,there is a z∈X such that α(x,z)≥1 and α(y,z)≥1.

Theorem 1.2([1],Th.2.3)Adding condition(H)to the hypotheses of Theorem 1.1,we obtain uniqueness of the fixed point of f.

These fixed point theorems extended an earlier result of Banach’s contraction principle and these results are a substantial generalization of Matkowski’s fixed point theorem(see [5],[7]–[9]).

2　α-ψ-contractive Type Mappings and Iterated Function Systems

We now give the theorems of fixed point of the some generalized contractions in the complete metric space(H(X),h).

Let(X,d)be a metric space and H(X)the class of all nonempty compact subsets of X.That is,H(X)denotes the space whose points are the compact subsets of X,other than the empty set.Define

where d(x,B)=inf{d(x,y):y∈B}.Then d(A,B)is the distance from the set A to the set B for all A,B∈H(X).

Define h:H(X)×H(X)−→[0,+∞)by

The following result plays an important role in proving existence of fixed point theorem in (H(X),h).The metric space(H(X),h)is complete provided that(X,d)is complete(for details see[5],[7]–[9],[11]).The classical iterated function system(IFS)consists of a finite family of Banach contractions from X to itself.Then there is a unique nonempty compact invariant subset of X with respect to these contractions.In what follows,we extend this IFS by considering a family of α-ψ-contractions.

We assume that(X,d)is a complete metric space and f:X → X is a continuous mapping on(X,d)such that

where x∗∈A,y∗∈B.

Since f:X→X is a continuous mapping on(X,d),we can define Ff:H(X)→H(X) as follows:

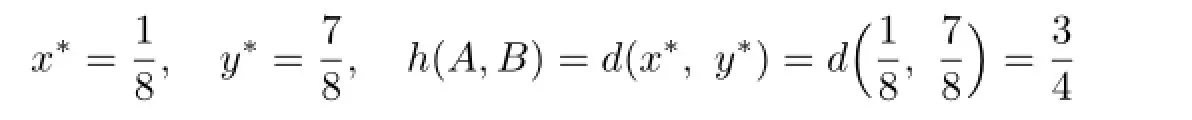
and

That is,for some A,B∈H(X),

Let α:X×X→[0,+∞)be a function.We define αα:H(X)×H(X)−→[0,+∞)by

If α(x,y)=1 for all x,y∈X,then

Lemma 2.1If f is α-admissible,then Ffis αα-admissible.

Proof.Let αα(A,B)≥1.Since αα(A,B):=inf{α(x∗,y∗)|d(x∗,y∗)=h(A,B),x∗∈A,y∗∈B}≥1,α(x∗,y∗)≥1.And since f is α-admissible,α(f(x∗),f(y∗))≥1.By the definition of f,

Hence

For all x∗∈A,y∗∈B such that d(x∗,y∗)=h(A,B),α(f(x∗),f(y∗))≥1.So

Therefore,if αα(A,B)≥1 for all A,B∈H(X),then αα(Ff(A),Ff(B))≥1,that is,Ffis αα-admissible.

Lemma 2.2Let f:X→X be a mapping.If there exists an x0∈X such that α(x0,f(x0))≥1,then there exists an A0∈H(X)such that αα(A0,Ff(A0))≥1.

Proof.Let A0:={x0}∈H(X).Then one has

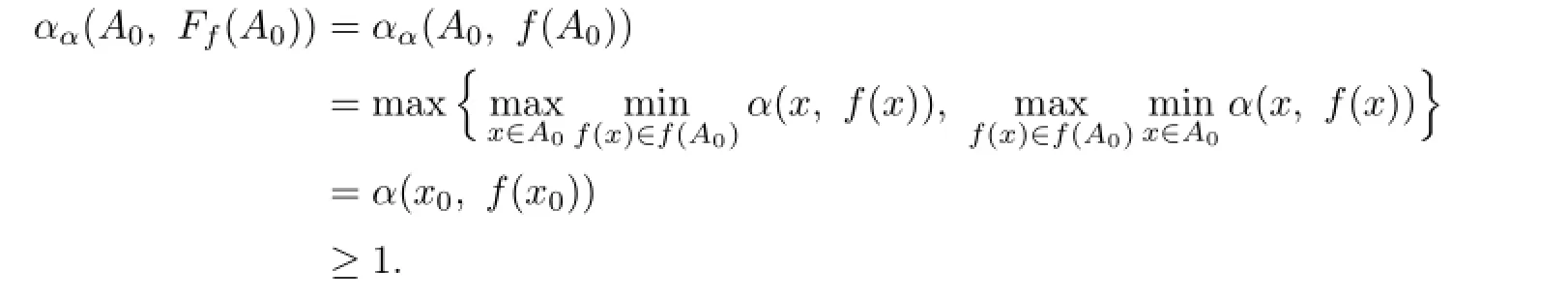
Lemma 2.3Let(X,d)be a complete metric space,ψ∈Ψ and f:X → X be an α−ψ-contractive mapping.Then

that is,Ff:H(X)→H(X)is αα−ψ-contractive(with the same function ψ).

Proof.Let A,B∈H(X).Then

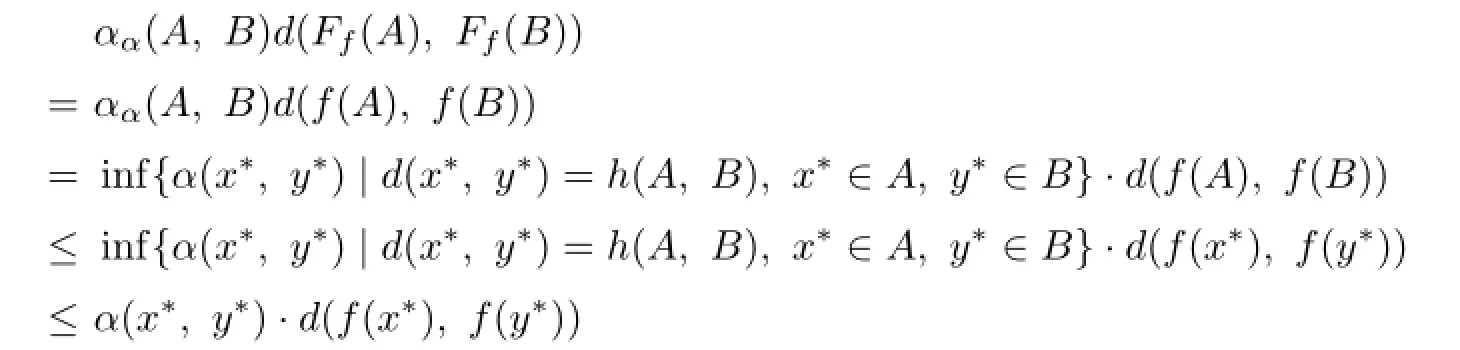
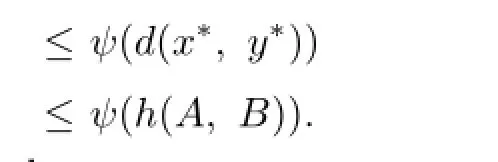
Similarly,

So

Theorem 2.1Let(X,d)be a complete metric space and f:X → X be an α-ψcontractive mapping satisfying the following conditions:

(1)f is α-admissible;

(2)there exists an x0∈X such that α(x0,f(x0))≥1.

Then the mapping Ff:A 7→ f(A)(A ∈H(X))is an αα-ψ-contraction(with the same function ψ)from H(X)into itself and Ffhas a fixed point,that is,there exists a K∈H(X) such that Ff(K)=K.

Proof.(H(X),h)is a complete metric space(see[7]–[8])and by Lemmas 2.1,2.2 and 2.3, Ff:H(X)→H(X)is an αα-ψ-contractive mapping satisfying the following conditions:

(1)Ffis αα-admissible;

(2)there exists an A0∈X such that α(A0,Ff(A0))≥1;

(3)Ffis continuous(by the definition of Ff).

Hence,by Theorem 1.1,Ffhas a fixed point,that is,there exists a K∈H(X)such that Ff(K)=K.This completes the proof.

In IFS{X,fi;i=1,2,...,n}on X,where fi:X → X is continuous,we define Ff1,...,fn:H(X)→H(X)by

The image of∅/=A⊂X under fiis given by

We consider the continuities that are meant in the Hausdorff sense.

(1)contraction,if there exists a Lipschitz constant 0≤L＜1 such that

(2)weak contraction,if there exists a comparison function ψ∈Ψ such that

(3)continuous on H(X),if for any A∈H(X)and ε＞0,there exists a δ(A,ε)＞0 such that for any B∈H(X)(h(A,B)＜δ(A,ε)),

Remark 2.1(1)If fifor all i=1,2,...,n is Banach contraction,thenis Banach contraction,too(see[8]).

(2)If fifor all i=1,2,...,n is weak contraction,thenis weak contraction, too(see[8]).

Now,we give a example involving a mapping Ff1,···,fn:H(X)→ H(X)that is not continuous.

Example 2.2Consider the functions

It is clear that

Since

for x/=0,one has

and

So for fixed x＞0,we have

and

The next theorem provides an important method for combining contraction mappings on(H(X),h)to produce new contraction mappings on(H(X),h).

Theorem 2.2Let(X,d)be a complete metric space and fi:X→X,i=1,2,···,n,be α-ψ-contraction mappings satisfying the following conditions:

(1)fiis α-admissible for all i=1,2,···,n;

(2)There exists an x0∈X such that α(x0,fi(x0))≥1 for all i=1,2,···,n.

Proof.We demonstrate the claim for n=2.By an inductive argument,we can complete the proof.

Let A,B∈H(X).By Lemma 2.3,one has

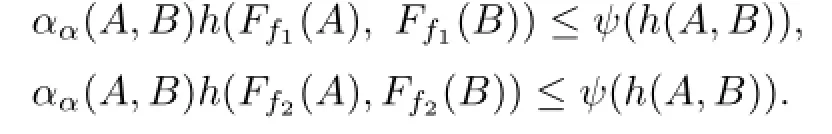
Because for A,B,C,D∈H(X),h(A∪B,C∪D)≤max{h(A,C),h(B,D)}(see[5]and [11]),and

So Ff1,f2is αα-admissible(cf.proof of the Lemma 2.1).Hence the result of this theorem follows from the Theorem 1.1.

Corollary 2.1Let(X,d)be a complete metric space and fi:X→X,i=1,2,···,n, be αi-ψi-contraction mappings satisfying the following conditions:

(1)fiis αi-admissible for i=1,2,···,n;

(2)There exists an x0∈X such that αi(x0,fi(x0))≥1 for i=1,2,···,n.

3　Iterated Function Systems in Generalized Metric Space

The following definition was given by Branciari(cf.[2]–[4]).

Definition 3.1Let X be a nonempty set and d∗:X×X→[0,+∞)be a mapping such that for all x,y∈X and all distinct points u,v∈X,each distinct from x,y: (1)d∗(x,y)=0 if and only if x=y; (2)d∗(x,y)=d∗(y,x);

(3)d∗(x,y)≤d∗(x,u)+d∗(u,v)+d∗(v,y).

Then(X,d∗)is called a generalized metric space(g.m.s.for short).

Convergent and Cauchy sequences in g.m.s.,completeness,as well as open ballscan be introduced in a standard way.However,the examples in[3]show several possible properties of generalized metrics,different than in the standard metric case.As shown in [2],a sequence in a g.m.s.may have two limits.

We denote{y∈X;d∗(x,y)＜r}for x in a g.m.sThe counterexample of[3]shows that:

(2)d∗needs not to be continuous in each of the coordinates;

(3)a g.m.s needs not to be a Hausdorff space.

A sequence in a g.m.s.may have two limits,however,there is a special situation.

Lemma 3.1([2],or[4],Lemma 1)Let(X,d∗)be a g.m.s.and{xn}be a Cauchy sequence in X such that xm/=xn,whenever m/=n.Then{xn}can converge to at most one point.

Note that we neither assume that the space(X,d∗)is Hausdorff,nor that the mapping d∗is continuous.

Lemma 3.2([4],Theorem 1.3)Let(X,d∗)be a Hausdorff and complete g.m.s.,and f:X → X be a self-map.If,for some λ∈(0,1),d∗(f(x),f(y))≤λd∗(x,y)holds for all x,y∈X(such a mapping is called a contraction mapping on X and λ is called the contractive constant of f),then f has a unique fixed point,that is,f(z)=z.Moreover,for each x0∈X,the corresponding Picard sequence{xn}converges to z.

This means that we get the Banach contraction principle in generalized metric spaces, proved without the assumption that the space is Hausdorff and that the function d∗is continuous.

Let(X,d∗)be a g.m.s.and H∗(X)the class of all nonempty compact subsets of X. Define h∗:H∗(X)×H∗(X)−→[0,+∞)by

Lemma 3.3The metric space(H∗(X),h∗)is complete provided that(X,d∗)is complete.

Proof.By the definition of d∗and proof process of the completeness of the space of fractal (see Theorem 1 in[11]),it is obvious.

Lemma 3.4Let(X,d∗)be a Hausdorff and complete g.m.s.,and f:X → X be a Banach’s contraction map in a g.m.s.,that is,for some λ∈(0,1),

Then the mapping Ff:A 7→f(A)(A∈H∗(X))is a λ-contraction(with the same λ)from H∗(X)into itself and Ffhas a unique fixed point and there exists K ∈H∗(X)such that Ff(K)=K.

Proof.See the proof of Lemma 3 in[11].

Now we obtain the following theorem.

Theorem 3.1Let(X,d∗)be a Hausdorff and complete g.m.s.,and fi:X → X be Banach’s contraction maps in a g.m.s.,i=1,2,···,n,that is,for some λi∈(0,1),

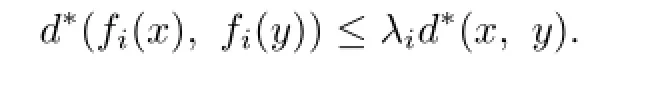
Thenis a Banach’s contractive map in a g.m.s. from H∗(X)into itself,that is,for all A,B∈H∗(X),

ProofFor A,B,C,D∈H∗(X),one has

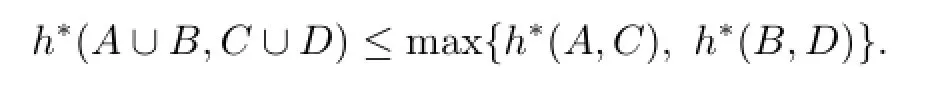
By Lemmas 2.3 and 3.4,it is easy to get the conclusion of this theorem.

Further,iterated function systems consisting of generalized α-ψ-contractive type mappings(see[10]),iterated function systems consisting of α-ψ-contractive type mappings in generalized metric space,and iterated function systems consisting of generalized α-ψcontractive type mappings in generalized metric space have been extensively studied by us and will be communicated in a forthcoming paper.

[1]Samet B,Vetro C,Vetro P.Fixed point theorems for α-ψ-contractive type mappings.Nonlinear Anal.,2012,75:2154–2165.

[2]Kadelburg Z,Radenovi´c S.Fixed point results in generalized metric spaces without Hausdorff property.Math.Sci.,2014,8(2),Article 125,8 pp.

[3]Samet B.Discussion on“A fixed point theorem of Banach-Caccioppoli type on a class of generalized metric spaces”by A.Branciari.Publ.Math.Debrecen,2010 76(3/4):493–494.

[4]Sarma I R,Rao J M,Rao S S.Contractions over generalized metric spaces.J.Nonlinear Sci. Appl.,2009,2(3):180–182.

[5]Lukawska G G,Jachymski J.The Hutchinson-Barnsley theory for infinite iterated function systems.Bull.Austral.Math.Soc.,2005,72(3):441–454.

[6]M´at´e L.The Hutchinson-Barnsley theory for certain noncontraction mappings.Period.Math. Hungar.,1993,27(1),21–33.

[7]Secelean N.Generalized iterated function systems on the space l∝(X).J.Math.Anal.Appl., 2014,410(2):847–858.

[8]Strobin F.Attractors of generalized IFSs that are not attractors of IFSs.J.Math.Anal.Appl., 2015,422(1):99–108.

[9]Strobin F,Swaczyna J.On a certain generalisation of the iterated function system.Bull. Austral.Math.Soc.,2013,87(1):37–54.

[10]Amiri P,Rezapour Sh,Shahzad N.Fixed points of generalized α−ψ contractions.Rev.R. Acad.Cienc.Exactas Fis.Nat.Ser.A,Math.,2014,108(2):519–526.

[11]Barnsley M F.Fractals Everywhere.New York:Academic Press,1988.

10.13447/j.1674-5647.2016.02.07

date:April 24,2015.

The NSF(11271150)of China and China Government Scholarship.

.

E-mail address:jiyq@jlu.edu.cn(Ji Y Q),liuzhi10@mails.jlu.edu.cn(Liu Z).