On Integrable Conditions of Generalized Almost Complex Structures

YIN YAN-BINAND LIU LING

(1.School of Mathematics and Statistics,Henan University,Kaifeng,Henan,475004)

(2.School of Applied Science,Beijing Information Science and Technology University, Beijing,100192)

Communicated by Rong Xiao-chun



On Integrable Conditions of Generalized Almost Complex Structures

YIN YAN-BIN1AND LIU LING2

(1.School of Mathematics and Statistics,Henan University,Kaifeng,Henan,475004)

(2.School of Applied Science,Beijing Information Science and Technology University, Beijing,100192)

Communicated by Rong Xiao-chun

Generalized complex geometry is a new kind of geometrical structure which contains complex and symplectic geometry as its special cases.This paper gives the equivalence between the integrable conditions of a generalized almost complex structure in big bracket formalism and those in the general framework.

generalized almost complex geometry,big bracket,supermanifold

2010 MR subject classification:53D17,17B63

Document code:A

Article ID:1674-5647(2016)02-0111-06

1　Introduction

Generalized geometry was created by Hitchin[1]originally as a way of characterizing special geometry in low dimensions,and has been further developed by Hitchin’s students.

In[2],the integrable conditions under which a generalized almost complex structure becomes a generalized complex structure have been given in general way.The same question is discussed by using the big bracket formulism in supermanifold geometry by Kosmann-Schwarzbach and Rubtsov[3].

In this paper,we firstly recall some basic notions and facts about generalized complex structures,and then we devote to proving the equivalence between the integrable conditions of a generalized almost complex structure in different formalism.

2　Integrable Conditions of Generalized Almost Complex Structures

Assume that M is a real manifold with dimension 2n and set TM=TM ⊕T∗M.A generalized almost complex is an endomorphism N:TM−→TM such that

(1)N is symplectic,i.e.,〈Ne1,e2〉+〈e1,Ne2〉=0 for e1,e2∈Γ(TM);

(2)N is complex,i.e.,N2=−Id,

where〈·,·〉denotes the natural pairing given by〈X+ξ,Y+η〉=η(X)+ξ(Y)for X+ξ,Y+η∈Γ(TM).

Any generalized almost complex structure N may be presented by classical tensor fields as follows:

where π∈Γ(∧2TM),σ∈Ω2(M),and N is a(1,1)-tensor field over M,π♯:T∗M−→TM denotes a linear map defined by π♯(ξ)=iξπ=π(ξ,·)for ξ∈Ω1(M).Similarly,σ♯is a linear map defined by σ♯(X)=iXσ for X∈Γ(TM),N∗is the dual map of N.Clearly,N is symplectic if N is of the above form.

For any e=X+ξ∈Γ(TM),we have

This structure is described by the big bracket formulism in[3].The big bracket,denoted by{·,·},is an even graded bracket on the space O of functions on the cotangent bundle ΠT∗M,which is a supermanifold given by TM,more details are found in[4]–[5].The action of N on e∈Γ(TM)can be expressed as

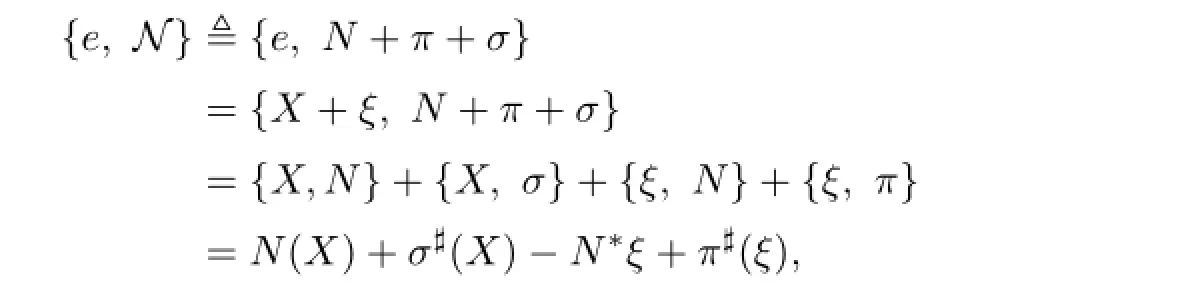
that is,Ne={e,N}for any e∈Γ(TM).

By definition of the generalized almost complex structure,the endomorphism N=N+ π+σ of TM is a generalized almost complex structure if and only if the following equalities hold:

(a)N2+π♯σ♯=−Id;

(b)Nπ♯=π♯N∗;

(c)σ♯N=N∗σ♯.

The Dorfman torsion of a generalized almost complex N,denoted by τµN,is defined by τµN(e1,e2)=[Ne1,Ne2]µ−N([Ne1,e2]µ+[e1,Ne2]µ−N[e1,e2]µ),e1,e2∈Γ(TM), where the bracket[·,·]µis the canonical Courant bracket on M defined by [X+ξ,Y+η]µ={{X+ξ,µ},Y+η}=[X,Y]µ+LXη−iYdξ,X+ξ,Y+η∈Γ(TM). More caculations can be found in[3].If we define

the torsion of N may be expressed as

Proposition 2.1[3]In terms of big bracket,we have

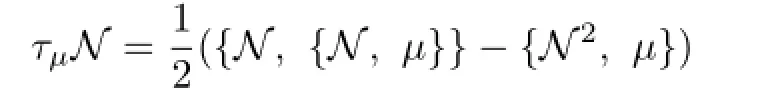
and

Definition 2.1A generalized almost complex structure N is a generalized complex structure if τµN=0.

Theorem 2.1[3]A generalized complex structure is a generalized almost complex structure N satisfying

Comparing their degrees of two sides of the equality(2.1),we obtain the following theorem.

Theorem 2.2A generalized almost complex structure N=π+σ+N is a generalized complex structure if and only if

(I1)[N,N]µ+[π,σ]µ+[σ,π]µ=µ;

(I2)[N,π]µ+[π,N]µ=0;

(I3)[N,σ]µ+[σ,N]µ=0;

(I4)[π,π]µ=0.

Theorem 2.1 describes the compatible conditions under which a generalized almost complex structure becomes a generalized complex structure.Those compatible conditions are given in big bracket formalism.But it can be rewritten as the following theorem in a general way.

Theorem 2.3A generalized almost complex structure N=π+σ+N is a generalized complex structure if and only if for X,Y,Z∈Γ(TM),ξ,η∈Ω1(M),

(J1)τµN(X,Y)=π♯(iX∧Ydσ);

(J2)N∗[ξ,η]π=Lπ♯(ξ)N∗η−Lπ♯(η)N∗ξ−d(π(N∗ξ,η));

(J3)dσN(X,Y,Z)=dσ(NX,Y,Z)+dσ(X,NY,Z)+dσ(X,NY,Z)+dσ(X,Y,NZ), where σN(X,Y)=σ(NX,Y);

(J4)π♯[ξ,η]µ=[π♯(ξ),π♯(η)]µ.

Proof.Since N is complex,we have

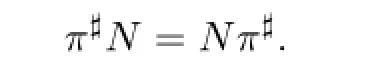
Consider

It shows that{π,N}is a bivector from its bi-degree(2,0).Thus,πNis a bivector field and

Proof.Note that

Moreover,

and

Hence

which shows that

Furthermore,we can get

since N is complex.

Proof of Theorem 2.3We hope to prove that the integrable conditions in Theorem 2.2 are one-to-one equivalent corresponding to the integrable conditions in Theorem 2.3.

For the first condition,assume that

Then we have

Hence,τµN={dσ,π},and for X,Y∈Γ(TM),we have

Thus,

For the second condition,consider

Applying the second condition[π,N]µ+[N,π]µ=0 in Theorem 2.2,we have

and for any ξ,η∈Γ(T∗M),

Hence,

For the third condition,consider

Applying the third condition[N,σ]µ+[σ,N]µ=0,we obtain

Moreover,we have

Therefore,

The equivalence between the last compatible conditions in two theorems is obviously.

Remark 2.1Theorem 2.3 can be directly obtained in a general framework of Lie algebroids(see[2]).

[1]Hitchin N.Generalized calabi-yau manifolds.Q.J.Math.,2003,54(3):281–308.

[2]Crainic M.Generalized complex structures and Lie brackets.Bull.Braz.Math.Soc.,2011,42(4): 559–578.

[3]Kosmann-Schwarzbach Y,Rubtsov V.Compatible structures on Lie algebroids and Monge-Ampere operators.Acta Appl.Math.,2010,109(1):101–135.

[4]Yin Y B,He L G.Dirac strucures on protobialgebroids.Sci.China Ser.A,2006,49(10):1341–1352.

[5]Roytenberg D.On the Structure of Graded Symplectic Supermanifolds and Courant Algebroids. in:Quantization,Poisson Brackets and Beyond.Contemp.Math.vol.315.Providence,RI: Amer.Math.Soc.,2002:169–185.

10.13447/j.1674-5647.2016.02.03

date:Sept.7,2014.

The Excellent Talent Program(2012D005007000005)of Beijing.

E-mail address:yyb@henu.edu.cn(Yin Y B).