Unstabilized Self-amalgamation of a Heegaard Splitting along Disks

LIANG LIANG,LEI FENG-CHUN AND LI FENG-LING

(School of Mathematical Sciences,Dalian University of Technology,Dalian,Liaoning,116024)



Unstabilized Self-amalgamation of a Heegaard Splitting along Disks

LIANG LIANG,LEI FENG-CHUN AND LI FENG-LING*

(School of Mathematical Sciences,Dalian University of Technology,Dalian,Liaoning,116024)

In this paper,we prove that a self-amalgamation of a strongly irreducible Heegaard splitting along disks is unstabilized.

Heegaard splitting,self-amalgamation,unstabilized

2010 MR subject classification:57N10,57M50

Document code:A

Article ID:1674-5647(2016)02-0117-05

1　Introduction

So a natural question is when is an amalgamation of two unstabilized Heegaard splittings unstabilized?A well-known result is the Gordon conjecture:The connected sum ofunstabilized Heegaard splittings is never stabilized(see[2],Problem 3.91).This was proved independently by Bachman[3]and by Qiu and Scharlemannin[4].When the genus of the amalgamated surface is positive,there exist many counterexamples showing that an amalgamation of two unstabilized Heegaard splittings might be stabilized(see[5]–[8]).On the other hand,many sufficient conditions for an amalgamation of two unstabilized Heegaard splittings to be unstabilized are given,see[9]–[12],where the gluing maps are required to be complicated enough,and[13]–[15],where the the factor Heegaard splitings are of“high”distance.

Let M be a self-amalgamation ofalong boundary components F1and F2ofGiven a Heegaard splittingforthere is amalgamated Heegaard splittiing for M, obtained by an analogous construction to that of Schulten’s.It has been proved by Du and Qiu[16]that the self-amalgamation of a“high”distance Heegaard splitting is unstabilized. Recently,Zou et al.[17]proved that the self-amalgamation of a Heegaard splitting of distance at least 3 is unstabilized.In[18],we generalize the self-amalgamation of a Heegaard splitting to the case where the amalgamated surface could be with nonempty boundaries.And we proved that if the Heegaard splitting is strongly irreducible and annulus-busting,then any self-amalgamation of the Heegaard splitting along any essential subsurfaces is unstabilized.

In this paper,we consider a special case when the amalgamated surface is a disk.We prove that the self-amalgamation of a strongly irreducible Heegaard splitting along two disjoint disks is unstabilized.The article is organized as follows:in Section 2,we review some necessary preliminaries.The statement and proof of the main result is given in Section 3.

2　Preliminary

Let M be a compact orientable 3-manifold and F be a properly embedded surface in M. F is said to be compressible if either F is a 2-sphere which bounds a 3-ball or there is an essential simple closed curve on F which bounds a disk in M;otherwise,F is said to be incompressible.F is said to be essential if F is incompressible and no component of F is∂-parallel in M.A simple closed curve in F is said to be essential if it is not contractible or∂-parallel in F.

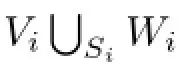
3　Main Result and Proof

Proof.By the definition of self-amalgamation,the self-amalgamated surfaces lie in the same side of the Heegaard surface.So we assume that F1and F2are two disjoint disks in∂−W and f is a homeomorphism from F1to F2just as above.

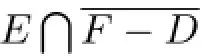
A compression body is called simple if there is only one essential separating or nonseparating disk up to isotopy.Then we have the following corollary:

[1]Schultens J.The classification of Heegaard splittings for(compact orientable surface)×S1. Proc.London Math.Soc.,1993,67(2):425–448.

[2]Kirby R.Problems in low-dimensional topology.Algebr.Geom.Topol.,1978,32:273–312.

[3]Bachman D.Connected sums of unstabilized Heegaard splittings are unstabilized.Geom. Topol.,2008,12:2327–2378.

[4]Qiu R F,Scharlemann M.A proof of the Gordon conjecture.Adv.Math.,2009,222(6):2085–2106.

[5]Bachman D,Derby-Talbot R.Degeneration of Heegaard genus,a survey.Geom.Topol. Monogr.,2007,12:1–15.

[6]Bachman D,Schleimer S,Sedgwick E.Sweepouts of amalgamated 3-manifolds.Algebr.Geom. Topol.,2006,6:171–194.

[7]Kobayashi T,Qiu R F,Rieck Y,Wang S C.Separating incompressible surfaces and stabilizations of Heegaard splittings.Math.Proc.Cambridge Philos.Soc.,2004,137:633–643.

[8]Schultens J,Weidmann R.Destabilizing amalgamated Heegaard splittings.Geom.Topol. Monogr.,2007,12:319–344.

[9]Lackenby M.The Heegaard genus of amalgamated 3-manifolds.Geom.Dedicata,2004,109: 139–145.

[10]Li T.On the Heegaard Splittings of Amalgamated 3-manifolds.in:Geom.Topol.Monogr.vol. 12.Coventry:Geom.Topol.Publ.,2007.

[11]Li T.Heegaard surfaces and the distance of amalgamation.Geom.Topol.,2010,14:1871–1919.

[12]Souto J.Distance in the curve complex and Heegaard genus,preprint.

[13]Du K,Gao X T.A note on Heegaard splittings of amalgamated 3-manifolds.Chinese Ann. Math.Ser.B,2001,32:475–482.

[14]Kobayashi T,Qiu R F.The amalgamation of high distance Heegaard splittings is always efficient.Math.Ann.,2008,341:707–715.

[15]Yang G Q,Lei F C.Amalgamations of Heegaard splittings in 3-manifolds without essential surfaces.Algebr.Geom.Topol.,2009,9:2041–2054.

[16]Du K,Qiu R F.The self-amalgamation of high distance Heegaard splittings is always efficient. Topology Appl.,2010,157:1136–1141.

[17]Zou Y Q,Du K,Guo Q L,Qiu R F.Unstabilized self-amalgamation of a Heegaard splitting. Topology Appl.,2013,160(2):406–411.

[18]Liang L,Lei F C,Li F L.A sufficient condition for a self-amalgamation of a Heegaard splitting to be unstabilized.Topology Appl.,2014,178:345–351.

[19]Casson A J,Gordon C McA.Reducing Heegaard splittings.Topology Appl.,1987,27:275–283.

10.13447/j.1674-5647.2016.02.04

date:Nov.24,2014.

The NSF(11101058,11329101 and 11471151)of China and the Fundamental Research Funds(DUT14ZD208 and DUT14LK12)for the Central Universities.

.

E-mail address:liang liang@aliyun.com(Liang L),dutlfl@163.com(Li F L).