Finitely Generated Torsion-free Nilpotent Groups Admitting an Automorphism of Prime Order

XU TAOAND LIU HE-GUO

(1.Department of Science,Hebei University of Engineering,Handan,Hebei,056038)

(2.Department of Mathematics,Hubei University,Wuhan,430062)

Communicated by Du Xian-kun



Finitely Generated Torsion-free Nilpotent Groups Admitting an Automorphism of Prime Order

XU TAO1AND LIU HE-GUO2

(1.Department of Science,Hebei University of Engineering,Handan,Hebei,056038)

(2.Department of Mathematics,Hubei University,Wuhan,430062)

Communicated by Du Xian-kun

Let G be a finitely generated torsion-free nilpotent group and α an automorphism of prime order p of G.If the map φ:G−→G defined by gφ=[g,α] is surjective,then the nilpotent class of G is at most h(p),where h(p)is a function depending only on p.In particular,if α3=1,then the nilpotent class of G is at most 2.

torsion-free nilpotent group,regular automorphism,surjectivity

2010 MR subject classification:20E36

Document code:A

Article ID:1674-5647(2016)02-0167-06

1　Introduction and Main Results

An automorphism of a group G is called regular if it moves every element of G except the identity.Burnside[1]proved the following classical result.

Proposition 1.1A finite group G admits a regular automorphism α of order 2 if and only if G is abelian of odd order.

In Proposition 1.1,the condition on the finite groups is essential because Proposition 1.1 is incorrect for infinite groups.For example,let F be a free group generated by x and y, the automorphism α defined by xα=y and yα=x is regular of order 2.But F is not an abelian group.

In Proposition 1.1,if α is an arbitrary automorphism of order 2 of a group G and the map φ:G−→G defined by gφ=[g,α]is surjective,we obtain the following proposition.

Proposition 1.2Let G be a group and α an automorphism of order 2 of G.If the map φ:G−→G(g 7−→[g,α])is surjective,then G is abelian.

Proof.Since φ is surjective,for any x∈G,there exists some g∈G such that

Moreover,

Thus,for any g1,g2∈G,we have

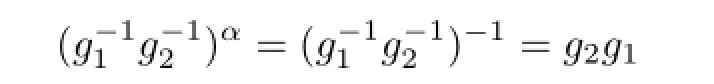
and

Obviously,g1g2=g2g1.Hence G is abelian.This completes the proof.

For a regular automorphism of order 3 of an arbitrary group,Neumann[2]proved the following result.

Proposition 1.3Let G be a group and α a regular automorphism of order 3 of G.If the map φ:G−→G(g 7−→[g,α])is surjective,then G is nilpotent of class at most 2.

For a regular automorphism of prime order of a finite group,Thompson[3]proved that if a finite group G has a regular automorphism of prime order,then G is nilpotent.For deeper results concerning regular automorphisms see[4].

Abandoning the condition on regularity,we are interested in the arbitrary automorphism of prime order of a group.In this paper,we study the arbitrary automorphism of order 3 of a finitely generated torsion-free nilpotent group,and obtain the following result which generalizes the above result of Neumann[2].

Theorem 1.1Let G be a finitely generated torsion-free nilpotent group and α an automorphism of order 3 of G.If the map φ:G−→ G(g 7−→ [g,α])is surjective,then the nilpotent class of G is at most 2.

Furthermore,we consider the automorphism of prime order p of a finitely generated torsion-free nilpotent group.

Theorem 1.2Let G be a finitely generated torsion-free nilpotent group and α an automorphism of prime order p of G.If the map φ:G−→G(g 7−→[g,α])is surjective,then the nilpotent class of G is at most h(p),where h(p)is a function depending only on p.

2　Proof of Theorem 1.1

Lemma 2.1Let G be a group and α an automorphism of order 3 of G.If the map φ:G−→G(g 7−→[g,α])is surjective,then for any x∈G,we have xxαxα2=1.

Proof.Since the map φ is surjective,for any x∈G,there exists some g∈G such that

Thus

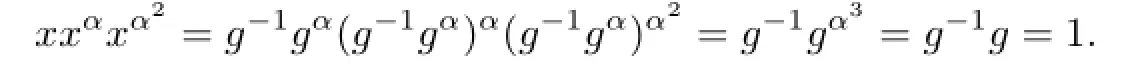
Lemma 2.2Let G be a finitely generated torsion-free nilpotent group and α an automorphism of order 3 of G.If the map φ:G−→G(g 7−→[g,α])is surjective,then the following results hold:

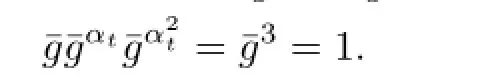
Since p/=3,it follows¯g=1,and thus αtis regular.

Lemma 2.3Let α be a regular automorphism of a group G.If the map φ:G −→G(g 7−→[g,α])is surjective,then αcgis a regular automorphism,where cgdenotes conjugation by g.

Proof.Since the map φ is surjective,for any g∈G,there exists some h∈G such that

Thus,for any x∈G,

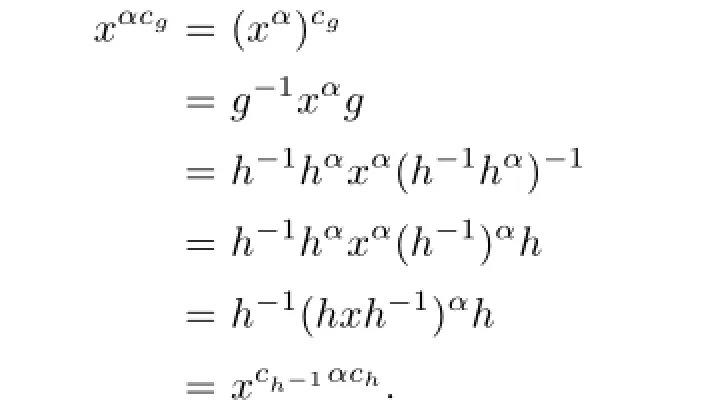
Hence

for some h∈G.Consider an element y∈G such that yαcg=y.We have

It follows that

Since α is regular,one has

Thus y=1,as required.

Proof of Theorem 1.1By Lemma 2.2(ii),for p/=3 and a positive integer t,admits a regular automorphism αtof order dividing 3.Putand observe that the mapis surjective.By Lemma 2.1,

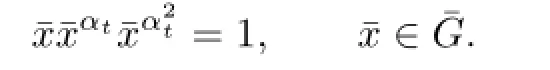
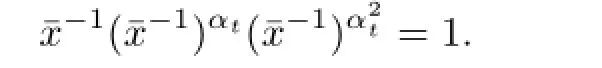
It follows

Hence

It follows

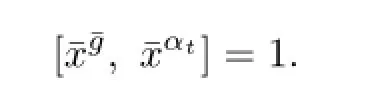
Similarly,

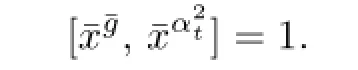
Namely,

It follows

since

Observing that

and

we obtain

and thus

3　Proof of Theorem 1.2

Lemma 3.1Let G be a group and α an automorphism of prime order p of G.If the map φ:G−→G(g 7−→[g,α])is surjective,then for any x∈G,we have

Proof.Since the map φ is surjective,for any x∈G,there exists some g∈G such that x=[g,α].Thus

Lemma 3.2Let G be a finitely generated torsion-free nilpotent group and α an automorphism of prime order p of G.If the map φ:G−→G(g 7−→[g,α])is surjective,then the following results hold:

(iii)For any positive integer t,the automorphism αtinduced by α onis regular.

Proof.(i)By the Theorem 5.2.21 in[5],G is a residually finite q-gro∩up for every prime q.Thus,for q/=p and positive integer t,is a finite q-group and

(ii)By Lemma 3.1,we have

Since q/=p,one has¯g=1,and thus αtis regular.

Namely,

It follows that the nilpotent class of G is at most h(p),where h(p)is a function depending only on p.

Applying Lemma 3.2 for q/=2 and Kov´acs’result in[6],we obtain the following corollary.

Corollary 3.1Let G be a finitely generated torsion-free nilpotent group and α an automorphism of order four of G.If the map φ:G−→G(g 7−→[g,α])is surjective,then the second derived subgroup G′′is included in the centre of G.

Proof.Choose q/=2.According to Lemma 3.2(iii),the finite nilpotent groupadmits a regular automorphism of order dividing 4.By Proposition 1.1 and Kov´acs’result in[6],the second derived subgroupis included in the centre of.It follows that

In other word,

This implies that

Consequently,

[1]Burnside W.Theory of Groups of Finite Order(Second Edition).New York:Dover Publications Inc.,1955.

[2]Neumann B H.Group with automorphisms that leave only the neutral element fixed.Arch. Math.,1956,7:1–5.

[3]Thompson J.Finite group with fixed-point-free automorphisms of prime order.Proc.Natl.Acad. Sci.USA,1959,45:578–581.

[4]Higman G.Groups and rings which have automorphisms without non-trivial fixed elements.J. London Math.Soc.(2),1957,32:321–334.

[5]Robinson D J S.A Course in the Theory of Groups(Second Edition).New York:Springer-Verlag,1996.

[6]Kov´acs L G.Group with regular automorphisms of order four.Math.Z.,1961,75:277–294.

10.13447/j.1674-5647.2016.02.09

date:March 9,2015.

The NSF(11371124)of China,the NSF(F2015402033)of Hebei Province,and the Doctoral Special Foundation(20120066)of Hebei University of Engineering.

E-mail address:gtxutao@163.com(Xu T).