动态自适应遗传算法在模拟电路中的应用
王硕
(漳州职业技术学院 电子工程系,福建漳州 363000)
动态自适应遗传算法在模拟电路中的应用
王硕
(漳州职业技术学院电子工程系,福建漳州363000)
针对在模拟电路设计中参数调整出现的问题,将模拟电路设计与遗传算法相结合,提出一种利用动态自适应遗传算法设计模拟电路的运放的方法。通过将运放参数融入到遗传算法的改进中,实现模拟电路中运放的参数最佳。
动态自适应遗传算法;运算放大器;模拟电路
随着大规模集成电路设计的不断发展和应用,数模混合电路结合仍然是设计的主流形式,该设计既节省空间,又可提升性能,但集成过程中,数字集成电路设计技术已相当成熟,模拟电路只占其中很小一部分,但其电路设计却存在着很大的问题(如运行时间长、电路复杂、功能单一等)。若要改善模拟电路这些弊端,需从模拟电路中常见的运算放大器入手。因此,设计一个功能强大、运算合理和各参数最优的运算放大器是弥补模拟电路缺陷的主要手段。
笔者提出了一种利用动态自适应的遗传算法来调整运算放大器所有目标的动态适应、快速搜索、最优选择设计方案:首先,将运算放大器的多个个体参数融入到自适应的遗传算法中;其次,利用加速策略进行动态调整;最后满足运算放大器的目标最佳。以此可提高模拟电路中的集成运算放大电路的运行速度和精度,而达到保护优秀个体、全面实现模拟电路中的运放电路功能的目的,该设计使集成运算电路变得更为简单,运行时间大大缩短。
1 动态自适应遗传算法简介及设计流程
遗传算法基本原理是对随机产生的原始群体,通过算子挑选的方法来选择性能良好的个体。对于良好的个体而言,其并未终止变异,而是继续进行个体交叉变异形成新的群体,再以此为基础,重新进行优化,直至满足要求为止。这种循环迭代方法,最终目的是选择和保护最优个体以实现动态自适应的优化。然而,这种算法也存在着一定缺陷,即在算子挑选过程中不对性能普通的个体进行处理,这就会出现普通算子破坏优质个体现象,从而影响全局最优解的获得,甚至会引起个体搜索速度受限。因此,本文通过改变交叉算子自适应遗传算法,设计了一种基于动态加速自适应的遗传算法,并将这种算法应用于模拟电路设计中,以此提高运算放大器运行的速度和处理的精度[1],设计流程如图1所示。
2 运算放大器电路优化设计与建模
2.1优化设计电路参数
因运算放大器电路参数较多,且使其能实现自动调节、快速运行满足电路性能的需求比较困难,通过电路优化设计运算放大电路的主要性能参数,可使其都达到动态的、自适应的、高速的电路性能指标。可见,选取合理的电路结构和设计参数是非常必要的。
以一个两级的运算放大器电路结构为例[2](如图2所示),参数设计过程中,选取在电路设计中难以合理确定的,且对目标函数有较大影响的参数作为设计的变量,设计过程对目标函数影响小的参数可根据原则预先设定。
根据上述设计变量的原则,图2所示运算放大电路所涉及到的初始参数有W1、L1、W2、L2、W3、L3、W4、L4、W5、L5、W6、L6、W7、L7、W8、L8、C、R等共18个, 因电路中M1、M2、M3、M4完全对称,故只需从W1到W4只需分析W1、L1、W3、L3即可,这样,初始参数剩下14个。目标参数有开环电压增益、增益带宽积、相位裕度、转换率、功率损耗、噪声和带宽等7个参数,其中功耗、噪声和带宽可预先设定,则其余目标参数与初始参数之间的函数关系式[3]。

图1 动态自适应遗传算法流程图
(1)
GB=gm1/2πCc,
(2)

(3)

(4)
其中,开环电压增益(Av)是用于提供闭环运放放大器的精度;增益带宽积(GB)是求解增益带宽积的公式;相位裕度(phase):表示运算放大器闭环工作情况下的稳定性,通常取值60;转换率(SR)表示运算放大器对电源电压的灵敏度。
以上公式集中反映了运算放大器初始变量与目标函数之间的复杂关系,参数较多,彼此间互相影响,故可用动态自适应的遗传算法进行优化设计。
2.2动态自适应遗传算法实现模拟电路设计2.2.1参数设计方案
优化设计的参数选取是基于一个二级的密勒补偿的集成运算放大器(如图2所示)。运放电路中共有一个补偿电阻、一个补偿电容和8个CMOS晶体管共有14个参数可供调整,根据自适应遗传算法,每个个体都应有一套配置参数,且这组参数是由一串二进制染色体串构成的,所有管子的长度要相等且搜索空间保持一致。下面将该想法应用到模拟电路设计中[4],具体方法如下:
所有个体染色体向量设为:
[W1L1W3L3W4L4W5L5W6L6W7L7W8L8RC] ,
因不同运算放大器性能指标不同,为保障每个个体搜索范围一致,要求晶体管长度不宜超过3 μm。第一级运算放大器中,对电路增益有决定性的参数是晶体管长度L1和L3,搜索范围设为1~10 μm。为使运算放大器中的每个晶体管工作在饱和区,还须设置晶体管宽长比,设定负载电容为5 pF,补偿电容为1.1 pF。
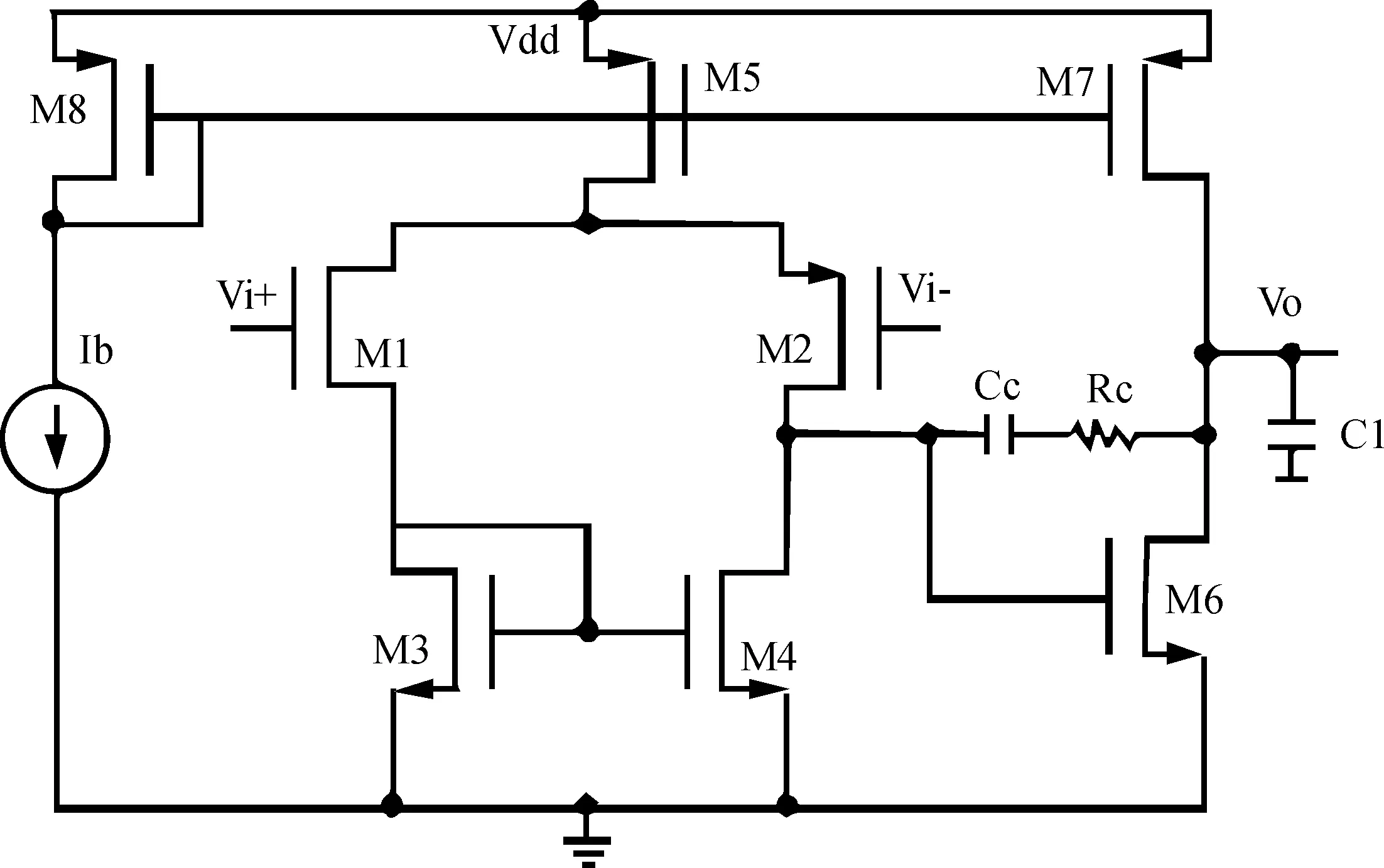
图2 二级运算放大器
2.2.2自适应函数选取
考虑到模拟电路中的运算放大器的多种性能指标,所以将其设置为自适应算法的多个目标参数。首先将多个目标参数进行优化,其次进行多目标的自适应调整,最后选取合适的自适应函数。这里,通过实际应用把所有个体目标加以整合,最终把这些目标转化为单个个体优化的目标,满足上述要求的函数如公式[5]:
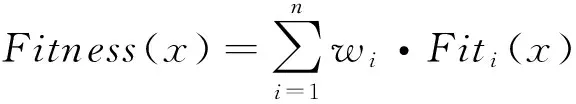
(5)
其中,wi为个体目标的权值系数,表示个体目标f(x)的重要程度;Fixi(x)为某目标x对个体目标f(x)的适应度函数,表示个体对其目标的归一化适应度;n为所要考虑的目标集合,Fitness为整合后的适应度函数。其中Fixi(x)为公式:

(6)
其中,1≤i≤m。根据人工神经网络的后向学习算法,将wi进行动态更新,满足自适应算法的自动调整特点。
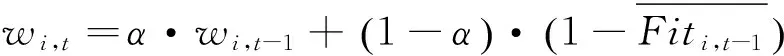
(7)
利用上述算法调整,可解决因各个个体目标性能参数不一引起的适应度函数贡献小的问题。根据适应度的大小调整,可采用最佳保留策略,满足条件的最佳个体参数直接传到下一代,从而避免自适应遗传算法过早收敛和搜索迟钝的现象。通过该方式,也可很好地满足这种电路结构的设计需求。
2.2.3动态加速策略
动态加速的遗传算法是在自适应的算法基础上,将自适应调整后的最佳个体的前N个变量变化区域作为一个新的个体进行调整,以此不断缩小搜索范围,实现动态的加速。但在实际过程中这并非单一问题。因为在加速过程中,最佳个体数目n的取值是随机的,当n的值较小时,最优解极易被排除;当n值较大时,最优解才会满足电路设计的需求。可见,最佳个体数量与收敛程度息息相关,何时加速和加速到何种程度直接决定全局最优解出现[6]。
在遗传算法中,影响最优解出现的是交叉算子(Pc)和变异算子(Pm)的设定[7]。对于运算放大器因无法确定最佳交叉算子和变异算子,引用动态加速过程,交叉算子和变异算子能动态快速适应变化。动态自适应遗传算法为了减少局部最优解的出现,分别对交叉算子和变异算子进行改进。具体方法如下:当各个个体目标参数适应度大体一致时,就通过提高Pc和Pm值来加速搜索;当各个个体目标适应度相差较大时,就通过降低Pc和Pm值来调节加速步调。由此可见,Pc和Pm的值变化可动态的调节搜索和收敛的速度,实现自适应的调整的目的[8]。在动态自适应的遗传算法中,Pc和Pm采用公式:

(8)
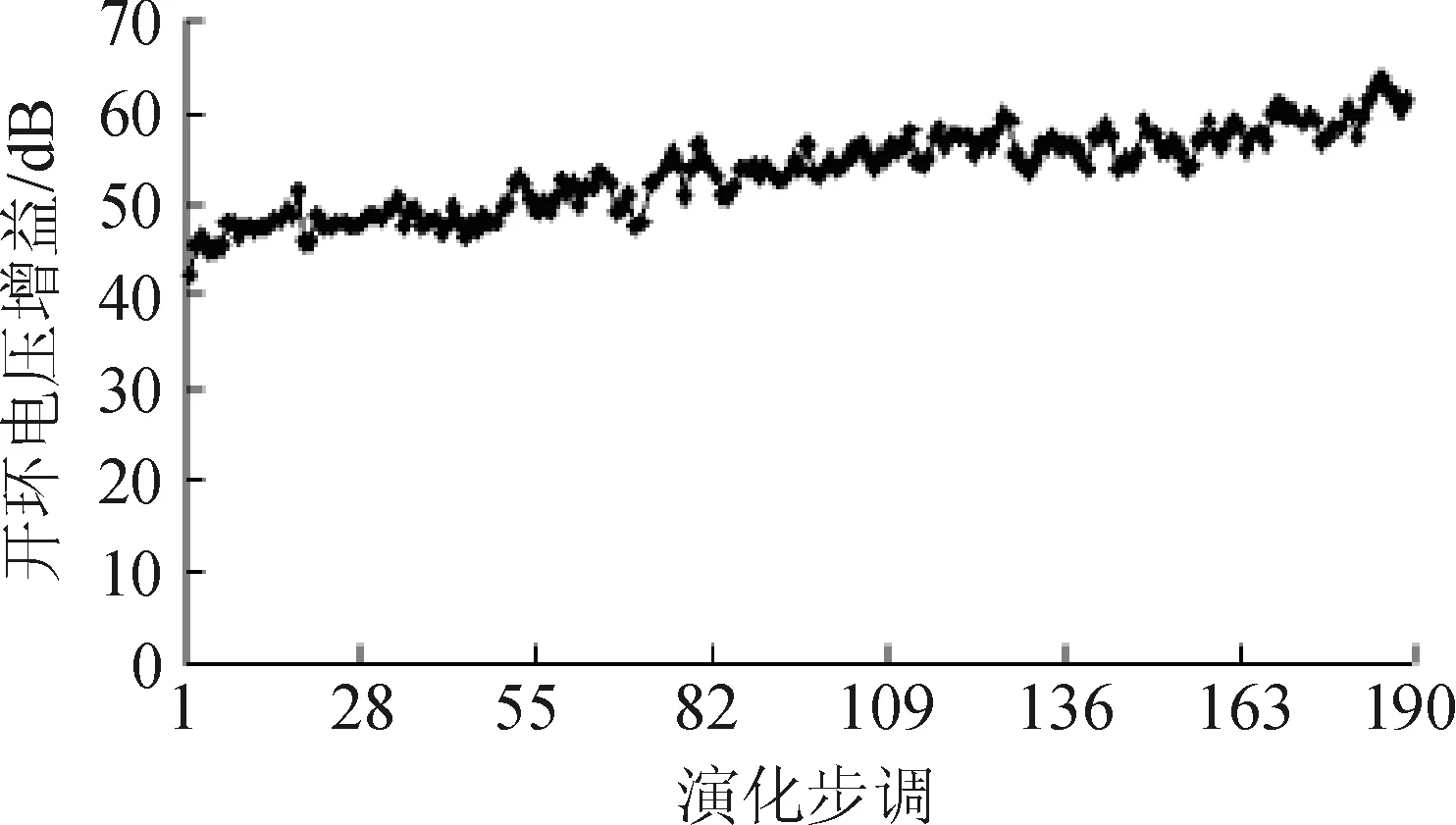
其中,0 (9) (10) 式中,fd(t)表示当前群体多样性的量度;fitmax(t)表示最大适应度,fitmin(t)表示最小适应度;α,k表示常数。根据公式可知,随着群体的个体多样性越高,fi(t)越小。在演变初期,群体的多样性起到主导作用,因而交叉率(Pc)和变异率(Pm)取值较大;随着运放过程进一步演化,收敛速度加快,交叉率和变异率也随之发生自适应调整,从而保证了最佳个体的出现。通过对交叉算子和变异算子改进,新一代个体发生循环式自适应调整,直至达到预期目标。此时,最大适应值所对应的解就是最佳设计变量组合,从而终止运算。 方案采用保留最优解的自适应遗传算法对两级运放进行实验仿真[9]。为使仿真结果具有一定说服力,设置模拟电路工作电压为2.5 V,补偿电容为2.5 pF,运行步调最大值200。通过软件仿真,验证模拟电路中的运算放大器的目标参数是否动态满足最佳设定需求。运行目标函数值如表1,软件仿真结果如图3~9所示。 图3 开环电压增益演变过程 性能要求仿真最小值最大值开环电压增益/dB>40504560增益带宽积/MHz>406040100相位裕度/(°)≈65706080带宽/MHz≈0.50.550.50.6功耗/mW<3.02.51.53.5噪声/(nV·Hz-1/2)<108106转换率/(V·us-1)>100250120280 图4 增益带宽积演化过程 图5 相位裕度演化过程图 图6 带宽演变过程法 图7 功耗演化进程 图8 噪声演化过程 图9 转换率演化进程 通过仿真波形,发现运算放大器的目标参数都满足给定的指标,且在动态范围可实现自动调整,所以,动态的自适应的遗传算法能够很好的实现模拟电路中的运算放大电路的设计,使其所有目标参数都能灵活的、快速的达到最佳状态。 通过上述分析,采用动态自适应的遗传算法实现模拟电路中的运算放大器设计,很好地解决了遗传算法中的过早收敛,搜索缓慢的弊端,极大地提高了优化算法的收敛速度和参数精度,保证了运算放大器最优解出现。 [1]赵曙光.基于多目标遗传算法的模拟电路进化设计方法[J].西安电子科技大学报,2004,31(3):342-346. [2]肖晗.基于遗传算法的模拟电路多目标设计[J].合肥工业大学学报,2008,31(7):1122-1123. [3]蓝天鸿,唐伟峰.基于自适应遗传算法的去耦电容自动选择[J].电子科技,2012,25(4):22-23. [4]毕查德·拉扎维.模拟 CMOS集成电路设计[M].西安交通大学出版社,2003:240-243. [5]丁敏,张永兴,王辉.动态自适应遗传算法在桩锚支护结构优化设计中的应用[J].建筑结构,2013,43(1):83-87. [6]陈立伟.自适应遗传算法的低噪声放大器设计[J].现代电子科技,2015,22(4):118-119. [7]黎钧琪,石国桢.遗传算法交叉率与变异率关系的研究[J].武汉理工大学学报,2003,27 (1):97-99. [8]秦贞良,张涛,刘艳平.基于自适应遗传算法多项式预失真技术研究[J].电子科技,2014,27(4):13-14. [9]王海波,宋星原,王文凯.动态加速自适应遗传算法的应用[J].水电能源科学,2008,26(6):54-57. [10]周林,娄寿春,赵杰.基于遗传算法的目标优化分配模型[J].系统仿真学报,2003,31(1):21-23. Dynamic Adaptive Genetic Algorithm in the Application of the Analog Circuits WANG Shuo (Department of Electronic Engineering, Zhangzhou Vocational Technical College, Zhangzhou 363000,China) In order to resolve the problems of parameter adjustment in analog circuit design, by combination of analog design with genetic algorithm, this paper proposes a dynamic adaptive genetic algorithm as the op-amp method of analog circuit design, so as to obtain the op-amp best parameters in analog circuit by adding the op-amp parameters to the improvement of the genetic algorithm. dynamic adaptive genetic algorithm; operational amplifier;analog circuit 2016-02-28 王硕(1977—),女,吉林农安人,硕士,讲师,主要从事电子通信研究。 TN722.7 A 1009-0312(2016)03-0016-05

3 验证结果



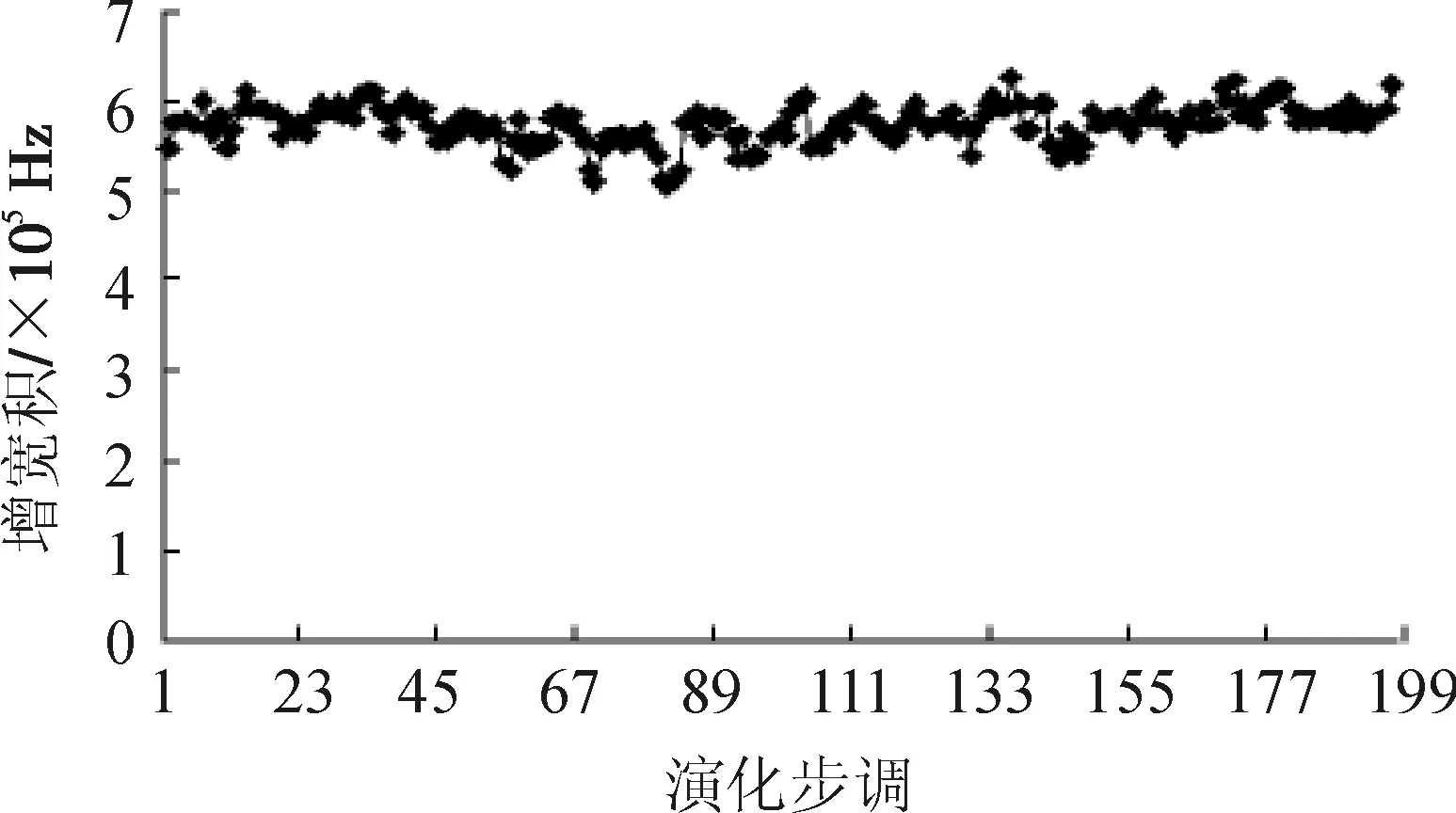

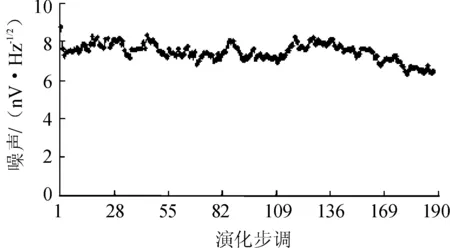

4 结语

