基于混沌算法的数字图像加密技术
刘羽飞
(韶关学院 物理与机电工程学院,广东韶关 512005)
基于混沌算法的数字图像加密技术
刘羽飞
(韶关学院物理与机电工程学院,广东韶关512005)
通过Logistic混沌映射产生混沌特性的序列,将混沌序列应用到数字图像加密解密技术中。混沌序列的值与数字图像灰度值进行了异或加密运算,后实现了改变数字图像灰度值,从而实现了数字图像的混沌加密。经过MATLAB仿真实现了加密的过程,仿真结果利用直方图,加密前后图像相邻像素值的相关性,密匙的安全性分析。表明了这种基于混沌算法的加密系统具有良好的安全性,快速性。
混沌;图像加密;Logistic映射
随着互联网和多媒体技术的快速发展,通过计算机网络传播图像,尤其在互联网、医疗、军事通信得到了广泛的应用,同时数字图像在传输过程中的安全性已经成为一个需要重点关注的问题。由于图像加密并不是简单的文本类型的加密,一些内在的图像属性如巨大的数据容量和高冗余,用传统的加密技术很难处理,针对图像加密是解决图像安全的关键技术,因此,研究图像加密具有很高的理论意义和现实价值[1-3]。目前,国内外对图像加密的方法主要有频域上的加密处理,利用各种频域的变换(如哈特莱变换、傅里叶变换、小波变换等),通过先将图像变换到频域,然后再对频域图像数据加密。近年来通过混沌算法对数字图像加密技术快速发展起来,该技术因数字图像加密后表现出的良好特性,得到了国内外大量的学者进行相关的研究和重视,并提出了多种基于混沌算法的图像加密技术[4-6]。笔者采用Logistic 映射产生混沌序列对数字图像进行加密处理,实现了数字图像的混沌加密。通过MATLAB的仿真实验表明这种加密算法且有较大的密匙空间,安全性较好,加密解密速度快[7-8]等优点。
1 图像加密系统
混沌现象的运动特征表现为有内随机性、遍历性、初值敏感性、有界性、轨道不稳定性与分岔等特性。由于混沌具有内随机特性和初值敏感性,轨道混合特性分别对应传统加密系统的混乱性和扩散特性,所以可以将混沌算法应用于数字图像加密系统。基于混沌算法的数字图像加密系统中,通常利用一维或者二维混沌映射产生的伪随机序列对数字图像像素值的位置进行混乱重置,扩散操作[4]。
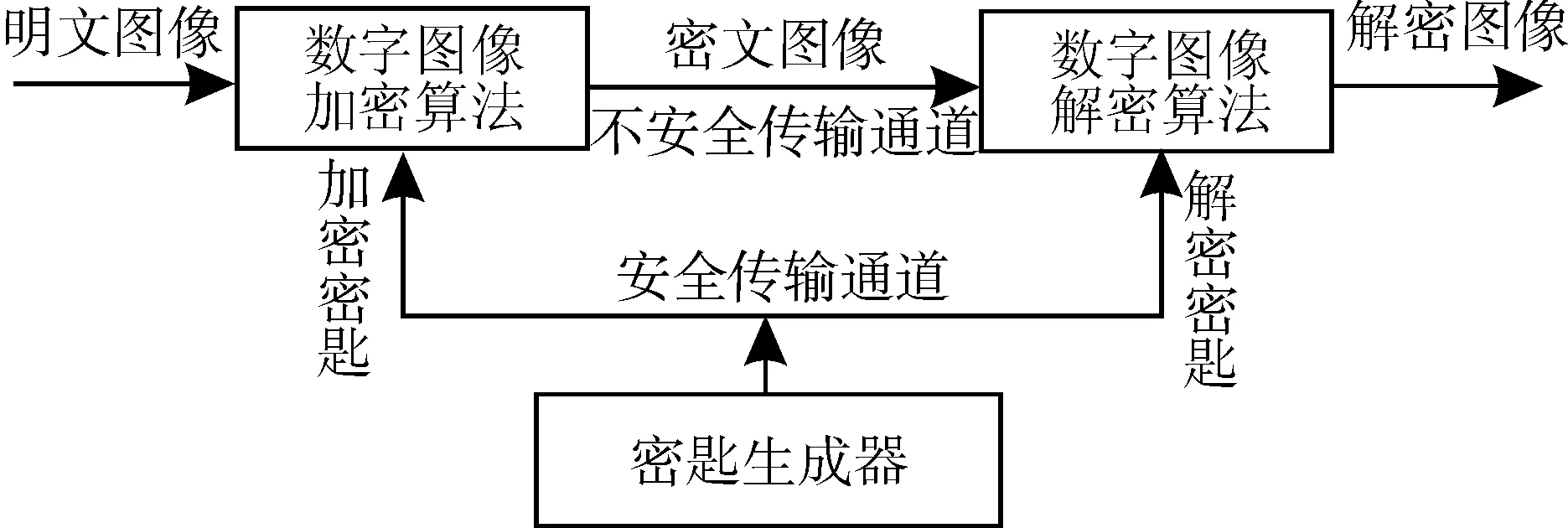
图1 图像加密系统

图2 加密流程
图1为一个数字图像加密系统结构简图。当系统输入明文图像,经过加密算法明文图像转换成密文图像,在加密算法中加入了加密密匙,密文经过加密后传输到解密端,通过解密算法和解密密匙将数字图像解密成明文图像,系统中将通过密匙生成器将加密密匙和解密密匙经过安全通道将密匙送到加密端和解密端。由于加密算法是公开的,算法的安全性就取决于密匙的安全性。图2为基于混沌加密系统的加密流程,加密的原始图像是初始输入的明文图像,加密系统的混沌加密密钥设置为混沌Logistic系统的参数。
2 混沌映射
在数字图像混沌加密系统中常用到多种混沌系统,这些混沌系统能清楚的表现出混沌的主要特征,且数学模型简单化,操作处理较易,较常用到的一维混沌映射有Logistic映射、Chebyshew映射等。
荷兰生物学家、数学家Verhulst在生态学的研究中,发现自然界的动物群体和自然环境有着相互的作用,他首先提出利用Logistic映射来描述自然界中生物群体数目随世代的变化。在19世纪中期提出的虫口动力模型,一维Logistic映射的数学表达式如下:
xn-1=μxn(1-xn) (n=1,2,3,…) ,
(1)
其中0≤xn≤1,μ为控制参数,0≤μ≤4。当μ的取值在0到4之间变化时,xn的状态值可分为周期区和混沌区。
Logistic混沌系统的运动轨迹呈现混沌状态,需具有一定的约束条件,即当初始值x1的值确定以后,任意给定一个初始控制参数μ,经过多次迭代后,都可以产生一个相应的数列,此时的数列并不一定是呈现出混沌状态的。实验数据表明,只有当3.569 945 6≤μ≤4时候,Logistic系统的运动轨迹才会呈现出混沌现象;当Logistic系统控制系数μ的值在[3.569 945 6,4]范围之间时,系统的迭代序列出现非周期、发散状态,此时对初值的选取有极小的差别都能呈现出明显不同的混沌效果,这就是初值选取的敏感性。由于Logistic混沌映射产生混沌序列的原理简单,同时该混沌映射具有良好的初值敏感性和非周期性,被广泛应用于多种加密系统中[9-11]。
3 仿真结果与分析
当选定初始值x1和控制参数μ后,将公式(1)经过多次迭代后,可以得序列X(1)、X(2)、X(3)、…,这个将是一个Logistic混沌映射序列。仿真平台为MATLAB,在MATLAB中可以看出当初值选定为x1=0.99和μ=3.999后,经过M*n次的迭代,N、M表示图像的大小,可以得到一个序列X(i),i=1,2,3,…,X(i)的取值范围都在0到1之间,通过该特性,可得到序列X(i)归一化到使其值在0到225之间得到序列xg(i)。因为图像的灰度值范围在0到255之间,所以需要将得到的混沌序列值进行归一化操作。接下来将得到的混沌序列xg(i)转换成图像大小的M*n的二维矩阵S。
图像加密的一次过程就是将加载后的图像X矩阵与混沌序列产生的二维矩阵进行异或操作,便可以得到一幅加密后的图像Y。密匙的初值就是所设置的x1=0.99和μ=3.999的值。解密过程就是加密过程的反向操作,通过反向操作后可得到解密图像。对图像加密效果可以如图3所示。
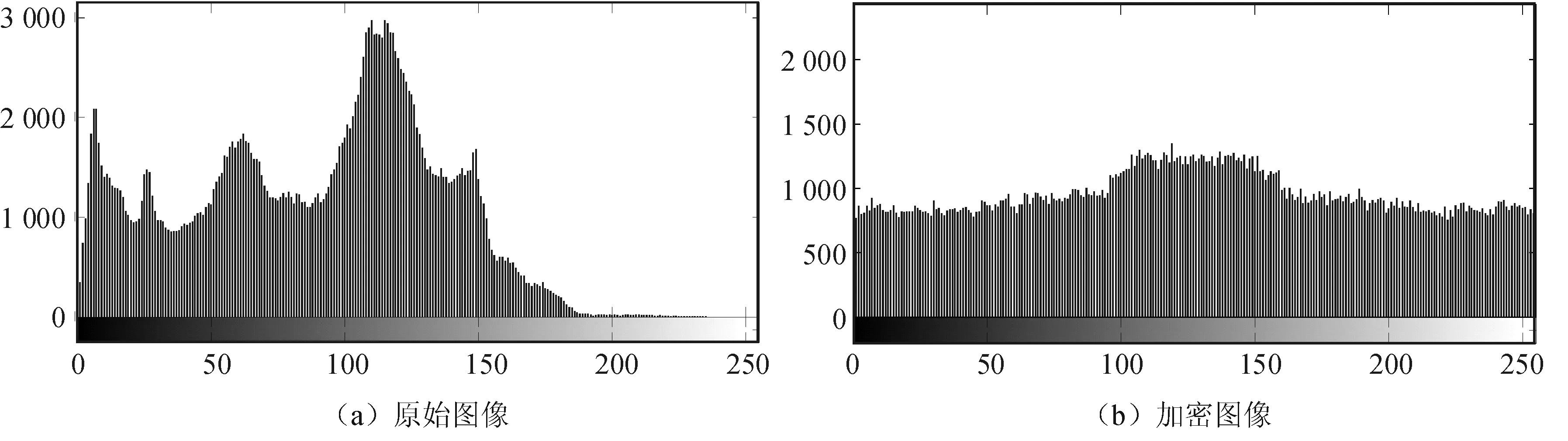
图4 直方图
图4是原始图像和加密图像的直方图,其中x轴表示灰度值从0到255,y轴表示图像中像素值分别在灰度值0~255之间的个数。通过两幅直方图对比分析可以明显看出原始图像的直方图像素值的分布非常散乱,不利于图像传输过程中的保密。经过混沌加密后的图像像素值分布更加均匀,加密图像的直方图具有更好的均匀特性,可以很好地掩盖原始图像像素值的分布规律。在原始图像中选取1 000个点进行水平的相关性分析发现,原始图像相邻像素值在水平方向上的相关达到0.980 2,同样选取加密图像中的1 000个像素点的值进行水平相关性分析,发现其水平方向相关性为0.026 9。从数据结果分析可以看出,原始图像的相邻象素值的相关系数较高趋近于1,经过混沌算法加密后的图像相邻象素值的相关系数非常低,接近于0,因此该方法可以有效地起到加密的作用,具有一定的抗攻击能力。
当解密的密匙与密匙有微小区别时,都解密不出原始图像。当密匙x1=0.99和μ=3.998时,μ只与正确密匙相差0.001,解密后图像如图5所示,解密后的图像完全没有原始图像所包含的图像信息,所以混沌数字图像加密方法具有极高的保密性。

图5 错误密匙解密图像
通过Logistic 混沌映射系统产生的一维混沌序列,将混沌序列对图像进行异或操作达到加密的目的。该加密方法所使用的加密密钥简单和加密过程通过混沌序列改变了原始图像的灰度值。从图像加密解密的实验仿真结果可以看出,该方法具有加密过程容易实现,加密速度快,保密性高,加密效果较好的特点。
[1]王静.混沌数字图像加密技术研究[D].南京:南京邮电大学,2013.
[2]Xiao D, Liao X F, Wei P C. Analysis and improvement of a chaos-based image encryption algorithm [J]. Chaos Solitons and Fractals, 2009, 40(5): 2192-2198.
[3]Kanso A, Ghebleh M. A novel image encryption algorithm based on a 3D chaotic map [J]. Communications in Nonlinear Science and Numerical Simulation,2012,17(7):2944-2959.
[4]黄慧青.基于混沌系统的图像隐藏技术[J].计算机系统应用,2013,22(11):183-186.
[5]任晓奎,马超.三维彩色图像加密的改进与实现[J].微电子学与计算机,2015,33(1):98-104.
[6]李巧君,张亚楠.基于混沌映射的图像快速加密改进算法[J].计算机测量与控制,2014,22(10):3270-3273.
[7]陈河山,吕珍珍,罗伟.一个基于离散混沌加密的数字水印算法[J].计算机科学,2014,41(12):48-52.
[8]张永红,张博.基于Logistic混沌系统的图像加密算法研究[J].计算机应用研究,2015,36(6):1770-1773.
[9]蔡苏亚. 基于相互迭代混沌算法实现数据加密及算法对比[J].现代电子技术,2015,38(2): 15-21.
[10]Pisarchik A N, Zanin M. Image encryption with chaotically coupled chaotic maps[J]. Physica D, 2008, 237(20): 2638-2648.
[11]胡铭.基于混沌系统的序列加密算法改进与应用研究[D].成都:成都理工大学, 2007.
Digital Image Encryption Techniques Based on Chaos Algorithm
LIU Yufei
(School of Physics and Mechanical and Electrial Engineering, Shaoguan University, Shaoguan 512005, China)
The chaotic sequence produced by Logistic chaotic mapping can be used to decrypt the digital image encryption technology. The value of the chaotic sequence and digital image grey value X or encryption are operated with a change of digital image grey value and a realization of digital image chaotic encryption. The results show that the encryption system based on chaos algorithm has good security and rapidity after the process of the encryption through MATLAB simulation, the usage of histogram as simulation results, the correlation of image adjacent pixels before and after encryption, and the analysis of key safety.
chaos; image encryption; Logistic mapping
2015-02-20
刘羽飞(1989—),男,广东韶关人,硕士,主要从事自动化检测装置及检测技术,数字图像处理研究。
TN91.73
A
1009-0312(2016)03-0021-03

