自适应切换双模盲均衡算法
曾乐雅 许 华 王天睿
自适应切换双模盲均衡算法
曾乐雅*①许 华①王天睿②
①(空军工程大学信息与导航学院 西安 710077)②(南京师范大学地理科学学院 南京 210046)
常数模算法在无线通信系统的盲均衡中得到广泛的使用,为了进一步降低稳态误差通常选择将其与判决引导最小均方误差算法相结合,传统的双模切换盲均衡算法通过人为设定门限值实现两种算法的硬切换,其切换时机选择的合理性无法保证,不能充分凸显双模切换的长处。该文利用凸组合结构借助遵循一定规则迭代变化的联合参数将两种算法进行结合,实现两种算法模式的切换,自适应地选择切换时机,并通过对算法的修正和混合参数归一化的改进使在克服恢复信号相位偏转的同时加快了收敛速率、降低了稳态误差;另外,对稳态性能进行推导分析得到了理论的稳态模型。仿真结果证明稳态性能与模型推导结果保持一致,参数归一化改进所得效果较为明显,与同类其它双模切换算法相比具有更优的性能。
信号处理;盲均衡;凸组合;双模;归一化
1 引言
在数字通信系统中,为了消除信道弥散而造成的符号间干扰(Inter-Symbol Interference, ISI)和信道间干扰(Inter-Channel Interference, ICI)通常采用自适应均衡技术。传统均衡技术通过发送训练序列实现均衡器权值系数的调整,而盲均衡由于不需要训练序列,可以用来解决第三方接收处理中的信道均衡问题,也可以用在合作接收中大幅度提升信道利用率。
常数模算法(Constant Modulus Algorithm, CMA)是盲均衡算法中一种经典、有效的算法之一,其因计算量少、易于实现等优点而被广泛使用。为了进一步提升常模算法的性能以及扩展其适用范围,相继提出了许多改进的常模算法,例如:基于QR分解的CMA算法[1],基于最大似然估计的CMA算法[2],基于非线性分数更新的CMA算法[3],基于方向梯度算法的CMA算法[4],基于余弦代价函数的CMA算法[5]等。尽管CMA算法可以稳定地收敛,但是其在稳态阶段仍然有很大的稳态误差导致误码率较高,尤其是对于非常数模信号。为了解决这个问题,有学者提出CMA算法与判决引导最小均方误差算法(Decision-Directed Least-Mean Square, DD-LMS)相结合的双模切换盲均衡算法,其实现方法为在收敛初期利用CMA算法冷启动特性和良好的收敛性能进行处理,而后转为利用DD-LMS算法进行均衡达到更优的效果。切换时机通常依赖于均方误差(Mean Squared Error, MSE)门限的选择,但是门限受到星座图、通信信道、信噪比等很多因素影响,很难找到最恰当的切换时机,这对系统均衡的性能有很大的影响。
为了克服在两种模式之间通过门限值的设定实现硬切换而造成性能下降的问题,提出了许多软切换方法,其性能有大幅度的提升,然而,这些方法的实现很大程度依赖于其中自适应盲均衡模式,不能充分反映其切换准则所带来的好处。近年来提出采用滤波器凸组合的方式来提高系统均衡的性能,该方法将两个不同设置、独立运行滤波器的结果进行混合,使得系统的整体性能在每次迭代中至少和性能较好的滤波器相同。凸组合方式受到了广泛的关注,并有许多相关的应用和改进,特别是在盲均衡中也有涉及[12]。尽管该结构的实现相比于单个CMA均衡器可以得到更低的稳态误差,但是其组成都是盲均衡滤波器,依然存在较大的剩余误差。
本文提出一种自适应切换的双模盲均衡结构,该结构将CMA算法和LMS算法的输出进行凸组合,盲均衡算法在初始收敛阶段或者信道发生突变后首先减小符号间干扰,然后当稳态MSE充分低时使整个系统工作在DD-LMS模式。因为两个均衡器并行连续不断地工作,且组合的方式以最大化系统性能为准则,因此本文提出的结构能够在CMA和LMS算法之间实现自适应切换。
2 盲均衡算法
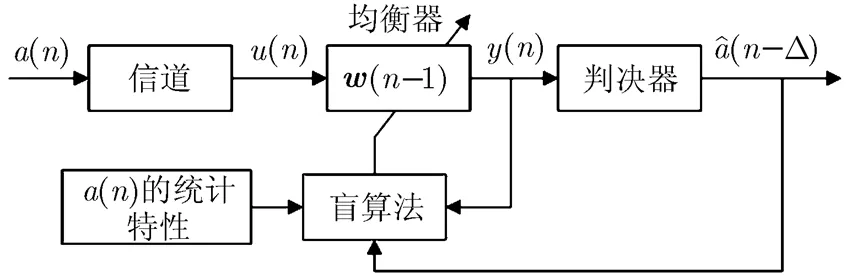
图1 基带通信系统原理图
2.1 常模算法(CMA)
CMA算法是Godard算法的一个特例。其代价函数为
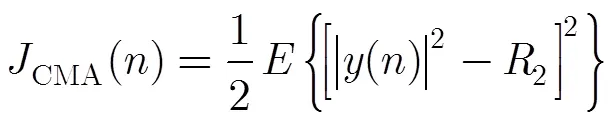
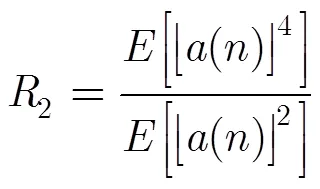
常模算法剩余误差计算为
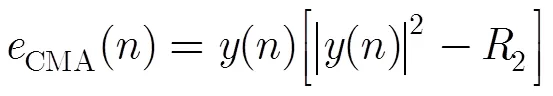
利用最速下降法,可以得出均衡器权值系数的迭代更新公式为
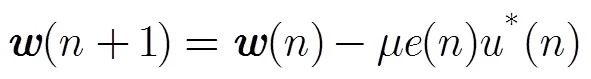
2.2 判决引导最小均方误差(DD-LMS)算法
DD-LMS算法的中心思想为:在盲均衡算法处理的过程中,当误码率足够小时,LMS算法中的期望信号可由盲均衡算法所得的估计值进行代替,即由判决器的输出代替。
利用判决器对盲均衡的输出进行判决。
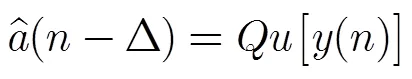
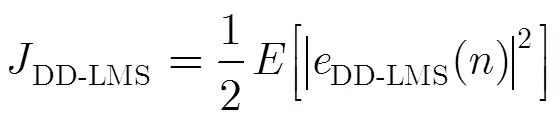
误差计算表达式为
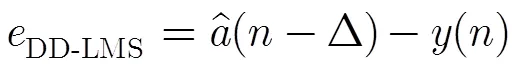
DD-LMS算法虽然收敛后剩余误差较小,但是当信道眼图未完全打开或者有外在干扰时错判的几率很大,导致无法收敛,因此,在双模切换盲均衡算法中必须要等待盲均衡算法完全收敛、眼图完全打开才有更好的效果。
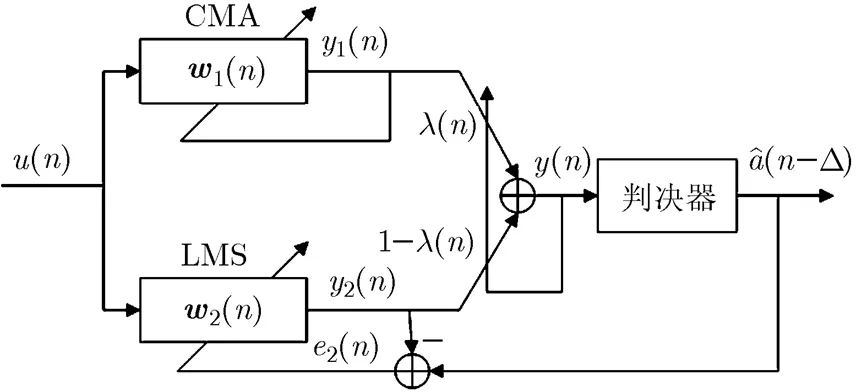
图2 CMA与DD-LMS算法组合原理图
3 基于凸组合结构的自适应双模切换盲均衡算法
改进所得的算法原理如图2所示,将CMA算法与DD-LMS进行凸组合,构成一种自适应切换的双模盲均衡结构。由于传统CMA算法的代价函数中仅包含输入信号的幅度信息,因此为了克服其对相位不敏感的不足,需要对CMA算法和DD-LMS算法进行修正。整个系统的输出为
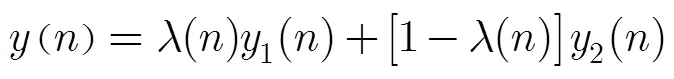
3.1 修正CMA算法
凸组合结构中修正CMA滤波器的代价函数为
权值迭代更新公式为
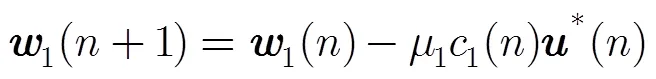
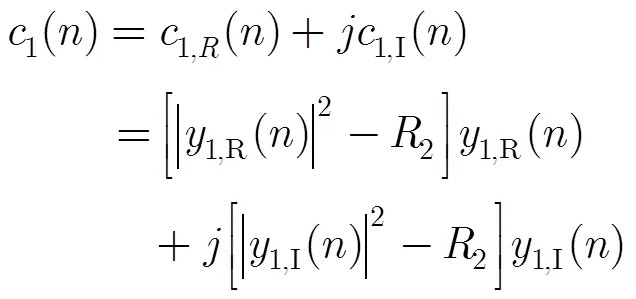
3.2 修正DD-LMS模式
在修正DD-LMS模式算法中,其代价函数为近似均方判决误差。
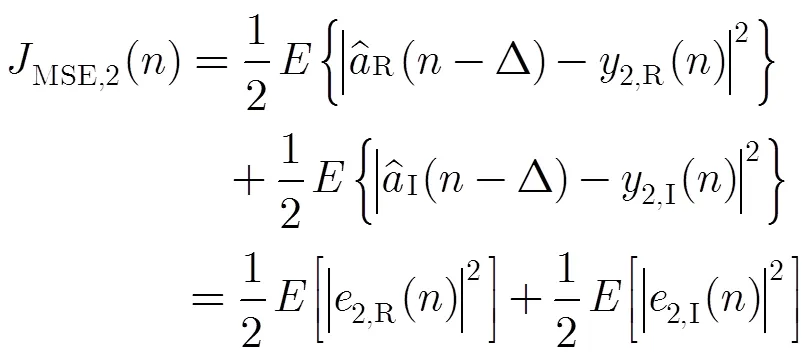
迭代更新公式为
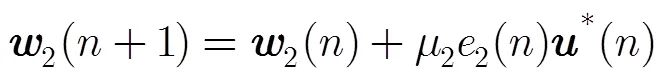
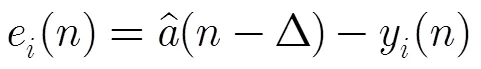
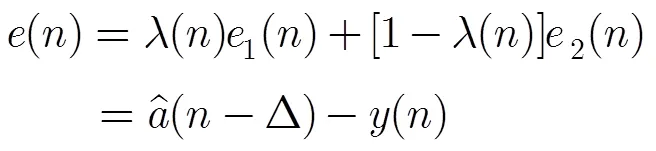
3.3联合参数的构造
为了使盲均衡器充分收敛,设定联合参数以最小化CMA均衡器的代价函数为准则,因此定义整个系统的代价函数为
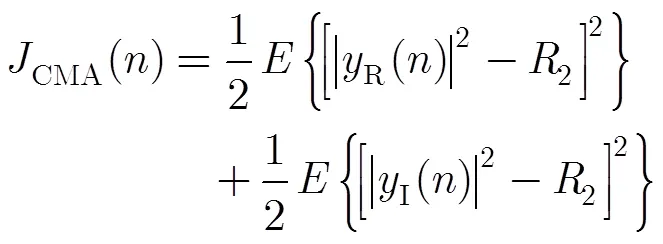
该代价函数同时利用星座图的幅度信息和相位信息,能够有效避免由于信道而发生的相位偏移,更好地恢复传输信号。
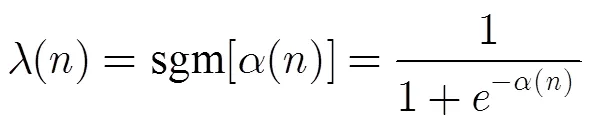
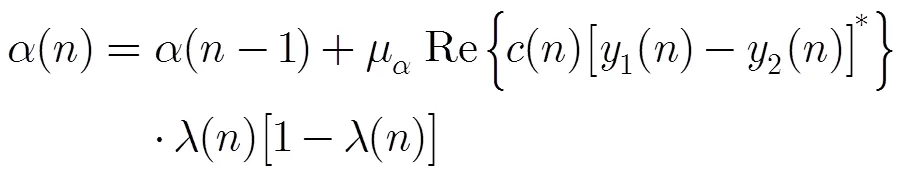
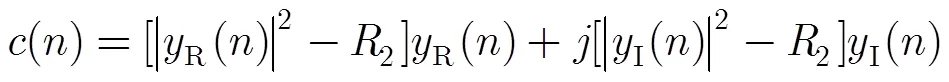
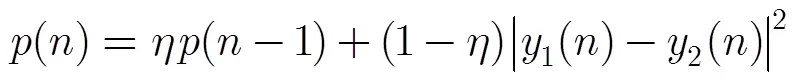
则混合参数的迭代式(18)变为
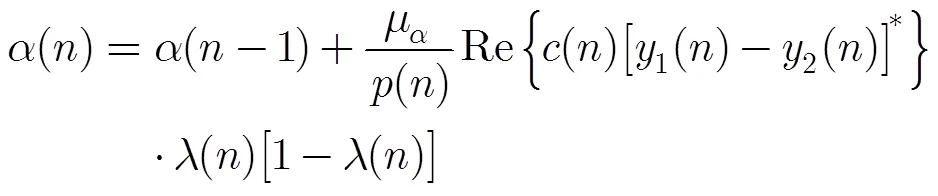
4 稳态性能分析
本节,在稳态条件下对修正CMA与LMS算法组合的系统推导其稳态均方误差的理论模型。从文献[9,10]中可知系统整体输出的超量均方误差(Excess Mean Squared Error, EMSE)不仅与所组成单个滤波器的EMSE相关,还与其交叉EMSE相关。
为方便描述,预先定义所组成滤波器的EMSE和它们的交叉稳态EMSE为
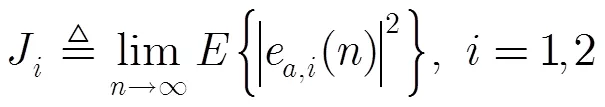
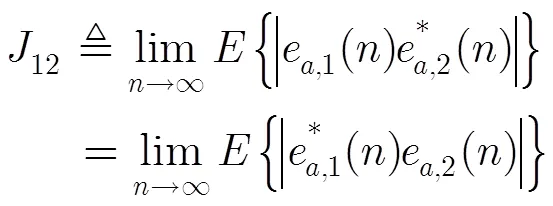
组合结构的等效先验误差为
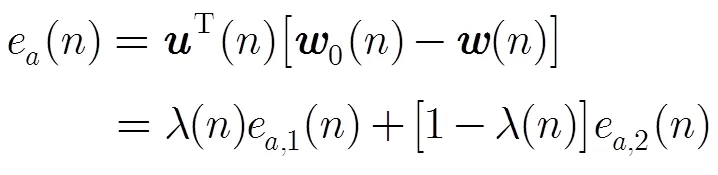
整体系统的等效稳态EMSE可以定义为
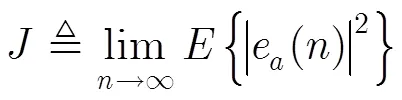
由式(22)~式(25)可得整个系统稳态EMSE估计值计算式为
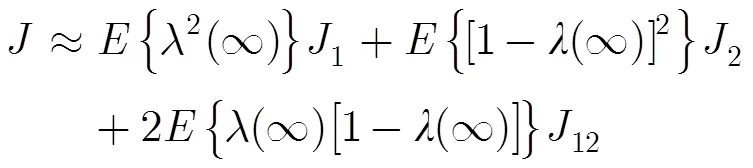
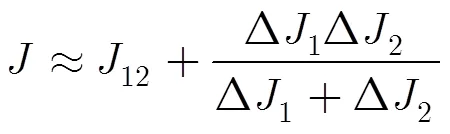
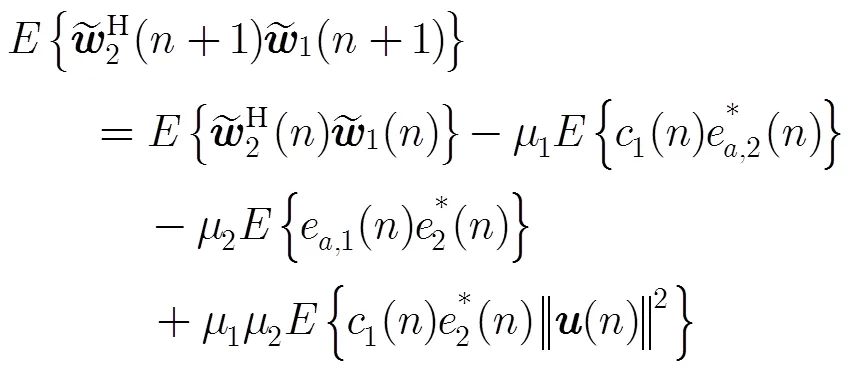
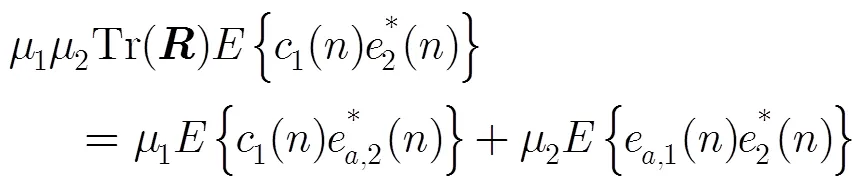
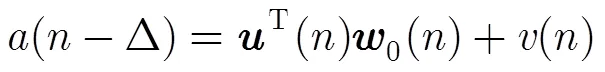
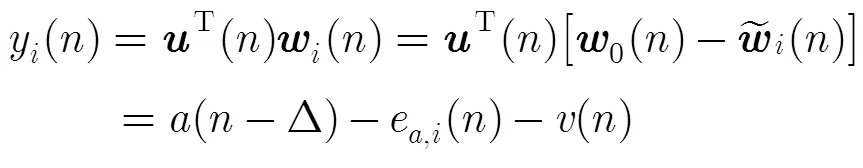
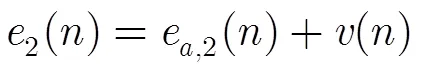
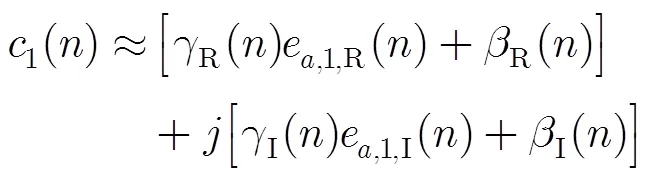
其中
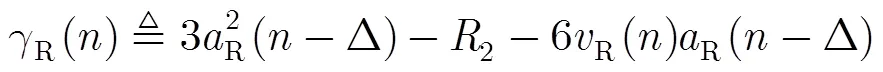
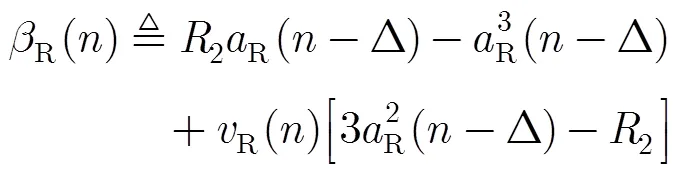
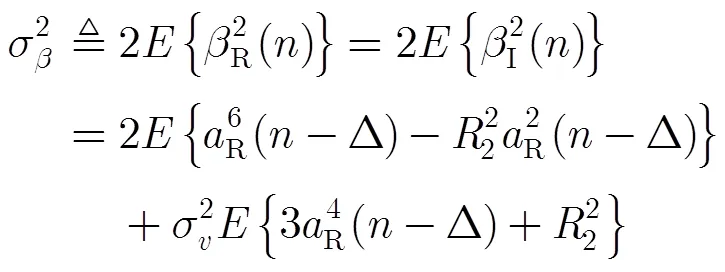
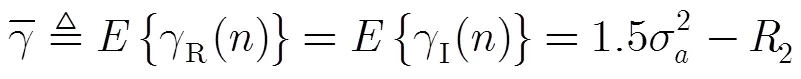
利用式(30),式(32)和式(33)以及文献[14]中的结论可以得到如下的近似关系:
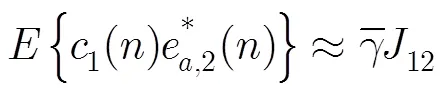
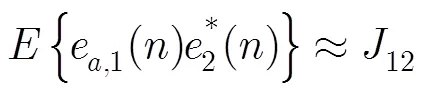
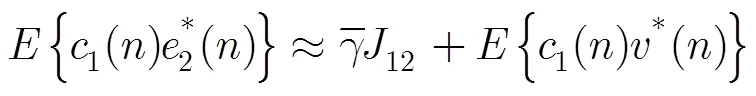
又
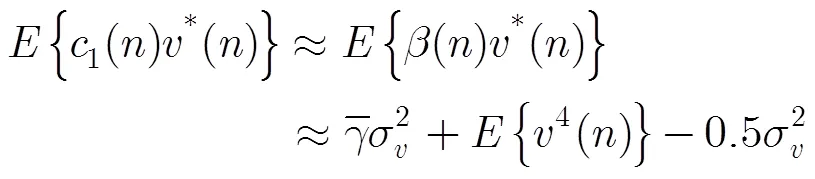
将式(38),式(39)和式(41)代入式(29),又由于,,则可得
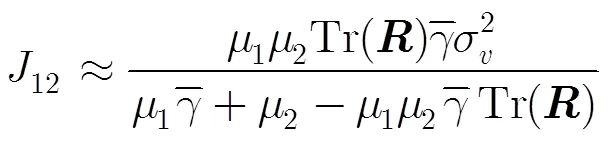
至此,已经推导出组合滤波器的交叉稳态EMSE的理论模型。参考文献[14],其推导出的CMA和LMS滤波器的稳态EMSE如式(43)和式(44):
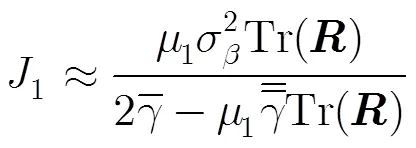
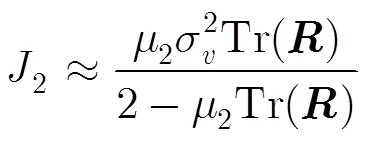
5 仿真试验
5.1 混合参数归一化处理的仿真验证
为了验证归一化处理后所得式(21)的性能,通过仿真进行验证。试验过程中,在迭代至10000点时使信道脉冲响应发生突变,式(18)中。其他条件与5.2节中相同。分别使用式(18)和式(21)所得的EMSE(dB)曲线和联合参数取值变化如图3所示。
从图3中可以看出,两式的使用均能使组合均衡器良好地工作,且能够发现,在初始阶段通过使联合参数的值趋近于1来使系统的输出更依赖于CMA均衡器从而实现粗均衡,在眼图打开后使趋近于0来依赖DD-LMS模式以进一步降低剩余误差。
通过比较分析图3(c)可以发现,使用式(18)得到的联合参数值变化是连续的并且较为缓慢,而使用式(21)得到的联合参数值初始阶段在0和1之间快速振荡,且在双模式切换时也比较果断快速,因此该式的选择对参数的变化更加敏感,从图3(a)和图3(b)的比较中也能够发现使用式(21)拥有更快的收敛速率。
5.2 与相关算法的仿真对比
仿真试验条件如下:发射信号的调制方式为256-QAM,输入信噪比为30 dB,通信信道为典型的话音传输信道[15],存在相位偏移,其脉冲响应为[-0.005-0.0040.009+0.03-0.024-0.1040.854+0.520-0.218+0.2730.049+0.074-0.016+0.020],所采用复数均衡器的阶数为21,中心抽头系数的初始化值为,其余抽头系数初始值为。仿真中所得学习曲线均是200次Monte-Carlo试验所得到的平均结果。另外,通过使信道脉冲响应突变来验证算法的跟踪性能,该脉冲响应值为[0.3 1 0.3]。参数取值为:均衡器阶数为21,,,式(21)中,判决门限值为0.2,遗忘因子的取值对算法性能的影响非关键因素,因此取值遵循合理的原则设定为0.9。
为了验证算法的性能,将本文提出的算法与文献[7]和文献[8]中的算法进行仿真比较。试验过程中,在迭代至20000点时使信道脉冲响应发生突变。文献[7]和文献[8]算法的参数取值与其文献中原有取值相同。则比较3种算法的EMSE曲线如图4所示。各算法均衡前后星座图对比如图5所示。
从图4中可以看出,在仿真条件相同的情况下,各个算法均随着迭代的进行逐渐收敛,但是本文算法在迭代至1700点时即收敛,而文献[7]和文献[8]算法的收敛点数分别为2200和12000,同时,本文算法均方误差也更低。从图5星座图收敛情况来看,本文算法收敛的效果也优于文献[7]和文献[8]。由此可以表明本文所提出的双模切换盲均衡算法拥有更优的收敛和稳态特性,在不影响整体性能的前提下实现了CMA与DD-LMS算法之间的自适应切换。
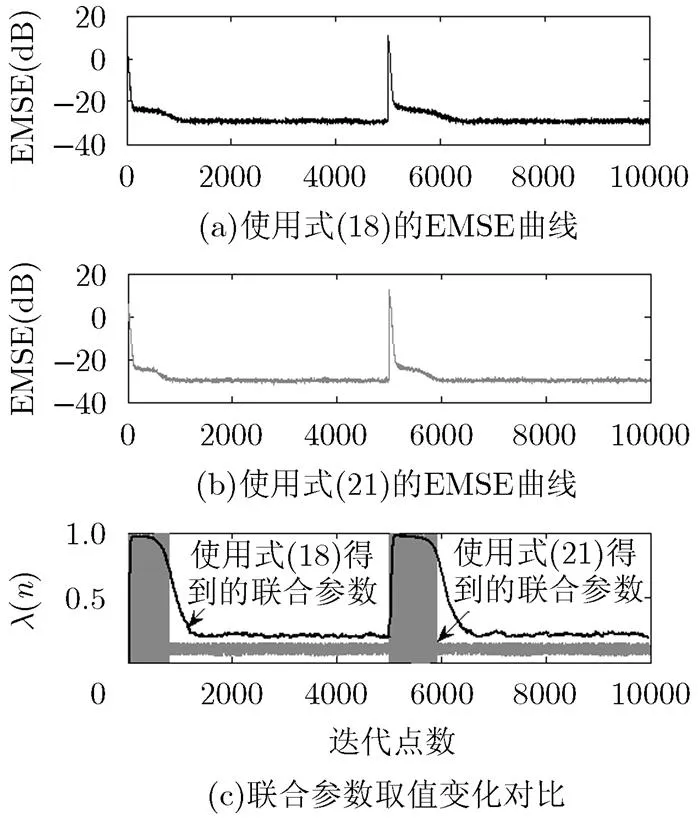
图3 EMSE曲线图及联合参数变化图
5.3 不同信噪比条件下的仿真
让本文算法在输入信噪比分别为10 dB, 20 dB, 30 dB的条件下仿真,来验证算法在不同信噪比条件下的均衡性能。仿真其它条件与5.2节中相同。
图6为其它条件不变,仅改变信噪比所得到的对比图。从图中可以看出,本文算法在不同信噪比条件下收敛后的稳态误差不同,但均具有很快的收敛速率且效果表现比较稳定,足以说明本文算法在不同信噪比,尤其是低信噪比条件下也能很好地收敛。
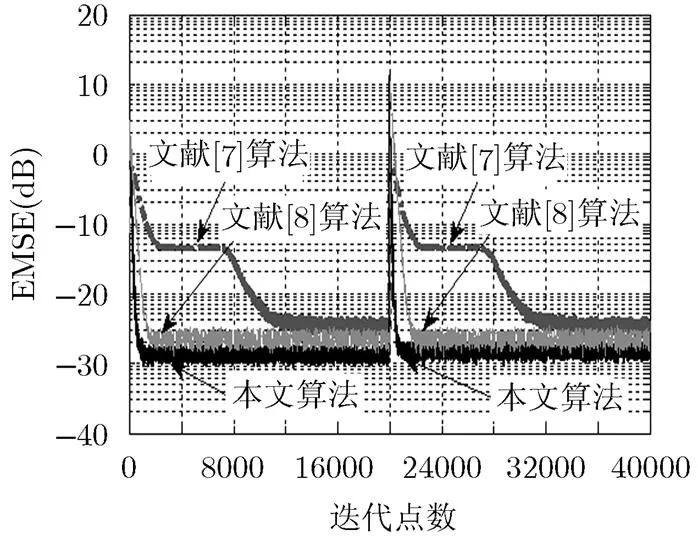
图4 3种算法EMSE曲线对比
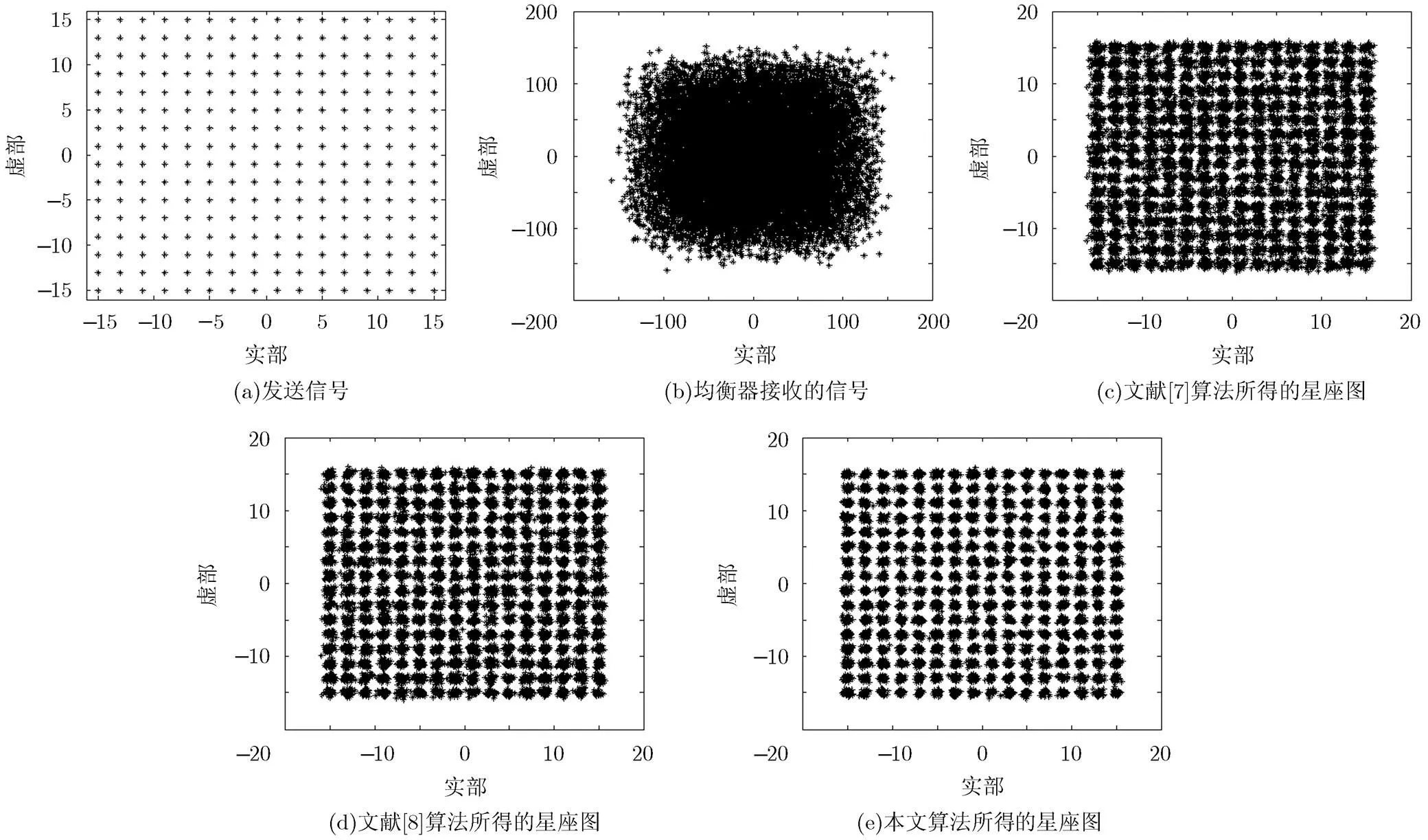
图5 3种算法收敛后的星座图对比
6 实际传输过程均衡性能测试
在此节使用一段实际采集的某军用标准短波通信信号进行盲信道均衡测试。该信号的时域波形为:信号的调制方式为16-QAM,符号率为2400波特。传输信号的时域和时频图显示如图7所示。
从图7中可以看出,所采用的实际传输信号表现出很强的衰落特性,在不同时间不同频率随机出现衰落。为了减小同步误差的影响,采用了频率十分精确的本地载波,利用锁相环跟踪载波相位以及采用最大平均功率点定时同步方法。处理输出星座图如图8所示。
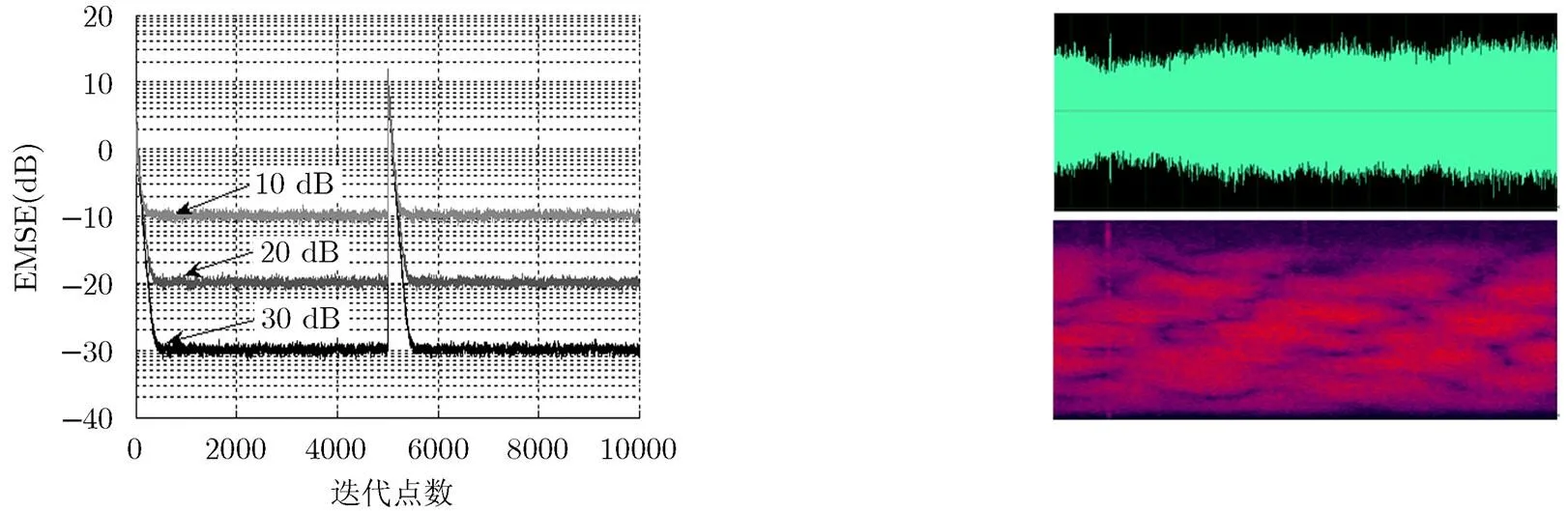
图6 不同信噪比条件下EMSE对比图 图7 传输信号的时域和时频图显示
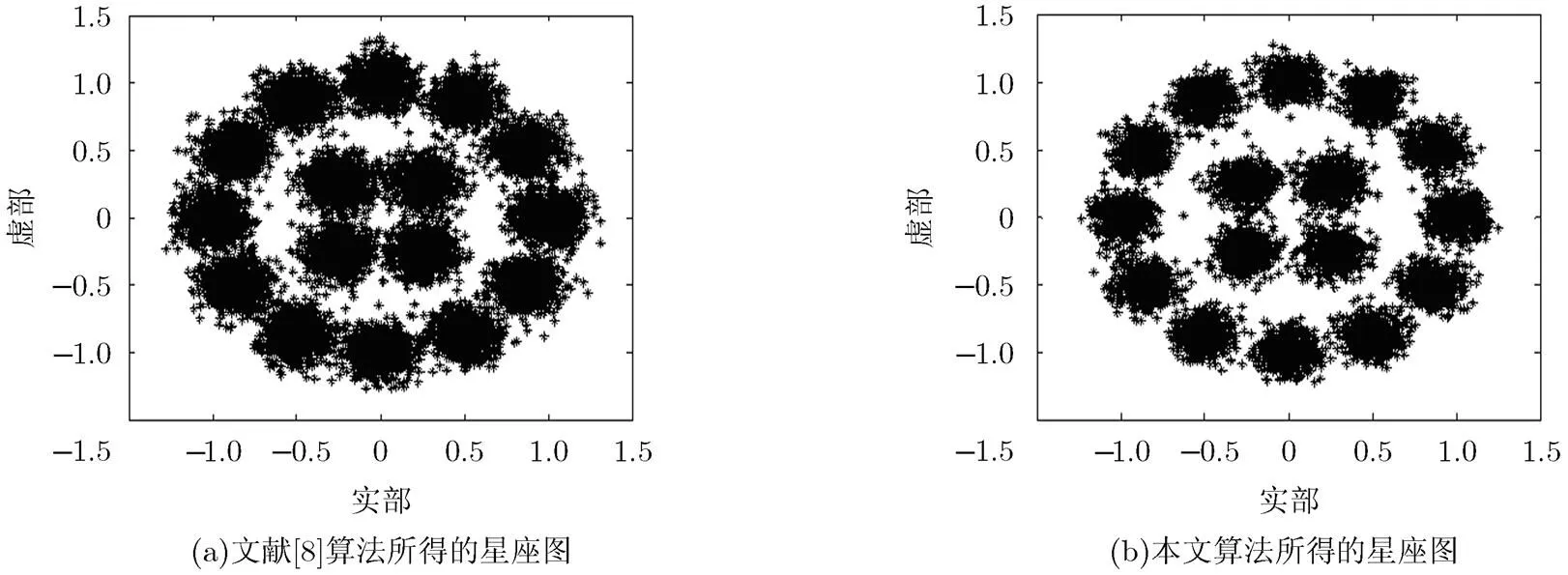
图8 实际信号传输条件下的星座图
从图8的星座图对比中可以看出,本文算法在实际传输信号的测试中具有较好的性能,且其均衡性能优于文献[8]所提算法。
7 结论
本文提出一种新的双模切换盲均衡算法。该算法通过对CMA算法和DD-LMS算法进行凸组合,并借助新引进的符合一定规则迭代变化的联合参数实现两种模式之间的自动切换;另一方面通过对原始盲均衡算法修正和混合参数归一化的利用避免了恢复信号的相位偏移并加快了收敛速率。理论分析和仿真验证的结果表明本文的改进具有可行性,稳态分析具有正确性,并通过与其它同类算法的比较验证了其更优的收敛速率和稳态性能。本文所提出的算法还可以结合其它改进以实现在不同条件下的更优的性能。
[1] RAGHEB A M, SHOAIB M, ALSHEBEILI S,. Enhanced blind equalization for optical DP-QAM in finite precision hardware[J]., 2015, 27(2): 181-184.
[2] JIA Z, CAI Y, CHEN H C,. Performance comparison of spectrum-narrowing equalizations with maximum likelihood sequence estimation and soft-decision output[J]., 2014, 22(5): 6047-6059.
[3] SHAH S M, SAMAR R, NAQVI S M R,. Fractional order constant modulus blind algorithms with application to channel equalisation[J]., 2014, 50(23): 1702-1704.
[4] XIAO Y and YIN F. Blind equalization based on direction gradient algorithm under impulse noise environment[J]., 2014, 13: 171-177.
[5] 饶伟. 多径衰落环境中具有调制识别能力的盲均衡新算法[J]. 电子学报, 2013, 41(7): 1284-1289. doi: 10.3969./j.issn.0372- 2112.2013.07.007.
RAO W.New blind equalization algorithm with ability of modulation classification under the condition of multipath propagation[J]., 2013, 41(7): 1284-1289. doi: 10.3969./j.issn.0372-2112.2013.07.007.
[6] 王成, 杨宾, 王大磊. 基于星座修正聚类的双模式盲均衡算法[J]. 信号处理, 2012, 28(8): 1194-1199.
WANG C, YANG B, and WANG D. Dual-mode blind equalization algorithm based on clustering[J]., 2012, 28(8): 1194-1199.
[7] 赵良, 汪春梅, 孙洪波. 逐幸存序列算法引导的快速盲均衡算法[J]. 西安电子科技大学学报(自然科学版), 2013, 40(2): 201-206. doi: 10.3969/j.issn.1001-2400.2013.02.032.
ZHAO L, WANG C, and SUN H. Fast blind equalization algorithm based on PSP[J]., 2013, 40(2): 201-206. doi: 10.3969/j.issn.1001-2400.2013. 02.032.
[8] 阮秀凯, 蒋啸, 李昌. 一种适用于高阶 QAM 系统 Bussgang 类盲均衡新方法[J]. 电子与信息学报, 2012, 34(8): 2018-2022. doi: 10.3724/SP.J.1146.2011.01403.
RUAN X, JIANG X, and LI C. A novel method of bussgang-type blind equalization in high-order QAM systems[J].&, 2012, 34(8): 2018-2022. doi: 10.3724/SP.J.1146.2011.01403.
[9] 洪丹枫, 苗俊, 苏健, 等. 一种变步长凸组合LMS自适应滤波算法改进及分析[J]. 电子学报, 2014, 42(11): 2225-2230. doi: 10.3969 /j.issn.0372-2112.2014.11.015.
HONG D, MIAO J, SU J,. An improved variable step-size convex combination of LMS adaptive filtering algorithm and its analysis[J]., 2014, 42(11): 2225-2230. doi: 10.3969/j.issn.0372-2112.2014.11. 015.
[10] ARENAS-GARCIA J, FIGUEIRAS-VIDAL A R, and SAYED A H. Mean-square performance of a convex combination of two adaptive filters[J]., 2006, 54(3): 1078-1090.
[11] FAN L, JUNWEN Z, JIANJUN Y,. Blind equalization for dual-polarization two-subcarrier coherent QPSK-OFDM signals[J]., 2014, 39(2): 201-204.
[12] LUO C, LI G, YANG X,. New convex combination strategy for the MMSE blind equalization algorithms[J].&, 2009, 23(1): 37-41.
[13] AZPICUETA-RUIZ L A, FIGUEIRAS-VIDAL A R, and ARENAS-GARCIA J. A normalized adaptation scheme for the convex combination of two adaptive filters[C]. International Conference on Acoustics, Speech, and Signal Processing, Las Vegas, 2008: 3301-3304.
[14] FILHO J M, MIRANDA M D, and SILVA M T M. A regional multimodulus algorithm for blind equalization of QAM signals: introduction and steady-state analysis[J]., 2012, 92(11): 2643-2656.
[15] PICCHI G and PRATI G. Blind equalization and carrier recovery using a “stop-and-go” decision-directed algorithm[J]., 1987, 35(9): 877-887.
Dual Mode Blind Equalization Algorithm Based on Adaptive Switching
ZENG Leya①XU Hua①WANG Tianrui②
①(,,’710077,)②(,,210046,)
The constant modulus algorithm is widely used in the blind equalization of wireless communication system, in order to reduce further the steady-state error, it is usually combined with the decision directed least mean square algorithm. The traditional dual mode blind equalization algorithm can achieve the hard switching of the two algorithms by setting the threshold value artificially. The rationality of the switch can not be guaranteed, it also can not fully highlight the advantages of dual mode switching. In this paper, the structure of the convex combination is used to achieve the switching between two modes and can adaptively choose the switching time. It improves the convergence rate and reduces the steady-state error by modifying the algorithm and normalizing the mixed parameter. In addition, the steady-state performance is derived and analyzed. Simulation results demonstrate that the performance of the model is consistent with the results, the effect of parameter normalization is obvious. Compared with other similar dual mode switching algorithms, it has better performance.
Signal processing; Blind equalization; Convex combination; Dual-mode; Normalization
TN911.7
A
1009-5896(2016)11-2780-07
10.11999/JEIT160099
2016-01-21;改回日期:2016-06-08;
2016-09-01
曾乐雅 zengleya@163.com
国家自然科学基金(61001111)
The National Natural Science Foundation of China (61001111)
曾乐雅: 男,1990年生,博士生,研究方向为通信信号处理、自适应滤波.
许 华: 男,1976年生,副教授,主要研究方向为通信信号处理、盲信号处理.
王天睿: 女,1992年生,硕士生,研究方向为信息采集与处理.

