单快拍数据的分布式阵列DOA估计

向 洪 王 俊 魏少明 高 越 毛士艺



单快拍数据的分布式阵列DOA估计

向 洪*①王 俊①魏少明①高 越②毛士艺①

①(北京航空航天大学电子信息工程学院 北京 100191)②(航天恒星科技有限公司 北京 100086)

该文针对分布式阵列相干信号单次快拍波达方向估计问题，提出一种基于状态空间平衡法的1维波达角估计算法。该算法首先直接利用单快拍数据以分布式阵列每个子阵单元进行Hankle矩阵构造，然后采用状态空间平衡法，分别获得低精度无模糊的子阵单元内DOA估计和高精度有模糊的子阵单元间DOA估计，最后结合配对和解模糊算法获得高精度无模糊DOA估计。该算法不受信号形式限制，可同时对相干信号和非相干信号进行处理，能充分利用分布式阵列扩展阵列物理孔径特性，获得较高的DOA估计精度。计算机仿真结果验证了所提算法的有效性。

DOA估计；分布式阵列；Hankle矩阵；解模糊

1 引言

波达方向(Direction Of Arrival, DOA)估计是当前阵列信号处理领域的研究热点，其原理是利用阵列传感器组接收到的回波信号估计信源位置和方位[1]。早期的DOA估计算法如常规波束形成法(Conventional Beam-Forming, CBF)[2]直接利用空域各阵元的接收数据替代传统时域处理中的时域数据，但是其无法突破瑞利限。为了突破瑞利限，基于空间谱估计技术的超分辨算法得到发展。其中的典型算法包括多重信号分类(MUltiple SIgnal Classification, MUSIC)[3,4]算法和旋转不变子空间(Estimation of Signal Parameters by Rotational Invariance Techniques, ESPRIT)[5,6]算法。MUSIC算法易于实现精度高且对任意阵列都能适用，但是其计算量巨大，需要进行谱峰搜索。ESPRIT算法则对阵列要求较高，需要两个子阵满足旋转不变性，但是其计算量相对较少。两者都需要利用多次快拍数据构造协方差矩阵，在处理相关或相干信号时，需要进行空间平滑[7]、矩阵重构[8]等解相干预处理，进而进行DOA估计。然而在实际信号环境中，多径效应和复杂的电磁干扰会产生大量的相关或相干信号，同时高速运动目标对系统的实时性要求高，接收到的有效数据仅有几次快拍数据，基于大量快拍数据的DOA估计算法在现有硬件系统情况下无法满足实际需要，为此利用单快拍数据进行DOA估计成为一种解决方案。文献[9]直接利用接收的快拍数据构造Hankle矩阵作为伪协方差矩阵，进而利用空间谱估计的方法进行DOA估计，但是该方法类似于MUSIC算法，仍然需要进行谱峰搜索，因此计算量较大。文献[10]则在文献[9]的基础上为了不损失阵列自由度，提出了采用Toeplitz矩阵作为伪协方差矩阵，但其矩阵重构机理需要入射信号类型是初始相位为零的非圆信号，在实际情况下，该约束条件几乎不可实现，因此很难推广应用[11]。而文献[12]则在文献[10]的基础上提出了一种基于加权求和的方式构造伪协方差矩阵，该算法可充分利用单快拍数据，更具一般性。

但是上述算法仅在单个阵列的基础上进行研究，而以分布式阵列作为平台的研究则相对较少。文献[13-15]提出了基于ESPRIT的双尺度分布式阵列DOA估计方法，首先通过子阵列获得无模糊精度较低的子阵单元内DOA估计，再利用阵列间的旋转不变性获得有模糊但精度高的子阵单元间DOA估计，最后通过解模糊获得无模糊精度高的DOA估计，但是在低信噪比条件下，算法的DOA估计性能将明显下降。文献[16]则提出了基于ESPRIT算法的多尺度的DOA估计方法，在不增加阵元数的情况下，可降低信噪比门限。但是这些方法都针对的是多快拍数据，且无法直接对相干信号源进行处理，因此本文提出了针对相干信号源的单快拍数据分布式阵列DOA估计方法。该方法首先利用接收的单快拍数据构造Hankle矩阵作为伪协方差矩阵，然后利用分布式阵列子阵单元内和子阵单元间的空间旋转不变性，采用状态空间平衡法分别获得无模糊精度低的子阵单元内DOA估计和有模糊精度高的子阵单元间DOA估计，最后通过配对和解模糊算法，采用逐次递推的方式，获得分布式阵列的DOA高精度估计。

2 分布式阵列回波建模

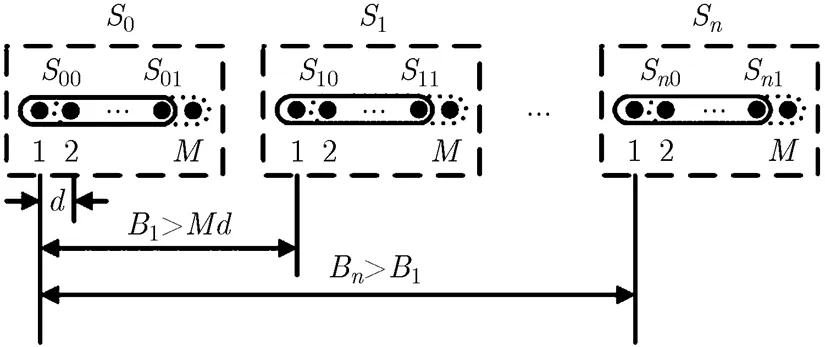
图1 分布式均匀线阵示意图

假设个远场窄带点源信号入射到分布式阵列上，为入射信号，为信号入射方向；噪声为零均值加性高斯白噪声，其方差为；不考虑通道不一致、互耦等因素影响，以基准单元阵第1个阵元作为参考阵元，可得到第个入射信号到第个阵元的延时为

对于远场窄带信号，有式(2)成立。

3 分布式阵列DOA估计方法

3.1 Hankle矩阵构造

3.2子阵单元内DOA估计

3.3 子阵单元间DOA估计

由于分布式阵列子阵间存在空域旋转不变性，可选择基准单元阵与子阵进行子阵单元间DOA估计，为了后续计算方便以及解模糊，本文利用分布式阵列子阵单元与之间存在的空域旋转不变性，将式(5)代入式(10)和式(11)中，类似于子阵单元内分解，虽然子阵阵元数减少1，但存在式(22)：

由于式(22)与式(14)具有相同的形式，因此可采用状态空间平衡法获取子阵单元间估计算子为

3.4配对和解模糊

由于式(28)中基于多基线的方法在解缠绕过程中，只利用了基准单元阵，而分布式子阵之间相互利用的信息较少。所以本文采用首先利用基准单元阵获得的精度低无模糊的子阵单元内DOA估计与最短基线子阵单元进行解模糊，获得精度较高无模糊的子阵单元间DOA估计；然后再利用上一步获得的精度较高无模糊的阵列间DOA估计值作为新的基准值与后续较长基线子阵进行解模糊，逐次递推，最终获得最长基线子阵的高精度无模糊DOA估计。

综上所述，本文提出的单快拍数据分布式阵列DOA估计算法步骤如下：

4 仿真及分析

为验证本文提出的单快拍数据的分布式阵列DOA估计方法，本文从如下3个方面进行算法仿真和分析。

仿真1 验证算法对相关信号的解相关能力 4个完全相干的远场窄带信号入射角分别为,,和。分布式阵列布阵方式按照图2所示阵列结构模型的多基线方式进行布阵。其中总阵元数为48，由3个子阵组成，每个单元子阵阵元数为16，阵元间距设置为，子阵单元0与子阵单元1间距设置为32，子阵单元0与子阵单元2间距设置为144，处理数据为单快拍数据。

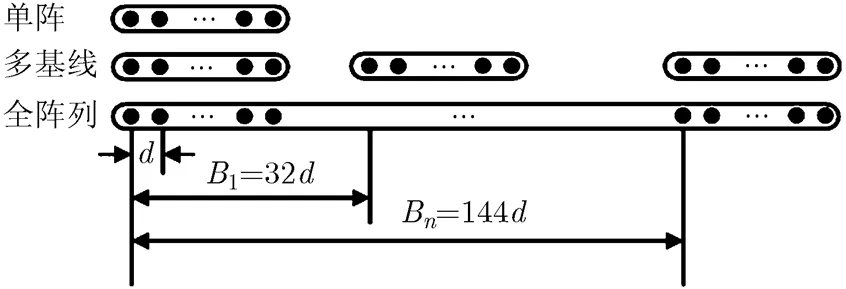
图2 阵列结构模型

在信噪比SNR=20 dB情况下进行10000次Monte-Carlo仿真实验。图3给出了分布式阵列估计值的分布柱状图，其中图3(a)为分布式阵列子阵内估计值分布柱状图，图3(b)为分布式阵列子阵单元间估计值分布柱状图。对比图3(a)和图3(b)，可看出多相干入射信号条件下，子阵单元内DOA估计值柱状分布图相对分散，以入射信号为例，其在10000次Monte-Carlo实验估计值在区间[]呈高斯分布，在真实值最高峰值不超过70次，方差较大；而子阵间DOA估计值柱状分布图则相对集中，其在10000次Monte-Carlo实验估计值在区间[]呈高斯分布，在真实值最高峰值接近400次，方差相对较小。显然，在多相关信号入射条件下，本文算法一方面较好地实现了子阵单元内DOA估计与子阵单元间DOA估计的解相关，都获得了较为准确的DOA估计值；另一方面相比于较低精度的子阵单元内DOA估计，获得了更高精度的子阵单元间DOA估计，说明本文算法较好地解决了子阵单元内DOA估计与子阵单元间DOA估计的配对和解模糊问题，同时由于分布式子阵单元间估计利用的阵列的物理孔径明显大于单个子阵单元的阵列物理孔径，因此子阵单元间DOA估计值精度明显高于子阵单元内DOA估计值。

仿真2 验证单快拍数据分布式阵列扩展孔径的有效性 2个远场窄带信号入射角分别为,。分布式阵列布阵方式选择图2阵列结构模型的多基线分布式阵列布阵方式；与单阵和相同孔径的全阵列进行对比。处理数据均为单快拍数据，其中SNR范围设置为，步长为2 dB，在每个SNR条件下进行1000次Monte-Carlo仿真试验。算法的均方根误差(Root-Mean-Square Error, RMSE)定义如下：

式中，为独立试验次数，为入射信号个数，为第个入射信号DOA的第次估计值，为第个入射信号的真实值。图4给出了单阵，多基线分布式阵列，以及全孔径阵列的RMSE随SNR的变化图。单阵-本文算法和全阵列-本文算法采用的算法为本文提出的子阵单元内DOA估计算法，直接利用单个子阵数据进行DOA估计；多基线-本文算法采用的算法为本文提出的分布式阵列DOA估计方法，利用子阵单元内DOA估计算法和子阵单元间DOA估计算法，经过配对和解模糊获得高精度DOA估计。同时将本文算法与文献[13,15]的单站-ESPRIT，多基线-ESPRIT，全阵列-ESPRIT算法(快拍次数为100次)分别从相干入射信号和非相干信号进行比较。从图4(a)可看出，在非相干信号入射条件下，本文算法和基于ESPRIT的多快拍算法均达到了较好的估计性能。在高信噪比(SNR>10 dB)下，本文算法相比于多基线-ESPRIT算法略有不足，其主要原因为本文算法仅适用地单快拍数据，而多基线-ESPRIT则使用了100次快拍数据；但是在低信噪比(SNR<10 dB)条件下，本文算法的性能优于多基线-ESPRIT算法，其主要原因为本文算法对子阵单元内矩阵变换和子阵单元间矩阵变换采用了相同的矩阵变换方法，在低信噪比仍然能较好地实现子阵单元内DOA估计与子阵单元间DOA估计的配对，而多基线-ESPRIT算法则是利用特征值对应的特征向量包含信源信息，同一信源对应的列向量内积为1，不同为0，其在低信噪比条件下获得的配对矩阵是不准确的。从图4(a)中，可发现多基线-ESPRIT性能比全阵列-ESPRIT性能好，是因为该算法在平移量为一个半波长时，性能并不能达到最优，不能逼近均匀阵理论值，而多基线-ESPRIT的精估计则可很好地逼近理论值[22]。从图4(b)可看出，本文的算法仍能较好地实现较高精度DOA估计性能，但是基于ESPRIT的多快拍数据算法则失效，必须经过解相关算法，才能进行下一步处理。对比图4(a)和图4(b)，可发现信号的相关性会影响本文算法的性能，对于相干信号，本文算法需要在较高的信噪比条件下，才能得到较为精确的DOA估计值；对于非相干信号，本文算法可在较低信噪比条件下，实现精确的DOA估计。

仿真3仿真基线间距和信噪比对多基线分布式阵列估计精度的影响 多基线分布式阵列首先利用两个子阵单元间的较短基线距离，获得了在低信噪比条件下较高DOA估计值，然后利用其对长基线分布式阵列估计值进行解模糊，最终获得了在低信噪比条件下的高精度估计性能。布阵方式分别选择图2阵列结构模型的多基线分布式阵列，单元子阵阵元数为16; 2个远场窄带信号入射角分别为,；子阵单元0与子阵单元1间距设置为32，子阵单元0与子阵单元2间距设置为变化，步长为16，其中；非相干信号入射时，SNR分别设置为3 dB, 6 dB和9 dB；相干信号入射时，SNR分别设置为12 dB, 15 dB和18 dB。从图5可看出，在相同的信噪比条件下，多基线分布式阵列的RMSE随着基线距离的增大存在基线距离门限效应，在小于基线距离门限条件下，其RMSE随着基线距离增大而变小，在大于基线距离门限条件下，其RMSE随着基线距离增大而变大；当信噪比不同，分布式阵列的基线门限也不同，信噪比越低，基线距离门限越小，信噪比越高，基线距离门限越大。同时对比图5(a)和图5(b)，当入射信号为相干信号源时，分布式阵列需要更高的信噪比才能获得与非相干信号源相同的DOA估计性能。

5 结论

针对分布式阵列相干信号单次快拍波达方向估计问题，本文基于状态空间平衡法的1维波达角估计算法实现了分布式阵列DOA估计。通过对仿真分析可知，相比于传统的单阵列DOA估计，本文算法通过对多个单元子阵进行分布式优化布阵，实现了阵列物理孔径扩展，可在较低信噪比条件基本达到一个大孔径天线的相当的DOA估计性能，特别适用于一些雷达为了战场机动性以及当前硬件水平限制，无法直接制造大孔径雷达的情况；同时本文算法不受信号形式限制，可同时对相干信号和非相干信号进行处理。因此本文算法对于解决单快拍数据分布式阵列DOA估计方法提供了一种较好的解决方案。

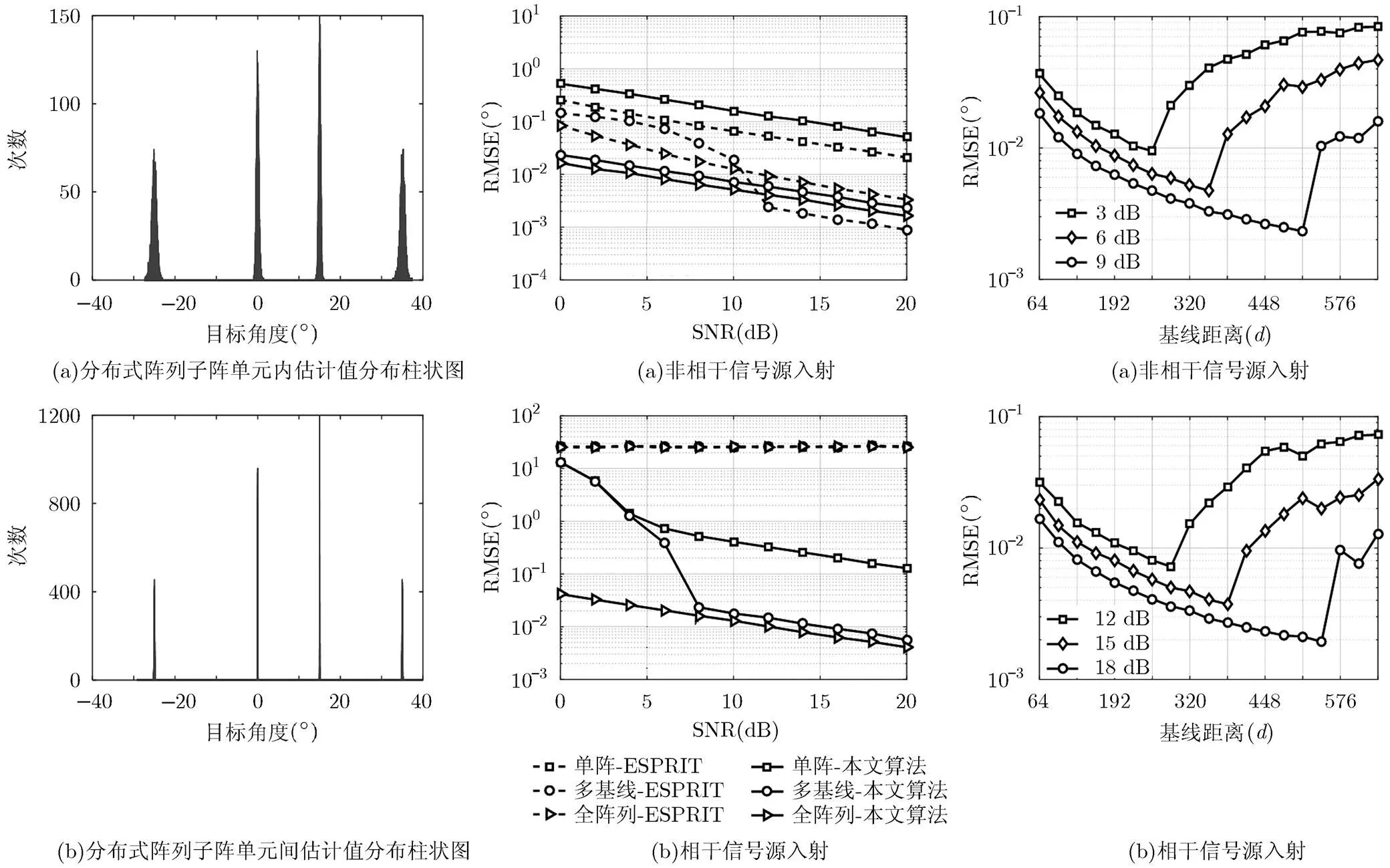
图3 分布式阵列估计值       图4 分布式阵列DOA估计       图5分布式阵列

分布柱状图随变化          随基线距离变化

[1] SCHMIDT R O. Multiple emitter location and signal parameter estimation[J]., 1986, 34(3): 276-280. doi: 10.1109/TAP. 1986.1143830.

[2] KRIM H and VIBERG M. Two decades of array signal processing research: the parametric approach[J]., 1996, 13(4): 67-94. doi: 10.1109/79.526899.

[3] 王伟, 王晓萌, 李欣, 等. 基于MUSIC算法的L型阵列MIMO雷达降维DOA估计[J]. 电子与信息学报, 2014, 36(8): 1954-1959. doi: 10.3724/SP.J.1146.2013.01281.

WANG Wei, WANG Xiaomeng, LI Xin,. Reduced- dimensional DOA estimation based on MUSIC algorithm in MIMO radar with L-shaped array[J].&, 2014, 36(8): 1954-1959. doi: 10.3724/SP.J.1146.2013.01281.

[4] ROY R and KAILATH T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J].,,, 1989, 37(7): 984-995. doi: 10.1109/29.32276.

[5] 梁浩, 崔琛, 代林, 等. 基于ESPRIT算法的L型阵列MIMO雷达降维DOA估计[J]. 电子与信息学报, 2015, 37(8): 1828-1835. doi: 10.11999/JEIT141295.

LIANG Hao, CUI Chen, DAI Lin,. Reduced-dimensional DOA estimation based on ESPRIT algorithm in MIMO radar with L-shaped array[J].&, 2015, 37(8): 1828-1835. doi: 10.11999/JEIT141295.

[6] SHAN T J, WAX M, and KAILATH T. On spatial smoothing for direction-of-arrival estimation of coherent signals[J].,,, 1985, 33(4): 806-811. doi: 10.1109/TASSP.1985.1164649.

[7] CHEN Y M, LEE J H, YEH C C,. Bearing estimation without calibration for randomly perturbed arrays[J]., 1991, 39(1): 194-197. doi: 10.1109/78.80780.

[8] KIM J T, MOON S H, HAN D S,. Fast DOA estimation algorithm using pseudocovariance matrix[J]., 2005, 53(4): 1346-1351. doi: 10.1109/TAP.2005.844459.

[9] 谢鑫, 李国林, 刘华文. 采用单次快拍数据实现相干信号DOA估计[J]. 电子与信息学报, 2010, 32(3): 604-608. doi: 10.3724/SP.J.1146.2009.00321.

XIE Xin, LI Guolin, and LIU Huawen. DOA estimation of coherent signals using one snapshot[J].&, 2010, 32(3): 604-608. doi: 10.3724/SP.J.1146.2009.00321.

[10] 蒋柏峰, 吕晓德, 向茂生. 一种基于阵列接收信号重排的单快拍DOA估计方法[J]. 电子与信息学报, 2014, 36(6): 1334-1339. doi: 10.3724/SP.J.1146.2013.01242.

JIANG Baifeng, LU Xiaode, and XIANG Maosheng. Single snapshot DOA estimation method based on rearrangement of array receiving signal[J].&, 2014, 36(6): 1334-1339. doi: 10. 3724/SP.J.1146.2013.01242.

[11] WONG K T and ZOLTOWSKI M D. Direction-finding with sparse rectangular dual-size spatial invariance array[J]., 1998, 34(4): 1320-1336. doi: 10.1109/7.722717.

[12] 毛维平, 李国林, 谢鑫. 单快拍数据预处理的相干信号波达方向估计[J]. 上海交通大学学报, 2014, 48(10): 1362-1367.

MAO Weiping, LI Guolin, and XIE Xin. DOA estimation of coherent signals with preprocessed single snapshot[J]., 2014, 48(10): 1362-1367.

[13] LEMMA A N, VEEN A J, and DEPRETTERE E F. Multiresolution ESPRIT algorithm[J]., 1999, 47(6): 1722-1726. doi: 10.1109/78. 765149.

[14] 陈根华, 陈伯孝, 杨明磊. 分布式相参阵列及其二维高精度方向估计[J]. 电子与信息学报, 2012, 34(11): 2621-2627. doi: 10.3724/SP.J.1146.2012.00043.

CHEN Genhua, CHEN Baixiao, and YANG Minglei. High accuracy 2-D estimation using distributed coherent arrays[J].&, 2012, 34(11): 2621-2627. doi: 10.3724/SP.J.1146.2012.00043.

[15] 马严, 陈伯孝, 杨明磊, 等. 基于ESPRIT的多基线分布式阵列DOA估计方法[J]. 系统工程与电子技术, 2014, 36(8): 1453-1459. doi: 10.3969/j.issn.1001-506X.2014.08.01.

MA Yan, CHEN Baixiao, YANG Minglei,. Multi-baseline distributed array DOA estimation using ESPRIT algorithm[J]., 2014, 36(8): 1453-1459. doi: 10.3969/j.issn.1001-506X.2014. 08.01.

[16] 高世伟, 保铮. 利用数据矩阵分解实现对空间相关信号源的超分辨处理[J]. 通信学报, 1988, 9(1): 4-13.

GAO Shiwei and BAO Zheng. A family of data-based matrix decomposition for high-resolution array processing of coherent signals[J]., 1988, 9(1): 4-13.

[17] DAVID J H. State-space approaches to ultra-wideband Doppler processing[D]. [Ph.D. dissertation], Worcester Ploytechnic Institute, 2007.

[18] WANG J, WEI S M, SUN J P,. A GTD model and state space approach based method for extracting the UWB scattering center of moving target[J].(), 2011, 54(1): 182-196. doi: 10.1007/s11432-010-4137-z.

[19] AKAIKE H. A new look at the statistical model identification[J]., 1974, 19(6): 716-723. doi: 10.1109/TAC.1974.1100705.

[20] RISSANEN J. Modeling by shortest data description[J]., 1978, 14(5): 465-471. doi: 10.1016/0005-1098(78) 90005-5.

[21] WONG K T and ZOLTOWSKI M D. Self-initiating MUSIC-based direction finding and polarization estimation in spatio-polarizational beamspace[J]., 2000, 48(8): 1235-1245. doi: 10.1109/8.884492.

[22] MA Y, CHEN B, YANG M,. A novel ESPRIT-based algorithm for DOA estimation with distributed subarray antenna[J].,,, 2015, 34(9): 2951-2972. doi: 10.1007/s00034-015-9987-6.

DOA Estimation of Distributed Array with Single Snapshot

XIANG Hong①WANG Jun①WEI Shaoming①GAO Yue②MAO Shiyi①

①(,,100191,)②(,,100086,)

An algorithm of Directions Of Arrival (DOA) estimation based on the state-space method is proposed to deal with the problem of estimating DOA of multiple source signals from a single observation vector of distributed array. Hankle matrixes are firstly constructed by using the single snapshot of every subarray element. Then low accuracy and unambiguous DOA estimations are obtained by the single subarray, while high accuracy and ambiguous DOA estimations are obtained by the distributed array. Finally, high accuracy and unambiguous DOA estimations are obtained by using automatic pairing decorrelating. This algorithm has no relations with the correlation signals and can fully take advantage of the large aperture to acquire high DOA estimation. Computer simulation results confirm the effectiveness of the proposed algorithm.

DOA estimation; Distributed array; Hankle matrix; Decorrelating

TN911.23

A

1009-5896(2016)11-2767-07

10.11999/JEIT160093

2016-01-19；改回日期：2016-06-08；

2016-09-01

向洪 xianghong926@gmail.com

国家自然科学基金(61471019, 61501011, 61501012)，中央高校基本科研业务费专项资金(YWF-15-GJSYS-0068)，重点实验室基金(9140C800101140C80331)

The National Natural Science Foundation of China (61471019, 61501011, 61501012), The Fundamental Research Funds for the Central Universities (YWF-15-GJSYS-0068), The Key Laboratory Foundation (9140C800101140C80331)

向 洪： 男，1988年生，博士生，研究方向为阵列信号处理、分布式雷达等.

王 俊： 男，1972年生，教授，博士生导师，研究方向为雷达信号处理、实时信号处理等.

魏少明： 男，1985年生，博士，研究方向为超宽带目标散射参数高精度提取、数据关联、目标三维重构等.

高 越： 男，1987年生，硕士，工程师，研究方向为模式识别、卫星任务规划、地面站接收方向等.

毛士艺： 男，1935年生，教授，博士生导师，研究方向为目标跟踪、信息融合、高分辨率雷达信号处理等.