基于K-均值聚类和传统递归最小二乘法的高光谱图像无损压缩
高 放 孙长建 邵庆龙 郭树旭
基于K-均值聚类和传统递归最小二乘法的高光谱图像无损压缩
高 放 孙长建 邵庆龙 郭树旭*
(吉林大学电子科学与工程学院 长春 130012)
针对基于预测的高光谱图像无损压缩算法压缩比低的问题,该文将聚类算法与高光谱图像预测压缩算法相结合,提出一种基于K-均值聚类和传统递归最小二乘法的高光谱图像无损压缩算法。首先,对高光谱图像按光谱矢量进行K-均值聚类以提升同类光谱矢量间的相似度。然后,对每一聚类群分别使用传统递归最小二乘法进行预测,消除高光谱图像的空间冗余和谱间冗余。最后,对预测误差图像进行算术编码,完成高光谱图像压缩过程。对AVIRIS 2006高光谱数据进行仿真实验,所提算法对16位校正图像、16位未校正图像和12位未校正图像分别取得了4.63倍,2.82倍和4.77倍的压缩比,优于同类型已报道的各种算法。
高光谱图像;图像压缩;递归最小二乘法;聚类
1 引言
高光谱图像由于在地物的分类和识别上所特有的极强能力,在大气检测、资源管理、环境监测、军事侦查和矿产勘探等领域有着广泛的应用。近年来,伴随着光谱成像技术的飞速发展,高光谱图像越来越高的空间分辨率、谱间分辨率和时间分辨率导致其数据量的迅速上升,对高光谱图像的存储与传输造成了巨大的压力。高光谱图像作为最有价值的遥感观测数据之一,多用来对地物进行精确分类,在压缩时引起的任何图像数据的失真都是不可接受的,所以,即使有损压缩可以得到更好的压缩效果,但只有对高光谱图像进行无损压缩才可以在提高传输和储存效率、降低成本的同时,又保证了高光谱图像的质量。因此,在大多数情况下,对高光谱图像进行无损压缩是将其存储或传输之前必不可少的一步,高光谱图像的无损压缩技术也一直是当前国内外研究的热门领域。
高光谱图像具有两种不同的相关性,同一波段像素间的空间相关性和相邻波段像素间的谱间相关性。在高光谱图像中,谱间相关性远大于空间相关性,因此,在利用空间相关性的同时充分发掘高光谱图像中较强的谱间相关性是高光谱图像无损压缩算法取得良好压缩结果的关键。目前,常见的高光谱图像压缩算法根据其去除相关性方法的不同可分为3类:预测法、变换法和矢量量化法。其中,矢量量化法由于其庞大的算法复杂度对实际应用的制约,导致当前针对矢量量化法的高光谱图像压缩算法相对较少。变换法可使用较小的码字表示图像的大部分能量,方便了对细节分量的量化,因此多用于近无损压缩和有损压缩。预测法通过特定的预测准则对待测像素估值以得到预测误差的方法合理地利用了高光谱图像的空间相关性和谱间相关性,可以对高光谱图像取得良好的无损压缩效果的同时保持较低的算法复杂度,是近年来国内外研究的重点。
文献[1]提出的基于查找表(LUT)的预测压缩算法,将前一波段中与待测像素具有相同空间坐标的像素视为索引,通过在表中查找此索引得出最终预测结果。文献[2]对文献[1]中算法进行强化,该算法首先计算待测像素的LAIS(Locally Averaged Interband Scaling)参考值,通过在两个表内查找索引值得到两个预测结果,选择其中与LAIS参考值最接近的作为最终预测结果。文献[3]在完善文献[2]中LAIS参考值计算公式的同时,通过自适应量化因子的使用对索引值进行量化以达到减少表所占内存空间的目的。文献[4]提出了一种致力于机上压缩的FL(Fast Lossless)算法,该算法使用多个当前已知波段预测待测波段,并使用最小均方误差法(LMS)求解预测系数。文献[5]提出的IP3(Third-Order Interband Predictor)算法将其谱间预测的过程转化为维纳滤波的求解过程。文献[6]提出的RLS算法首次将递归最小二乘法引入到高光谱图像预测压缩领域。更多研究内容参见文献[7-20]。
预测压缩算法作为一种最经典且最成功的无损压缩算法之一,主要通过使用当前已知数据预测未知数据,已知数据的选取和预测系数的确定制约了预测压缩算法的准确度。而高光谱图像的图像纹理相对密集,对某一像素进行预测时,其近邻的已知像素往往都是不同地物的成像,选取属于不同地物的像素对待测像素进行预测极易造成预测失准,进而对算法的压缩性能造成损害。在高光谱图像中,同一地物在相同的光照强度、结构特征、覆盖植被种类等条件下具有相似的光谱信息,从而表现出较强的相似度,可划分到同一类中。对高光谱图像进行聚类处理,有助于去除其空间冗余,提高预测压缩算法的压缩性能。
本文提出了一种基于K-均值聚类和传统递归最小二乘法的高光谱图像无损压缩算法(C-CRLS)。首先,该算法以高光谱图像中的每条光谱矢量为样本进行K-均值聚类以提升同类光谱矢量间的相似度,去除空间冗余。然后,对每一聚类群分别使用传统递归最小二乘法预测以消除高光谱图像的谱间冗余。最后,对预测误差图像进行算术编码,完成压缩过程。该算法充分利用了高光谱图像的空间相关性和谱间相关性,在取得良好压缩结果的同时保持了相对较低的运算时间。
2 算法构造
为了充分利用高光谱图像光谱矢量间的冗余,提高算法的压缩比,本文将K-均值聚类算法与传统预测算法相结合得到新压缩算法。本文算法将高光谱图像的无损压缩过程分为3个步骤:聚类、预测和编码,图1展示了本文算法的流程图。
2.1 K-均值聚类
本文选用K-均值聚类算法[21]将高光谱图像中的每个光谱矢量(光谱矢量由高光谱图像各波段中同一空间坐标的像素构成)分配到与其距离最近的聚类群之中,整个聚类过程由以下5步组成:
(1)确定聚类群数目,本文通过仿真实验选择使用16个聚类群以获得最佳压缩效果。
(2)生成16个随机光谱矢量作为16个初始聚类群的中心点。
(3)将每个光谱矢量分配到最近距离的聚类群中,光谱矢量间的距离使用欧几里得距离,其表达式如式(1)所示,其中和分别表示一条光谱矢量,为光谱矢量的长度,即高光谱图像的波段数。
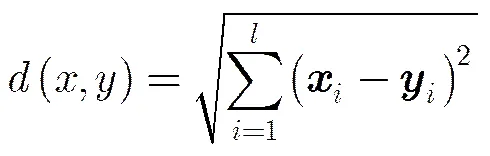
(4)对所有光谱矢量完成一次聚类后,重新计算每个新聚类群的中心点。
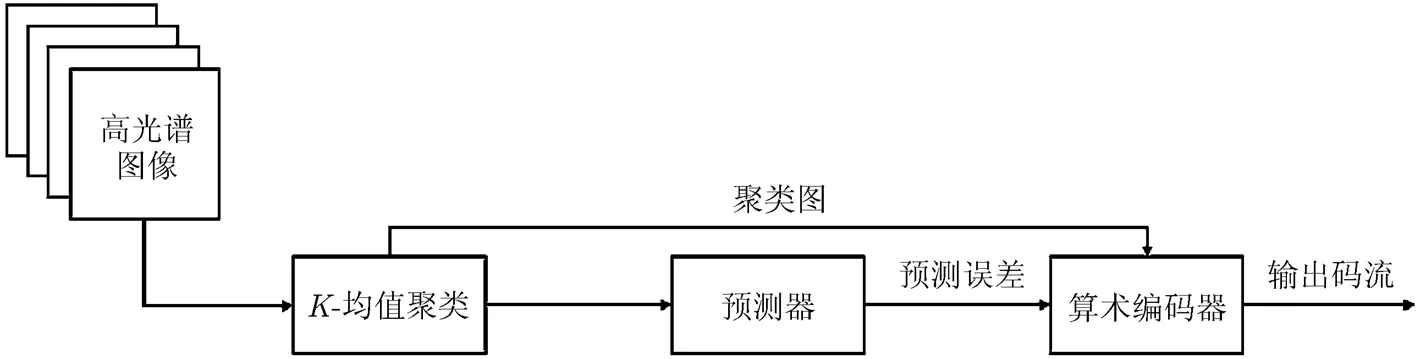
图1 本文算法流程图
(5)重复运行步骤(3)和步骤(4)直至算法收敛。
K-均值聚类算法通常需要使用不同的随机中心点多次进行初始化计算,然而以高光谱图像的光谱矢量作为数据集时,使用不同的随机中心点并不会影响压缩算法的最终压缩结果。因此,对于每一组高光谱图像,本文算法的K-均值聚类步骤只需运行一次,并未增加算法的整体复杂度。为了更直观地描述本文算法中的K-均值聚类过程,其算法流程图如图2所示。
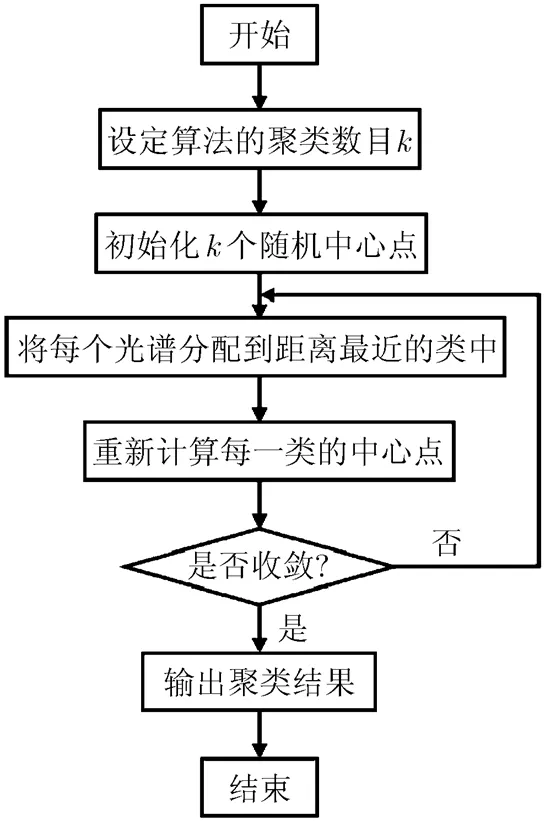
图2 K-均值聚类算法流程图
2.2传统递归最小二乘预测
本文算法对高光谱图像进行K-均值聚类后,分别对每一聚类群的重构图像使用传统递归最小二乘法[22]预测得到预测误差图像。在此阶段,本文将第波段中第行列的待测像素设为,当高光谱图像中像素按反向光栅扫描顺序排列时,本文也使用来表示第波段中的第个像素(其中为高光谱图像的宽度)。
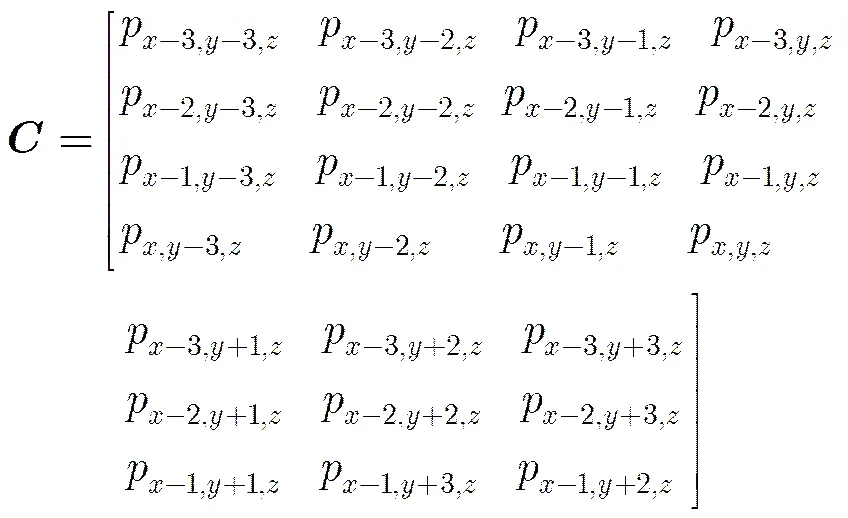
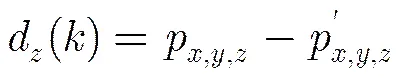
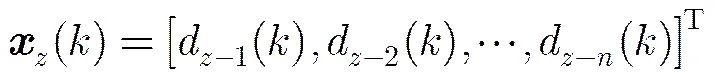
与输入向量相对应的系数向量定义为
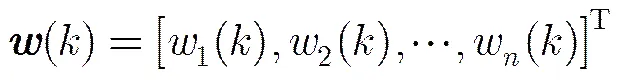
首先,对传统递归最小二乘法进行如下初始化,其中为单位矩阵,。
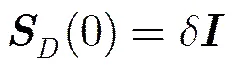
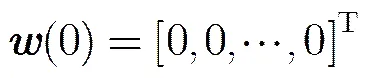
然后,使用递归最小二乘法预测待测像素,得出预测误差:
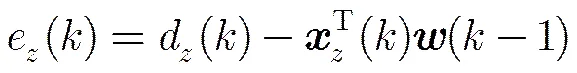
设:
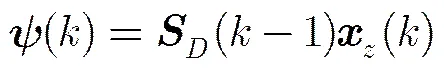
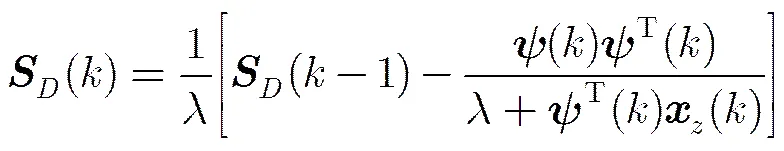
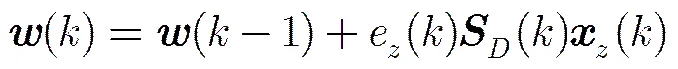
2.3算术编码
本文采用文献[23]中的算术编码器对预测步骤得到的误差图像进行编码压缩。由于文献[23]中算术编码器的输入只能为正整数序列,因此,本文算法在进行编码压缩之前,首先对预测误差图像进行转换,在转换序列中使用正整数表示预测误差图像中出现的第个新误差值。在预测误差图像全部转换完成后,使用算术编码器对转换序列和转换对应关系进行编码压缩,完成本文算法的全部压缩过程。
3 实验结果与讨论
为了验证本文算法的有效性,使用现有实验平台(Intel i7 3.80 GHz CPU/16GB RAM)对机载可见光/红外成像光谱仪(AVIRIS)于2006年获取的高光谱图像进行MATLAB仿真测试。AVIRIS 2006高光谱数据由5组16位校正图像、5组16位未校正图像和2组12位未校正图像组成,每组图像均包含224个光谱波段,图像宽度均为512列,其具体规格如表1所示。
3.1参数设定
仿真实验过程中相应的参数设定如下:
为上下文窗口大小,本文算法在=24(即上下文窗口中包含24个已知像素)时得到的压缩比较=4时高0.04,继续增大上下文窗口的尺寸无法获得更好的压缩结果,因此本文算法中上下文窗口的设定如式(2)所示。
3.2 压缩结果
表2比较了同样使用AVIRIS 2006高光谱数据作为实验图像的多种高光谱图像无损压缩算法的压缩结果,采用压缩比作为无损压缩算法性能的评价标准,其中包括JPEG-LS[7], LUT[1], LAIS-LUT[2], FL[4], IP3[5]和本文算法C-CRLS,对每组实验结果中的最高压缩比使用加粗表示。表2显示,本文算法对AVIRIS 2006高光谱数据中的16位校正图像、16位未校正图像和12位未校正图像分别取得了4.63倍、2.82倍和4.77倍的平均压缩比,高于所比较的其他高光谱图像无损压缩算法,并且,本文算法对12组高光谱数据中任意一组所取得的压缩结果也为最优。
表3对比了本文算法和同样基于递归最小二乘法的RLS算法[6]对相同实验图像进行压缩得到的压缩结果。表3显示,在以AVIRIS 2006高光谱数据中的16位校正图像、16位未校正图像和12位未校正图像分别作为实验图像时,本文算法得到的压缩比较RLS算法分别高出4%,2%和3%,对应提高的压缩比数值分别为0.17, 0.06和0.15。表3证明了与其他基于递归最小二乘法的高光谱图像无损压缩算法进行比较时,本文算法由于将K-均值聚类与预测算法结合,充分利用了高光谱图像的空间相关性和谱间相关性,因而在压缩性能的比较上更具优势。

表1 AVIRIS 2006高光谱图像规格
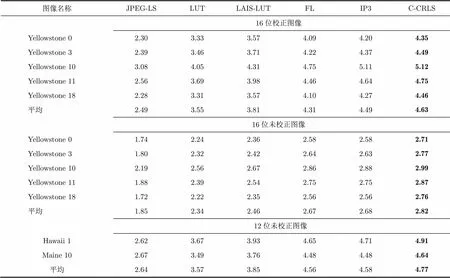
表2 多种算法对AVIRIS 2006高光谱图像的压缩结果比较
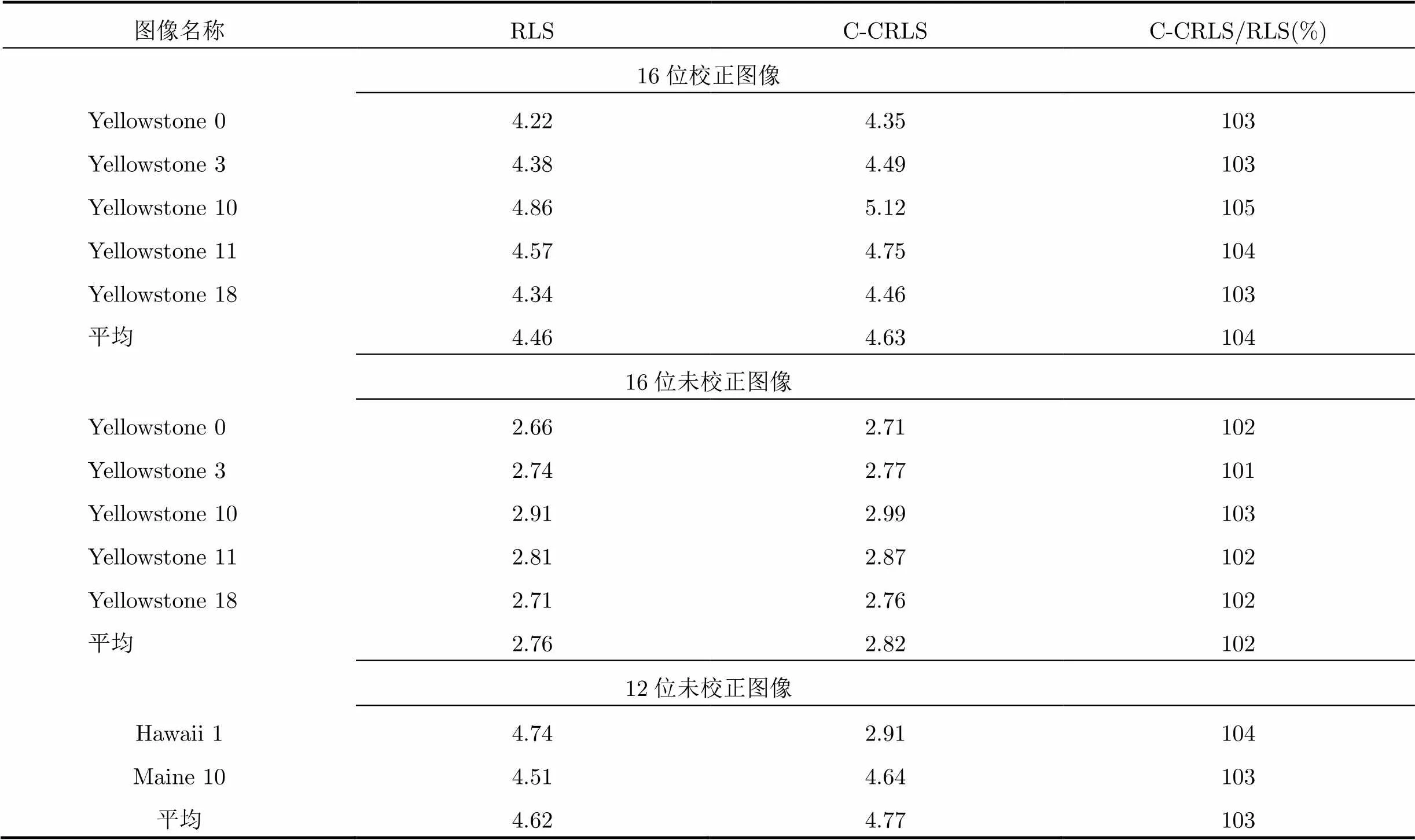
表3 本文算法和RLS算法对AVIRIS 2006高光谱图像的压缩结果对比
表4展示了本文算法对AVIRIS 2006高光谱图像进行压缩时的计算时间,其中cal和raw分别表示校正图像和未校正图像。对于本文算法,K-均值聚类对每场景图像的平均计算时间为12 s,算术编码对每场景图像的平均计算时间为71 s,传统递归最小二乘法预测对每波段图像的平均计算时间为3.7 s。本文算法的计算复杂度与RLS算法接近,从文献[6]中的数据对比可知,本文算法在运算时间上少于IP3算法,但多于LAIS-LUT和FL算法,这主要是由于本文算法在进行仿真实验时选取8个已知波段预测当前波段,而LAIS-LUT和FL算法分别只使用了1个和3个已知波段预测当前波段,减少了预测器的运算时间。
从上述对比中可以看出,JPEG-LS作为传统2维图像压缩算法,只利用了图像的空间相关性,取得了所比较算法中最差的压缩比,并不适用于高光谱图像。LUT算法和LAIS-LUT算法作为针对高光谱图像的无损压缩算法,使用一个已知波段预测当前波段,虽然具有运算时间短和算法复杂度低的特点,但同样只能获得差强人意的压缩比。FL算法和IP3算法着重利用高光谱图像的谱间相关性,使用多个已知波段预测当前波段,获得了更好的压缩比,但在运算时间上远高于LUT算法。而本文提出的C-CRLS算法,通过K-均值聚类和传统递归最小二乘预测分别去除了高光谱图像的空间冗余和光谱冗余,充分利用了高光谱图像的空间相关性和谱间相关性,取得了所对比算法中的最高压缩比,与此同时,本文算法在运算时间也优于IP3算法,证明了本文算法在取得高压缩性能的同时保持了相对较低的运算时间。
表4本文算法对AVIRIS 2006高光谱图像压缩的计算时间

图像名称计算时间(s) Yellowstone 0 cal 848 Yellowstone 3 cal 791 Yellowstone 10 cal1123 Yellowstone 11 cal1093 Yellowstone 18 cal 902 Yellowstone 0 raw 841 Yellowstone 3 raw 778 Yellowstone 10 raw1265 Yellowstone 11 raw1077 Yellowstone 18 raw 814 Hawaii 1 raw 702 Maine 10 raw 764 平均 917
4 结束语
为了充分提高高光谱图像无损压缩算法的压缩比,本文将图像聚类与预测压缩相结合,提出了基于K-均值聚类和传统递归最小二乘法的高光谱图像无损压缩算法。首先,对高光谱图像以光谱矢量为单位进行K-均值聚类以提升同类光谱矢量间的相似度。然后,对每一聚类群分别进行传统递归最小二乘预测。最后,对预测误差图像进行算术编码。对AVIRIS 2006高光谱数据进行仿真实验的实验结果表明,本文算法对16位校正图像、16位未校正图像和12位未校正图像分别取得了4.63倍,2.82倍和4.77倍的压缩比,优于同类型已报道的各种算法,同时,该算法具有相对较低的运算时间,证明了本文算法的有效性和实用性,为高光谱图像无损压缩提供了一种很好的解决方案。
[1] MIELIKAINEN J. Lossless compression of hyperspectral images using lookup tables[J]., 2006, 13(3): 157-160. doi: 10.1109/LSP.2005.862604.
[2] HUANG B and SRIRAJA Y. Lossless compression of hyperspectral imagery via lookup tables with predictor selection[C]. Conference on Image and Signal Processing for Remote Sensing XII, Stockholm, Sweden, 2006: 63650L.1- 63650L.8. doi: 10.1117/12.690659.
[3] MIELIKAINEN J and TOIVANEN P. Lossless compression of hyperspectral images using a quantized index to lookup tables[J]., 2008, 5(3): 474-478. doi: 10.1109/LGRS.2008.917598.
[4] KLIMESH K. Low-complexity adaptive lossless compression of hyperspectral imagery[C]. Conference on Satellite Data Compression, Communications, and Archiving II, San Diego, USA, 2006: 63000N-1-63000N-9. doi: 10.1117/12.682624.
[5] LIN Chengchen and HWANG Yintsung. An efficient lossless compression scheme for hyperspectral images using two-stage prediction[J]., 2010, 7(3): 558-562. doi: 10.1109/LGRS.2010.2041630.
[6] SONG Jinwei, ZHANG Zhongwei, and CHEN Xiaomin. Lossless compression of hyperspectral imagery via RLS filter[J]., 2013, 49(16): 992-993. doi: 10.1049/el.2013.1315.
[7] ABRARDO A, BARNI M, MAGLI E,. Error-resilient and low-complexity onboard lossless compression of hyperspectral images by means of distributed source coding[J]., 2010, 48(4): 1892-1904. doi: 10.1109/TGRS.2009.2033470.
[8] RIZZO F, CARPENTIERI B, MOTTA G,. Low- complexity lossless compression of hyperspectral imagery via linear prediction[J]., 2005, 12(2): 138-141. doi: 10.1109/LSP.2004.840907(410).
[9] MAGLI E. Multiband lossless compression of hyperspectral images[J]., 2009, 47(4): 1168-1178. doi: 10.1109/TGRS. 2008.2009316.
[10] MIELIKAINEN J and TOIVANEN P. Clustered DPCM for the lossless compression of hyperspectral images[J]., 2003, 41(12): 2943-2946. doi: 10.1109/TGRS.2003.820885.
[11] AIAZZI B, ALPARONE L, BARONTI S,. Crisp and fuzzy adaptive spectral predictions for lossless and near-lossless compression of hyperspectral imagery[J]., 2007, 4(4): 532-536. doi: 10.1109/LGRS.2007.900695.
[12] WU Jiaji, KONG Wanqiu, MIELIKAINEN J,. Lossless compression of hyperspectral imagery via clustered differential pulse code modulation with removal of local spectral outliers[J]., 2015, 22(12): 2194-2198. doi: 10.1109/LSP.2015.2443913.
[13] ULKU I and TOREYIN B U. Sparse representations for online-learning-based hyperspectral image compression[J]., 2015, 54(29): 8625-8631. doi: 10.1364/AO.54.008625.
[14] WANG Lei, BAI Jing, WU Jiaji,. Hyperspectral image compression based on lapped transform and Tucker decomposition[J].:, 2015, 36: 63-69. doi: 10.1016/j.image.2015.06.002.
[15] BEERTEN J, BLANES I, and SERRA-SAGRISTA J. A fully embedded two-stage coder for hyperspectral near-lossless compression[J]., 2015, 12(8): 1775-1779. doi: 10.1109/LGRS.2015.2425548.
[16] LEE C, YOUN S, JEONG T,. Hybrid compression of hyperspectral images based on PCA with pre-encoding discriminant information[J]., 2015, 12(7): 1491-1495. doi: 10.1109/LGRS. 2015.2409897.
[17] ZHAO Chunhui, LI Xiaohui, REN Jinchang,. A novel framework for object-based coding and compression of hyperspectral imagery[J]., 2015, 24(2): 300-305. doi: 10.1049/cje.2015.04.012.
[18] NIAN Yongjian, HE Mi, and WAN Jianwei. Lossless and near-lossless compression of hyperspectral images based on distributed source coding[J]., 2015, 28: 113-119. doi: 10.1016/j.jvcir.2014.06.008.
[19] ZHANG Lefei, ZHANG Liangpei, TAO Dacheng,. Compression of hyperspectral remote sensing images by tensor approach[J]., 2015, 147(1): 358-363. doi: 10.1016/j.neucom.2014.06.052.
[20] HUANG Bingchao, NIAN Yongjian, and WAN Jianwei. Distributed lossless compression algorithm for hyperspectral images based on classification[J]., 2015, 48(7): 528-535. doi: 10.1080/00387010.2014.920888.
[21] JAIN A K. Data clustering: 50 years beyond k-means[C]. 19th International Conference on Pattern Recognition, Tampa, USA, 2010: 651-666.
[22] DINIZ P S R. Adaptive Filtering: Algorithms and Practical Implementation[M]. New York, Springer, 2012: 195-227.
[23] MOFFAT A, NEAL R, and WITTEN I H. Arithmetic coding revisited[C]. Data Compression Conference, Snowbird, USA, 1995: 202-211.
Lossless Compression of Hyperspectral Images Using K-means Clustering and Conventional Recursive Least-squares Predictor
GAO Fang SUN Changjian SHAO Qinglong GUO Shuxu
(,,130012,)
To improve the compression ratio of lossless compression scheme based on prediction, a lossless compression scheme for hyperspectral images using K-means Clustering method and Conventional Recursive Least-Squares (C-CRLS) predictor is presented in this paper. The proposed scheme first clusters the spectral data into clusters according to their spectra using the famous K-means clustering method. Then, the proposed scheme calculates the preliminary estimates to form the input vector of the conventional recursive least-squares predictor. Finally, after prediction, the prediction residuals are sent to the arithmetic coder. Experiments on the Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) 2006 hyperspectral images show that the proposed scheme yields an average compression ratio of 4.63, 2.82, and 4.77 on the 16-bit calibrated images, the 16-bit uncalibrated images, and the 12-bit uncalibrated images, respectively. Experimental results demonstrate that the proposed scheme outperforms other current state-of-the-art schemes for hyperspectral images that have been previously reported.
Hyperspectral images; Image compression; Recursive least-squares; Clustering
TP751.2
A
1009-5896(2016)11-2709-06
10.11999/JEIT151439
2015-12-22;改回日期:2016-04-08;
2016-05-25
郭树旭 guosx@jlu.edu.cn
国家自然科学基金(41101419)
The National Natural Science Foundation of China (41101419)
高 放: 男,1987年生,博士生,研究方向为高光谱图像压缩.
孙长建: 男,1993年生,博士生,研究方向为数字图像处理.
邵庆龙: 男,1990年生,硕士生,研究方向为视频图像处理.
郭树旭: 男,1959年生,博士生导师,研究方向为数字图像处理与分析等.

